闭式叶轮五轴原位检测路径规划与实验验证

李文龙，王刚，尹周平

华中科技大学 数字制造装备与技术国家重点实验室，武汉 430074

闭式叶轮是核电、航空航天、能源动力、石油化工等领域的核心动力部件之一，其制造精度对整机服役性能至关重要。为满足服役要求，闭式叶轮设计为叶片、轮盘和轮毂一体化结构，加工及检测极为困难，主要体现在：①结构封闭，四面约束，流道狭长；②叶型复杂，叶片薄壁，扭曲度大；③材料难加工，刀具悬伸长，易产生切削振动和让刀变形，加工精度难以控制。现有方法大多采用离线三坐标检测，需将工件从机床搬运到特定测量室，劳动强度大，如CAP1400核电叶轮重达0.5 t，人工搬运极为困难。此外，二次装夹引起重定位误差，且由于定位基准的改变，无法对叶型超差区域进行补偿修复，加大了工件报废的可能性。

在工件无需二次装夹的前提下，使用数控机床集成的测头对叶轮叶片等复杂零件进行原位检测与加工误差分析已成为先进制造领域的研究前沿之一[1-3]。卢万崎等[4]研究了航空叶片等高测量法，用于叶片截面线拟合和叶型重构，其中原位检测技术可避免二次装夹定位和对刀引起的重定位误差和叶片变形，从而控制超差和产品报废率。Mears等[5]综述了机床集成测头在数控加工中的发展前景，着重指出原位检测技术在产品质量快速评估、生产周期控制、自适应加工方面的应用价值。文献[6-9]研究了复杂零件原位检测系统的误差分离与补偿方法，力图解决机床几何误差、测头半径误差、工件加工变形等对加工精度的影响。Huang等[10]采用原位检测技术研究了叶轮曲面测点与设计包络面的轮廓误差，用于侧铣加工过程让刀变形和误差补偿，实验中加工精度提升70%左右。Cho等[11]提出了一种基于网络互联的叶轮加工工序优化方法，采用专家系统减少与工艺规划有关的生产成本，其中原位检测技术可用于加工后叶片尺寸误差的快速评估。Liu等[12]对大型火箭发动机喷管加工过程中工件轮廓进行原位测量，并对当前加工状态下的曲面模型进行再设计，用于后续余量修正与补偿加工，可将加工精度控制在±0.1 mm范围内。

从几何原理上来说，五轴数控机床可加工的曲面特征一定可检测，所以闭式叶轮原位检测路径规划可以参考叶轮五轴加工方面的研究成果。Meng等[13]研究了4种刀具的曲面特征，并以叶片最大曲率值作为几何约束，生成无干涉五轴加工路径。王晶等[14]建立了五轴刀轴矢量整体优化新模型，可以改善机床运动性能。Chen[15]提出一种叶轮五轴侧铣加工刀轴方向优化方法，根据叶轮与刀具之间重叠区体积搜索最优刀轴方向，此外，文献[16-17]提出了类似的叶轮加工刀轴优化和工艺参数优化方法。Bi等[18-19]提出一种基于GPU硬件加速的刀轴可接近锥计算方法，用于避免加工过程中刀具与相邻叶片、轮盘和轮毂之间的干涉，并采用控制相邻刀轴夹角偏差的方法在可接近锥中搜索刀轴方向。可接近锥理论上可推广应用于五轴原位检测路径规划，但闭式叶轮结构封闭，流道狭长，叶片弯扭曲大，在测针/测柄不与轮盖、叶片、轮毂产生干涉的前提下，检测路径应尽可能光顺，避免机床急转急停以及旋转轴摆动过快存在的潜在干涉问题。

本文根据闭式叶轮曲面特征，定义了4种形式的可接近锥，构造了基于弹性势能最小化的五轴原位检测路径规划目标函数，应用前向欧拉差分法在定义的连续检测可接近锥中计算测轴方向，并通过某闭式叶轮原位检测实验进行验证。

1 叶轮可接近锥定义

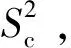
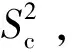
H∩So=Φ}

(1)

单点可接近锥的定义与五轴数控加工刀触点可接近锥定义类似，但待测点pi的可接近性需要保证从测量起点qi(qi=pi+lvi，其中l表示偏置常数)沿法矢方向vi无干涉接近点pi，即线段qipi上各点在测轴方向vic可接近,设pλ为线段qipi上的任意一点。

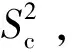
H∩So=Φ,∀pλ∈qipi}

(2)

线段qipi上存在无数个点，考虑到测点pi与起点qi距离很近，可取线段两端点的单点可接近锥的公共部分作为待测点pi处的可接近锥，即：

ACC(pi,vi,So)=ACS(pi,So)∩ACS(qi,So)

(3)

闭式叶轮流道狭长、扭曲度大，干涉严重，型面加工与测量时一般从进气端及出气端分别进行。如图2所示，设进气端流道截面的法矢方向为vin，出气端流道截面的法矢方向为vout。根据测轴方向vic与vin和vout夹角是否小于90°，可划分为进气端可接近锥和出气端可接近锥。

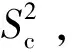
(4)

点pi的单点可接近锥为ACS(pi)，单点线段可接近锥为ACC(pi)，进气端可接近锥为ACCin(pi)，出气端可接近锥为ACCout(pi)。

根据约束关系，可将一条路径上的待测点划分为进气端待测点集和出气端待测点集：

(5)

式中：num(·)表示可接近锥中测轴方向矢量的数量。为保证相邻测点无干涉，进一步定义进气端连续检测可接近锥和出气端连续检测可接近锥。

进气端连续检测可接近锥：

(6)

出气端连续检测可接近锥：

(7)

式(6)和式(7)中EACC(pi)为单个测点pi的连续检测可接近锥；nin为进气端检测路径测点数。

连续检测可接近锥对当前待测点和其相邻点都可接近，给出了五轴原位检测测轴方向的可行域，即测头沿检测路径连续运动时与叶片曲面(接触点除外)和障碍物均不会发生干涉。

2 目标函数建模与测轴方向优化

2.1 构造目标函数

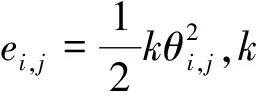
(8)

式中：θmax为角度阈值，保证检测路径光顺性，避免测轴方向变化过大引起机床急转急停。

如图3(b)所示，当所有弹簧受力平衡时，式(8)弹性势能最小，此时第i个测轴所受合力为

(9)

式中：fi,j表示第j个测轴相对第i个测轴的作用力，其模长和方向为

(10)

其中：di,j为矢量vjc-vic在对应高斯球面(测轴矢量vic)切平面上的投影。所以弹簧作用力为

fi,j=(kθi,j)di,j

(11)

注意，弹簧模型中首尾测轴受单向力作用，满足：

f1,0=fn,n+1=0

(12)

因此，式(8)中弹性势能最小化等价于：

(13)

式中：|F|为所有测轴所受合力的模长和。弹性系数k数值大小对参数计算结果无影响。

2.2 计算测轴方向

根据式(13)，为使弹簧达到受力平衡，考虑将每个待测点的测轴矢量vic沿合力fi方向转动一定角度，用于减小该点处所受合力。设待测点pi处测轴矢量vic为关于时间t的函数，则有：

(14)

式中：m为微分运算对应的合力系数。定义测轴方向初始值vic(0)=vic,0为与可接近锥EACC(pi)平均方向矢量夹角最小的矢量，其中平均方向矢量为

(15)

所以vic,0表示为

(16)

理论上当|fi|=0时，vic处于稳定状态，当整条路径合力|F|=0时，整条路径处于稳定状态，即路径光顺。下面可采用前向欧拉差分法计算测轴方向，设离散化时间间隔dt=Δt，在第u个迭代步骤，dvic=vic,u+1-vic,u,vic,u=vic(uΔt)，故：

(17)

注意，计算得到的vic,u+1必须在可接近锥EACC(pi)范围内，详细计算过程如图4所示，umax和e分别表示最大迭代次数和合力下降速度阈值。

3 闭式叶轮原位检测实验

3.1 检测路径生成与仿真实验

如图5所示，实验中采用某型号五叶闭式叶轮，叶轮外径为250 mm，高度为115 mm，叶片厚度为5 mm。每个叶片设计三条连续的检测路径，红色线表示待测点法矢方向，测量起点与待测点偏置常数l=10 mm，压力面和吸力面待测点数为35，前缘面待测点数为10。

由于闭式叶轮流道狭长，叶片弯扭曲，测头探针无法从流道一端完成整个叶片测量，实际加工或测量时均采用专用工装夹具对叶轮翻面装夹，因此规划检测路径时需根据待测点可接近锥分布对每条路径上的待测点集P分段。可接近锥的计算首先三角化高斯球面可获取离散参考方向(本文离散为1 280个)，采用借助于OpenGL的遮挡查询功能，在可接近锥的计算中考虑测杆大小，并由GPU实现并行计算，提高计算效率。详细计算过程可参考文献[3]。实验中，设定umax=200,Δt=0.1,m=0.1,e=10-5,θmax=5°。根据式(4)，计算每个待测点进气端可接近锥ACCin(pi)和出气端可接近锥ACCout(pi)，如图6所示。根据式(5)，将P划分为进气端点集Pin和出气端点集Pout，其中Pin包含37个待测点，Pout包含43个待测点。由于叶轮出气端后缘不需要检测，Pout以后缘为界，可划分为Pout1和Pout2两段，如图7所示。根据式(6)和式(7)，计算进气端连续检测可接近锥ACP(Pin)和出气端连续检测可接近锥ACP(Pout)。根据式(13)弹性势能最小化原理和式(17)参数求解方法，计算进气端待测点集Pin连续检测路径、出气端待测点集Pout1连续检测路径和出气端待测点集Pout2连续检测路径，如图8所示。

下面采用刀轴优化中常用的累积夹角最小化算法(角度法)[20]生成点集P的连续检测路径，计算所得测轴方向在可接近锥范围内，相邻测轴方向偏差不超过5°。计算结果如图9所示，可见角度法生成的连续检测路径在进气端前缘过渡处和出气端部分区域出现明显波动(绿色圈内)，即存在路径不光顺现象，将导致原位检测过程测轴急转急停。引起这一问题的主要原因是角度法目标函数以不产生干涉和控制相邻测轴方向偏差为主,未充分考虑连续检测路径的光顺性。

下面定义两种路径光顺性评价指标，对弹性势能法和角度法进行比较。角度增量指标：

Δθi=arccos(v(i+1)c·vic)-arccos(vic·v(i-1)c)

(18)

检测路径经后置处理后得到机床A、C转角，故也可根据A、C转角增量指标评价路径光顺性：

(19)

如图10所示为生成的进气端检测路径光顺性对比图。角度法生成的角度增量及A、C转角增量在路径起始区域及终止区域均存在较大波动，最大角度增量及A、C转角增量达到4°，可能导致机床急转急停，超出行程范围；而弹性势能法生成的角度增量及A、C转角增量控制在1°以下，不存在测轴方向突变，可避免机床急转急停问题。

3.2 原位检测与轮廓误差评估

如图11所示，原位检测实验在Mikron UCP800五轴加工中心进行，配备Renishaw OMP40测头(单点精度为0.001 mm，红宝石球直径为6 mm，探针长度为100 mm)，搭载Heidenhain iTNC530数控系统(A轴角度为-100°～+120°，C轴360°旋转)。将弹性势能法生成的检测路径在Delcam环境进行仿真与干涉检验，转化成加工中心可直接读取的.h文件，完成进气端和出气端原位检测。实验中，先完成进气端检测，通过工装翻面后再完成出气端检测，最终获得叶片曲面完整的检测误差数据。

三条检测路径对应的轮廓误差如图12所示，其中叶片从轮盖到轮毂共设置3行测点，分别对应图中三条曲线。每行共分布80个测点，包括吸力面待测点35个，前缘待测点10个，压力面待测点35个，其中前缘面属于高曲率区域，需要布置相对密集的测点以保证曲面特征检测信息尽可能完整。图12中正向误差值代表欠切，负向误差代表过切。由图可发现误差曲线大部分位于x轴以下，表示叶片大部分区域存在过切现象。除前缘处由于高曲率特征导致误差分布存在一定波动外，叶片曲面轮廓误差分布较为平稳，绝对值控制在0.1 mm范围内。引起加工误差的主要原因有：①刀具悬伸长，刚性差，加工过程中存在严重振动，同时闭式叶轮属于薄壁零件，结构刚性差，加工过程中工件易振动，这是引起过切的主因；②闭式叶轮加工及检测都需要进行翻面装夹，引入一定的装夹定位误差。

4 结 论

1) 根据闭式叶轮曲面结构，定义了单点可接近锥、单点线段可接近锥、进气端/出气端可接近锥、进气端/出气端连续检测可接近锥，为五轴原位检测刀轴方向优化提供可行域。

2) 构造基于弹性势能最小化的原位检测路径规划目标函数，并应用前向欧拉差分法在可接近锥中迭代计算测轴方向，生成无干涉且全局光顺的原位检测路径，可避免机床急转急停。

3) 将得到的检测路径导入Mikron五轴加工中心完成某型号闭式叶片原位检测，实验中角度增量及A、C转角增量不超过1°，验证了所提方法可保证全局光顺，具有重要应用价值。

参 考 文 献

[1] 蔺小军, 陈悦, 王志伟, 等. 面向自适应加工的精锻叶片前后缘模型重构[J]. 航空学报, 2015, 36(5): 1695-1703.

LIN X J, CHEN Y, WANG Z W, et al. Model restructuring about leading edge and trailing edge of precision forging blade for adaptive machining[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(5): 1695-1703 (in Chinese).

[2] 高健, 黄沛霖, 文章, 等. 复杂曲面零件加工精度原位检测系统的残余误差补偿[J]. 机械工程学报, 2016, 52(15): 139-146.

GAO J, HUANG P L, WEN Z, et al. Residual error compensation of in-situ inspection system for precision machining of complex components[J]. Journal of Mechanical Engineering, 2016, 52(15): 139-146 (in Chinese).

[3] LI W L, WANG G, ZHANG G, et al. A interference-free inspection path generation for impeller blades using an on-machine probe[J]. IEEE/ASME Transactions on Mechatronics, 2017, 22(3): 1218-1226.

[4] 卢万崎, 杨海成, 常智勇, 等. 一种叶片在机测量数据重构建模技术研究[J]. 航空制造技术, 2014(7): 84-87.

LU W Q, YANG H C, CHANG Z Y, et al. Blade reconstruction method in on-machine inspection[J]. Aeronautical Manufacturing Technology, 2014(7): 84-87 (in Chinese).

[5] MEARS L, ROTH J T, DJURDJANOVIC D, et al. Quality and inspection of machining operations: CMM integration to the machine tool[J]. ASME Journal of Manufacturing Science and Engineering, 2009, 131(5): 051006.

[6] BRANDY H T, DONMEZ MA, GILSINN D E. Methodology for compensating errors detected by process-intermittent inspection[M]. Gaithersburg: National Institute of Standards and Technology, 2001.

[7] CHO M W, KIM G H, SEO T I, et al. Integrated machining error compensation method using OMM data and modified PNN algorithm[J]. International Journal of Machine Tools and Manufacture, 2006, 46(12-13): 1417-1427.

[8] CHO M W, SEO T I. 2002 inspection planning strategy for the on-machine measurement process based on CAD/CAM/CAI integration[J]. International Journal of Advanced Manufacturing Technology, 2002, 19(8): 607-617.

[9] 陈岳坪, 高健, 邓海祥, 等. 复杂曲面的在线检测与加工误差补偿方法研究[J]. 机械工程学报, 2012, 48(23): 143-151.

CHEN Y P, GAO J, DENG H X, et al. On-line inspection and machining error compensation for complex surfaces[J]. Journal of Mechanical Engineering, 2012, 48(23): 143-151 (in Chinese).

[10] HUANG N D, BI Q Z, WANG Y H, et al. 5-axis adaptive flank milling of flexible thin-walled parts based on the on-machine measurement[J]. International Journal of Machine Tools and Manufacture, 2014, 84(6): 1-8.

[11] CHO M, KIM D, LEE C, et al. CBIMS: Case-based impeller machining strategy support system[J]. Robotics and Computer-Integrated Manufacturing, 2009, 25(6): 980-988.

[12] LIU H B, WANG Y Q, JIA Z Y, et al. Integration strategy of on-machine measurement (OMM) and numerical control (NC) machining for the large thin-walled parts with surface correlative constraint[J]. The International Journal of Advanced Manufacturing Technology, 2015, 80(9-12): 1721-1731.

[13] MENG F J, CHEN Z Y, XU R F, et al. Optimal barrel cutter selection for the CNC machining of blisk[J]. Computer-Aided Design, 2014, 53(5): 36-45.

[14] 王晶, 张定华, 罗明, 等. 复杂曲面零件五轴加工刀轴整体优化方法[J]. 航空学报, 2013, 34(6): 1452-1462.

WANG J, ZHANG D H, LUO M, et al. A global tool orientation optimization method for five-axis CNC machining of sculptured surfaces[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(6): 1452-1462 (in Chinese).

[15] CHEN K H. Investigation of tool orientation for milling blade of impeller in five-axis machining[J]. International Journal of Advanced Manufacturing Technology, 2011, 52(1-4): 235-244.

[16] CHU C H, HUANG W N, LI Y W. An integrated framework of tool path planning in 5-axis machining of centrifugal impeller with split blades[J]. Journal of Intelligent Manufacturing, 2012, 23(3): 687-698.

[17] WU B H, ZHANG D H, LUO M, et al. Collision and interference correction for impeller machining with non-orthogonal four-axis machine tool[J]. International Journal of Advanced Manufacturing Technology, 2013, 68(1-4): 693-700.

[18] BI Q Z, WANG Y H, DING H. A GPU-based algorithm for generating collision-free and orientation-smooth five-axis finishing tool paths of a ball-end cutter[J]. International Journal of Production Research, 2010, 48(4): 1105-1124.

[19] BI Q Z, WANG Y H, ZHU L M, et al. Wholly smoothing cutter orientations for five-axis NC machining based on cutter contact point mesh[J]. Science in China Series E: Technological Sciences, 2010, 53(5): 1294-1303.

[20] PLAKHOTNIK D, LAUWERS B. Graph-based optimization of five-axis machine tool movements by varying tool orientation[J]. International Journal of Advanced Manufacturing Technology, 2014, 74(1): 307-318.