感性耦合夹层等离子体隐身天线罩电磁散射分析

陈俊霖，徐浩军，魏小龙，陈增辉，吕晗阳

空军工程大学 航空航天工程学院，西安 710038

等离子体隐身技术是一种新概念的隐身技术，具有吸波频带宽、隐形效果好、不改变目标的外形、使用时间长、可以通过开关迅速地让等离子体产生和消失等优点[1-3]。在飞行器中天线罩是一种强散射源，电磁波可透过天线罩照射在雷达天线的复杂结构上形成很强的后向散射，感性耦合等离子体(ICP)可以在较低的射频功率和放电气压下获得稳定均匀、大面积高密度的等离子体，且装置结构简单，参数易于调节[4-6]，因此研究ICP在天线罩隐身技术上的应用具有较大的实际意义。

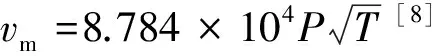
国内外相关学者在等离子体隐身效果的计算上做了大量工作，文献[9]采用Wenzel-Kramers-Brillouin (WKB)方法和分层近似研究了电磁波在非均匀等离子体中的传输特性，文献[10]采用Z变换时域有限差分 (ZT-FDTD) 方法研究了不同电子密度和碰撞频率的等离子体覆盖圆柱目标的雷达散射截面(Radar Cross Section，RCS)，文献[11]采用分段线性电流密度卷积时域有限差分(FDTD)方法分别计算了电磁波在磁化和非磁化、均匀和非均匀等离子体中的散射特性，并分析了在假设等离子体分布模型的覆盖下三维目标的RCS变化，文献[12]计算了薄层等离子体的衰减率，获得了大气等离子体在中高碰撞情况下的衰减系数。

前述的研究对等离子体参数空间分布普遍采用假设分布，如线性分布、二次分布、指数分布，直接利用假设分布构建WKB或时域有限差分模型计算等离子体的电磁散射特性，没有较好地解决等离子体放电与电磁散射特性计算的耦合问题，不能较好地反映实际分布的等离子体源对覆盖目标电磁散射特性的影响。

针对前述工作存在的不足，本文设计了一种石英夹层ICP天线罩模型，采用有限元和ZT-FDTD联合仿真的方法，建立二维等离子流体模型，得到了稳态下ICP中与电磁散射相关的电子密度空间分布，在此基础上建立ZT-FDTD模型，利用自编程序ZT-FDTD计算了不同放电条件下石英夹层ICP隐身天线罩的电磁散射特性，利用微波干涉法实验及XFDTD对软件计算方法进行了验证，该方法可为等离子体隐身实验的放电参数选择提供依据。

1 物理模型

本文研究的石英舱夹层ICP隐身天线罩模型如图1所示。天线罩外形是简单的旋转空心椭球体，外侧长半轴为10 cm，短半轴为8 cm，内侧长半轴为8 cm，短半轴为6 cm，中间夹层为等离子体产生区；在底部的石英窗下安装平面型线圈天线，该天线采用空心铜管绕制而成，外径为8 mm，内径为6 mm，匝数为一圈，直径为15 cm；为保证放电天线的长时间稳定工作，射频线圈连接自动循环水冷系统；射频电源为RSG-1000型，工作频率为13.56 MHz，额定输出功率为1 000 W，在功率源和射频线圈之间连接有自动射频阻抗匹配器以调节反射功率使其达到最小。在石英窗下侧对称安装2个直径为15 mm的石英接口，用于连接工质气体和真空泵。

工质气体设置为氩气，腔室内气压为2 Pa和20 Pa，放电功率为400～700 W，气温为常温293 K，根据天线罩模型设置放电特性的计算区域(图1)。

2 计算方法

2.1 ICP流体模型

在低温等离子体中，电子和电子能量的输运可以用一对扩散漂移方程来描述[13]，电子连续性方程为

(1)

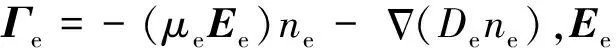
电子能量密度连续性方程为

(2)

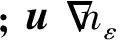
表1 模型涉及的化学反应Table 1 Chemical reaction of model

注：a为依赖于电子能量的分布函数。

重粒子的质量守恒采用混合平均方法进行计算，对于粒子k，满足：

(3)

式中：jk为扩散流矢量；Rk为粒子k的产生率；u此刻代表重粒子的平流流速；ρ为重粒子的混合密度；ωk为第k种粒子的质量分数。

腔体中的矢量磁势分布由频域的安培定律求解得到，即

(4)

式中：σ为电导率，σ=nee2/[me/(jω+vm)];me为电子质量，vm为碰撞频率;w为电磁角频率；ε0为真空中的介电常数；εr为相对介电常数；A为矢量磁势；μ0为真空中的磁导率；μr为相对磁导率；Je为线圈电流。

由法拉第定律，该磁场会在腔体中感应出电场：E=-jωA。

因此等离子体输入功率为

Pind=(1/2)real(E·J)

(5)

式中：J=σEe为腔体内的感应电流。电子和电子能量的边界条件设置不考虑电子的二次发射：

-n·Γe=(1/4)·veth·ne

(6)

-n·Γε=(5/3)·(veth·nε)/4

(7)

式中：n为边界表面的法线；veth为电子热运动速度。

由式(1)～式(7)可知该流体模型包含一组高度非线性且相互耦合的偏微分方程，用解析方法无法进行求解，本文利用软件COMSOL-Multiphysics中的等离子体模块对该流体模型进行求解。

COMSOL在求解过程中采用的是有限元方法。有限元法是基于变分原理和加权余量法的一种差分方法，其基本思想是将模型的求解域分割为有限多个互不重叠且在顶角处相互联接的小单元，这些小单元又称为基元，基元的角点称为节点，在每个基元内选择恰当的插值函数，将偏微分方程组中的所求变量分解为各节点上插值函数的线性组合，从而将非线性偏微分方程组近似为矩阵方程并进行求解。

网格是进行有限元计算的关键因素，对计算结果精度有着很大的影响。由于等离子体放电过程涉及的物化反应主要在放电腔室区域内进行，同时由于感应耦合放电具有趋肤效应等特点，在腔室壁面附近反应较为强烈。因此，本文采用了不同方式对各区域进行网格生成，如图2所示。对放电腔室区域进行加密处理生成高密度网格，并采用了边界层网格，其他区域网格较为稀疏，以减小计算量。

2.2 ZT-FDTD模型

电磁波在等离子体中的传播过程采用Maxwell方程表示为

(8)

(9)

(10)

式中：H为磁场矢量；Jd为极化电流密度wp为等离子特径频率。

本文采用ZT-FDTD方法作为等离子体与电磁波相互作用的计算分析方法。Z变换法可直接将电磁场方程在Z域内表征为离散差分方程，避免了积分项的引入，易于计算机编程且具有较高的精度[16]。等离子体在Z域上的本构关系为

D(z)=E(z)+S(z)

(11)

式中:D(z)为电位移矢量在Z域上的表达式，S(z)为辅助参量，表达式为

S(z)=z-1S(z)[1-exp(-vmΔt)]-

Δt[1-exp(-vmΔt)]

(12)

其中:含z-1和z-2的项分别代表辅助参量S(z)的前两个时间步的取值。ZT-FDTD对等离子体中电磁波的各场量的递推方法如式(13)～式(16)所示：

En=Dn-Sn

(13)

Sn=Sn-1[1-exp(-vmΔt)]-Sn-2·

(14)

(15)

(16)

该模型计算区域分为3个功能区：总场区、散射场区和完全匹配层(UPML)，如图3所示。在等离子体层下方有一块圆形铜板模拟天线，为降低建模难度，忽略了用于约束等离子体的石英结构，入射电磁波为覆盖主要雷达波频段的高斯脉冲，入射方向为天线罩轴线方向，极化方向为θθ极化。

计算中Yee元胞边长为3 mm，时间步长设为电磁波通过半个网格空间步长的时间。在等离子体区域迭代计算时，从流体模型计算得到的ωp的采样点数量是等离子体区域网格数量的4倍，每一个元胞中有9个采样点。介质界面处电磁参数的选取及完全匹配层的设置均参考文献[17-18]。

由上述ZT-FDTD方法计算得到近场后利用惠更斯远-近场变换公式可得到等离子体天线罩在某一方向的散射电场(设为Es(t))。经过傅里叶变换，可得其对应的频谱Es(f)为

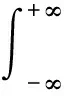
(17)

同样，经过傅里叶变换也可以得到入射波Ei(t)对应的频谱Ei(f)为

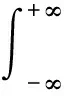
(18)

根据RCS的定义，可得到目标在某一方向的RCS随频率的变化为

(19)

式中:r为目标到雷达的矩离。

为验证该算法及开发程序的正确性和有效性，分别用自编的ZT-FDTD程序和XFDTD软件计算无等离子体及等离子体均匀分布且电子密度为1×1017m-3，气压为2 Pa时天线罩的后向RCS，结果数据对比如图4所示。

可以看出，在有/无等离子体的条件下，采用ZT-FDTD得到的计算结果与XFDTD软件结果都能较好地吻合，在某些频段存在一定的差异，这主要是因为网格的剖分密度不同造成的。

3 计算结果分析

3.1 ICP电子密度空间分布

运用COMSOL软件中的等离子体模块对上述流体模型进行运算，图5(a)和图5(b)为在放电功率PD为400 W，气压为2 Pa和20 Pa时由流体模型得到的在放电处于稳态时的电子密度分布,横坐标R为柱坐标的径向坐标。可以看出，气压为2 Pa时其夹层区域电子密度沿腔体分布较均匀，这是因为此时电子的平均自由程(约为2.2 cm)和放电的夹层区域的尺寸差不多，此时虽然电源能量主要注入到射频电磁场趋肤层内，但由于电离过程的变化尺度和电子平均自由程相近使得电子能扩散至整个腔体，从而使夹层内电子密度的空间分布仍然比较均匀[19]。而在气压为20 Pa时电子密度明显提高，同时沿着腔体分布具有较大梯度，出现这种现象的原因是气压为20 Pa时电子平均自由程相比于2 Pa时下降了10倍，远小于夹层区域尺寸，碰撞电离主要被限制在射频电磁场的趋肤层内，导致ne在腔体夹层区域中的分布出现较大梯度，同时气压升高导致碰撞频率有效提高，使电子密度有效增强[20]。

为验证流体模型的准确性，基于图1的模型开展放电实验，运用微波干涉法对等离子体电子密度进行诊断，其实验系统装置如图7所示，该系统由矢量网络分析仪和喇叭天线组成，在石英腔底面放置铝板，由矢量网络分析仪记录微波信号通过等离子体后的相移Δφ，在铝板下方放置吸波材料。

微波探测路径上等离子体的平均电子密度为[21]

(20)

图8为不同放电条件下实验结果与计算结果的对比。可以看出实验结果与仿真结果符合较好，微波干涉法诊断结果略低于流体模型结果，这主要是由于在流体模型中没有考虑功率损失、容性分量等对的影响，同时也可以看出随着功率提高，模型的误差减小，说明在低功率情况下，容性分量在总耦合功率中占比较高。

3.2 等离子体天线罩隐身效果分析

图9给出放电气压为2 Pa，不同放电功率PD下和无等离子体时天线罩的后向RCS对比。加上ICP后，在低频段(0～0.7 GHz)，RCS变化很小，这是由于此时电磁波波长远大于天线罩尺寸，天线罩处在电磁散射的瑞利区，RCS主要由天线罩体积决定；而在2 GHz以上较宽的频率范围内加上ICP后可使天线罩的RCS明显下降。

由于气压在2 Pa时碰撞频率处于106Hz量级，而对应的频率处于1 GHz量级：ωp≪vm，碰撞衰减较弱，因此在2～20 GHz频段内，对RCS的平均衰减较低，但在接近等离子体频率的局部窄带衰减较高，衰减的峰值随着功率的增大向高频方向移动，这是因为当入射电磁波的频率接近时，会产生较强的共振衰减作用，衰减峰值区出现在4.2～5.1 GHz频带内，功率增加衰减峰值不一定增加。

图10为放电气压为20 Pa，不同放电功率PD下和无等离子体时天线罩的后向RCS对比，相比于气压为2 Pa，此时RCS衰减超过10 dBsm的频带更宽，同时衰减效果也有所增加，这是由于此时电子密度分布不均匀使得等离子体振荡频率在空间有较大梯度，因此在更宽的频段范围均能对电磁波造成共振衰减，同时，等离子体碰撞频率提高了10倍，使得碰撞衰减增强，从而有效增强衰减效果。主衰减频带随着功率的升高向高频方向移动，同时曲线的波动特性加强，即出现“振铃”现象[22]，这是由于ωp空间梯度的扩大加剧了散射波的繁杂性，导致RCS的波动特性加强。

4 结 论

1) 感性耦合等离子体可产生较高电子密度的等离子体，能有效实现RCS的减缩。

2) 气压为2 Pa时，碰撞衰减较弱，等离子体密度分布较均匀，衰减带宽集中在共振频率附近，功率增加会使衰减峰值向高频方向移动。

3) 气压为20 Pa时，碰撞衰减增强，且等离子体密度分布有较大梯度，衰减带宽有效增加，RCS曲线的波动特性加强。

参 考 文 献

[1] SINGH A, DESTLER W W, CATRAVAS P. Experimental study of interaction of microwave with a nonmagnetized pulsed-plasma column[J]. Journal of Applied Physics, 1992, 72(5): 1707-1719.

[2] DAVID H L. Plasma stealth[J]. New Scientist, 2000, 168(2264): 60.

[3] 白希尧, 张芝涛, 杨波, 等. 用于飞行器的强电离放电非平衡等离子体隐身方法研究[J]. 航空学报, 2004, 25(1): 52-54.

BAI X Y, ZHANG Z T, YANG B, et al. Study on the method of non-Equiblium plasma stealth by using strong ionization discharge[J]. Acta Aeronautica et Astronautica Sinica, 2004, 25(1): 52-54 (in Chinese).

[4] 赵文锋, 杨洲, 王卫星, 等. 基于CFDRC 的感应耦合等离子体离子数密度空间分布仿真[J]. 高电压技术, 2014,40(1): 206-211.

ZHAO W F, YANG Z, WANG W X, et al. Simulation on the spatial distribution of ICP ion number density based on CFDRC[J]. High Voltage Engineering, 2014, 40(1): 206-211 (in Chinese).

[5] NAKAGAWA H, MORISHITA S, NODA S, et al. Characterization of 100 MHz inductively coupled plasma ICP by comparison with 13.56 MHz ICP[J]. Journal of Vacuum Science & Technology A, 1999, 17(4): 1514-1519.

[6] MAHONEY L J, WENDT A E, BARRIROS E, et al. Electron-density and energy distributions in a planar inductively coupled discharge[J]. Journal of Applied Physics, 1994, 76: 2041-2047.

[7] 常雨, 陈伟芳, 孙明波, 等. 等离子体涡电磁散射特性及隐身性能[J]. 航空学报, 2008, 29(2): 304-308.

CHANG Y, CHEN W F , SUN M B, et al. Scattering and stealth of plasma vortex[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(2): 304-308 (in Chinese).

[8] 陈楠. 基于FDTD等离子体天线隐身及辐射性能研究[D]. 衡阳： 南华大学， 2010： 31-32.

CHEN N. Research on plasma antenna stealth and radiation performance based on FDTD method[D]. Hengyang: University of South China, 2010： 31-32 (in Chinese).

[9] BRUSKI L G, MASE A, TAMANO T, et al. Application of one-dimensional Wentzel-Kramers-Brillouin approximation in microwave reflectometry of plasma density profiles[J]. Review of Scientific Instruments, 1998, 65(5): 2184-2185.

[10] 刘少斌, 莫锦军, 袁乃昌. 非磁化等离子体密度与目标雷达隐身的关系[J]. 电波科学学报, 2003, 18(1): 57-61.

LIU S B, MO J J, YUAN N C. Research on the relation between the unmagnetized plasma density and the stealth of target[J]. Chinese Journal of Radio Science, 2003, 18(1): 57-61 (in Chinese).

[11] SULLIVAN D M. Frequency-dependent FDTD method using Z transforms[J]. IEEE Transactions on Antennas Propagation, 1992, 40(10): 1223-1230.

[12] LIU M, HU X, JIANG Z. Attenuation of wave in a thin plasma layer by finite-difference time-domain analysis[J]. Journal of Applied Physics, 2007, 101(5): 1661.

[13] 张文茹. 氩气放电的流体力学模拟及其COMSOL软件的验证[D]. 大连： 大连理工大学， 2013: 8-9.

ZHANG W R . The fluid simulation of argon discharge and its verification with COMSOL software[D]. Dalian: Dalian University of Technology, 2013: 8-9 (in Chinese).

[14] ANGEL O B, CORNELIA B. Fast and reliable simulations of argon inductively coupled plasma using COMSOL[J]. Vacuum, 2015, 116: 65-72.

[15] MORAVEJ M. Properties of an atmospheric pressure radio-frequency argon and nitrogen plasma[J]. Plasma Sources Science & Technology, 2006, 15(2): 204-210.

[16] 杨利霞, 许红蕾, 孙栋, 等. 双各向异性色散介质电磁波传播Z-时域有限差分分析[J]. 电波科学学报, 2015, 30(3): 423-428.

YANG L X, XU H L, SUN D, et al. Electromagnetic scattering by bianisotropic dispersive media by using Z-FDTD method[J]. Chinese Journal of Radio Science, 2015, 30(3): 423-428 (in Chinese).

[17] ELSHERBENI A Z, DEMIR V. The finite-difference time-domain method for electromagnetics with MATLAB simulation[M]. North Carolina: SciTech publishing Inc., 2006: 31-40.

[18] 葛德彪, 闫玉波. 电磁波时域有限差分方法[M]. 3版. 西安: 西安电子科技大学出版社, 2011: 83-96.

GE D B, YAN Y B. Finite-difference time-domain method for electromagnetic waves[M]. 3rd ed. Xi’an: Xidian University Press, 2011: 83-96 (in Chinese).

[19] BRAINTHWAITE N St J. Introduction to gas discharge[J]. Plasma Sources Science and Technology, 2000, 9(4): 517-527.

[20] LICHTENBERG A J, LIEBERMAN M A. Principles of plasma discharges and materials processing[M]. New York: John Wiley & Sons, Inc., 2005: 304-305.

[21] 杜寅昌, 曹金祥, 汪建, 等. 射频电感耦合夹层等离子体中的模式转换[J]. 物理学报. 2012, 6(19): 337-342.

DU Y C, CAO J X, WANG J, et al. Mode transition of inductively coupled plasma in interlayer chamber[J]. Acta Physica Sinica, 2012, 6(19): 337-342 (in Chinese).

[22] LIU S B, YUAN N C, MO J J. A novel FDTD formulation for dispersive media[J]. IEEE Microwave and Wireless Compoents Letters, 2003, 13(5): 187-189.