GNSS导航系统快速选星算法研究

王永梅

（1.中国科学院国家空间科学中心北京100190；2.中国科学院大学北京100190）

全球导航卫星系统（GNSS）具有实时连续、全覆盖、全天候的精密导航定位能力，被广泛运用于测量、授时、定位等领域，全球4大定位系统包括：GPS、GLONASS、北斗、伽利略。

随着技术的发展，GNSS系统越来越成熟，有着无限的导航定位活力和潜能。但随着可见星数目的增加，以及用户对接收机处理数据的能力和速度提出的要求越来越高，无论是对单星导航系统还是多星导航系统，改进的选星算法成为了定位技术的重要问题。文中调研了传统的选星算法，整合了改良的几种算法，并对该方法的精度、误差、实时性进行了剖析。

1 GDOP值介绍

卫星导航的定义中，导航定位误差的标准偏差σG可以用以下的式子表示：

卫星导航系统的定位精度由GDOP与σUERE两方面决定，σUERE表示伪距测量值的标准偏差，GDOP表示σG和σUERE之间的比例关系。

从上式中不难发现，GDOP值是影响卫星定位精度的一个关键参数，在伪距测量值的标准偏差确定的情况下，定位系统的精度和GDOP值呈反比例关系，简言之，导航系统的精度随GDOP值的减小而提高。因此最小的GDOP值成为GNSS导航系统追求的优化指标。GDOP值的计算公式如下：

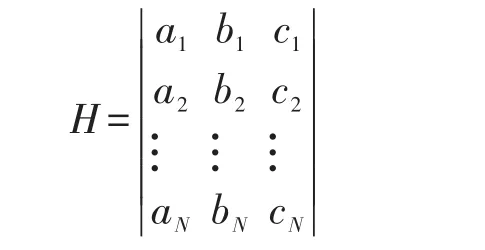
上式a，b，c是方向余弦，N是可视星颗数。观测矩阵如下：

1）单卫星导航系统

其中脚标1，2…N表示N颗卫星。

2）多卫星导航系统

GDOP可以用以下式子表示：

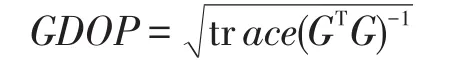
式中trace是求迹运算。

2 常用的选星算法

2.1 最佳几何误差因子法

最佳几何误差因子法是对所有可见的卫星，利用GDOP值的求解公式，得到最小的GDOP值的方法。假设某一时刻的可视星数为N，在N颗星中选m颗星用于导航，其中m＜N，共有种组合数。利用遍历的方法，依次对每种组合数的几何精度因子值求解，选几何精度因子值最小的可视星组合进行导航。该方法简单可靠，有很好的定位精度，但在遍历计算中，需要进行次矩阵相乘和求逆的运算，运算复杂，用时长，尤其在可视星数目较多的时候实时性差。

2.2 最大四面体体积法

最大四面体体积法是选择由可视星和接收机形成的多面体中，体积V最大的组合来进行导航的方法，因为V越大，GDOP值越小，因此能提高导航能力。以4颗星的组合为例，在可视星中选则4颗和接收机组成四面体，分别求出所有组合的V，选V最大的可视星组合用于导航。因为该方法遍历了所有4颗星的卫星组合，计算了每种组合中四面体的体积，所以计算量大，耗时久，实时性差。

2.3 最大行列式法

最大行列式法是选择由方向余弦组成的矩阵行列式值最大时所对应的卫星组合。由几何精度因子值的计算式发现，几何精度因子值和行列式绝对值之间成反比关系，几何精度因子值随行列式绝对值的增加而减小。由于利用最大行列式法可减少因为GDOP值计算带来的次矩阵相乘和求逆运算，因此降低了计算任务，并且耗时更短。

3 改进的选星算法

上文介绍的几种常用的选星算法计算量大，搜索时间长，无法满足用户对快速定位、高实时性等方面的需求。因此，本文整合了3种改进的GNSS导航系统选星算法，分析了每个改进算法的计算量、误差和耗时性，对优化的选星算法应用于接收机进行实时定位，具有重要的参考意义和价值。

3.1 基于仰角、方位角的选星算法

在可视星中居于顶位的星仰角越大，且居于底部仰角较小的可视星的方位角相差越平均，所得的几何精度因子值会越小。基于仰角、方位角的选星方法[1]具体步骤如下：

1）根据导航系统，从可见星中确定用于导航定位的卫星数a+b（a为顶座星数目，b为底座星数目）；

2）a颗居于顶部的可视星，其选取要求是选则仰角最大的星，再选取仰角最小的星为第1颗居于底部的星；

3）对剩下的可视卫星的选取原则是，选则方位角与标准角接近，高度角也尽量小的卫星，标准角的选取原则是依次在第一颗底部卫星的方位角上加上的角度。

当方位角与标准角差值小与高度角尽量小的要求发生冲突时，应以哪个标准进行选择，已有学者提出解决方案，第一，通过引入Bi作为标准来进行选择，第二，利用模糊评判的思想提出了模糊选星算法进行选择。

仰角、方位角的算法中，最优的顶座星和底座星的选取方法：当选5颗可视星定位时，取2颗为顶座星，3颗为底座星，顶座星选择仰角最大的和次大的，底座星选取仰角最小的为第3颗，选与第3颗可视星方位角差 120°、240°，且仰角最小的为第4、5颗。当选6颗可视星进行定位时，取2颗为顶座星，4颗为底座星，顶座星选仰角最大的和次大的，底座星选仰角最小的为第3颗，选与第3颗可视星方位角差90°、180°、270°，且仰角最小的为第4、5、6颗。

该快速选星方法中，用可视星的仰角α和方位角β来定义定位方程系数矩阵G，G又可分为单星导航系统和多星导航系统。

1）单卫星导航系统公式

2）双卫星导航系统公式

以北斗和GPS组合导航系统为例：

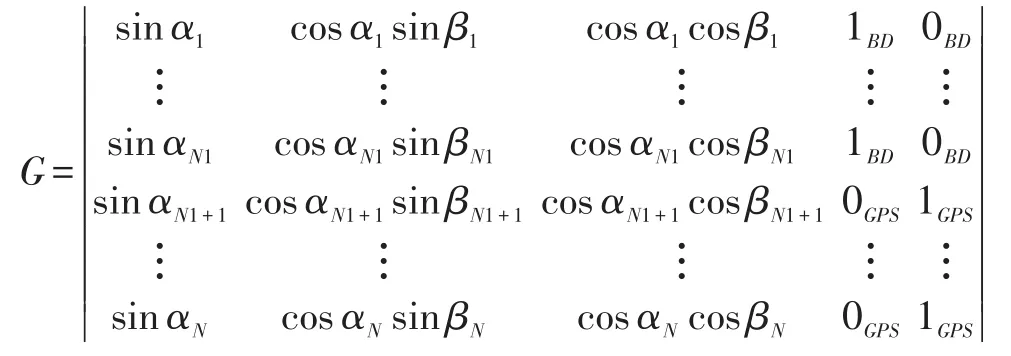
利用该选星算法和最佳几何精度因子法，可获得不同的GDOP值，进行比较，可得，6星的GDOP值偏差小于1.98%，精度很高。

表1 算法结果比较

250分钟总时间内，对每分钟的卫星数据进行分析，得到的GDOP差值如图1，可见该方法和最佳GDOP值方法对比，GDOP差值全部小于0.6，差小于0.2的时间段高达80%，表明仰角、方位角的算法有较好的定位能力。

图1 GDOP差值

3.2 改进的最大四面体体积法

最大四面体体积法：选出由接收机和可视星构成的四面体中，体积V最大的可视星进行定位。但由于GPS、GLONASS、北斗、伽利略系统的卫星轨道高度不同，计算出的体积值大也不能代表定位精度高，因此需要改进最大四面体体积算法。具体做法是：第一：选择一颗仰角最大的可视星，第二：在其余的可视星中用最大体积法选4颗可视星，第三：可视星到接收机的长度单位化，使高度统一，避免体积偏差。以接收机为原点，把接收机与4颗卫星的连线组成的矢量单位化，表示为e1、e2、e3、e4，把不同高度的轨道统一为相同的高度，把由这些矢量的末端形成的体积记作V，有如下关系式：

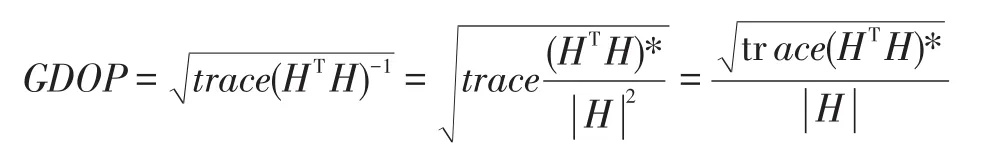
上式中，(HTH)*为HTH的伴随矩阵，trace（）是矩阵的求迹运算，假如设，那么。V和H之间关系是，，则GDOP值可表示为。由公式可知，利用体积V和行列式的关系，可以取消矩阵的复杂求逆运算。

如图2所示，该算法和最小几何精度因子法及最大行列式法的计算值相比，求出的GDOP值在允许的误差之内[2]。从图3可知改进的最大四面体体积法的运行时间最短，提高了实时性。

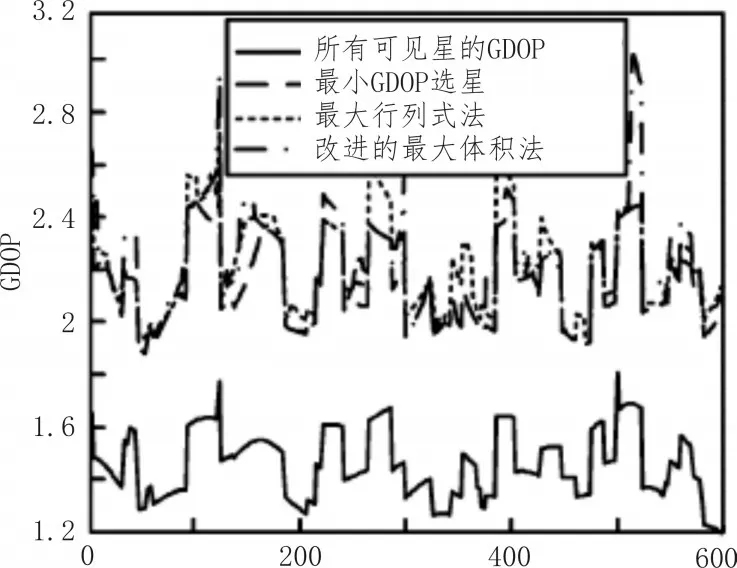
图2 GDOP值比较图

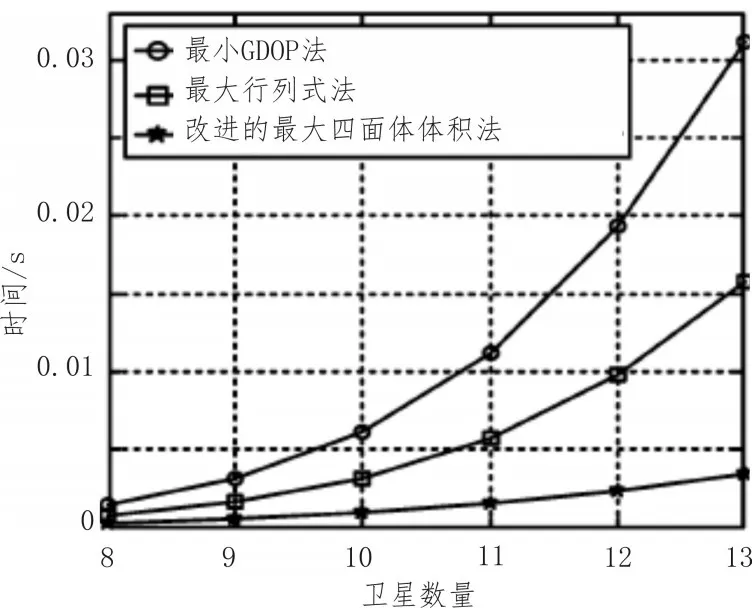
图3 运行时间汇总图

3.3 改进的行列式算法

以GPS卫星系统为例，一般采用最小二乘法来获得位置，但是算法的精度依赖于伪距的测量精度，实际定位过程中是假设伪距测量的精度相同，研究发现，观测卫星的仰角越大，伪距观测量越小。为了解决这个问题，引入加权最小二乘法[3]。将伪距方程变化为矩阵方程：

r是卫星与信号接收器之间的伪距值，Δxu、Δyu、Δzu表示信号接收器真实值与估计值在X、Y、Z方向上的偏差，c是光速，Δtu是卫星时间偏差，a、b、c是X、Y、Z方向上的余弦值。上式可以简化为：

σ代表GPS可视星伪距勘测误差的方差，加权几何精度因子为：

加权几何精度因子主要与加权行列式WG有关，仿真得出GDOPWG随着加权行列式WG的增大而减小。改良的方法为，第一，计算GPS系统中加权行列式的绝对值最大的m组星，第二，求解这m组可视星所对应的加权GDOPWG值，第三，选则最小的GDOPWG相对应的卫星来定位。由此方法计算得出的精度如图4所示，其中横坐标相对比值为(GDOPWG-GDOPmin)/GDOPmin，纵坐标是 (GDOPWG-GDOPmin)/GDOPmin值小于某个数时，组合卫星所占的百分比。由图知，当采用十五组GPS卫星时，该改进方法与最小几何精度因子算法的差值小于0.1，所占比例高达80%，差值小于0.15的比例高达85%，充分说明改进的加权行列式算法精度高，偏差小。

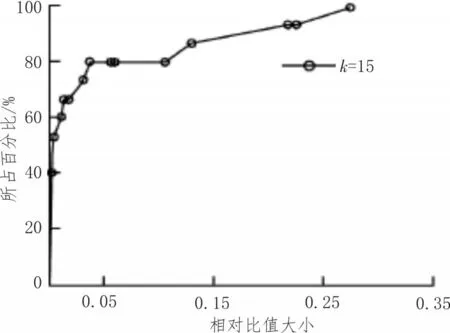
图4 定位精度结果图

在耗时方面，由图5的仿真结果可知，改进算法所需时间平均在15 ms，最小几何精度因子算法所需时间在32 ms，充分表明该改进算法比最小GDOP值算法所需时长少，耗时性更佳，时间上的优越性在组合数越多时越能更好体现。

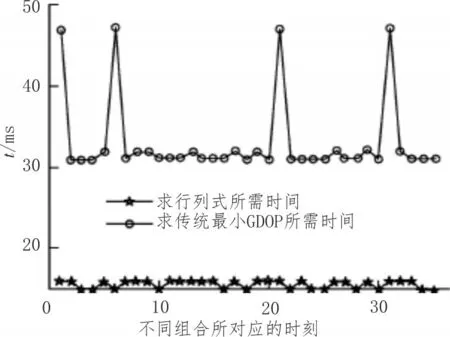
图5 改进行列式算法与最小GDOP值的耗时情况

4 结 论

通过总结GNSS系统中传统的选星方法与改进的几种选星方法，得出以下结论：基于仰角、方位角的选星方法精度较高，6星的GDOP值与传统最小几何精度因子法相比偏差小于1.98%，且计算方法简单，计算量小，实时性好，是一种高效的快速选星算法；改进的体积法、改进的行列式算法精度在允许范围之内，运算量得到明显改善，耗时性得到提高。可以得出这3种改进的选星算法能很好应用于接收机进行快速选星，实现实时性定位。

参考文献：

[1]赵新，张建军，朱立东.北斗导航系统的快速选星算法研究［J］.空间电子技术，2012（2）：4-9.

[2]江钰凯.GNSS卫星导航精度与选星算法研究[J].无线电工程，2014（7）：54-65.

[3]田安红，付承彪，董德春.一种改进的选星算法在GPS定位系统中的应用，海军工程大学学报，2014（2）：45-48.

[4]邓刚.基于卫星仰角和GDOP的GPS选星算法[J].数字通信，2010，2（3）:47-50.

[5]黄继拯，刘红，赵艳.GPS/北斗的组合选星算法研究[J].舰船电子工程，2011，31（8）:81-83.

[6]霍航宇，张晓林.组合卫星导航系统的快速选星方法[J].北京航空航天大学学报，2015，41（2）:273-276.

[7]许承东，李怀建，张鹏飞.GNSS数学仿真原理及系统实现[M].北京:中国宇航出版社，2011.

[8]吴甜甜，张云，刘永明，等.北斗/GPS组合定位方法[J].遥感学报，2014（5）:1087-1097.

[9]任磊，王雪梅.高动态GPS/INS组合导航中一种新的选星算法[J].计算机测量与控制，2011，19（12）：3096-3010.

[10]纪龙蛰，单庆晓.GNSS全球卫星导航系统发展概况及最新进展[J].全球定位系统，2012，5（37）：56-61.

[11]杨元喜.北斗卫星导航系统的进展、贡献与挑战[J].测绘学报，2010，39（1）:1-6.

[12]詹鹏宇.基于GNSS的高轨卫星定位技术研究[D].南京:南京航空航天大学，2012.

[13]陈灿辉，张晓林.一种新的卫星导航系统快速选星方法[J].电子学报，2010，38（12）:2887-2891.

[14]曾庆化，刘建业，胡倩倩，等.北斗系统及GNSS多星座组合导航性能研究[J].全球定位系统，2011，1（1）：52-57.

[15]高成发，胡伍生.卫星导航定位原理与应用[M].北京:人民交通出版社，2011.

[16]韩天祥.GNSS多系统选星策略的研究[D].上海：上海交通大学，2014.

[17]唐洪军.SOP算法在抗干扰卫星导航天线中的应用[J].电子科技，2017（5）:120-123.

[18]蔡明圭，谢军，王岗.卫星导航系统中恒包络复用算法的研究[J].电子设计工程，2016（7）:70-72.

[19]洪冰清，覃新贤，陈海强.多系统兼容卫星导航接收机关键技术概述[J].电子科技，2017（6）：150-153.