具变号非线性项三阶多点边值问题的正解与多个正解

沈春芳,杨 刘,解大鹏

(合肥师范学院数学系,安徽合肥 230601)

1　引言

本文研究如下三阶常微分方程m点边值问题

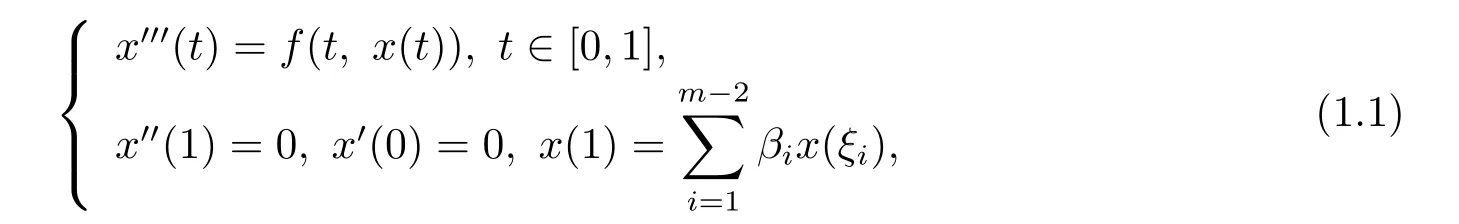
(H)f∈C([0,1]×[0,+∞),(−∞,+∞)),f(t,0)≥0,t∈[0,1]且不恒为0.

三阶常微分方程边值问题广泛出现在流体力学、天文学、弹性振动等问题中[1],对相关问题正解的研究近年来受到人们广泛的关注.利用非线性泛函分析方法,对三阶微分方程边值问题正解与多个正解的存在性的研究取得了丰富的结果,可参考文献[2–12].Anderson[2]研究如下三阶三点边值问题

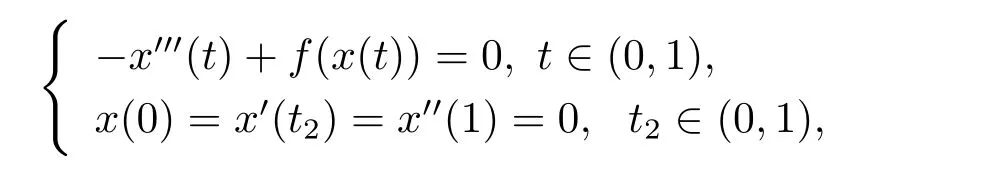
其中f:R→ [0,+∞)连续,1/2≤t2＜1,文中建立了问题至少三个正解的存在性结果.Palamides[3]利用范数形式的锥拉伸锥压缩不动点定理,证明了三阶三点边值问题

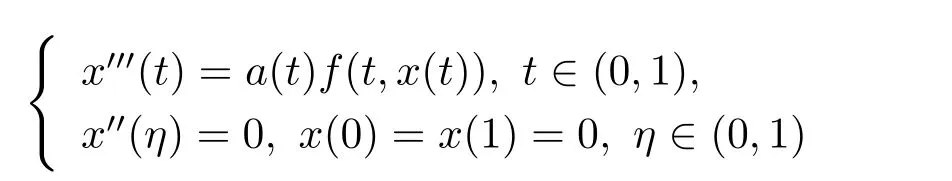
多个正解的存在性.Guo[5]利用锥上不动点定理证明了三阶三点边值问题

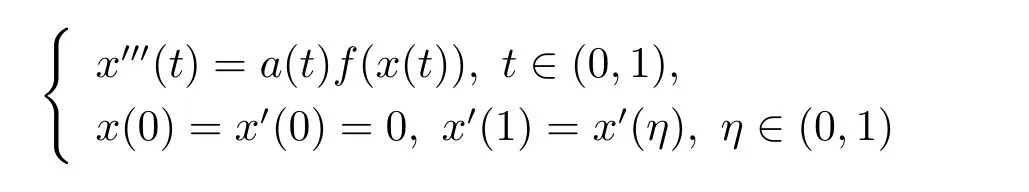
正解的存在性,其中f非负且满足超线性或次线性条件.但在这些文献中,均要求问题中非线性项非负,非线性项变号时,所得结论不再适用.目前,对具变号非线性项的三阶常微分方程多点边值问题正解的讨论比较少见.本文首先建立与问题(1.1)等价的算子方程,利用锥上不动点定理,给出了问题(1.1)正解与多个正解的存在性结论.文中允许非线性项变号,因此所得结果不同于已有文献.最后,文中给出了具体的例子解释了结论的应用性.

2　预备知识

定义2.1设E为实Banach空间.非空闭凸集P⊂E称为E上的锥,如果满足

(1)au∈P,对u∈P,a≥0;

(2)u,−u∈P,u=0.

定义2.2函数x称为[0,1]上的凸泛函,如果

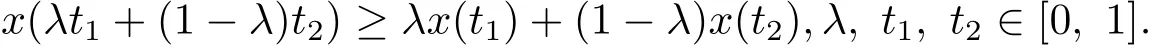
引理2.1(见文献[14])设K是Banach空间X上的锥,D为X上有界开子集,满足设全连续且x/=Ax对x∈∂DK,有如果iK(A,DK)=1,iK(A,UK)=0或iK(A,DK)=0,iK(A,UK)=1,则A在

(1) 如果‖Ax‖≤ ‖x‖,x∈ ∂DK,则iK(A,DK)=1.

(2)若存在e∈K{0}使得x/=Ax+λe,x∈∂DK,λ＞0,则iK(A,DK)=0.

(3)设U是X中有界开集中至少有一不动点.

3　主要结果与证明

首先考虑三阶微分方程边值问题

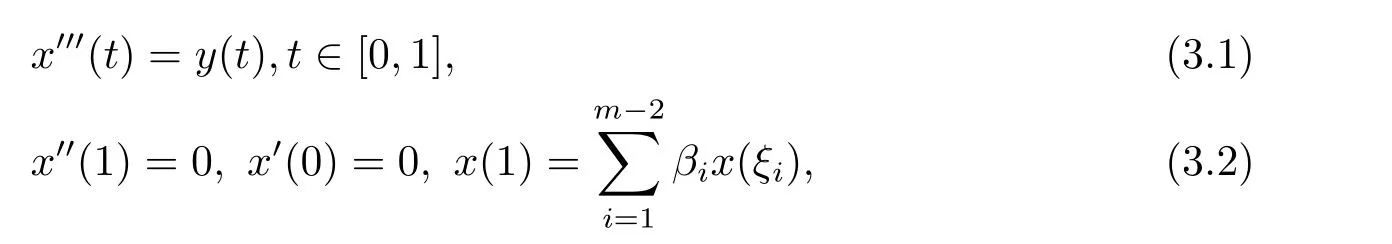
引理3.1记ξ0=0,ξm−1=1,β0= βm−1=0,y(t)∈ C[0,1],问题(3.1),(3.2)等价于

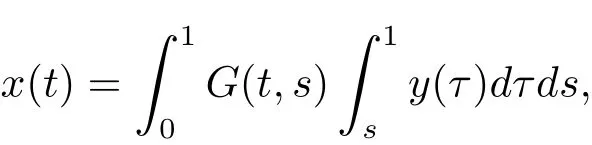
其中

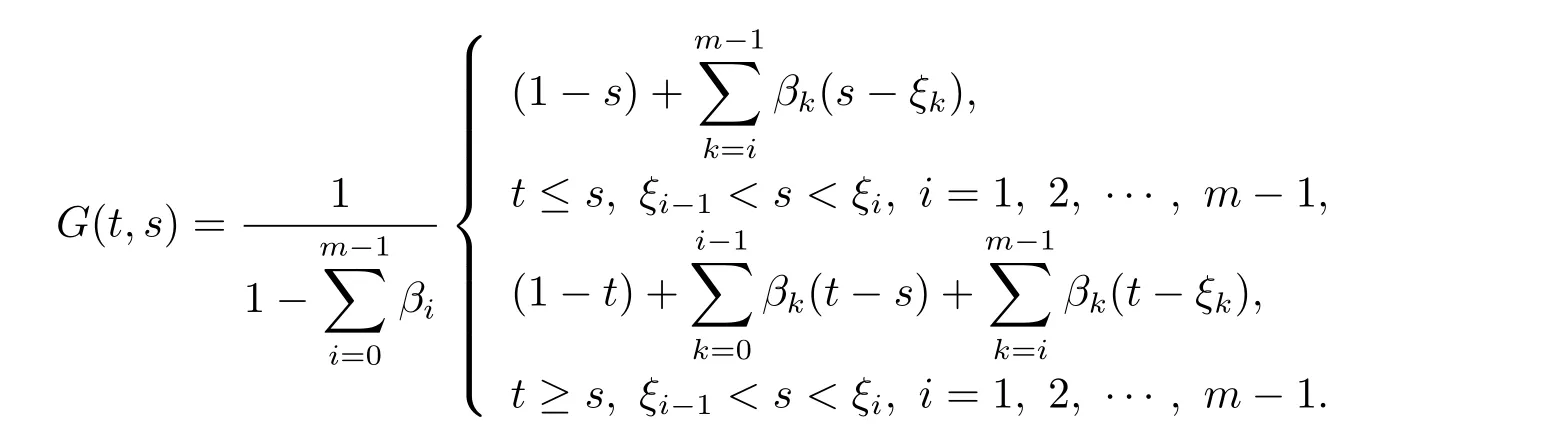
证(3.1)式两侧积分并考虑条件x′′(1)=0,有

设G(t,s)是边值问题

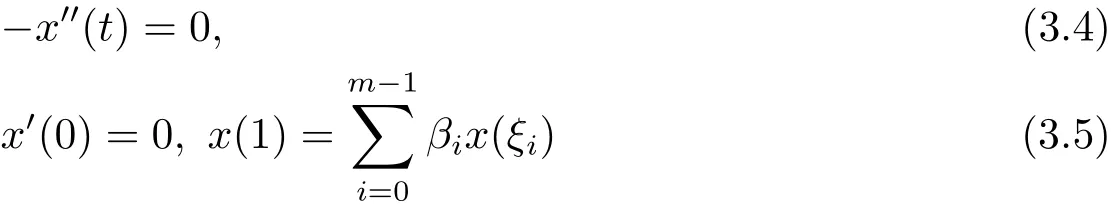
的Green函数,由(3.4)式,可设由Green函数定义及性质,结合边值条件(3.5),有

这样

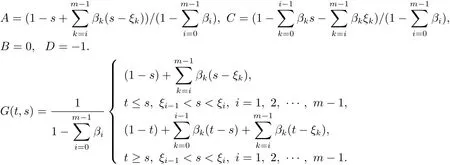
考虑(3.3)式,问题(3.1),(3.2)等价于

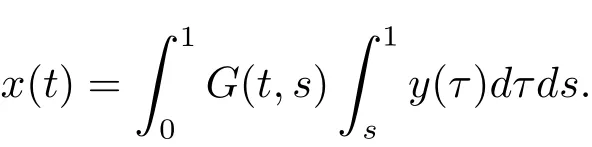
引理3.2函数G(t,s)满足G(t,s)≥0,t,s∈[0,1].

证对 ξi−1≤ s ≤ ξi,i=1,2, ···,m −1,t≤ s,

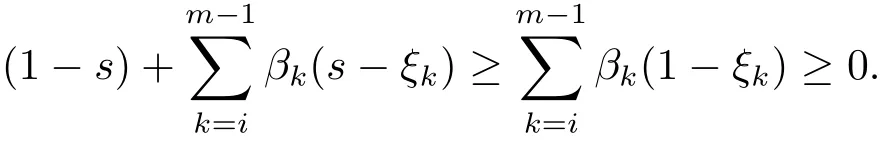
对 ξi−1≤ s ≤ ξi,i=1,2, ···,m−1,t≥ s,

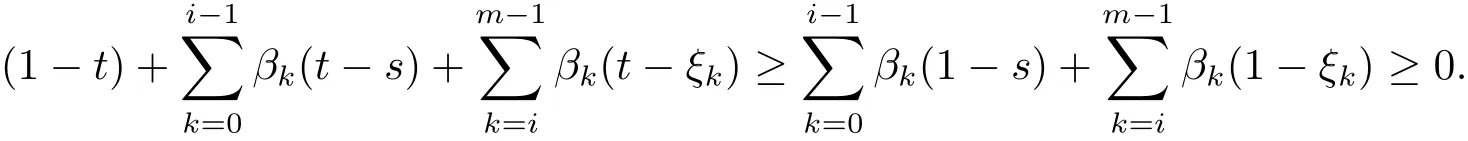
综上,G(t,s)≥0,t,s∈[0,1].

引理3.3设y(t)≥0,t∈[0,1],x(t)是边值问题(3.1),(3.2)的解,则有

其中

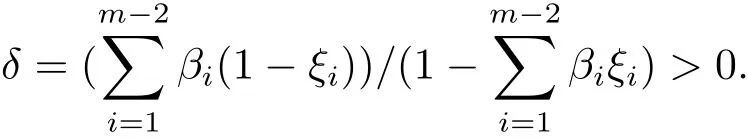
证由 x′′′(t)=y(t) ≥ 0,t ∈ [0,1]知 x′′(t) 在 [0,1]上单调递增.考虑到 x′′(1)=0,有x′′(t)≤ 0,t∈ (0,1). 结合 x′(0)=0,必有

由x(t)的凸性,

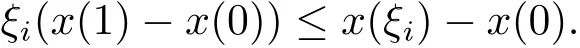
上式两端乘以βi,i=1,2,···,m−1,结合边值条件,有

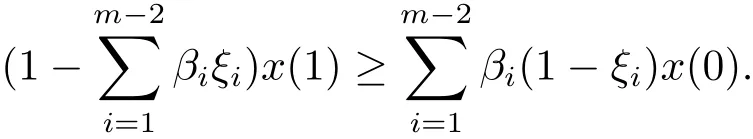
定义

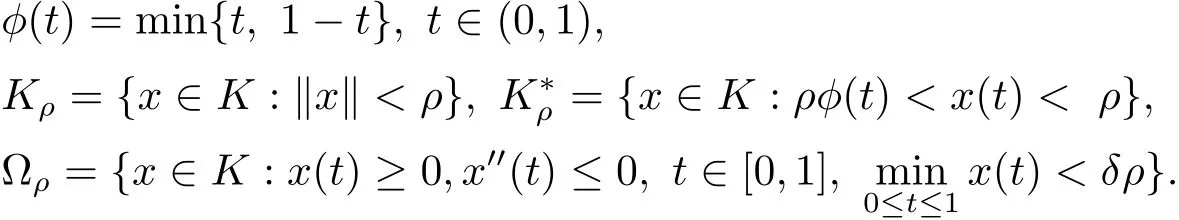
引理3.4Ωρ具有如下性质:

(1)Ωρ⊂Kρ是Kρ中开集.

(2)设x∈ ∂Ωρ,则δρ≤ x(t)≤ρ,t∈[0,1].

记

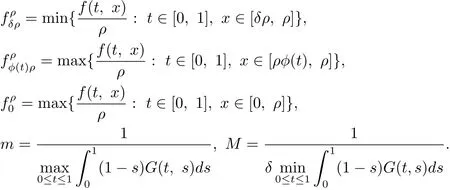
定理3.1假定条件(H)成立.此外,若条件(H1)成立:

(H1) 存在正常数ρ1,ρ2,ρ3∈ (0,∞)满足ρ1＜ δρ2＜ ρ2＜ ρ3使得

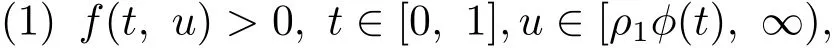
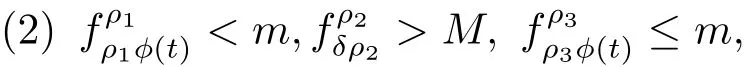
则问题(1.1)在K 中至少有三个解.假定条件(H)成立.此外,若条件(H2)成立:

(H2)存在正常数ρ1,ρ2,ρ3∈(0,∞)满足ρ1＜ρ2＜ρ3使得

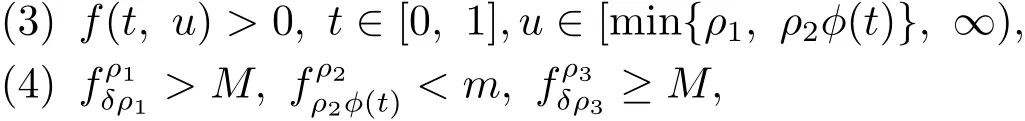
则问题(1.1)在K中至少有两个解.

证 首先设条件(H1)成立.定义辅助函数f∗(t,x)∈C([0,1]×[0,∞),[0,∞)):

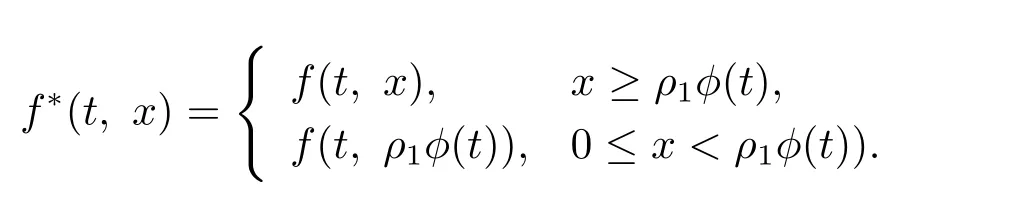
考虑如下辅助边值问题

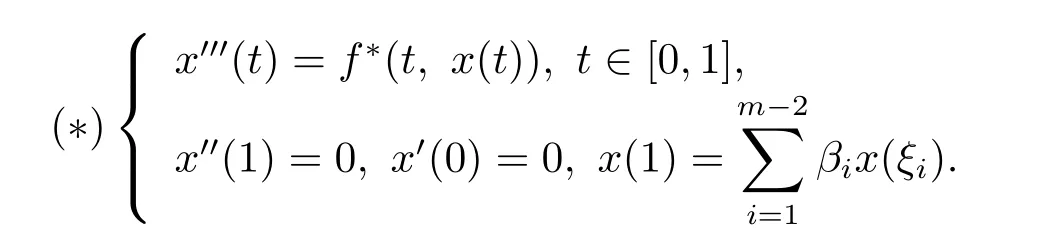
定义算子

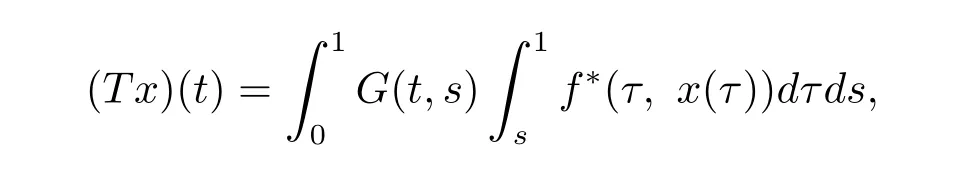
显然T:K→K是全连续的.由条件(H1),有

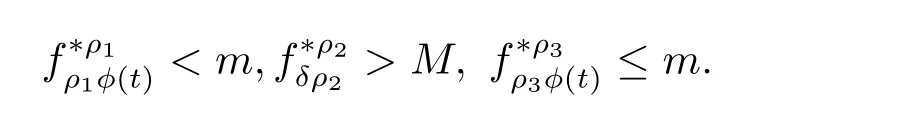
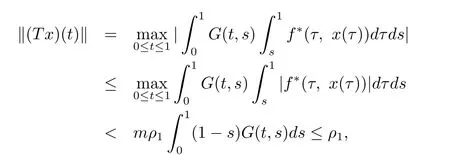
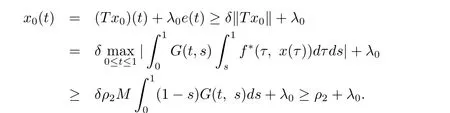
这表明ρ2≥ρ2+λ0,矛盾.由引理2.1,iK(T,Ωρ2)=0.同理可证这样,辅助边值问题存在三个正解x1,x2,x3使得

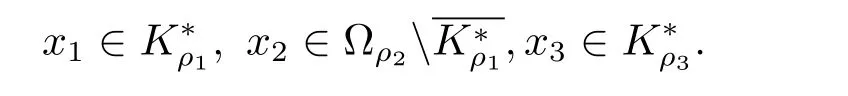
易验证辅助边值问题(∗)在[ρ1φ(t),∞)中存在三个正解x1,x2,x3,这说明边值问题(1.1)存在至少三个正解.条件(H2)成立时,正解的存在性同理可证.完全类似定理3.1,可证得如下结论.

定理3.2设条件(H)成立.此外,下列条件之一成立:

(H3)存在正常数ρ1,ρ2∈(0,∞)满足ρ1＜δρ2使得

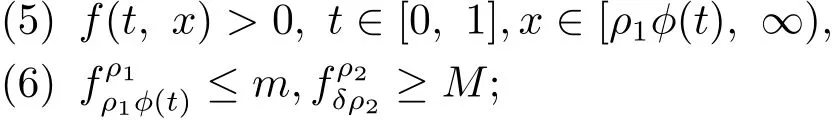
(H4)存在正常数ρ1,ρ2∈(0,∞)满足ρ1＜ρ2使得

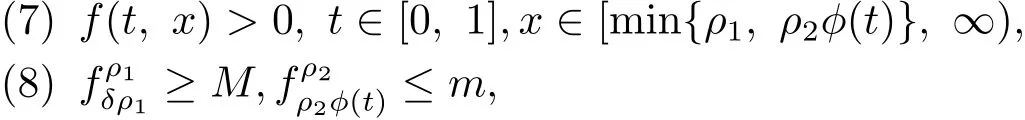
则边值问题(1.1)在K中至少有一正解.

4　例子

考虑如下三阶四点边值问题

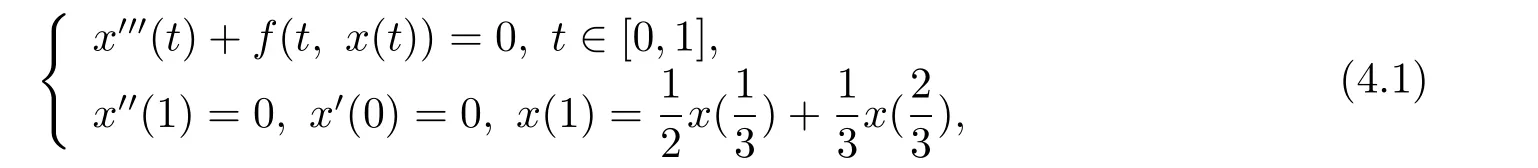
其中

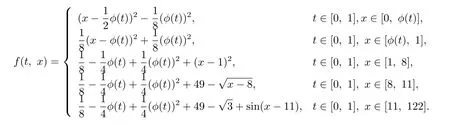
计算可得函数G(t,s)由下式给出

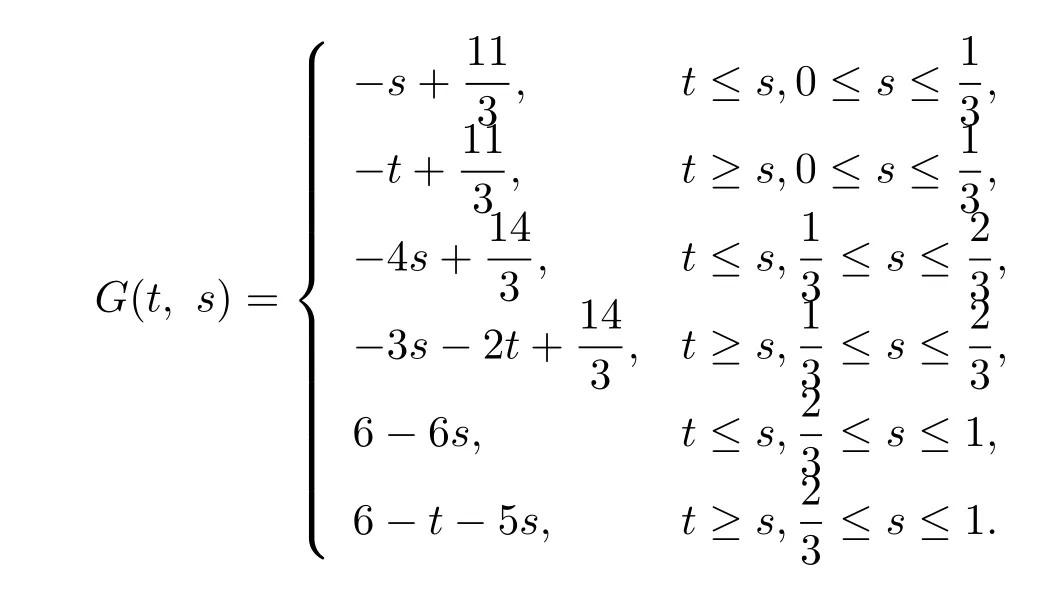
取 ρ1=1,ρ2=11, ρ3=122,有易验证f(t,x)满足条件(H)和

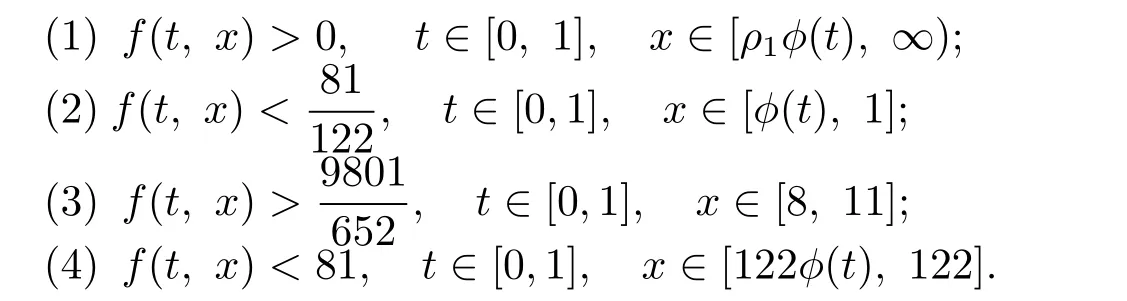
这样定理3.1的所有条件均满足,因此,问题(4.1)至少存在三个单调递增的凸正解.

注 问题(4.1)中非线性项是变号的,已有文献中对三阶边值问题正解存在性的讨论,就作者所知,均无法适用此问题.

[1]Gregus M.Third order linear differential equations[J].Math.Appl.,Reidel,Dordrecht,1987,11(3):919–944.

[2]Anderson D R.Multiple positive solutions for a three-point boundary value problem[J].Math.Comput.Model.,1998,27(6):49–57.

[3]Palamides P,George Smyrlis.Positive solutions to a singular third-order three-point boundary value problem with an indefinitely signed Green’s function[J].Nonl.Anal.,2008,68:2104–2118.

[4]Guo D,Lakshmikantham V.Nonlinear problems in abstract cones[M].New York:Academic Press,1988.

[5]Guo L,Sun J,Zhao Y.Existence of positive solutions for nonlinear third-order three-point boundary value problems[J].Nonl.Anal.,2008,68:3151–3158.

[6]Hopkins B,Kosmatov N.Third-order boundary value problems with sign-changing solutions[J].Nonl.Ana.,2007,67:126–137.

[7]Chu J,Zhou Z.Positive solutions for singular non-linear third-order periodic boundary value problems[J].Nonl.Ana.,2006,64:1528–1542.

[8]Graef J,Kong L.Positive solutions for third order semipositone boundary value problems[J].Appl.Math.Lett.,2009:22:1154–1160.

[9]Lin X,Du Z,Liu W.Uniqueness and existence results for a third-order nonlinear multi-point boundary value problem[J].Appl.Math.Comput.,2008,205:187–196.

[10]Minghe P,Chang S.Existence and uniqueness of solutions for third-order nonlinear boundary value problems[J].J.Math.Anal.Appl.,2007,327:23–35.

[11]Li S.Positive solutions of nonlinear singular third-order two-point boundary value problem[J].J.Math.Anal.Appl.,2006,323:413–425.

[12]Yao Q.Positive solution for a semi-linear third-order two-point boundary value problem[J].Appl.Math.Lett.,2004,17:1171–1175.

[13]Ji D,Feng M,Ge W.Multiple positive solutions for multipoint boundary value problems with sign changing nonlinearity[J].Appl.Math.Comput.,2008,196:511–520.

[14]Lan K Q.Multiple positive solutions of semi-linear differential equations with singularities[J].J.London Math.Soc.,2001,63:690–704.