零级Dirichet级数的增长性及其Dirichlet-Hadamard乘积

崔永琴,周凤麟,徐洪焱

(景德镇陶瓷大学信息工程学院,江西景德镇 333403)

1　引言及相关结果

考虑Dirichlet级数

其中{an}是复数列,0＜λn↑∞,s=σ+it(σ,t是实变量).当级数(1.1)满足

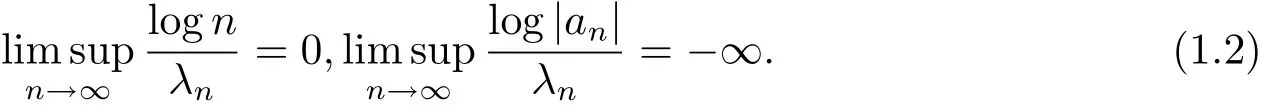
这时,根据文[1–2]的Valiron公式可得级数(1.1)的收敛横坐标及绝对收敛横坐标都是+∞,那么其和函数f(s)在全平面内解析,即为整函数.

记f(s)的最大模,最大项为

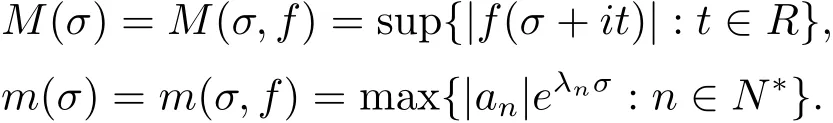
定义1.1[3]若f(s)是满足(1.2)式的整函数,那么f(s)的级ρ定义为

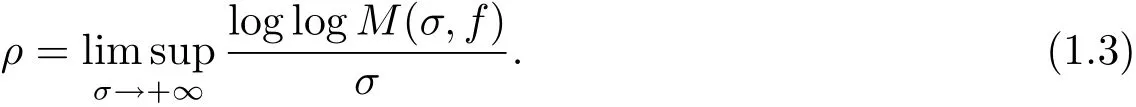
若ρ=0,级数(1.1)是全平面上的零级Dirichlet级数.此时定义该级数(1.1)的对数级ρ∗为

当ρ∗∈(1,+∞)时,Dirichlet级数的对数型T∗如下

关于整函数的增长性的问题,Hardy、余家荣、孙道椿、高宗升等已经得到了许多经典的结论[1−2,4−6].Sayyed,Metwally[7]讨论了泰勒级数的对数级,而对复平面上的零级Dirichlet级数增长性的研究较少.2006年,田宏根、孙道椿、郑承民在相对较宽的条件下,对该问题进行深入的研究并得到了由系数表示的零级Dirichlet级数的对数级的结果.

定理A[3]若f(s)是满足(1.2)式的整函数,则

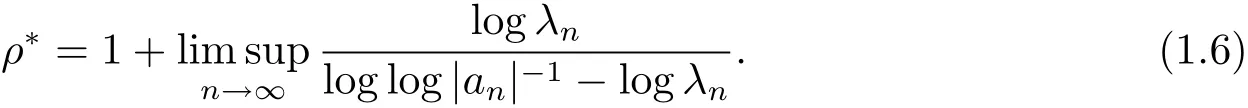
本文将继续研究了零级Dirichlet级数的对数型,得到如下结果.

定理1.1若f(s)是满足(1.2)式的整函数,则

这里

2009年,孔荫莹在文[9–10]构造了Dirichlet-Hadamard乘积并得到了有限级及无穷级Dirichlet级数在该乘积下的增长性的相关结果.2015年,崔永琴等在文[11]构造了新型的Dirichlet-Hadamard乘积进一步推广了文[9,10]的结果.

然而,对于零级Dirichlet级数的Hadamard乘积的增长性并未有人涉及.本文将主要考察零级Dirichlet级数的Dirichlet-Hadamard乘积的对数级与对数型,在介绍主要结果前,我们先给出如下Dirichlet-Hadamard乘积定义.

定义1.2[11]若且f1(s),f2(s)是满足(1.2)式的整函数.若α,β为两个实常数满足0＜α,β＜∞,构造它们的Dirichlet-Hadamard乘积如下

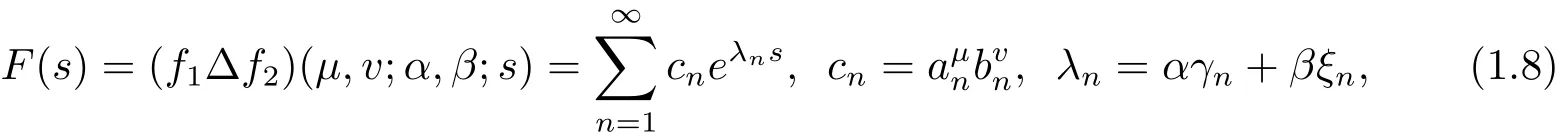
其中µ和v是正实数;{an},{bn}⊂C,0＜γn,ξn↑∞.

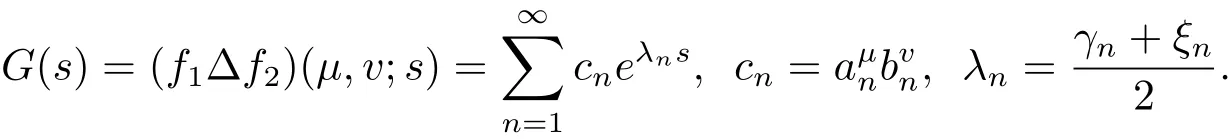
定理1.2若f1(s),f2(s)是满足(1.2)式的整函数,它们的对数级分别为,且

则 Dirichlet-Hadamard 乘积 F(s) 的对数级 ρ∗满足特别地,当时,F(s)的对数型T∗满足

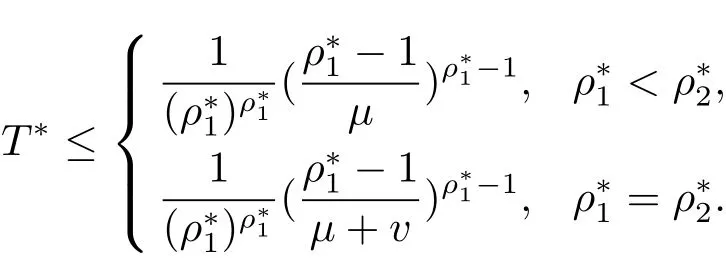
推论1.1若f1(s),f2(s)是满足(1.2)式的整函数,它们的对数级分别为和且满足 (1.9)式,则其 Dirichlet-Hadamard 乘积 G(s)的对数级 ρ∗满足特别地,当对数型 T∗满足

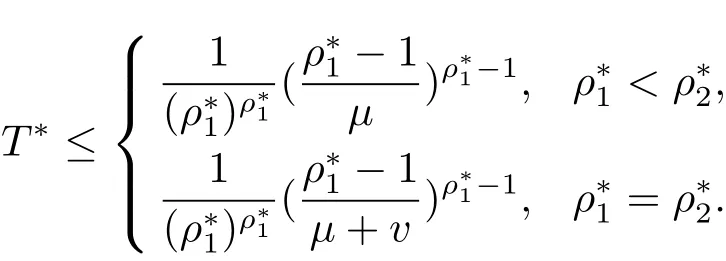
接下来,在放宽条件的前提下进一步讨论Dirichlet-Hadamard乘积形式的增长性,得到如下结果.

定理1.3若f1(s),f2(s)是满足(1.2)式的整函数,它们的对数级分别为和,且

则其 Dirichlet-Hadamard 乘积 F(s) 的对数级 ρ∗满足特别地,当F(s)对数型T∗满足

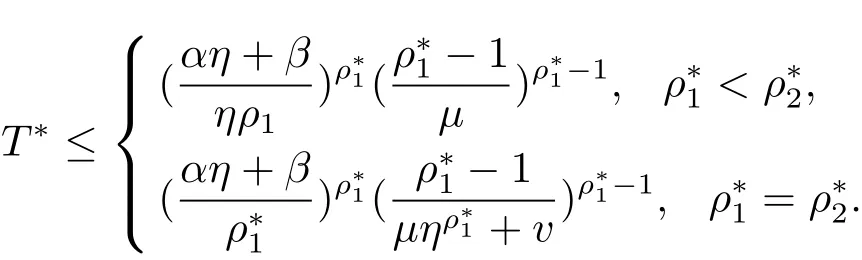
推论1.2若f1(s),f2(s)是满足(1.2)式的整函数,它们的对数级分别为和且满足 (1.10) 式,则其 Dirichlet-Hadamard 乘积 G(s) 的对数级 ρ∗满足当对数型 T∗满足

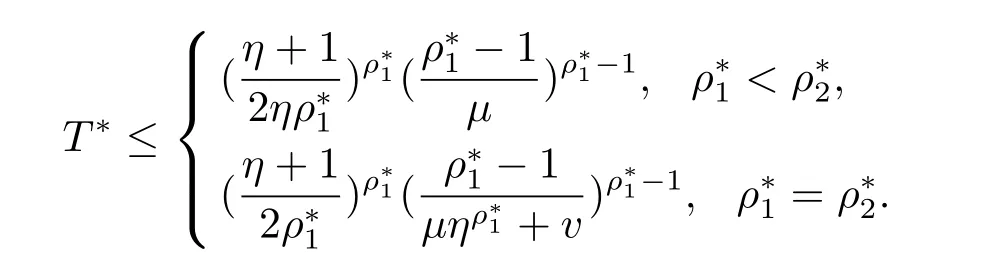
2　若干引理

引理2.1[11]若f1(s),f2(s)是满足(1.2)式的整函数,且满足(1.9)式,那么其Dirichlet-Hadamard乘积F(s)是整函数.

引理2.2若f1(s),f2(s)是满足(1.2)式的整函数,且满足(1.10)式,那么其Dirichlet-Hadamard乘积F(s)是整函数.

证

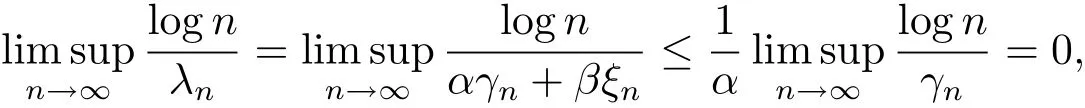
又

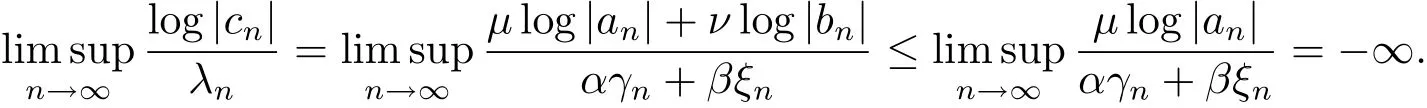
所以其Dirichlet-Hadamard乘积F(s)是整函数.

引理2.3若a,b(b＞ 1)是一正的常数,x是任一正实数,那么函数ψ(σ)=aσb−时达到最小值

证由令 ψ′(σ)=0 解得

引理2.4若a,b(b＞1)是一正的常数,σ是任一实数,那么函数在时达到最大值

3　定理的证明

定理1.1的证明 先证

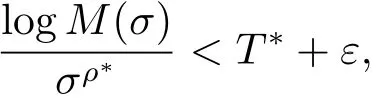
从而

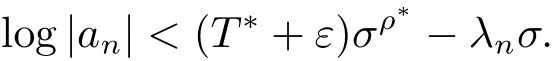
由T∗的定义知,∀ε＞0,有充分大的σ使则

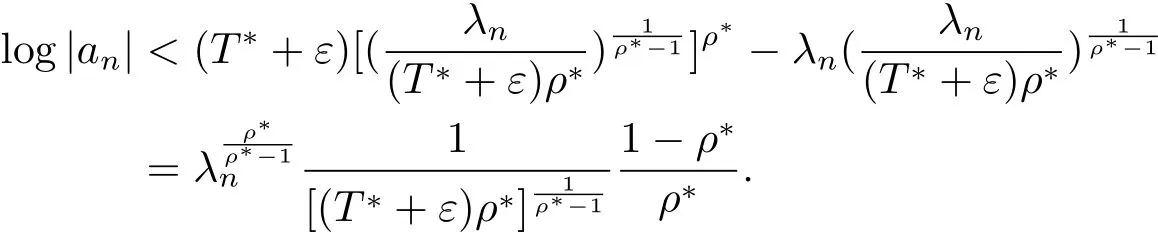
所以

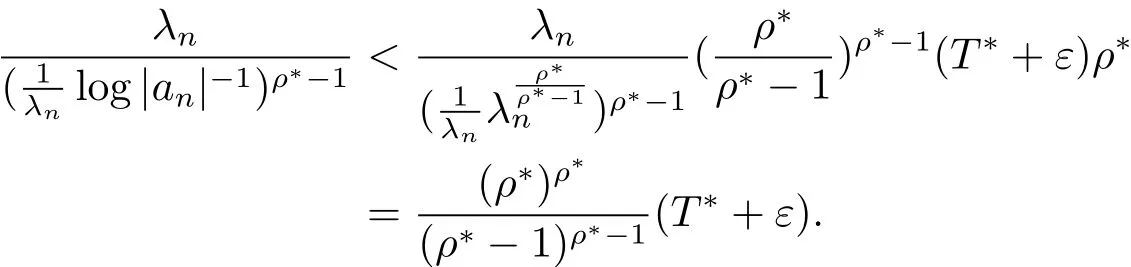
由ε的任意性知

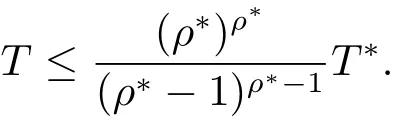
假设等号不成立,即存在T1使得于是存在 N1＞ 0,当 n ＞ N1时,

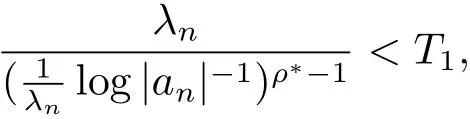
即

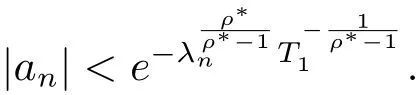
由(1.2)式知存在一常数M,N2＞N1,使得n＞N2时有λn＞M logn,于是

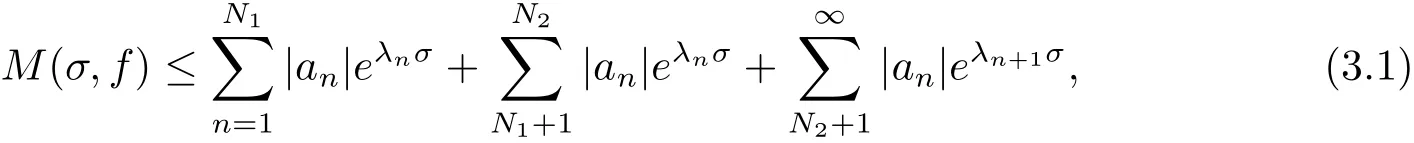
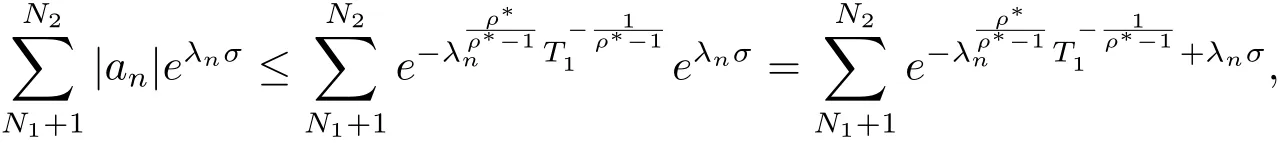
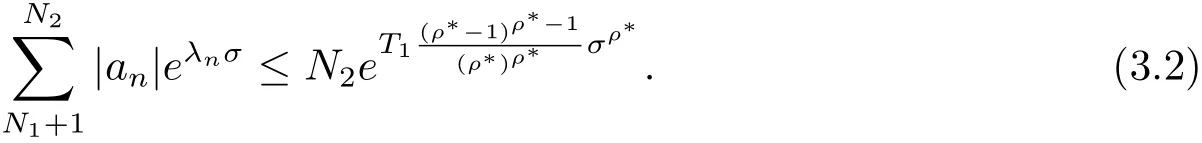
再由(1.2)式知λn+1≤(1+ε)λn,对所有的n∈N+成立,记所以

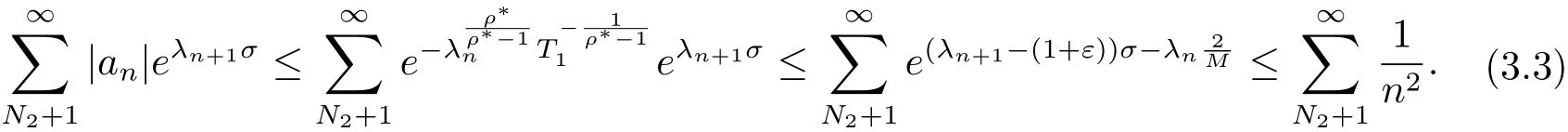
由(3.1)–(3.3)式知,对充分大的σ有

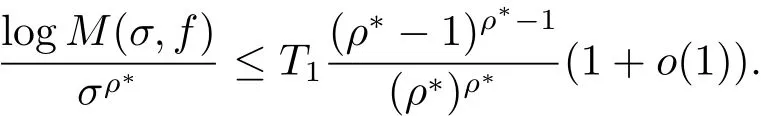
定理1.2的证明由定理A可知∀ε＞0,存在两个正整数N1,N2,当n＞N=max{N1,N2}时,有

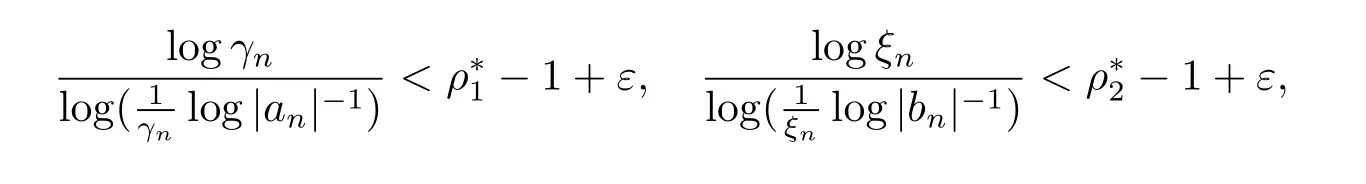
即

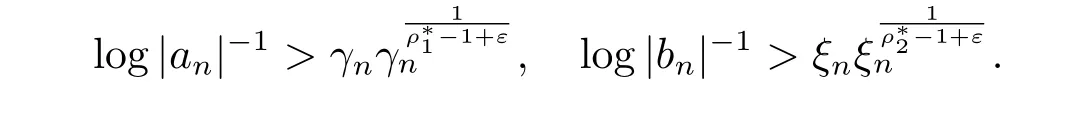
由cn的定义有

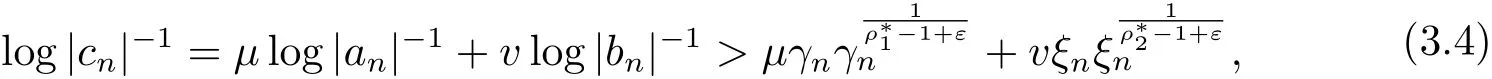
则

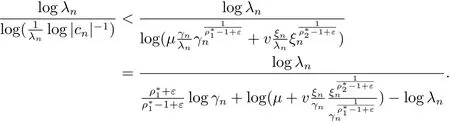
由于 λn= αγn+βξn,γn～ ξn(n → ∞),可得

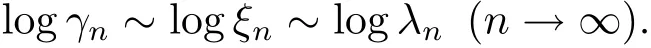
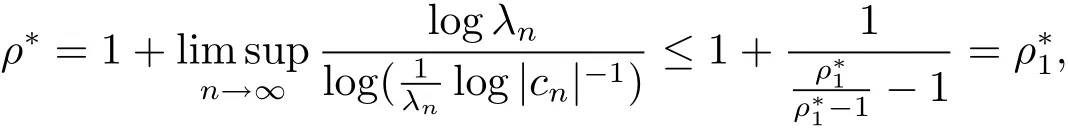
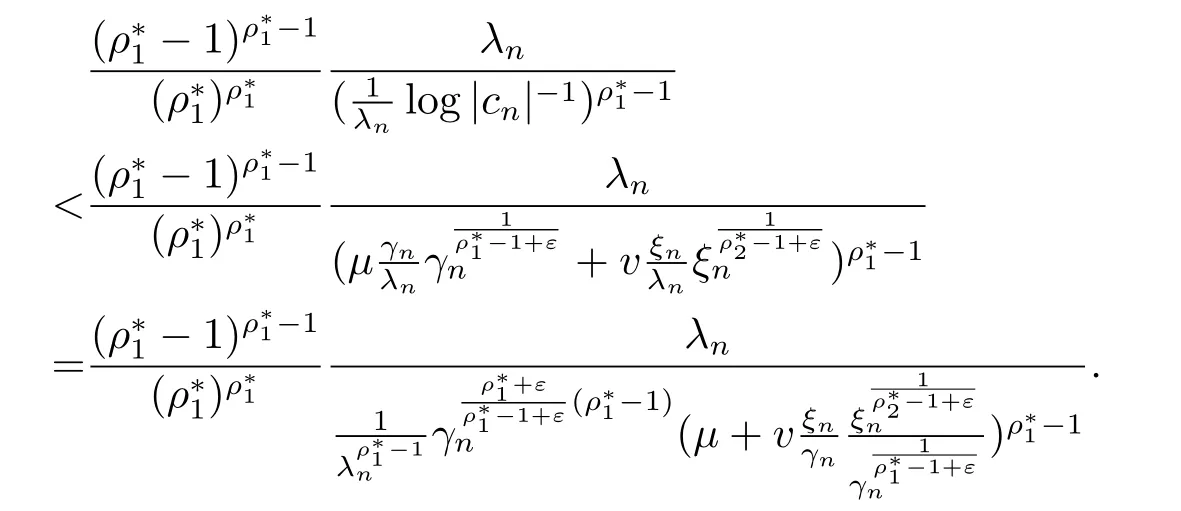
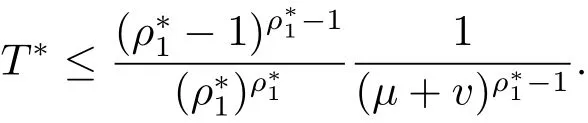
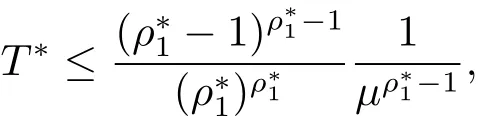
故定理1.2得证.

定理1.3的证明类似于定理1.2的证明:∀ε＞0,存在两个正整数N1,N2,当n＞N=max{N1,N2}时有

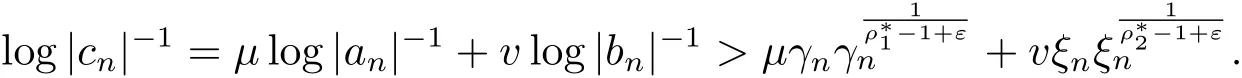
由 γn= ηξn,有于是

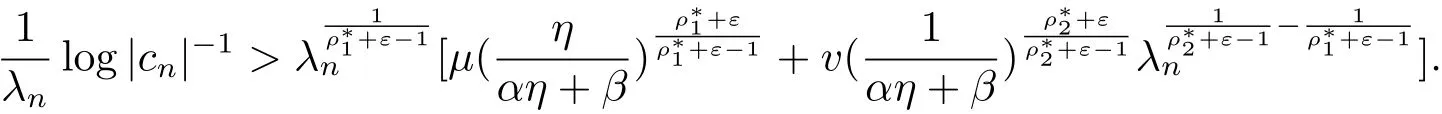
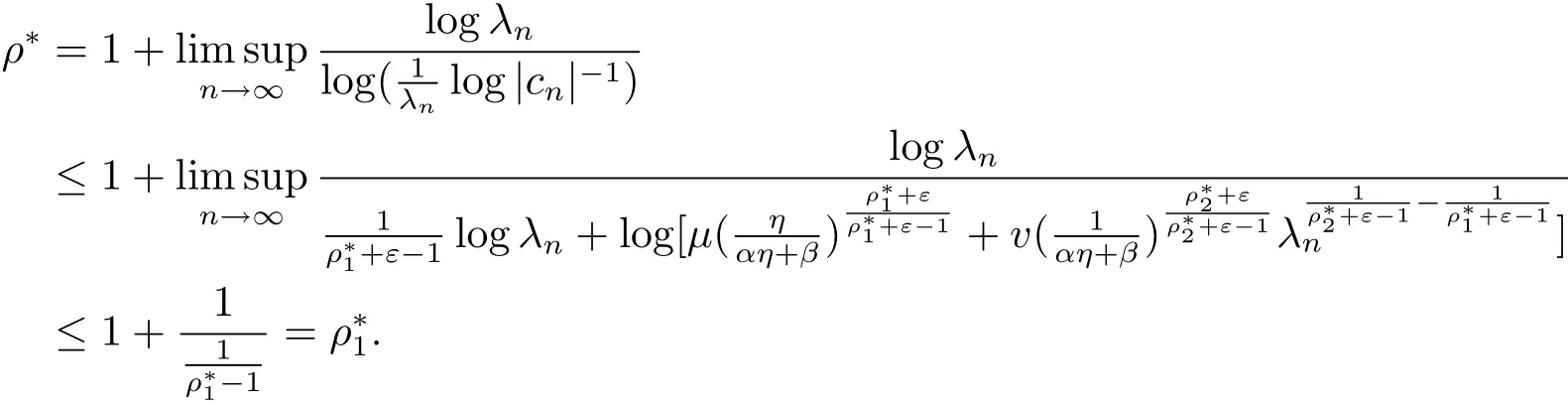
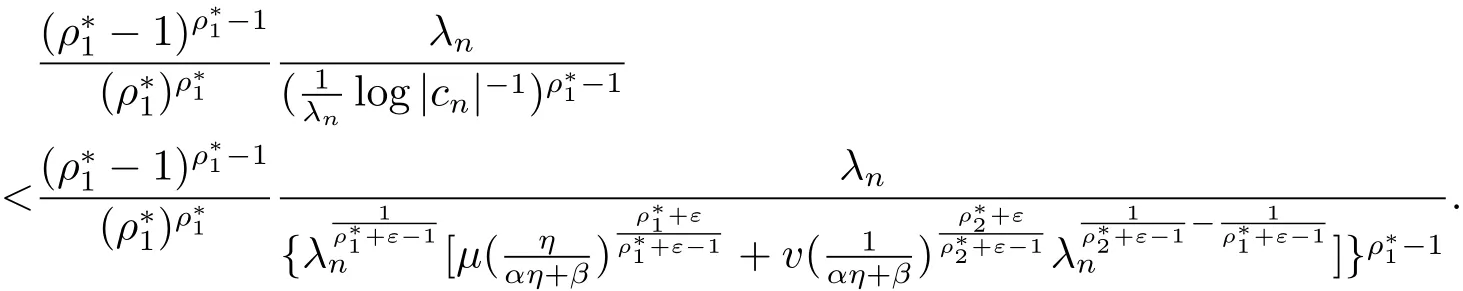
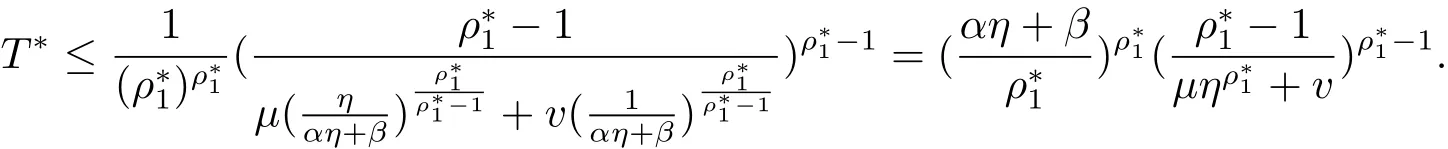
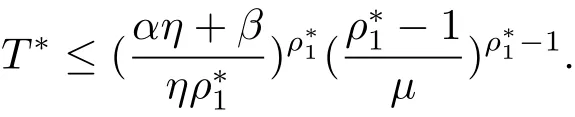
故定理1.3得证.

[1]Hardy G H,Riesz M.The general theory of Dirichlet series[M].New York:Stechert-Hafner,Inc,1964.

[2]余家荣,丁晓庆,田范基.Dirichlet级数与随机Dirichlet级数的值分布[M].武汉:武汉大学出版社,2004.

[3]田宏根,孙道椿,郑承民.平面上的零级Dirichlet级数[J].系统科学与数学,2006,26(3):270–276.

[4]高宗升.Dirichlet级数表示的整函数的增长性[J].数学学报,1999,42(4):741–748.

[5]高宗升,孙道椿.无限级随机Dirichlet级数的值分布[J].数学年刊,1993,14(6):677–685.

[6]贺隆贞.关于狄里克莱级数确定的整函数的(p,q)(R)型和下(p,q)(R)型[J].武汉大学学报(自然科学版),1985,4:17–26.

[7]贺隆贞.关于狄里克莱级数确定的整函数的(p,q)(R)级和下(p,q)(R)型[J].武汉大学学报(自然科学版),1983,3:73–89.

[8]Sayyed K A M,Metwally M S.Logarithmic order and logarithmic type of functions and sets of polynomials of two complex variables[J].Bull.Fac.Fac.Sci.Qena(Egypt),1994,2(2):127–140.

[9]孔荫莹.Dirichlet-Hadamard乘积的q-级与q-型[J].数学学报,2009,52(6):1165–1172.

[10]孔荫莹,邓冠铁.Dirichlet级数的Dirichlet-Hadamard乘积[J].数学年刊,2014,35(2):145–152.

[11]崔永琴,汤文菊,徐洪焱.Dirichlet级数及其新型Dirichlet-Hadamard乘积的增长性[J].数学的实践与认识,2015,45(22):267–273.