地层塌陷作用下埋地管道应变响应分析

张　杰，梁　政，韩传军，张　瀚

(西南石油大学 机电工程学院，成都 610500)

0　引言

油气管道担负着石油、天然气输送任务，是国民经济的重要大动脉之一。目前我国油气管道主要采用埋地敷设，如西气东输、川气东送、兰成渝等大口径长输油气管道的主要输送段均采用埋地敷设。由于管道埋在地下，受地层影响较大，特别是管道穿越黄土、丘陵、煤矿采空区等易塌陷地层时，易发生弯曲变形、裸露、悬空，甚至断裂[1]。欧洲石油行业协会(CONCAWE)对1971～2000年运行的欧洲管道进行了事故统计，由自然灾害导致的事故14起，其中10起是由山体滑坡或地基塌陷引起的[2]。2014年我国西南某气矿统计了影响所属管段的地质灾害敏感点180处，其中地面塌陷占5%。因而，对塌陷地段的管道力学行为研究具有重要的工程应用价值。

关于地层塌陷对埋地管道影响问题，一种是考虑围土完全塌陷形成管道悬空，另一种是仅有下部地层塌陷，上部地层发生大变形，管道未形成悬空。关于未形成悬空管道，文献[3]中提及某日本学者基于弹性地基和连续梁模型建立了受沉降作用的埋地管道简化分析公式；高惠瑛等[3]提出了不均匀沉降下埋地管道的几何大变形方程；Ariman等[4]基于管道为弹性各向同性的薄圆柱壳假设提出了圆柱壳理论；梁政[5]基于弹性地基梁模型分析了埋地管道的变形与受力；尚尔京等[6]利用Winkler地基梁模型与理想弹塑性地基梁模型对塌陷区段的埋地管道进行了分析；王晓霖等[7]提出了开采塌陷区埋地管道的最大应力与应变简化评定公式；Yuan等[8]建立了海底滑坡作用下的管道变形解析模型。目前，关于地层塌陷对埋地管道影响的理论研究主要是基于弹性理论和梁单元模型，研究管道在沉陷作用下的弯曲变形，得到管道应变、应力分布，但未考虑管土相互作用，且在围土变形作用下整个管道的轴向摩擦力并非均匀分布。同时，由于管道为薄壳结构，采用梁模型分析管道屈曲行为较为困难；因此，本研究以黄土地层埋地管道未形成悬空为例，基于有限元原理和弹塑性理论，建立下部地层塌陷作用下埋地管道挠曲变形的数值计算模型，研究沉降量、壁厚、埋深及土体参数对管道应变响应的影响规律。

1　塌陷区埋地管道基本特征

地下矿场采空区、硐室等发生垮塌，或下部地层在渗流作用下发生沉降等造成上部岩土发生下沉，并会在地表形成周围高、中央低的盆地结构(图1)。根据塌陷区的特点，可将埋地管道分为4个区域：BC管段对应中间塌陷区，AB管段对应内过渡塌陷区，OA管段对应外过渡塌陷区，DO管段对应非塌陷区。

图1　地层塌陷及管道挠曲变形示意图Fig.1　　　　Schematic diagram of strata subsidence and pipeline bending deformation

位于塌陷地层正上方的为中间塌陷区，该段地表下沉相对较为均匀，地面形貌与塌陷之前变化较小，地表下沉量最大[9]；内过渡区为中间塌陷区和外过渡区的过渡地带，该段地表塌陷不均匀，靠近中间区的下沉量大于靠近外过渡区一侧，呈现出凹形，并产生压缩变形；外过渡区的变形主要是由于岩土内部的粘聚力及管道压缩下层岩土变形而引起的，其下沉量分布不均匀，地面向盆地中心倾斜，呈现为凸形；非塌陷区离塌陷盆地较远，地表几乎不发生沉降。

2　数值计算模型

一般应用索模型和梁模型分析管道的屈曲破坏较为困难[10]。管道为薄壁壳结构，当其截面存在大变形时，管道的轴向应变与弯曲应变相互影响，不能简单叠加[10]。在地层塌陷过程中，管道还会出现残余应力和应力集中，因而采用有限元方法进行分析更为适宜。

在建模过程中需要考虑管材与土体的非线性特性、管土耦合、管道屈曲及土体大变形等因素。建立常用油气输送管道的管土耦合模型如图2所示。管径为914.4 mm、壁厚为8 mm；按照工程实际，选取管道埋深约为2倍管径；整个模型轴向方向长度约为60倍管径，横向和纵向方向约为10倍管径。则整个模型在x、y、z方向尺寸为60 m×10 m×10 m，管道中心距离地表2.5 m。采用0.1 m的四节点壳单元对管道进行网格划分[11]，采用六面体单元对土体进行网格划分，对管道周围土体进行网格细化。

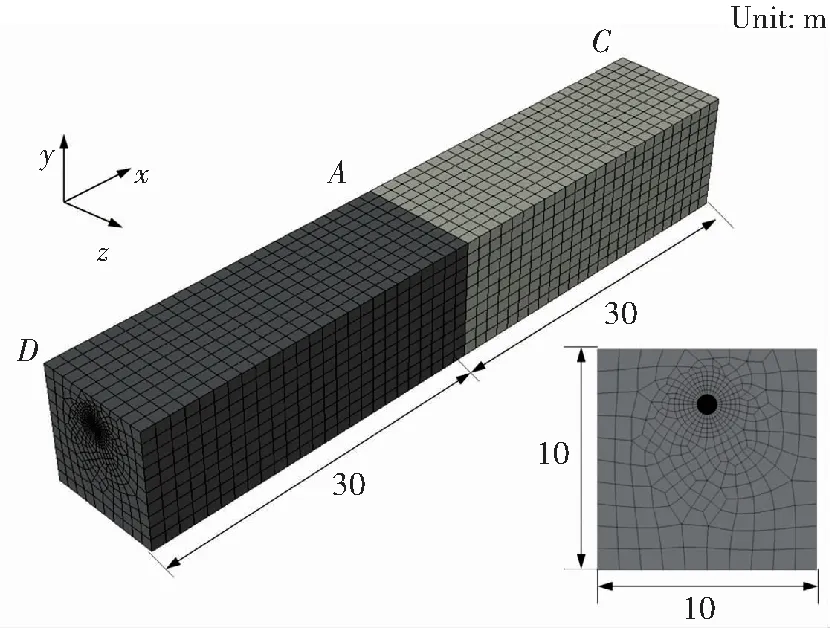
图2　有限元计算模型Fig.2　Finite element model of the soil and pipeline

根据前文，将围土模型沿x方向分为塌陷区和非塌陷区2个部分。整个分析过程分为两步，对整个模型施加重力载荷及对塌陷区土体施加位移载荷。模型上表面为自由面以模拟地表，对非塌陷区土体下表面的y方向约束，对塌陷区土体下表面施加位移载荷，以模拟下部地层塌陷，对非塌陷区块的端面及管道端面施加x向约束。由于建立了1/2对称模型，因而对塌陷区块的端面及管道端面施加x向对称约束。埋地管道与围土之间的相互作用既属于耦合作用问题也属于接触问题。有限元软件中大型的单元库和广泛的求解非线性问题的能力及高效率辅助系统，可以较好地模拟管土之间的非线性耦合和接触问题。本文采用罚函数摩擦模型(其基本原理是在每一个时间步首先检查各从节点是否穿透主面，若没有穿透则不做处理，若穿透则在该从节点与被穿透主面间引入一个较大的界面接触力，其大小与穿透深度、主面的刚度成正比。允许接触面有“弹性滑移”，适用于大多数的接触问题)定义管土表面接触，定义接触面之间摩擦系数为0.3。

管材钢为弹塑性材料，以X65钢管为例分析，管材屈服强度为448.5 MPa，弹性模量为210 GPa，泊松比为0.3，密度为7.8×103kg/m3[12]。地层土体为黄土，材料选用理想弹塑性Mohr-Coulomb模型，粘聚力c=24.6 kPa，内摩擦角φ=11.7°，弹性模量E=33 MPa，密度ρ=1.4×103kg/m3，泊松比υ=0.45[13]。

3　计算结果分析

3.1　地层塌陷量

当地层塌陷量较小时，塌陷区管道随地层同时下沉，并发生弯曲变形；当地层塌陷量较大时，埋地管道会被拉断或形成悬空。图3为塌陷量取不同值时X65管道变形曲线，可见管道变形随着塌陷量增大而增大，且呈非线性规律。管道挠曲变形主要发生在OB段，而非塌陷区DO段管道变形较小。

图4为管道最大轴向应变随沉降量变化曲线，随着地层沉降量增大，管道最大轴向应变呈非线性规律增大。管道的轴向应变主要出现在OA段，而非沉陷区DO段的轴向应变较小。且不同地层沉降作用下的管道轴向应变分布不同。当沉降量为2 m时，管道M、N点处(M为管道顶部，N为管道底部)的最大轴向拉、压应变绝对值较为接近，且沿轴向方向的出现了波动(即管道顶部和底部沿轴向均有拉、压应变)。当地层沉降量为6m时，上部M点的最大轴向应变逐渐增大，且范围逐渐减小；而N点的拉应变范围逐渐减小，OA段顶部的压应变逐渐向中间沉陷区靠近。从整个数值模拟过程来看，M点处的拉应变最大，且该值随着地层沉降量的增大而呈非线性规律逐渐增大。因而，沉陷区管道最容易在OA段出现拉断，这也与现场管道失效调查结果相同。

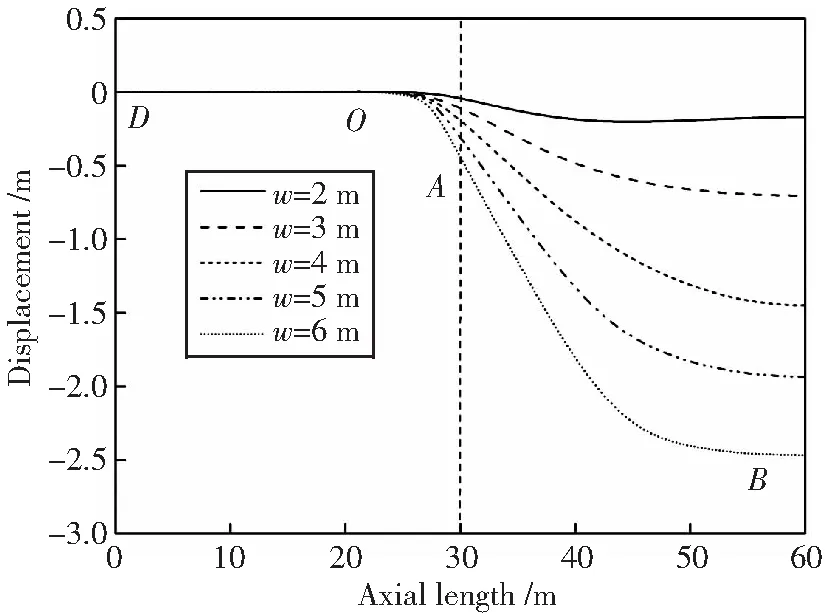
图3　不同塌陷量下管道挠曲线Fig.3　Deflection curves under different subsidence quantity

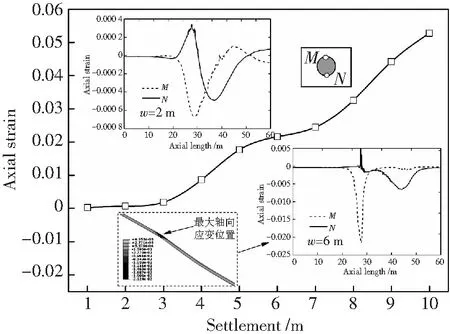
图4　不同塌陷量下管道轴向应变Fig.4　Axial strain curve under different subsidence quantity

3.2　管道壁厚

当沉降量为6 m时，不同壁厚管道挠曲线如图5所示。无论壁厚取何值，管道A点(对应于30 m处)的下沉量基本保持不变，说明两个区块错位点处的管道下沉量与管道径厚比无关；壁厚越小，管道AB段的下沉量越大，即整个管道最大下沉量越大；而OA段管道曲率半径越小，即管道弯曲变形越大，更易发生失效。说明随着壁厚减小，管道抗变形能力逐渐减弱。

由图4可知，管道OA段顶部的拉应变大于其他部位，是导致其失效的主要原因，因而后续均是对该部位管段的最大轴向应变进行讨论。图6为不同壁厚管道顶部最大轴向应变曲线。随着壁厚增大，管道轴向应变逐渐减小。且沉降量越大，管道轴向应变随壁厚的变化趋势越明显；这表明增加管道壁厚可以增强其抗变形能力，降低其失效概率；但当地层沉降量较小时，增加壁厚对管道轴向应变影响较小。

图5　不同径厚比管道的挠曲线Fig.5　Deflection curves under different wall thicknesses

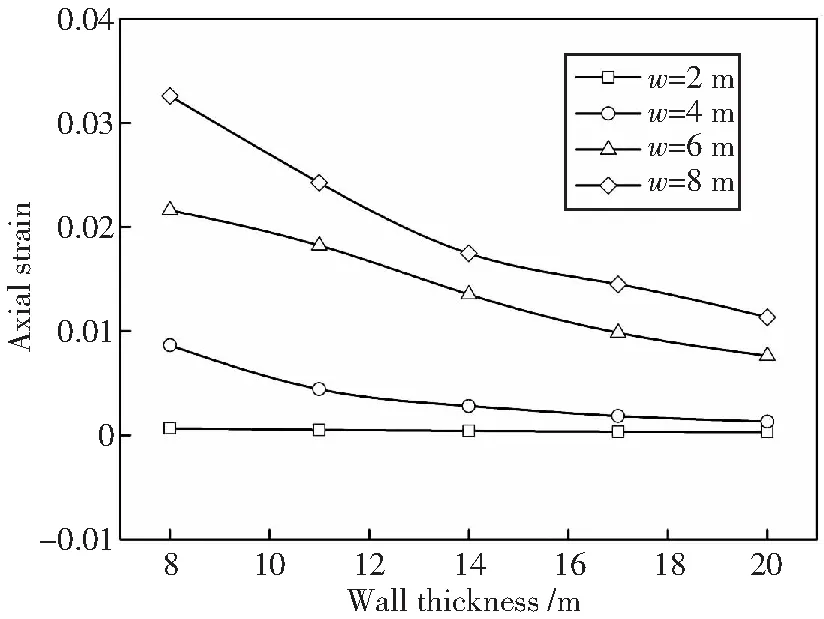
图6　不同壁厚下管道最大轴向应变Fig.6　Axial strain curve under different wall thicknesses

3.3　管道埋深

管道埋深不同，则其承受的地应力不同，埋深越深，围土对其产生载荷越大。由于管土耦合作用，围土的粘聚力对管道变形影响较大。当地层沉降量为5 m，围土粘聚力为24.6 kPa时，不同埋深的管道挠曲线如图7所示。DO管段基本保持不变，但随着埋深增大，管道挠曲变形逐渐减小。当地层发生塌陷时，管道各部分除了需要克服相邻部分的拉压应力、围土摩擦力外，还需要对上覆土下沉产生阻抗力。由于上覆土粘聚力较大，在管道作用下形成的土拱效应较强，特别是随着埋深的加深，土拱效应越强，上覆土的变形越大，则埋地管道相对下沉量就越小，因而管道的挠曲变形就越小。

当地层沉降量为5 m，围土粘聚力为24.6 kPa时，不同埋深下管道顶部最大轴向应变如图8所示。随着埋深增大，管道轴向应变逐渐减小。当埋深小于3 m时，轴向应变变化率较大；而当埋深大于3 m时，管道轴向应变变化较小；当沉降量较小时，埋深对管道应变影响较小。

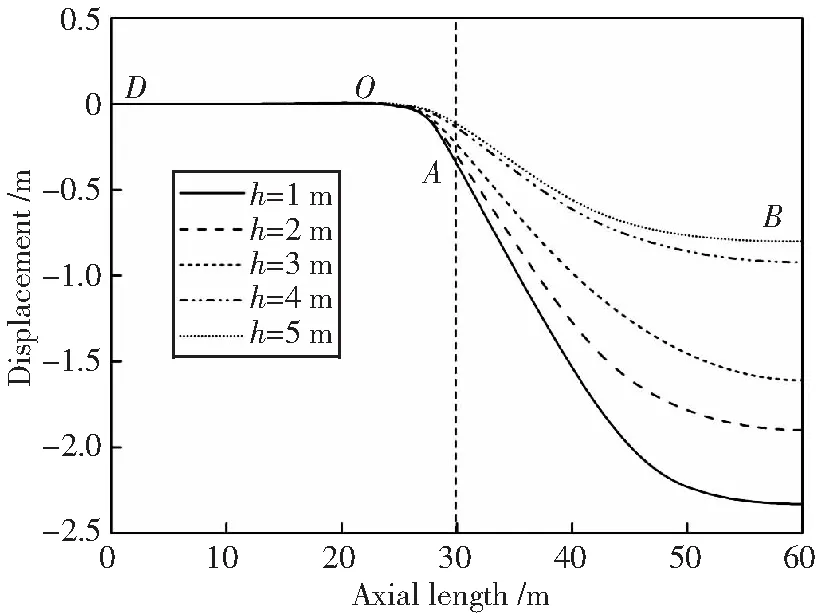
图7　不同埋深管道的挠曲线 (c=24.6 kPa)Fig.7　　　　Deflection curves under different buried depths(c=24.6 kPa)

图8　不同埋深下管道最大轴向应变(c=24.6 kPa)Fig.8　Axial strain under different buried depths (c=24.6 kPa)

当地层沉降量为5 m，围土粘聚力为1 kPa时，不同埋深下管道挠曲线如图9所示。该工况下的埋地管道挠曲变形随埋深的增加而增大；与图7相比，OA管段的长度更长。主要是由于围土的粘聚力较低，管道作用下形成的土拱效应较弱，围土对管道的约束力较小，在埋地管道的作用下，地表面更易出现隆起现象。而埋深越深，管道承受的外载越大，导致管道的挠曲变形越大。

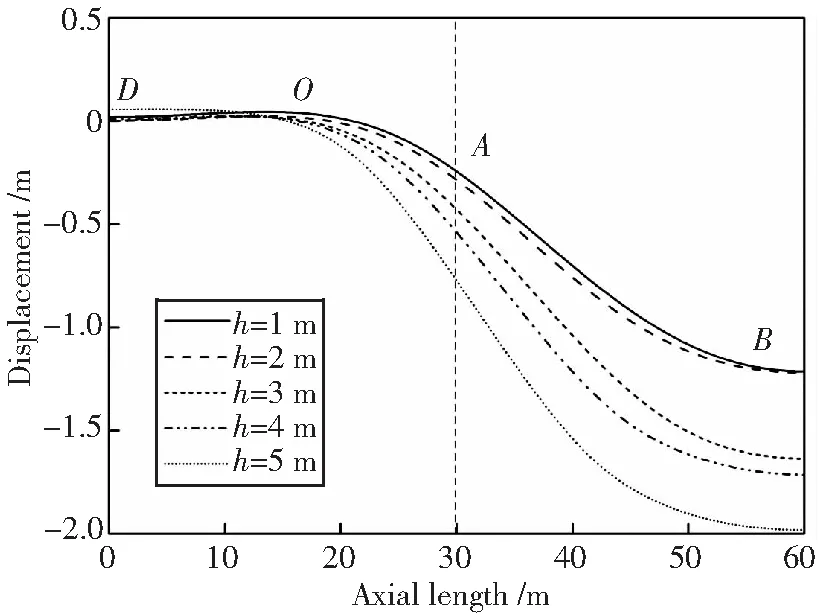
图9　不同埋深管道的挠曲线 (c=1 kPa)Fig.9　Deflection curves under different buried depths (c=1 kPa)

4　土体参数影响分析

4.1　弹性模量

地层塌陷过程中，管土相互作用对埋地管道变形影响较大。地层塌陷量为6 m，不同土体弹性模量下的埋地管道挠曲线如图10所示。不同弹性模量的地层中，OA管段变形较小，而AB管段的位移变化较大。随着土体弹性模量增大，管道位移量逐渐增大。

图10　不同土体弹性模量下的管道挠曲线 Fig.10　Deflection curves under different elasticity modulus of the soil

图11所示为不同土体弹性模量下的管道顶部最大轴向应变。随着土体弹性模量增大，管道轴向应变逐渐增大。当地层沉降量较大时，管道轴向应变变化较为明显，而当沉降量小于2 m时，管道轴向应变较小，且受土体弹性模量影响较小。

4.2　泊松比

图12所示为地层塌陷6 m时不同土体泊松比下的管线挠曲线。土体泊松比对管道位移影响非常小，只有AB段的下半部分出现了较小的变化。图13为不同土体泊松比下管道顶部最大轴向应变。无论是何种地层沉降工况下，管道轴向应变均变化较小，说明了地层土体泊松比对整个塌陷区管道力学性能影响较小。

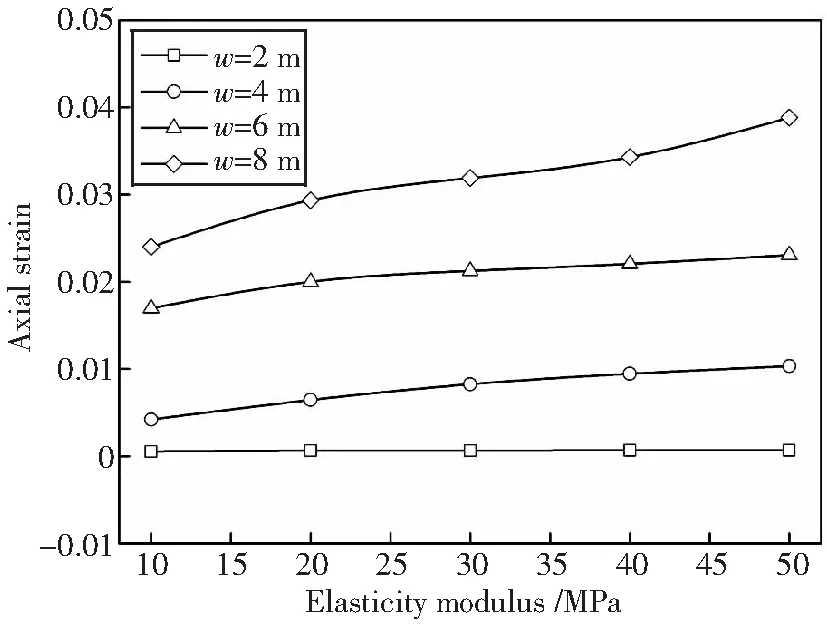
图11　不同土体弹性模量下管道最大轴向应变Fig.11　　　　Axial strain curve under different elasticity modulus of the soil

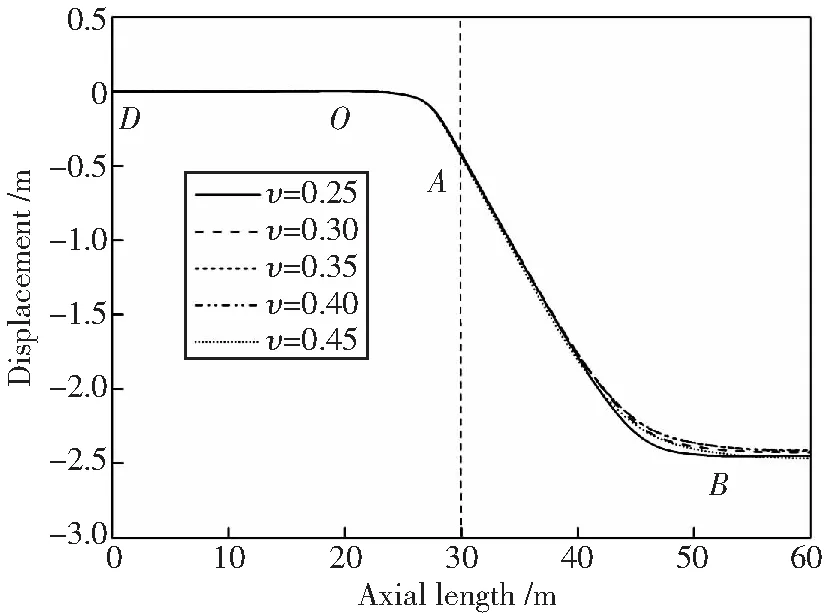
图12　不同土体泊松比下的管道挠曲线Fig.12　Deflection curves under different soil’s Poisson’s ratios

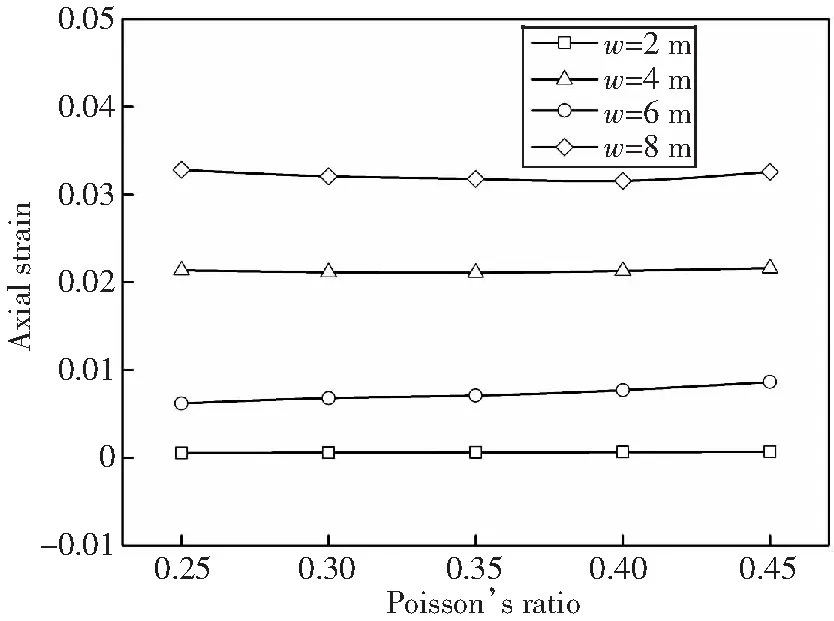
图13　不同土体泊松比下管道最大轴向应变Fig.13　Axial strain under different soil’s Poisson’s ratios

4.3　粘聚力

地层塌陷量为6 m时，不同土体粘聚力下的埋地管道挠曲线如图14所示。随着土体粘聚力的增大，管道位移逐渐增大，主要变化区域是内过渡区和中间塌陷区，而外过渡区的变化较小。说明在相同沉降量下，处于粘聚力较大地层中的埋地管道更容易发生失效。

图15为不同粘聚力土体中的管道顶部最大轴向应变。随着土体粘聚力逐渐增大，管道轴向应变逐渐增大，但是不同地层沉降量下的轴向应变变化规律不同。当沉降量小于2 m时，轴向应变对粘聚力变化较小，而随着土体粘聚力的增大，轴向应变曲线的变化率逐渐增大，且呈非线性规律变化。

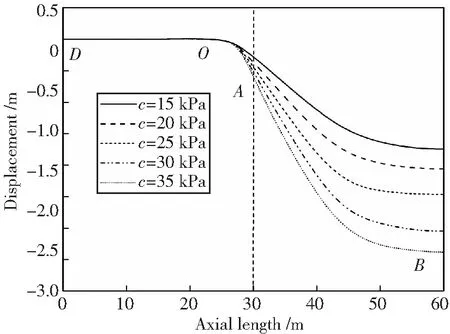
图14　不同土体粘聚力下的管道挠曲线Fig.14　Deflection curves under different soil’s cohesions

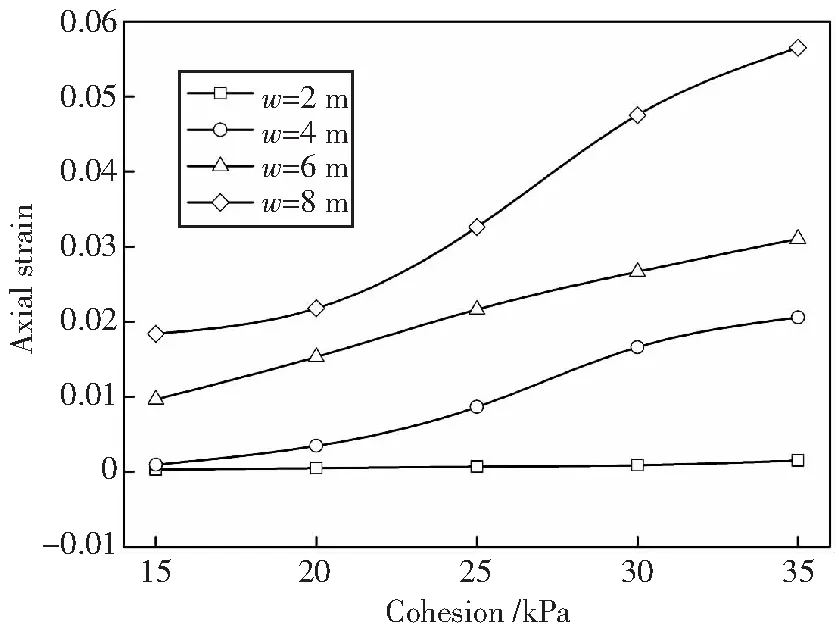
图15　不同土体粘聚力下管道最大轴向应变Fig.15　Axial strain curve under different soil’s cohesions

5　结论

1)随着塌陷量不断增大，管道变形逐渐增大，

且成非线性规律变化；随着壁厚的增大，管道挠曲变形逐渐减小；管道轴向应变随着地层沉降量的增大而增大，随着壁厚的增大而减小；上覆土粘聚力较大时，管道挠曲变形随着埋深的增加而减小；而当上覆土粘聚力较小时，管道挠曲变形随着埋深的增加而增大。

2)地层土体泊松比对管道的变形和应变影响较小；随着土体弹性模量和粘聚力的增大，管道挠曲变形和轴向应变逐渐增大；当塌陷量较小时，土体参数对管道轴向应变影响较小。

[1] 梁政,张杰,韩传军. 地质灾害下油气管道力学[M]. 北京:科学出版社,2016:1-3.

[2] 卫杰. 油气管道事故分析及角莱管道风险评价[D]. 东营:中国石油大学(华东),2006:3-5.

[3] 高惠瑛,冯启民. 场地沉陷埋地管道反应分析方法[J]. 地震工程与工程振动,1997,17(1):68-74.

[4] Ariman T, Muleski G E. A review of the response of buried pipelines under seismic excitations[J]. Earthquake Engineering and Structure Dynamic,1981,9(2):133-151.

[5] 梁政. 石油工程中的若干力学问题[M]. 北京:石油工业出版社,1999:23-27.

[6] 尚尔京,于永南. 地层塌陷区段埋地管道变形与应力分析[J]. 西安石油大学学报:自然科学版,2009,24(4):46-49.

[7] 王晓霖,帅健,张建强. 开采沉陷区埋地管道力学反应分析[J]. 岩土力学,2011,32(11):3373-3378.

[8] Yuan F, Wang L Z, Guo Z, et al. A refined analytical model for landslide or debris flow impact on pipelines-partⅡ：embedded pipelines[J]. Applied Ocean Research,2012,35(1):95-104.

[9] 关惠平,姚安林,谢飞鸿,等. 采空塌陷区管道最大轴向应力计算及统计分析[J]. 天然气工业,2009,29(11):100-103.

[10] 刘爱文. 基于壳模型的埋地管线抗震分析[D]. 北京:中国地震局地球物理研究所,2002:21-25.

[11] 张杰,梁政,韩传军,等. 落石冲击作用下架设油气管道响应分析[J]. 中国安全生产科学技术,2015,11(7):11-17.

[12] Zhang J, Liang Z, Zhang H，et al. Failure analysis of directional crossing pipeline and design of a protective device[J]. Engineering Failure Analysis,2016,66:187-201.

[13] 王树丰,殷跃平,门玉明. 黄土滑坡微型桩抗滑作用现场试验与数值模拟[J]. 水文地质与工程,2010,37(6):22-26.