集装箱笼架结构模态分析

2018-04-02韩伟峰邢海军

机械工程与自动化 2018年1期

韩伟峰，邢海军，张　晗

(石家庄铁道大学机械工程学院，河北　石家庄　050043)

0　引言

集装箱笼架是一种具有一定强度和刚度的用于装载货物的大型框架结构。由于振动会造成机器结构的共振或疲劳从而使结构损坏，且振动与结构自身的固有频率和振型有密切关系，因此了解结构的振动特性才可以对结构进行相应的优化设计。模态分析就是分析结构的振动特性，得到结构的固有频率和振型。本文分析的某公司生产的20尺集装箱笼架为铁路运输中的快速装卸集装箱笼架，笼架结构为由Q345方形钢管焊接的箱型结构[1]，有限元分析方法是此类结构分析的有效方法，故本文应用ANSYS 14.0对集装箱笼架结构进行模态分析计算[2-6]，并提取结构的前10阶模态，分析笼架结构的各阶固有频率与振型，为其优化设计提供依据，以保证结构使用的可靠性。

1　模态分析理论依据

研究结构系统的固有振动特性，首先要建立系统的运动方程，对于一个n自由度线性系统，其运动微分方程为：

(1)

其中：[M]、[C]、[K]分别为系统的质量矩阵、阻尼矩阵、刚度矩阵；{x}、{F}分别为系统各点的位移响应向量与激励向量。

有限元模态分析用于求解机械结构的固有振动特性，由于阻尼对结构模态频率与振型的影响较小，故忽略不计，则系统的无阻尼自由振动方程为：

(2)

在考虑系统的固有振动时，最关心的是系统的同步运动，即系统在各坐标上除了运动幅值不相同外，随时间变化的规律都相同，假设系统的运动为：

x=Φf(t).

(3)

其中：f(t)为运动规律的时间函数；Φ为常数列向量。

将主振动设为：

x=Φsin(ωt+φ).

(4)

其中：Φ=[Φe1Φe2…Φen]T；ω为圆频率；φ为相位角，φ为常数。

将式(4)代入式(2)，得下列代数齐次方程组：

(K-ω2M)Φ=0.

(5)

方程组(5)存在非零解Φ的充分必要条件是系数行列式为零，即：

|K-ω2M|=0.

(6)

式(6)称为系统的特征方程，具体形式为：

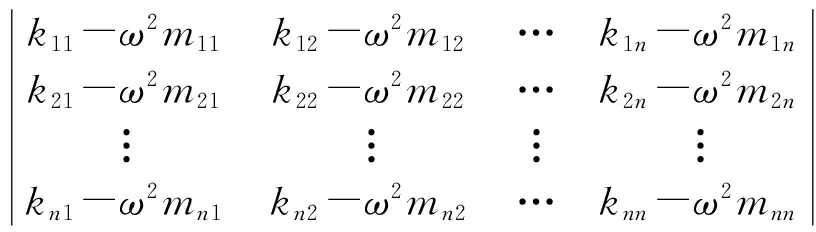
(7)

其中：kij、mij分别为刚度影响系数和质量影响系数。

式(7)展开后是关于ω2的n次代数多项式，称为特征多项式，ω2称为特征根或特征值，由式(7)解出的n个特征值按升序排列为：

2　ANSYS模态分析

模态分析用于确定设计结构的振动特性(固有频率和振型)，它们是承受动载荷的结构设计中的重要参数，同时也是瞬态分析、谐响应分析、谱分析的起点。模态分析是一种线性分析，任何非线性均被忽略。模态分析包括缩减法、子空间迭代法、不对称法、阻尼法、分块兰索斯法、快速动力法。模态分析分的具体步骤如下：

(1) 模型建立：在前处理中定义单元类型、单元常数、材料性质等，定义单元时必须选用线性单元。

(2) 加载及求解：定义模态分析，声明模态分析方法，施加载荷，进行有限元计算求解固有频率。

(3) 扩展模态：将振型写入结果文件。

(4) 观察结果：结果包括固有频率、扩展的振型、相对应力和力的分布。

3　集装箱笼架结构模型分析

3.1　笼架结构分析

集装箱笼架结构为焊接结构，为提高计算效率，减轻工作量，在确保分析结果在误差允许范围的前提下对结构进行了相应的简化。集装箱笼架结构由角柱、上边梁、横梁、小立柱、中边梁、滑轨中横梁、底边梁、端梁、斜撑组成。笼架结构如图1所示。

3.2　有限元模型的建立及单元划分

整体结构按空间结构进行计算，建模时取笼架的弹性模量为206 GPa，泊松比为0.3。根据各子结构的断面尺寸设置单元界面参数。

由有限元法的基本原理可知：单元划分越细越均匀，结果与真实情况越接近，但会提高分析时间及分析成本，对计算机的要求也会相应提高。因此在划分网格时要将有限元模型的单元数量控制在合理的范围内。本文建立笼架的有限元模型时采用了Beam188梁单元和Mass21集中质量单元，笼架的框架为轧制方钢管焊接而成，采用Beam188梁单元建立，除连接处外，网格一律采用四边形，边长为20 mm，内装小集装箱用Mass21建立，通过RBE3命令将Mass21的重力载荷传到笼架的相应安装位置。笼架的有限元模型见图2，X坐标轴为纵向(列车行驶方向)，Y坐标轴为横向，Z坐标轴为垂向。