标准包络环面蜗杆副通用接触线方程及数值求解

吴 彬，张 璐，李昌冉，李 雄，陈旭锋

（长安大学，陕西 西安710064）

0　引言

环面蜗杆传动相对于圆柱蜗杆传动具有啮合齿数多，承载能力大的优点[1]。我国生产的二次包络环面蜗杆主要有平面二次包络环面蜗杆、锥面二次包络环面蜗杆[2]，其广泛应用于机械、化工、冶金等领域[3]。由于包络环面蜗杆副齿廓曲面的复杂性，对其进行齿面方程的求解也很复杂，国内外众多学者对其进行了研究，代表有胡来瑢[4]、董学朱[5]、L.V.Mohan[6]等，都针对性的对环面蜗杆副接触线方程进行了推导，但很少有对二次包络环面蜗杆副通用接触线方程进行推导。本文推导了标准二次包络环面蜗杆副的通用接触线方程，最后以平面二次包络环面蜗杆为例对接触线方程的求解进行了研究。

1　标准二次包络环面蜗杆副通用接触线方程

1.1　坐标系设置

根据蜗杆毛坯与工具齿轮的相对运动关系，为了表达和计算方便，建立如图1所示的蜗杆表面坐标系。

图1　第一次包络坐标系

图中，C为蜗杆副中心距；S0（i0j0k0）为刀座（蜗轮）静坐标；Sw（iwjwkw）为蜗杆静坐标；S1（i1j1k1）和S2（i2j2k2）分别是蜗轮和蜗杆的动坐标系；φ1，φ2为蜗轮、蜗杆在定坐标系转角。

1.2　第一次包络蜗杆齿面上通用接触线方程

S0（i0j0k0）和Sw（iwjwkw）分别是与机架固定连接的刀座和蜗杆上的静坐标，S1（i1j1k1）和S2（i2j2k2）分别是与刀座和蜗杆固接的动坐标系。第一次包络形成蜗杆齿面，成型面上啮合点p在S1中的位置表达式：

啮合点处单位法向量三个分量可表示为：

啮合点处的相对运动速度可由下式求得：

式中 w(12)=w(1)-w(2)=-sinφ1i1-cosφ1j1+i12k1

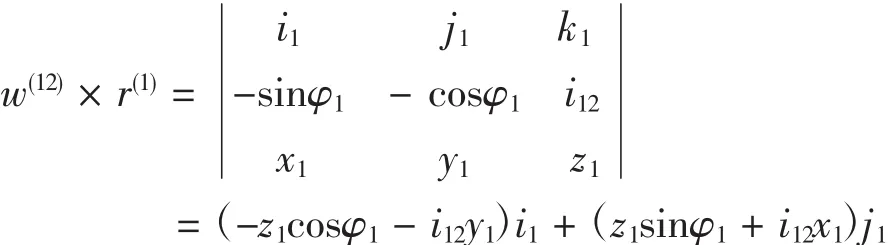
将（4）、（5）代入（3）整理而得

根据共轭理论可知第一次包络啮合函数可表示为：

把（2）、（6）代入（7）整理而得第一次包络通用啮合函数：

其中

通过坐标变换，将动坐标系S1中p1转换到蜗杆动坐标系S2中p2得

联立（1）、（2）、（8）、（9）得到第一次包络蜗杆齿面通用接触线方程。

1.3　第二次包络蜗轮通用接触线方程

如图2是用于获得蜗轮表面坐标，Sg（igjgkg）和Sw（iwjwkw）分别是蜗轮上静坐标和蜗杆上静坐标，S1（i1j1k1）和S2（i2j2k2）分别是蜗轮和滚刀的动坐标系，θ1，θ2为蜗轮、蜗杆在定坐标系转角。第二次包络形成蜗轮齿面Σ1，啮合点处的单位公法线向量与第一次相同。由于单位公法向量为自由向量，只考虑坐标的旋转变换，所以有

图2　第二次包络坐标系

啮合点处的相对运动速度可由下式求得

令w(1)＝1则

把（12）（13）代入（11）得：

据此，根据共轭理论可知第二次包络通用共轭函数为

其中

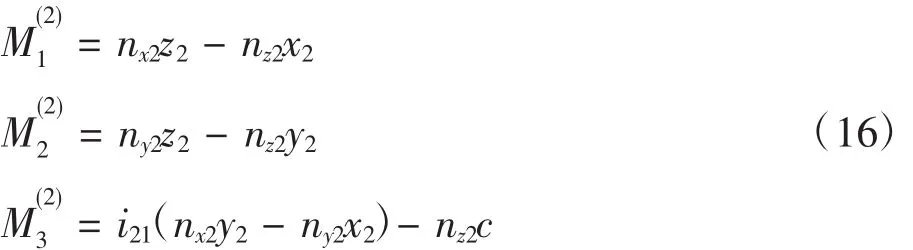
通过坐标变换，将式（15）中 x2、y2、z2用 x1、y1、z1代替得第二次包络通用共轭函数：

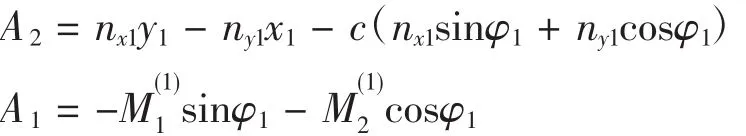
通过坐标变换，将坐标系S2中的p2转换到坐标系S1中p1

联立 （1）、（2）、（8）、（9）、（10）、（16）、（17）、（18）得到第二次包络蜗轮齿面通用接触线方程。

2　平面二次包络环面蜗杆副

2.1　标准平面二次包络环面蜗杆副接触线方程

包络面为平面的环面蜗杆传动，称为平面二次包络环面蜗杆传动，见图3.

图3　成型面坐标系

由（1）可知

由（2）可得

将（18）（19）代入（9）可得

所以将式（21）代入（8）得第一次包络啮合函数为：

把式（18）（19）（20）代入（8）可得

把式（23）代入到（17）可知标准平面二次包络环面蜗杆传动共轭函数为：

联立 （1）、（2）、（8）、（9）、（10）、（16）、（24）、（18）得到平面二次包络蜗轮齿面通用接触线方程。

2.2　数值求解

求解平面二次包络环面蜗杆传动接触线方程关键是求解式（24），由于上面推导的式（24）是关于θ2的非线性三角函数，无法直接求解，因此要对其进行牛顿迭代法求解。由图4可知共轭函数关于转角θ2连续可导，所以可以使用牛顿迭代法进行求解。迭代求解的流程如下：

设θ为式（24）φ(2)=0的根，给定初始值θ=θ2.

将θ2代入如下所示的迭代关系式，求解出新的θ2作为θ的一次近似值。

将θ的一次近似值作为新的θ值，代入迭代关系式得到θ的二次近似值，循环进行。因为共轭函数关于转角θ2连续可导，由Matlab求得共轭函数的导函数如图4所示，可知初始值取60°，此时迭代关系式必定有收敛解。控制结果计算误差为0.001°进行求解，最终完成平面二次包络环面蜗轮齿面接触线求解。

图4　共轭函数连续可导性

已知蜗杆为单头蜗杆，传动比i21=40，模数m=10.03 mm，蜗轮齿顶圆直径为417.36 mm，齿根圆直径为381.24 mm，分度圆直径为401.3 mm；蜗轮齿距角为9°，工作起始角为6°.最后通过Matlab程序计算，在Matlab软件中求得蜗轮齿面上接触线如图5所示。

图5　蜗轮接触线

3　结束语

（1）本文详细推导了标准二次包络环面蜗杆副通用接触线方程，然后以平面二次包络环面蜗杆传动为例验证其正确性，这对推导一般环面蜗杆副接触线方程具有指导意义。

（2）本文采用牛顿迭代法的数值方法求解了接触线方程，并通过实例计算，得到蜗轮接触线图，此数值方法对求解其它超越方程具有参考价值。

参考文献：

[1]郑 亮，费 凌.基于MATLAB滚锥包络环面蜗杆副接触线的求解方法[J].西华大学学报（自然科学版），2008，27（1）：63-65.

[2]段德荣.包络环面蜗杆传动通用啮合函数及其应用[J].太原工业大学学报，1987，1（2）：30-41.

[3]阳 培，王长路.用啮合原理与数值方法求蜗杆副接触线[J].机械传动，2004，1（2）：4-6.

[4]胡来瑢.空间啮合原理及应用（下册）[M].北京：煤炭工业出版社，1986：58-76.

[5]董学朱.环面蜗杆传动设计和修型[M].北京：机械工业出版社，2004：15-30.

[6]L.V.Mohan，M.S.Shunmugam.Geometrical aspects of double enveloping worm gear drive[J].Mechanism and Machine Theo ry，2009，44（11）：2053-2065.