具有Banach代数的无正规的锥度量空间上拟收缩映射的不动点定理的改进*
2018-04-02朴勇杰
朴勇杰
(延边大学理学院数学系,吉林 延吉 133002)
1974年Ciric在完备的度量空间(X,d)上引进了X上的自映射T拟收缩映射的概念:如果存在k∈[0,1)使得对任何x,y∈X,总有
d(Tx,Ty)≤kmax{d(x,y),d(x,Tx),d(y,Ty),
d(x,Ty),d(y,Tx)}
并证明了完备的度量空间上任何拟收缩映射必有唯一不动点。
最近,Kumam等[1]引进了如下概念:称度量空间X上自映射T是推广的拟收缩的,如果存在q∈[0,1)使得对任何x,y∈X,成立
d(Tx,Ty)≤qmax{d(x,y),
d(x,Tx),d(y,Ty),d(x,Ty),
d(y,Tx),d(T2x,x),d(T2x,Tx),
d(T2x,y),d(T2x,Ty)}
文献[1]用实例说明了新的拟收缩概念明显弱于Ciric的拟收缩,并证明当X是T-轨道完备时T具有唯一不动点。因此所得结论明显推广和改进了Ciric的结果。
2007年,Huang等[2]引进了锥度量空间的概念,推广和改进了通常的实空间,并得到若干的不动点定理。特别是近几年,一些作者在锥度量空间上研究了拟收缩映射,得到了若干重要结果[3-7]。
最近, 在文献[8-10]中引进了具有Banach代数的锥度量空间并得到了一些推广的不动点定理, 特别是, Liu等[9]在正规条件下得到了关于拟收缩映射的不动点存在定理。之后, 许绍元等[11]和Huang等[12]分别用两种不同的方式证明了在非正规的条件下文献[9]中得到的结果仍然成立,所得结果具有一定的意义。
在本文,将沿用文献[11-12]中的研究方法并结合文献[1]中的推广的拟收缩条件讨论并得到无正规条件下的新的不动点定理,推广和改进文献[9,11-12]中的相应结果。
1 基本知识
设Α总是实Banach代数,即Α是具有乘法运算的实Banach空间,其运算满足如下性质(对任何x,y,z∈Α,α∈R):
(i) (xy)z=x(yz);
(ii)x(y+z)=xy+xz,(x+y)z=xz+yz;
(iii)α(xy)=(αx)y=x(αy);
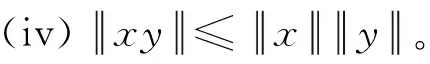
本文总假设Α具有单位元(即乘法单位元)e使得对任何x∈Α均有ex=xe=x。一个元x∈Α被称为可逆的,如果存在称之为逆元的元y∈Α使得yx=xy=e。x的逆元y用x-1表示。详文献[13]。
命题1[13]设Α是具有单位元e的实Banach代数且x∈Α。如果x的谱半径r(x)<1, 即
则(e-x)是可逆的,且有
注1i) 对任何
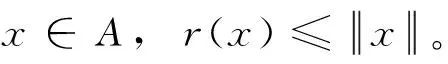
详见文献[13];
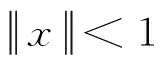
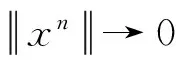
称具有零元0的Banach代数Α的子集P为锥,如果
(i)P是非空闭集且满足{0,e}⊂P;
(ii) 对任何非负实数α,β,αP+βP⊂P;
(iii)P2=PP⊂P;
(iv)P∩(-P)={0}。
对于给定的锥P⊂Α, 定义关于P的半序≤如下:x≤y当且仅当y-x∈P。x 称锥P是正规的是指存在正实数M使得对任何x,y∈Α, 满足上述条件的最小的正数M被称为P的正规常数。 定义1[8-10]设X≠∅。如果映射d:X×X→Α满足 (i)对任何x,y∈X,d(x,y)≥0且d(x,y)=0当且仅当x=y; (ii)对任何x,y∈X,d(x,y)=d(y,x); (iii) 对任何x,y,z∈X,d(x,z)≤d(x,y)+d(y,z)。 则称d是X上的锥度量,(X,d)是具有Banach代数Α的锥度量空间。 注3关于具有Banach代数的锥度量空间的例子可参看文献[8-10]。 定义2[8-10]设(X,d)是具有Banach代数Α的锥度量空间,x∈X且{xn}是X中的序列。 则 (i) 称{xn}收敛于x是指对任何c∈Α且c0,存在自然数N使得对任何n≥N,d(xn,x)≼c。记为或xn→x。 (ii) 称{xn}是柯西的是指任何c∈Α且c0,存在自然数N使得对任何n,m≥N,d(xn,xm)≼c。 (iii) 称(X,d)是完备的是指(X,d)中的每个柯西序列都在(X,d)中收敛。 引理1[14-15]设E是具有体锥P的Banach空间。 若对任何c0,成立0≤u≤c,则u=0。 定义3[16-17]设P是Banach代数Α中的体锥。称序列{un}⊂P为c-序列,如果对任何c0,存在自然数N使得对任何n≥N,un≼c。 命题2[16]设P是Banach代数Α中的体锥,{xn}和{yn}是P中的两个序列。如果{xn}和{yn}都是c-序列且α,β≥0,则{αxn+βyn}也是c-序列。 命题3[16]设P是Banach代数Α中的体锥,{xn}是P中的序列。则下列命题等价: (i) {xn}是c-序列; (ii) 对任何c0,存在自然数N1使得对任何n≥N1时un (iii) 对任何c0,存在自然数N2使得对任何n≥N2时un≤c。 命题4[10]如果P是Banach代数Α中的体锥,k∈P是任意给定的向量且{un}是c-序列,则{kun}也是c-序列。 命题5[10]设(X,d)是具有Banach代数Α的锥度量空间且P是Α中的体锥。 若{xn}是X中收敛于x∈X的序列。 则 (i) {d(xn,x)}是c-序列; (ii)对任何自然数p,{d(xn,xn+p)}也是c-序列; 命题6[10]设Α是Banach代数且x,y∈Α。如果x和y可交换,则r(xy)≤r(x)r(y)。 定义4设(X,d)是具有Banach代数Α的锥度量空间,T:X→X是一个映射。对任何x∈X及正整数n,令 OT(x,n)= {x,Tx,T2x,…,Tnx},OT(x,+∞)= {x,Tx,T2x,…} 称OT(x,+∞)为x点的T-轨道,称(X,d)为T-轨道完备是指OT(x,+∞)中的每个柯西序列必收敛。 注4定义4是文献[1]中相应定义在具有Banach代数Α的锥度量空间上表现形式。 文献[9,11-12]中给出如下定义: 定义5设(X,d)是具有Banach代数Α的锥度量空间。 称一个映射T:X→X为拟收缩的是指存在k∈P且r(k)<1使得对任何x,y∈X,成立 d(Tx,Ty)≤ku (1) 其中u∈{d(x,y),d(x,Tx),d(y,Ty),d(x,Ty),d(y,Tx)}。 文献[11-12]在X的非正规条件下分别给出了如下拟收缩映射的不动点存在定理: 定理1设(X,d)是具有Banach代数Α的完备锥度量空间。如果T:X→X为拟收缩映射,即满足式(1)。则T有唯一不动点,并且对任何x∈X,迭代序列{Tnx}收敛于该不动点。 下面,首先给出如下新的一类拟收缩映射的不动点存在定理。 定理2设(X,d)是具有Banach代数Α的锥度量空间,T:X→X为自映射。如果X是T-轨道完备的且存在k∈P且r(k)<1使得对任何x,y∈X,成立 d(Tx,Ty)≤kv(x,y) (2) 其中v(x,y)∈A(x,y){d(T2x,x),d(T2x,Tx),d(T2x,y),d(T2x,Ty)}。则T有唯一不动点,并且对任何x∈X,迭代序列{Tnx}收敛于该不动点。 证明任取x0x∈X并定义xn=Tnx=Tn-1xn-1,n=1,2,…,构造一个序列对任何固定的i=1,2,…,根据式(2), d(xi,xi+1)=d(Txi-1,Txi)≤kv(xi-1,xi) (3) 其中 v(xi-1,xi)∈A(xi-1,xi)= {d(T2xi-1,xi-1),d(T2xi-1,Txi-1), d(T2xi-1,xi),d(T2xi-1,Txi)} 即v(xi-1,xi)∈A(xi-1,xi)={d(xi+1,xi-1),d(xi+1,xi),0}。 如果v(xi-1,xi)=d(xi+1,xi-1),则根据式(3)得到 d(xi,xi+1)≤kd(xi+1,xi-1) 如果v(xi-1,xi)=d(xi+1,xi),则根据式(3)得到 d(xi,xi+1)≤kd(xi+1,xi)⟹(e-k)d(xi,xi+1)≤0 于是根据命题 1得到 d(xi,xi+1)=0≤kd(xi+1,xi-1) 如果v(xi-1,xi)=0,则根据式(3)得到 d(xi,xi+1)=0≤kd(xi+1,xi-1) 综合上三种情况得到 d(xi,xi+1)≤kd(xi+1,xi-1),i=1,2,… (4) 对任何固定的i=1,2,…,利用式(2), d(xi,xi+2)=d(Txi-1,Txi+1)≤kv(xi-1,xi+1) (5) 其中v(xi-1,xi+1)∈A(xi-1,xi)={d(xi+1,xi-1),d(xi+1,xi),0,d(xi+1,xi+2)}。 若v(xi-1,xi+1)=d(xi+1,xi-1),则根据式(5)得到 d(xi,xi+2)≤kd(xi-1,xi+1) 若v(xi-1,xi+1)=d(xi+1,xi),则根据式(5)和式(4)得到 d(xi,xi+2)≤kd(xi,xi+1)≤k2d(xi-1,xi+1) 若v(xi-1,xi+1)=0,则根据式(5)得到 d(xi,xi+2)≤0≤kd(xi-1,xi+1) 若v(xi-1,xi+1)=d(xi+1,xi+2),则根据式(5)和式(4)得到 d(xi,xi+2)≤kd(xi+1,xi+2)≤k2d(xi,xi+2) 于是 (e-k2)d(xi,xi+2)≤0 根据命题 6可知r(k2)≤(r(k))2<1,于是根据命题 1可知e-k2是可逆的,因此由上式得到 d(xi,xi+2)≤0≤kd(xi-1,xi+1) 综合上述四个情况得到 [d(xi,xi+2)≤kd(xi-1,xi+1)]∨[d(xi,xi+2)≤ k2d(xi-1,xi+1)], ∀i=1,2,… (6) 把式(6)写成 d(xi,xi+2)≤k(i,i+2)d(xi-1,xi+1), ∀i=1,2,… (7) 其中[k(i,i+2)=k]∨[k(i,i+2)=k2]。 下面将证明:对任何自然数n,当两个自然数i,j满足1≤i,j≤n时成立 d(xi,xj)≤k(e-k)-1[d(x0,x1)+d(x1,x2)] (8) 当n=1时i=j=1,于是式(8)显然成立。假设n=m时式(8)成立, 即 d(xi,xj)≤ k(e-k)-1[d(x0,x1)+d(x1,x2)],∀1≤i,j≤m (9) 现设n=m+1。由于当1≤i,j≤m时式(8)成立,于是可设j=m+1,1≤i≤m。 由于 d(xi,xm+1)=d(Txi-1,Txm)≤kv(xi-1,xm) 其中v(xi-1,xm)∈A(xi-1,xm)={d(xi-1,xi+1),d(xi,xi+1),d(xi+1,xm),d(xi+1,xm+1)}。 (I) 考虑i=1的情况。此时v(x0,xm)∈{d(x0,x2),d(x1,x2),d(x2,xm),d(x2,xm+1)}。 1) 当v(x0,xm)=d(x0,x2)时, d(x1,xm+1)≤kd(x0,x2)≤ k[d(x0,x1)+d(x1,x2)]≤ k(e-k)-1[d(x0,x1)+d(x1,x2)] 2) 当v(x0,xm)=d(x1,x2)时, d(x1,xm+1)≤kd(x1,x2)≤ k[d(x0,x1)+d(x1,x2)]≤ k(e-k)-1[d(x0,x1)+d(x1,x2)] 3) 当v(x0,xm)=d(x2,xm)时, d(x1,xm+1)≤kd(x2,xm)≤ k[d(x1,x2)+d(x1,xm)]≤ k[d(x0,x1)+d(x1,x2)]+kd(x1,xm) 结合式(9)得到 d(x1,xm+1)≤k[d(x0,x1)+d(x1,x2)]+ kk(e-k)-1[d(x0,x1)+d(x1,x2)] 即 d(x1,xm+1)≤ k[e+k(e-k)-1][d(x0,x1)+d(x1,x2)]= k(e-k)-1[d(x0,x1)+d(x1,x2)] 4) 当v(x0,xm)=d(x2,xm+1)时, d(x1,xm+1)≤ k[d(x1,x2)+d(x1,xm+1)]≤ k[d(x0,x1)+d(x1,x2)]+kd(x1,xm+1) 于是得到 d(x1,xm+1)≤k(e-k)-1[d(x0,x1)+d(x1,x2)] 综合以上讨论可知当i=1,j=m+1时式(8)成立。 (II) 考虑i=m的情况。此时 d(xm,xm+1)=d(Txm-1,Txm)≤kv(xm-1,xm) 其中v(xm-1,xm)∈A(xm-1,xm)={d(xm-1,xm+1),d(xm,xm+1),0}。 1) 若v(xm-1,xm)=d(xm-1,xm+1),则 d(xm,xm+1)≤kd(xm-1,xm+1)≤ k[d(xm-1,xm)+d(xm,xm+1)] 即 d(xm,xm+1)≤k(e-k)-1d(xm-1,xm) 于是根据式(4)和式(7)得到 d(xm,xm+1)≤k2(e-k)-1d(xm-2,xm)≤ k2(e-k)-1k(m-2,m)k(m-3,m-1)…k(1,3)d(x0,x2)≤ k(e-k)-1[d(x0,x1)+d(x1,x2)] 2) 若v(xm-1,xm)=d(xm,xm+1),则 d(xm,xm+1)≤ kd(xm,xm+1)⟹(e-k)d(xm,xm+1)≤0 于是 d(xm,xm+1)≤k(e-k)-1[d(x0,x1)+d(x1,x2)] 3) 若v(xm-1,xm)=0,则显然成立 d(xm,xm+1)≤k(e-k)-1[d(x0,x1)+d(x1,x2)] 综合上述三种情况可知当i=m,j=m+1时式(8)仍成立。 (III) 考虑2≤i≤m-1的情况。此时,由于i+1≤m,因此当v(xi-1,xm)取A(xi-1,xm)中的元d(xi-1,xi+1),d(xi,xi+1),d(xi+1,xm)之一时根据归纳原理得到 d(xi,xm+1)≤kv(xi-1,xm)≤ k2(e-k)-1[d(x0,x1)+d(x1,x2)] 而当v(xi-1,xm)=d(xi+1,xm+1)时 d(xi,xm+1)≤kd(xi+1,xm+1)≤ k[d(xi,xi+1)+d(xi,xm+1)] 于是得到 d(xi,xm+1)≤k(e-k)-1d(xi,xi+1) 因此根据式(4)和式(7)得到 d(xi,xm+1)≤k2(e-k)-1d(xi-1,xi+1)≤ k2(e-k)-1k(i-1,i+1)k(i-2,i)…k(1,3)d(x0,x2)≤ k(e-k)-1d(x0,x2)≤ k(e-k)-1[d(x0,x1)+d(x1,x2)] 综合上述讨论可知当2≤i≤m-1,j=m+1时(8)仍然成立。 于是综合所有情况并根据归纳法知式(8)成立。 对任何两个自然数n,m且1 d(xn,xm)=d(Txn-1,Txm-1)≤kv(xn-1,xm-1) 其中v(xn-1,xm-1)∈A(xn-1,xm-1)={d(xn-1,xn+1),d(xn,xn+1),d(xn+1,xm-1),d(xn+1,xm)}。 令 C(n,m)={d(xi,xj)|n≤i,j≤m} 则由上式可知对每个u∈C(n,m),存在v∈C(n-1,m)使得u≤kv。于是得到 d(xn,xm)≤ku1≤k2u2≤…≤ kn-1un-1≤kn(e-k)-1[d(x0,x1)+d(x1,x2)] (10) 其中 u1∈C(n-1,m), u2∈C(n-2,m),…,un-1∈C(1,m) 及 un-1≤k(e-k)-1[d(x0,x1)+d(x1,x2)] (根据式(8)) 由于 kn(e-k)-1[d(x0,x1)+d(x1,x2)]≼c 于是结合式(10)得到对任何c0,存在自然数N>1使得m≥n>N时d(xn,xm)≼c。因此{xn}是OT(x,+∞)中的柯西序列,所以根据T-轨道完备性存在x*∈X使得xn→x*。 根据式(2), 对任何自然数n, d(x*,Tx*)≤ d(x*,xn)+d(Txn-1,Tx*)≤ d(x*,xn)+kv(xn-1,x*) (11) 其中v(xn-1,x*)∈A(xn-1,x*)={d(xn-1,xn+1),d(xn,xn+1),d(xn+1,x*),d(xn+1,Tx*)}。 1) 若v(xn-1,x*)=d(xn-1,xn+1),则根据式(11)得到 d(x*,Tx*)≤d(x*,xn)+kd(xn-1,xn+1) (12) 2) 若v(xn-1,x*)=d(xn,xn+1), 则根据式(11)得到 d(x*,Tx*)≤d(x*,xn)+kd(xn,xn+1) (13) 3) 若v(xn-1,x*)=d(xn+1,x*), 则根据式(11)得到 d(x*,Tx*)≤d(x*,xn)+kd(xn+1,x*) (14) 4) 若v(xn-1,x*)=d(xn+1,Tx*), 则根据式(11)得到 d(x*,Tx*)≤d(x*,xn)+kd(xn+1,Tx*)≤ d(x*,xn)+k[d(xn+1,x*)+d(x*,Tx*)] 于是得到 d(x*,Tx*)≤ (e-k)-1[d(x*,xn)+k[d(xn+1,x*)] (15) 因此综合四种情况可知无论何种,由命题2-命题5,都有 d(x*,Tx*)≤yn 其中{yn}是锥P中的c-序列。于是根据定义3,对任何c0,存在自然数N使得当n>N时d(x*,Tx*)≤yn≼c,因此根据引理 1得到d(x*,Tx*)=0,故x*是T的不动点。 如果y*也是T的不动点,则根据式(2)得到 d(x*,y*)=d(Tx*,Ty*)≤kv(x*,y*) 其中v(x*,y*)∈A(x*,y*)={d(x*,y*),0}。于是容易得到x*=y*,因此x*是T的唯一不动点。 记 B(x,y)= {d(x,y),d(x,Tx),d(y,Ty),d(x,Ty),d(y,Tx)}; D(x,y)= {d(x,y),d(x,Tx),d(y,Ty),d(x,Ty),d(y,Tx), d(T2x,x),d(T2x,Tx),d(T2x,y),d(T2x,Ty)} 则D(x,y)=A(x,y)∪B(x,y)。 注5用(X,d)的T-轨道完备性代替定理 1中的(X,d)的完备性,定理 1仍然成立。 注6定理1的证明的关键一步是:对任何自然数n,当两个自然数i,j满足1≤i,j≤n时成立d(xi,xj)≤k(e-k)-1d(x0,x1)(详见文献[11-12]中的证明),但是这结果也满足式(8)。 结合定理1和定理2并根据注5和注6, 得到如下具有Banach代数的非正规的锥度量空间上Ciric定理(即定理1)的推广结果。 定理3设(X,d)是具有Banach代数Α的锥度量空间,T:X→X为自映射。如果X是T-轨道完备的且存在k∈P且r(k)<1使得对任何x,y∈X,成立 d(Tx,Ty)≤kv(x,y) (2) 其中v(x,y)∈D(x,y)。则T有唯一不动点,并且对任何x∈X,迭代序列{Tnx}收敛于该不动点。 参考文献: [1]KUMAM P, VAN D, SITTHAKERNGKIET K. A generalization of Ciric fixed point theorems [J]. Filomat, 2015, 29(7): 1549-1556. [2]HUANG L G, ZHANG X. Cone metric spaces and fixed point theorems of contractive mappings [J]. J Math Anal Appl, 2007, 332(2): 1468-1476. [3]AI-KHALEEL M, AI-SHARIFA S, KHANDAQJI M. Fixed points for contraction mappings in generalized cone metric spaces [J]. Jordan J Math Stat, 2012, 5(4): 291-307. [4]GAJIC J L, RAKOCEVIC V. Quasi-contractions on a non-normal cone metric spaces [J]. Funct Anal Appl, 2012, 46(1): 75-79. [5]ILIC D, RAKOCEVIC V. Quasi-contractions on a cone metric spaces [J]. Appl Math Lett, 2009, 22(5): 728-731. [6]KADELBURG Z, REDENOVIC S, RAKOCEVIC V. Remarks on “ Quasi-contractions on a cone metric spaces” [J]. Appl Math Lett, 2009, 22(11): 1674-1679. [7]KADELBURG Z, PAVLOVIC M, REDENOVIC S. Common fixed point theorems for ordered contractions and quasi-contractions in ordered cone metric spaces [J]. Comput Math Appl, 2010, 59(9): 3148-3159. [8]LIU H, XU S Y. Cone metric spaces with Banach algebras and fixed point theorems of generalized Lipschitz mappings [J]. Fixed Point Theory and Applications, 2013, 2013(1): 1-10. [9]LIU H, XU S Y. Fixed point theorems of quasi-contractions on cone metric spaces with Banach algebras [J]. Abstr Appl Anal, 2013, 2013(4): 764-787. [10]XU S Y, REDENOVIC S. Fixed point theroems of generalized Lipschitz mappings on cone metric spaces over Banach algebras without assumption of normality [J]. Fixed Point Theory and Applications, 2014, 2014(1): 1-12. [11]许绍元, 马超, 周作领. 具有Banach代数的锥度量空间上拟压缩映射的新的不动点定理[J]. 中山大学学报(自然科学版), 2015, 54(4): 1-4. XU S Y, MA C, ZHOU Z L. A new fixed point theorem of quasi-contractions on cone metric spaces over Banach algebras [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2015, 54(4): 1-4. [12]HUANG H P, XU S Y, LIU H. Fixed point theorems of quasi-contractions on non-normal cone metric spaces with Banach Algebras [J]. Mathematical Applicata, 2015, 28(1): 110-114. [13]RUDIN W. Functional Analysis [M]. 2nd ed. New York: McGeaw-Hill, 1991. [14]REDENOVIC S, RHOADES B E. Fixed point theorem for two non-self mappings in cone metric spaces [J]. Comput Math Appl, 2009, 57(10): 1701-1707. [15]JANKOVIC S, KADELBURG Z, REDENOVIC S. On cone metric space: A survey [J]. Nonl Anal, 2011, 74(7): 2591-2601. [16]KADELBURG Z, REDENOVIC S. A note on various types of cones and fixed point results in cone metric spaces [J]. Asian Journal of Mathematics and Applications, 2013, Article ID ama 0104. [17]DORDEVIC M, DIRIC D, KADELBURG Z, et al. Fixed point results under c-distance in tvs-cone metric spaces [J]. Fixed Point Theory and Applications, 2011, 2011(1): 1-9.
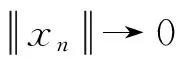
2 拟收缩映射的不动点定理的推广

