基于数学模型的低压配电系统节电器的研究与应用

喻明江 董 勤 冯万兴 周 盛 熊佳俊

（国网电力科学研究院武汉南瑞有限责任公司，武汉 430074）

随着社会经济飞速发展，三相不平衡负荷和非线性负荷也逐渐增多，城市低压配电网中的三相四线制低压配电系统广泛存在三相负荷不平衡以及谐波污染的现象，使城市低压配电网中性线电发热损耗增加，甚至会导致发生火灾。谐波造成的谐波损耗使配电变压器局部严重过热，危害设备绝缘，降低了配用电设备的效率[1-2]。针对以上问题，市场上已出现多种基于不同原理的滤波方案，主要包括并联电力电容器、串联电力电抗器、并联有源电力滤波器和并联低压配电系统节电器等。鉴于低压配电系统节电器具有滤波效果好，无谐振等优点而广泛受到关注[3-4]。基于多绕组磁链耦合的原理，本文介绍了一种低压配电系统节电器的等效数学模型，运用数值计算方法，证明了低压配电系统节电器既可滤除三相不平衡负载的零序电流，又能减小因电源侧三相不平衡电压的零序电压分量产生的零序电流。

1 低压配电系统节电器结构特点

图1为低压配电系统节电器的多绕组绕线方式，每一相绕组线圈包括3个线圈绕组，前两个绕组线圈同向绕制，第三绕组与前两绕组反向绕制，3个线圈绕组分别缠绕在两个磁柱上，A、B、C端子为低压配电系统节电器电源输入端，a、b、c端子为低压配电系统节电器电源输出端，A1、B1、C1第一绕组缠绕的匝数为 N1，A2、B2、C2第二绕组和A3、B3、C3第三绕组缠绕的匝数均为 N2。N1与N2匝数比有这样的数学关系：有 N1远小于 N2。A1、B1、C1绕组和A2、B2、C2绕组的绕向相同，A3、B3、C3绕组的绕向与 A2、B2、C2绕组绕向相反，低压配电系统节电器接入三相四线制低压配电系统方式如图2所示，低压配电系统节电器在电源侧和负荷侧之间实现了并联的零序低阻通道，将负荷产生的基波不平衡、谐波电流等零序电流导入，避免了因三相不平衡负荷和非线性负荷产生的零序电流主要成分流向城市三相四线制配电网，达到了滤波的效果，减小了城市三相四线制配电网中性线的零序电流。由于低压配电系统节电器第一绕组的存在，针对零序电流可等效串联了高阻的零序阻抗，降低了因电源侧三相不平衡电压的零序电压分量产生的零序电流。

图1 节电器接线方式

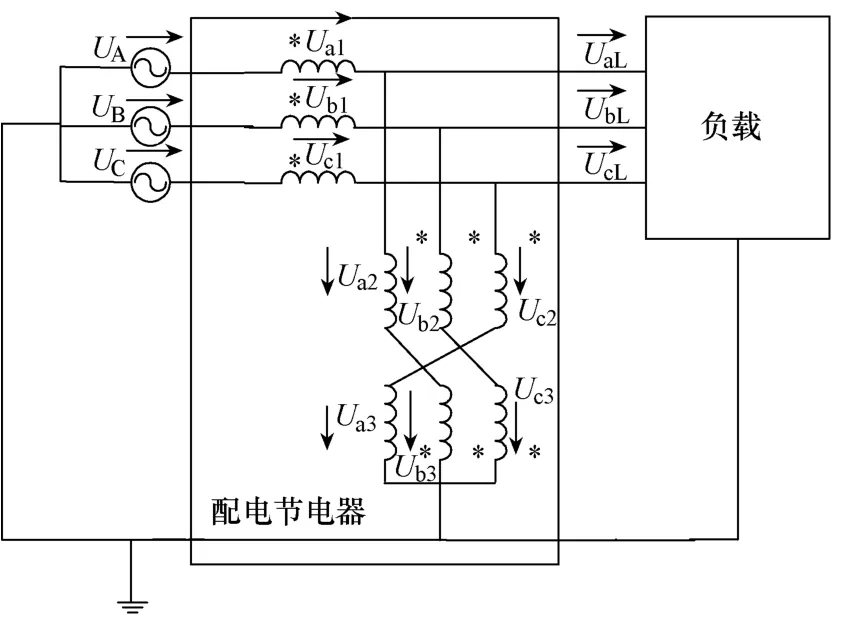
图2 节电器接入方式

实现低压配电系统节电器滤波功能不需要投切电力电容器件，不存在负载谐波被放大的问题，低压配电系统节电器具有适用领域较广、使用便捷、免维护、成本低、安全可靠的优点。

2 低压配电系统节电器数学模型

参照图1所示低压配电系统节电器各矢量参考方向，假设ω 为电力系统的角频率，λ 为低压配电系统节电器内部磁路的磁导，令 jλ=A ，jωN1N2λ=B ，λ= C ，低压配电系统节电器三相线圈第一绕组电阻为 r1，同向缠绕的第二绕组电阻为r2，反向缠绕的第三绕组电阻为r3，并且r2=r3，忽略漏磁， α = ej120o，根据多绕组磁链耦合原理，低压配电系统节电器第一绕组的电压方程可表示为

根据相量对称分量法，将低压配电系统节电器绕组A1、B1、C1电压的正序、负序、零序分量可表示为

将式（1）代入式（2）可有

以上同样可得，低压配电系统节电器第二绕组电压的正序、负序、零序分量为

低压配电系统节电器第三绕组电压的正序、负序、零序分量为

根据式（3）至式（5）可得，低压配电系统节电器各绕组零序电压分量为

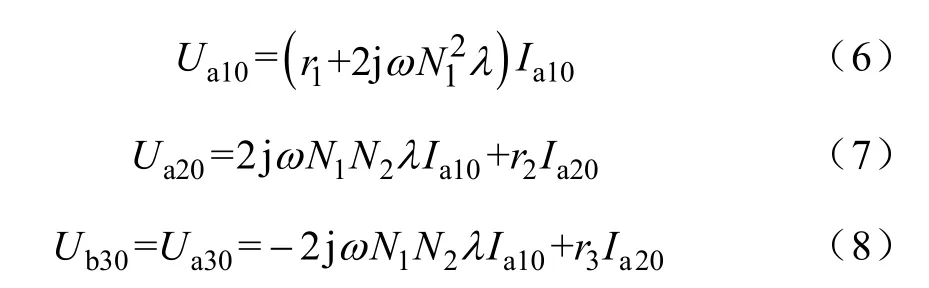
根据式（6）至式（8），图2的零序等效电路如图 3所示。图中sZ为配电系统的等效阻抗，sNZ′为中性线的等效阻抗， ZRN= r2+ r3，ZR= ( r1+ 2jω L1)为低压配电系统节电器的等效零序阻抗；iL0为负荷侧因三相不平衡负荷和非线性负荷产生的等效零序电流源，Us0为城市低压配电系统电源侧因三相电源不平衡时产生的等效零序电压源。

图3 零序等效电路

根据电路叠加原理，可以计算系统中性线的零序电流。先只考虑L0i对系统中性线产生的零序电流，将s0u 电压源短路，得到

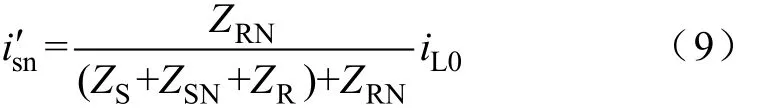
由于 ZRN= r2+ r3，分子数值很小且远小于式（9）中的分母数值，由三相不平衡负荷产生的零序谐波电流 iL0注入系统侧的零序谐波电流值将会受到限制而减小。

再考虑 us0电压对系统中性线零序电流的影响，将 iL0电流源开路，只考虑 us0对负载系统的中性线产生的零序电流。得到

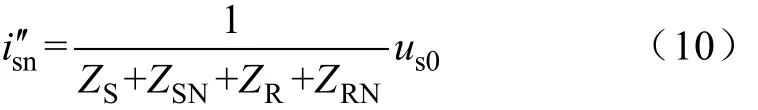
等效阻抗 ZR= r1+ 2jωL1，数值较大，配电系统电源侧产生的零序电压在中性线上产生的零序电流也将受到限制而减小。

经过上述分析，is′n+is′n为系统中性线总的零序谐波电流，由于低压配电系统节电器的接入，所以流入系统的零序谐波电流值将受到限制。

假设 Ra、Rb、Rc为低压配电系统节电器 ABC三相负载电阻。UA、UB、UC为低压配电系统节电器 ABC三相电源，Ua1、Ub1、Uc1为低压配电系统节电器第一绕组的 ABC三相电压，Ua2、Ub2、Uc2为低压配电系统节电器第二绕组的ABC三相电压，Ua3、Ub3、Uc3为低压配电系统节电器第三绕组的ABC三相电压，Ia1、Ib1、Ic1为低压配电系统节电器第一绕组的ABC三相电流，Ia2、Ib2、Ic2为低压配电系统节电器第二绕组的ABC三相电流，Ic2、Ia2、Ib2为低压配电系统节电器第三绕组的ABC三相电流，漏磁忽略不计。根据基尔霍夫电压原理，可以建立低压配电系统节电器6个KVL回路电压方程[5]：

将该方程组整理成为两个矩阵相乘的形式，即U= MI+NpI。其中I为1× 6的列矩阵，其所有元素均为方程组中的未知数，M同样为1× 6列矩阵，其所有元素均为方程组等号右边的数值，均为已知数。本文就得到了一个6× 6的矩阵N，即

式（12）可由数值计算方法龙格库塔法求解。

3 数学方法验证

3.1 平衡线性负载的仿真分析

在Matlab/Simulink软件中设置低压配电系统节电器三相平衡线性负载电阻为

三相进线电感参数为

图4为在Simulink中的三相电流仿真波形。图5为用4/5阶龙格库塔法求解的电流波形[6]。

图4 仿真结果

图5 矩阵计算结果

从图4和图5可以看出，低压配电系统节电器负载侧三相电流对称，矩阵计算结果与仿真结果一致。

3.2 三相不平衡度抑制分析

当三相负荷为不平衡线性负载时，在 Matlab/Simulink软件中加装有低压配电系统节电器条件下，软件中设置三相不平衡电阻为 Ra=2Ω，Rb=5Ω，Rc=5Ω，三相进线电感参数为 La=Lb= Lc=0.0003H。图6为加装低压配电系统节电器第一、二绕组三相电流波和中性线流过的电流仿真结果。图7为低压配电系统节电器用 4/5阶龙格库塔法计算的第一、二绕组三相电流波形[7-8]。

图6 电流仿真结果及局部放大效果图

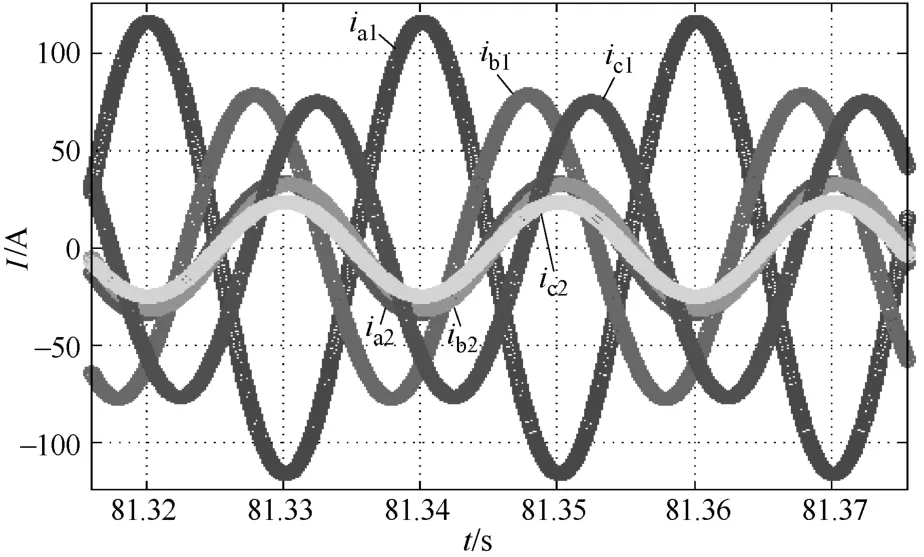
图7 龙格库塔法计算结果

从图6和图7看出，低压配电系统节电器具有平衡不平衡负载的作用。图6和图7可知：低压配电系统节电器的矩阵计算结果与仿真结果一致，矩阵计算方法可靠。证明了低压配电系统节电器具有平衡不平衡负载的功能。

3.3 电源电压不平衡时的仿真结果

电源为正序、负序和零序的组合：

在Matlab/Simulink软件中设置三相不平衡电源为

电压源含有正序、负序和谐波源，在 Simulink仿真结果如图8所示，在Matlab软件中用4/5阶龙格库塔法计算结果如图9所示。

图8 Simulink仿真结果

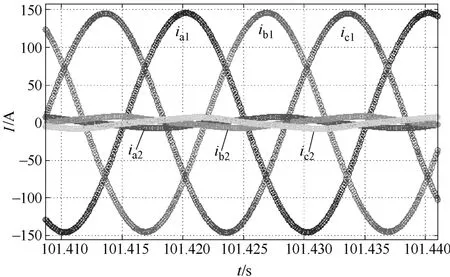
图9 龙格库塔法计算结果

从图8和图9可知，电压源出现负序和零序电压源时，低压配电系统节电器一次侧三相电流畸变比较小，节电器二次侧绕组上面流过畸变电流，仿真和数学计算结果表明低压配电系统节电器具有抑制电压不平衡的功能。

4 实际应用

根据本文的数学模型笔者研制了一台低压配电系统节电器，样机运行结果如图10所示，安装低压配电系统节电器后，电流不平衡度由 3.85%降到3.46%，电流谐波含量由4.13%降至3.40%。

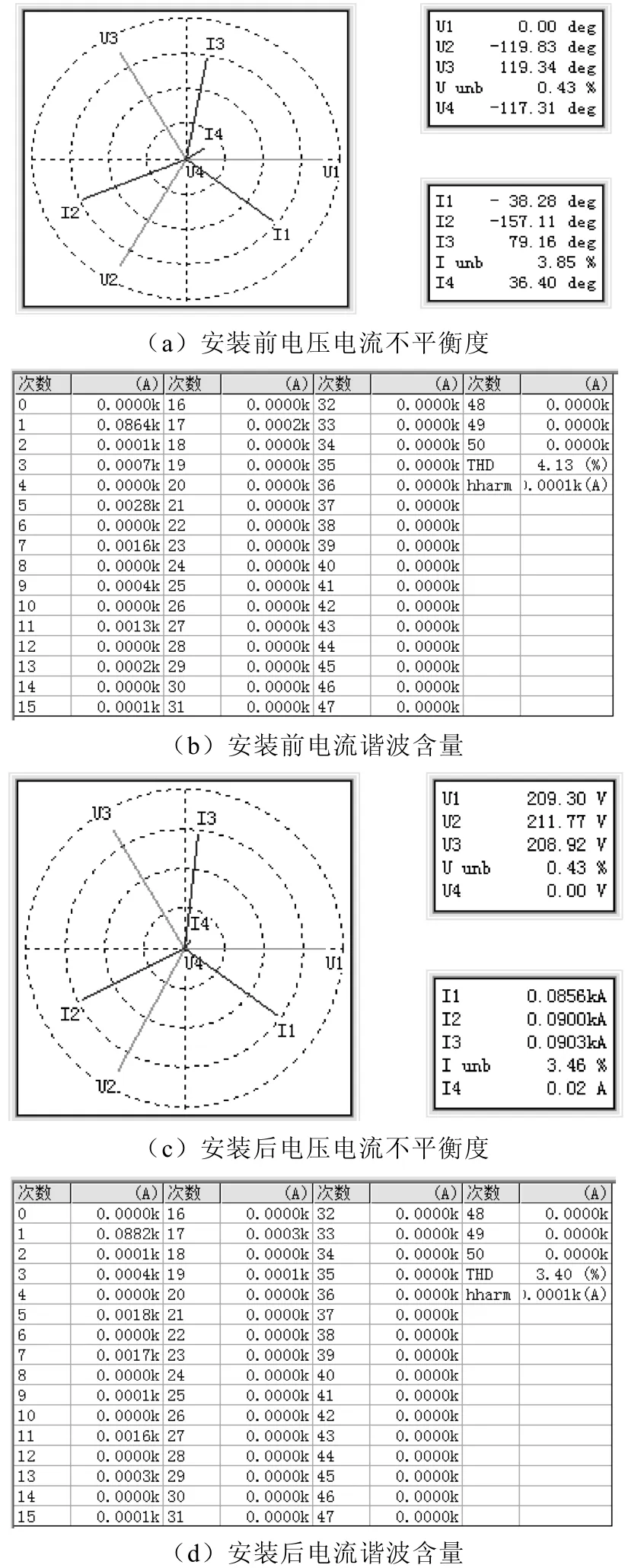
图10 应用结果

5 结论

用Simulink仿真结果和矩阵计算结果对比可以得出如下的结论：矩阵分析计算方法是正确合理的。工程应用结果表明，使用低压配电系统节电器后，在电源侧和负载之间构成了零序低阻旁路，可将负荷产生的基波不平衡、三倍频高次谐波电流等零序电流导入，而不会流入电源侧配电网，达到了滤波节电的效果，低压配电系统节电器具有滤除谐波、平衡三相不平衡负载，抑制电网不平衡电压的作用。

[1] 林志雄, 陈岩, 蔡金锭, 等. 低压配电网三相不平衡运行的影响及治理措施[J]. 电力科学与技术学报,2009, 24(3): 63-67.

[2] 杨云龙, 王凤清. 配电变压器三相不平衡运行带来的附加损耗、电压偏差及补偿方法[J]. 电网技术,2004, 28(8): 73-76.

[3] 李国栋, 冯力鸿, 顾强, 等. 曲折接线变压器抑制零序三次谐波电流方法研究[J]. 现代电力, 2006, 23(6):40-44.

[4] 祝亚峰, 刘飞, 付念先. 配电系统节电器节电技术研究[J]. 能源与节能, 2013, 88(1): 28-31.

[5] 莫青, 刘飞, 喻明江, 等. 基于曲折型自耦变压器的节电器稳态模型[J]. 信息技术, 2014, 4(4): 100-103.

[6] 陶毅, 翟克俊. 低压配电降压节电器技术性能的研究[J]. 节能与环保, 2005, 1(7): 34-35.

[7] 张德丰. Matlab数值计算方法[M]. 北京: 机械工业出版社, 2010.

[8] 张静. Matlab在控制系统中的应用[M]. 北京: 电子工业出版社, 2007.