基于迭代学习控制的肘关节功能性电刺激系统
2018-03-30陈盛勤李玉榕陈建国
陈盛勤 李玉榕 陈 军 陈建国
(1. 福州大学电气工程与自动化学院,福州 350116;2. 福州大学福建省医疗器械和医药技术重点实验室,福州 350116)
肢体功能障碍患者由于大脑或神经系统损伤导致肢体无法受思维控制完成期望动作,严重影响患者的日常生活,给家庭和社会带来严重负担。造成肢体功能障碍的两大疾病脑卒中与脊髓损伤,随着人口老龄化以及交通事故的增多,发病率不断上升。根据我国2016年脑卒中流行病学报告显示,每年新增脑卒中患者200万人,死亡人数165万,存活的患者600~700万人中有3/4的患者有不同程度的肢体功能障碍[1-2]。我国每年脊髓损伤的人数已经达到数十万人。目前没有关于全球患病率的可靠估计,但每年的全球发生率估计为每百万人40至80例[3]。对于如此庞大的肢体功能障碍病人群体,帮助他们肢体运动功能康复的研究是十分有意义的。在肢体运动功能中,上肢功能包括取物、抓物和操作物体,负担着进食、穿衣、洗漱等基本生活技能。上肢运动功能的重建是肢体功能障碍患者实现生活自理的关键。肘关节的康复对整个上肢运动功能的康复是至关重要的。功能性电刺激(functional electrical stimulation, FES)是治疗肢体功能障碍患者四肢运动功能不全的重要康复治疗技术之一,1961年由美国医生Liberson首次提出,并定义为“对肌肉提供电流刺激,在刺激的瞬时产生肌肉收缩,达到移动、抓握或其他肌肉动作[4]。FES技术在改善肢体功能障碍患者的运动功能起到重要作用,经过实验研究与临床治疗验证,FES治疗能有效地提高患者的运动表现[5-6]。设计针对肘关节康复训练的FES系统,对于帮助肢体功能障碍患者的上肢运动功能康复具有重要意义。
针对人体关节运动控制的FES系统研究,国内外已有许多学者投入当中。FES系统的发展是从简单的开环系统结构到闭环系统结构。功能性电刺激开环控制方式,指的是通常通过外部手动控制开关,或者通过压力、加速度等传感器触发FES系统启动或停止[7]。例如Nathan等人研发的HandMaster系统,其通过外部开关调节和控制刺激电流来帮助患者实现手部抓握功能[8]。Shimada等人使用加速度传感器检测足下垂患者的步态,用加速度信号触发电刺激仪器产生指定刺激电流来校正足下垂患者的步态[9]。在这些开环控制系统中,功能性电刺激输出的刺激参数,包括刺激幅值、频率、波形等是固定的,刺激参数依赖于康复指导师的经验设置,采用固定的脉冲序列进行刺激,这样的方式要么产生多余的刺激量导致肌肉疲劳,要么刺激量不足难以使肌肉产生相应的收缩来完成规定的训练运动。可见,开环控制的功能性电刺激系统难以达到理想的康复效果。为实现刺激量的精确调节,产生了功能性电刺激系统的闭环控制方式,包括测量患者康复过程中的轨迹、角度、角速度、关节力矩等参数构成闭环控制系统,实现系统输出参数的精确控制。例如学者Qiu Shuang设计的针对膝关节控制的FES系统,其利用角度反馈,使用基于神经网络与遗传算法的PID算法进行控制,实现闭环控制的FES系统[10]。Lew等人使用一组陀螺仪用于检测手臂运动作,将位置信息反馈,实现闭环控制的FES系统,且使患者实现取物、放物等基本功能任务[11]。相比于国外,国内对FES系统的研究起步较晚,发展较慢,国内更多的学者对下肢的FES系统进行研究,主要在步态校正、膝关节运动、人体站立、以及闭环的 FES脚踏车康复系统等研究领域,对上肢的康复训练的FES系统研究相对较少。控制算法的应用更多是采用传统的PID控制算法与改进的PID控制算法。而肢体康复训练动作常具有重复性,ILC算法相比于PID控制算法更适用于控制重复轨迹跟踪的系统,且ILC算法具有一定的学习能力,抵抗模型参数改变和系统外部噪声的抗干扰能力更强[12-13]。
本文针对肘关节在电刺激下的运动特性,采用神经网络的方法建立电刺激量与肘关节运动角度的模型关系。结合所建模型,用肘关节角度信号进行反馈,用ILC算法控制电刺激量,实现电刺激肘关节运动的闭环控制FES系统。
1 肘关节模型
1.1 建模方法
人工神经网络是一种模仿人脑结构及其功能的信息处理系统。它从信息处理角度对人脑神经元网络进行抽象,按照不同的连接方式组成不同的网络模型。电刺激下肘关节的运动具有时变性和非线性等复杂特性,简单的前馈神经网络无法建立电刺激量与关节角度的模型关系。设计如图1所示,具有反馈与前馈环节的动态神经网络用于建立模型关系。该神经网络由两部分组成:①静态非线性部分,为单隐含层的前馈神经网络;②动态线性部分,为带有前馈迟滞环节和反馈迟滞环节的单层神经网络。图1中u(k)表示输入信号,x(k)表示中间信号,y(k)表示输出信号。Z-1表示单位延时,上标N表示延迟阶数,在本模型中取值为3,下标M表示隐含层神经元个数,在本模型中取值为10。L1、L2和L3为线性神经元,其功能函数为f(x)=ωx+β。S1、S2…SM为 S型神经元,其功能函数为 g(x)=(1−e−x)/(1+e−x)。根据网络的连接关系得到如下模型关系表达式,即
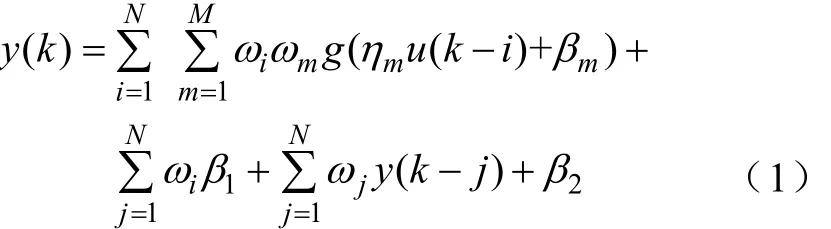
式中,ηm、ωm、ωi、ωj分别为各层连接权,βm、β1和β2分别为各层阈值(m=1,2,…,M;i=1,2,…,N;j=1,2,…,N)。这些模型参数需通过实验数据训练神经网络来确定。对于本文采用的带有反馈和前馈环节的动态神经网络,若采用反向误差传播的方法训练,则训练过程中难以计算出更新误差的梯度信息,使算法难以收敛[14-15]。而神经网络的训练问题实质上可以转化为权值、阈值的优化问题[16]。因此,本文的神经网络模型采用智能优化算法遗传算法进行训练,以确定模型的权值、阈值参数。
通过搭建如图 2所示实验平台进行电刺激实验。功能性电刺激仪器输出的正负极电极片A和B贴被放于肱二头肌上下两端,弯曲型角度传感器被放置于肘关节处。以肘关节为轴心建立直角坐标系,前臂自然下垂时为Y轴负方向,定为起始0°。依次逆时针旋转X轴正方向为90°,Y轴正方向为180°。正常人体肘关节运动范围在0°~135°之间。肘关节在刺激电流与重力作用下在矢状面作屈和伸运动,记录刺激电流与肘关节弯曲角度数据。实验对象为一名 26岁健康男性,身高为 170cm,体重为60kg。实验要求实验者在电刺激过程中不能有主观的运动意识参与,上肢处于完全自由放松状态。健康人在完全放松状态下无意识参与的电刺激运动与肢体功能障碍患者在刺激电流下的运动相同。通过调节电流脉宽的方式调节刺激电流大小。单个刺激脉冲为矩形双相脉冲。刺激电流参数设置如下:周期为0.05s,幅值为30mA,脉宽在40~110μs之间随机波动变化。电刺激仪器为恒流输出,一次电刺激时间设为 30s,为减少单次实验的特异性,将 3次实验数据平均得到一组电刺激量与角度变化的数据,需采集10组数据用于神经网络模型的训练。
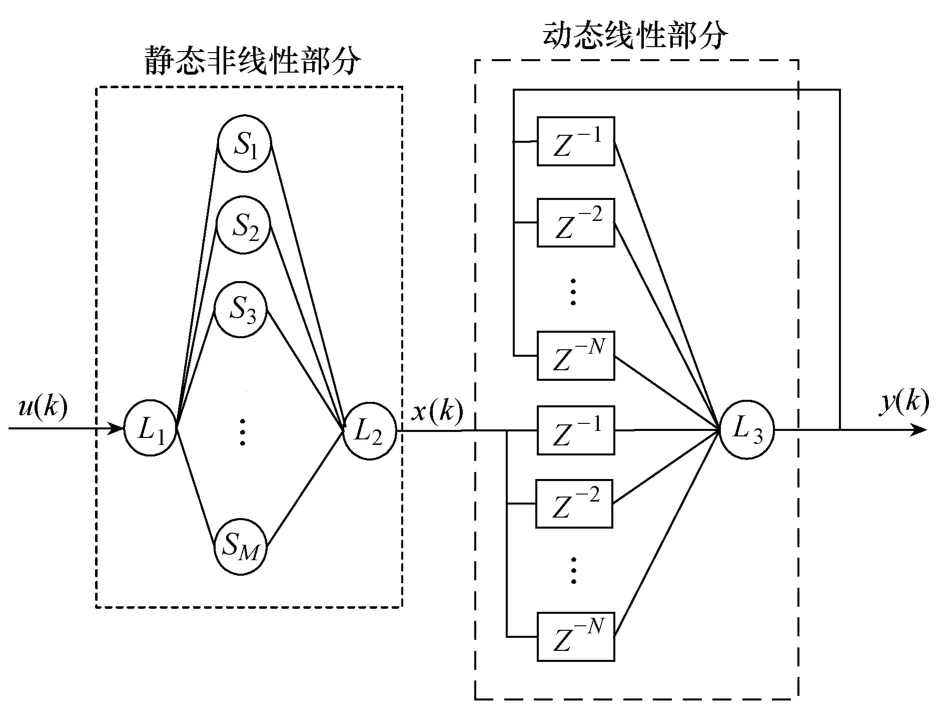
图1 神经网络的拓扑结构
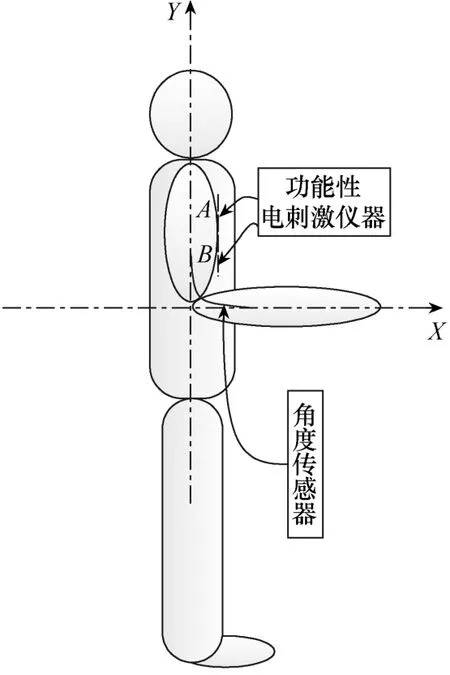
图2 肘关节实验示意图
1.2 实验结果与模型测试
在实验所得 10组数据中随机选择一组的电刺激角度变化数据绘制出曲线,如图3所示。图3(a)为刺激电流脉宽变化曲线,图3(b)为电刺激下肘关节角度曲线。从图3中可知,角度的变化趋势跟随着刺激电流强度的变化而变化,具有非线性和滞后特性。
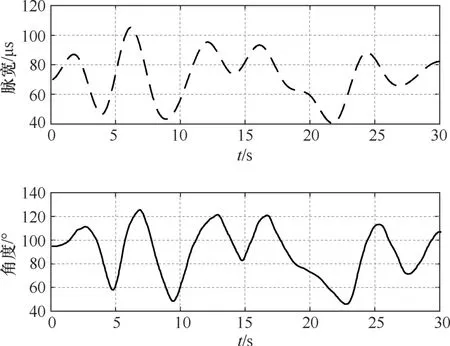
图3 角度变化曲线与刺激电流脉宽
将肘关节建模实验所得的 10组数据中随机选择一组数据用于测试,剩下9组数据用于网络训练。测试样本拟合曲线如图4所示。
计算模型输出与测试数据的最大误差为 9.06°平均相对误差为 4.11%,均方根误差为 4.12°模型输出基本能够跟随测试数据的变化而变化,结果表明所建模型可用。
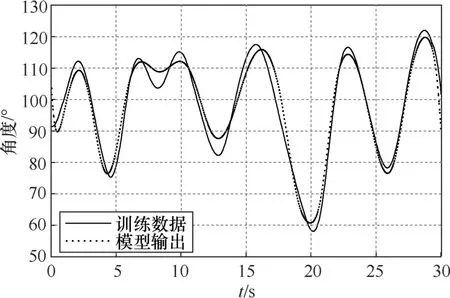
图4 测试样本拟合曲线
2 迭代学习控制系统
2.1 ILC理论与系统设计
迭代学习的控制思想最初是在 1978年由日本的Uchiyama学者提出,之后Arimoto等人与1984年进行了详细的说明[17]。迭代学习控制是通过不断重复的跟踪确定的期望轨迹来获得修正信息,修正控制输入,最终实现实际轨迹与期望轨迹零误差的完全跟踪。肢体功能障碍患者对肘关节的康复训练是根据患者肢体的瘫痪程度制定不同的训练,但是这些训练都有一个共同点,即所有的训练都是指定标准动作重复性运动,每天需要完成多组每组多次的训练。将指定轨迹且重复性质的肘关节训练作为被控对象适合采用迭代学习算法来进行控制。
使用所建立的神经网络肘关节模型,结合 ILC算法建立控制系统。ILC控制系统原理框图如图 5所示。其中θd(t)为期望轨迹,θ(t)为实际轨迹,uk(t)为 k次的控制量,uk+1(t)为 k+1次的控制量。e(t)为期望轨迹与模型输出之间的误差。
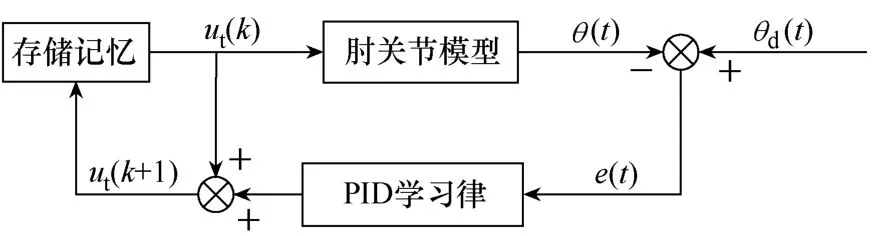
图5 ILC控制系统原理框图
在每一次的迭代过程中,利用k次的控制量uk(t)和跟踪误差ek(t)的PID校正量T(t, ek(t))来构成k+1次的控制输入量uk+1(t),一般化的公式表示为
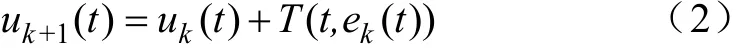
当采用PID型的ILC算法时,T(t, ek(t))的计算为如下表达式:
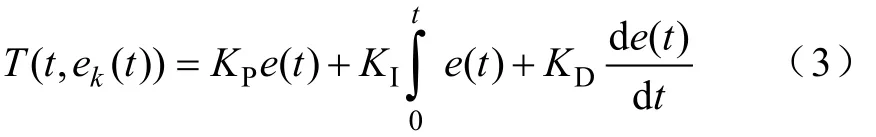
式中,KP、KI和KD为比例、积分和微分系数,其值根据实验进行调节,在本文仿真系统中设置为0.6、0.3和2.0。
迭代学习控制系统的仿真是基于 Matlab/Simulink仿真平台实现的。仿真系统的框图如图 6所示,包括肘关节的神经网络模型和ILC控制器。肘关节模型利用实验数据训练得到神经网络结构体,使用Matlab中的gensim函数将网络结构体转换为Simulink仿真模块。ILC控制器由前一时刻控制量和PID校正量两部分组成,PID校正量采用增量式PID,在仿真中通过S函数实现。其中增量式PID计算表达式分别如式(4)和式(5)所示。
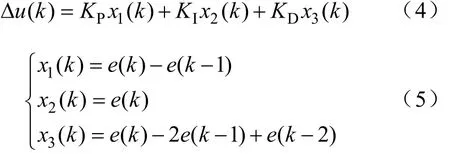
式中,KP、KI和 KD为 PID的比例、积分和微分系数,x1、x2、x3分别为误差一阶差分、误差和误差的二阶差分。
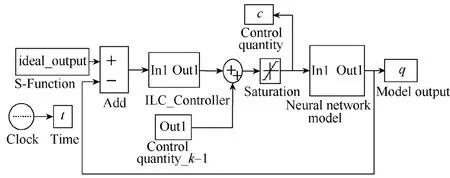
图6 迭代学习控制系统在Simulink中的仿真模型
通过计算期望轨迹与实际轨迹的最大误差、平均相对误差(average relative error, ARE)与均方根误差(root mean square error, RMSE)来评价ILC系统的控制效果。
平均相对误差定义为
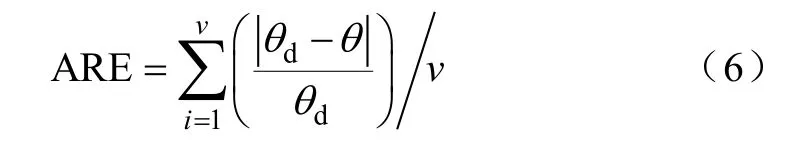
均方根误差定义为
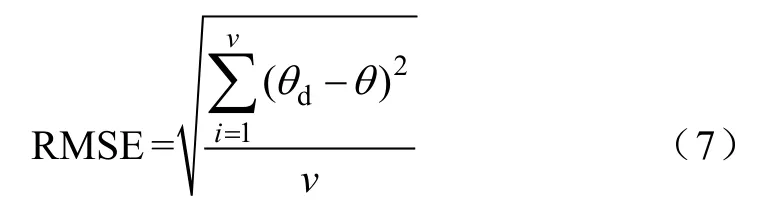
式(6)与式(7)中,v表示样本的个数,θd为期望轨迹,θ 为实际轨迹。
2.2 系统仿真结果与讨论
设定好肘关节运动的期望轨迹对ILC系统进行仿真。期望轨迹的设定是让健康测试者依据图2所示佩戴角度传感器,肘关节均速在矢状面完成收缩和伸展动作,记录运动过程的角度变化作为期望轨迹。期望轨迹例如图7中实线曲线所示。图7中的期望轨迹为健康测试者完成一次收缩与伸展的运动过程。对ILC的FES系统进行10次的迭代,10迭代的期望轨迹与实际轨迹如图7所示。从图7中可知,实际轨迹随着迭代次数的增加越来越贴近期望轨迹。
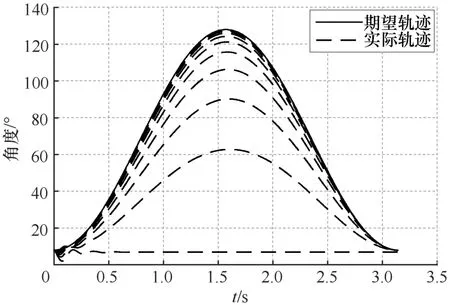
图7 ILC系统10次迭代的期望轨迹与实际轨迹
记录 10次迭代每次迭代期望轨迹与实际轨迹的最大误差与均方根误差,如图8所示。图8(a)为最大误差变化曲线,图8(b)为均方根误差变化曲线。从图8中可知,随着迭代次数的增加,最大误差和均方根误差均下降并且收敛。
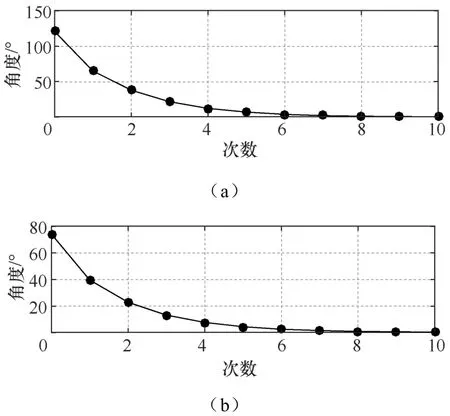
图8 ILC系统10次迭代的最大误差与均方根误差
同时,检验PID控制的FES系统性能。仔细调整PID控制系统中的比例、积分和微分系数,将其分别设置为11.0、10.0和0.6。PID控制下的10个周期的期望轨迹与实际轨迹曲线如图9所示。从图9中可知,实际轨迹并不会随着控制周期的增加而更贴近期望轨迹,其之间的误差始终保持一定值。
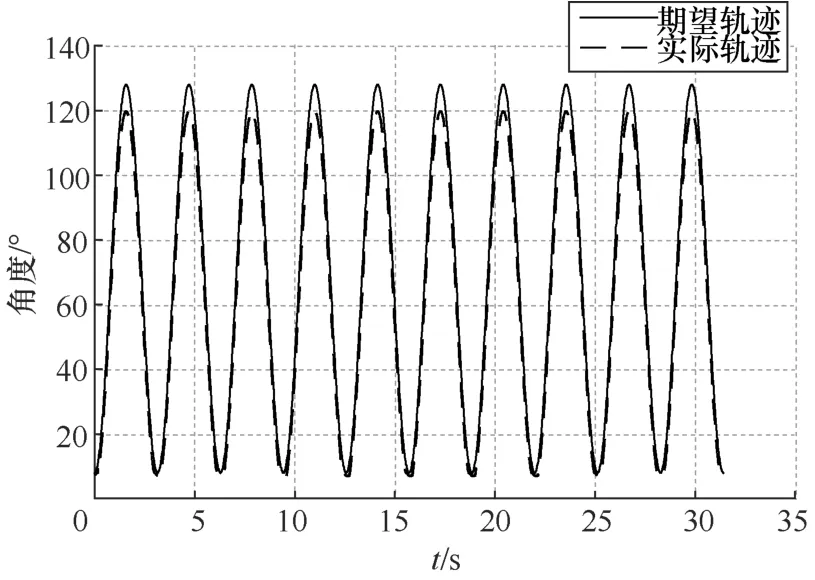
图9 PID系统10个周期的期望轨迹与实际轨迹曲线
比较ILC系统第10次迭代与PID系统第10个周期的实际轨迹与期望轨迹,如图10所示。从图10中可知,ILC输出的轨迹基本与期望轨迹重合,而PID系统的输出轨迹与期望轨迹之间存在较大的误差。计算ILC系统第10次迭代输出轨迹与期望轨迹之间的最大误差、对平均误差和均方根误差分别为0.438°、0.32%和0.245°。同时,计算PID系统第10个周期的输出轨迹与期望轨迹的相应指标分别为 8.263°、14.65%和5.636°。从计算结果可知,ILC系统的指标也明显优于PID系统的指标。
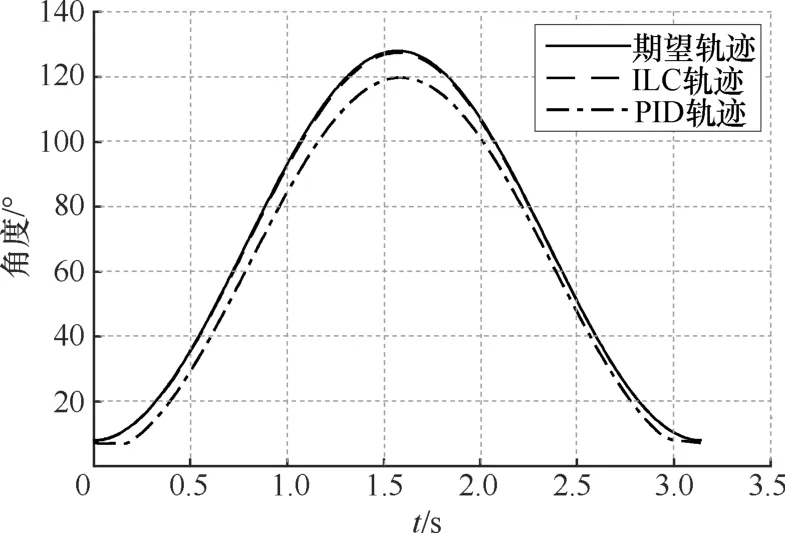
图10 PID和ILC控制系统的输出
从图7到图10可知,ILC的FES系统的性能指标明显优于PID控制的系统。结果表明,相比于PID控制,ILC的方法更适用于电刺激肘关节运动的控制。
2.3 系统抗模型扰动分析
肘关节在电刺激下的运动更容易造成肌肉疲劳,这意味着关节模型参数在训练过程中会发生改变,将影响肘关节的跟踪控制。实验中通过改变神经网络模型参数模拟肌肉疲劳等内部扰动,分析比较PID与ILC算法控制FES系统的结果。随机选择神经网络模型中10%的权值参数进行变化,变化幅值分别为5%、10%和15%。测试比较两种控制系统中期望轨迹与实际轨迹的最大误差、平均相对误差和均方根误差,结果见表 1。分析表 1数据可知,PID控制的系统与ILC的系统中评价指标(即最大误差、平均相对误差和均方根误差)都随着模型改变参数幅值的增大而增大,但是ILC的系统与PID控制的系统相比其指标波动幅值较小,且指标明显优于PID控制的系统。
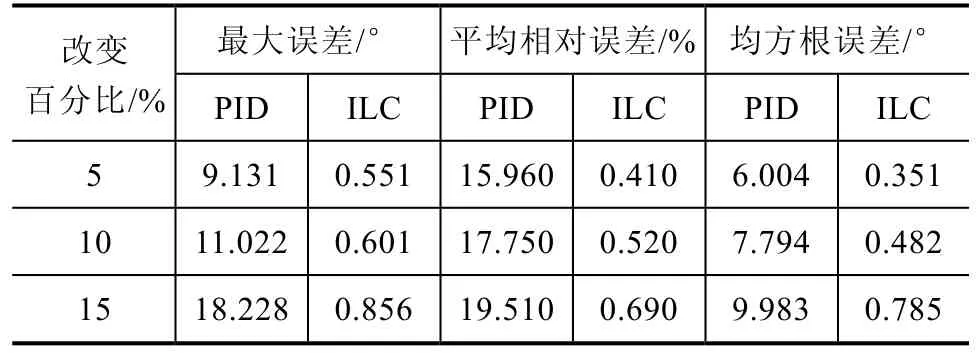
表1 不同模型参数下两种控制系统的性能指标
图11为模型参数变化10%时ILC系统第10次迭代与PID系统第10个周期的实际输出轨迹,在模型参数 10%波动的干扰下,与无模型干扰的图 10相比,ILC系统仍旧可以保持较小的误差,而 PID系统的误差变大。可见,相比于PID控制,模型参数的改变对ILC系统的影响更小,ILC控制的抗干扰性更强。PID控制的系统由于其控制参数(即比例、积分和微分)无法调整,当产生系统内部干扰时,跟踪期望轨迹的效果变差。而ILC算法具有一定的学习能力,能够根据实际输出实时调整控制输入,使得ILC的FES系统具有更强的抗干扰能力。
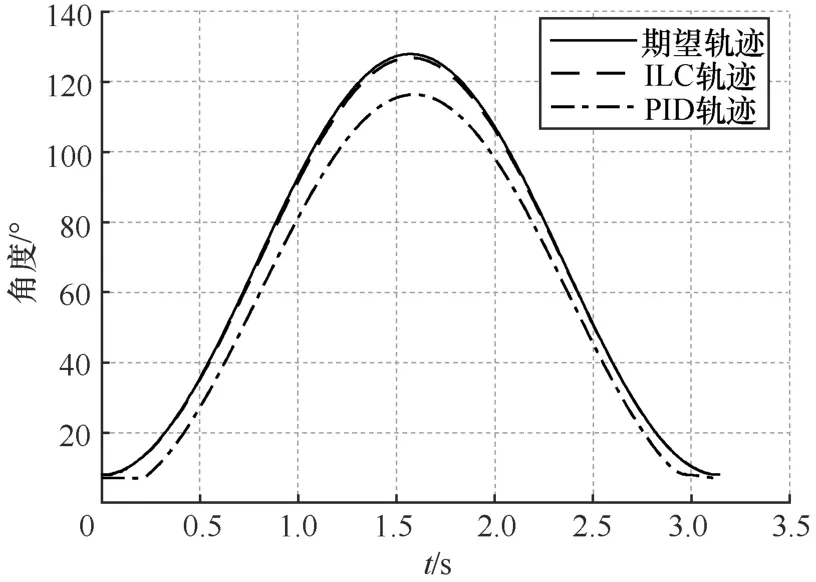
图11 模型参数变化10%时PID和ILC控制系统的输出
3 结论
本文根据肘关节在电刺激下矢状面的运动特性,完成肘关节运动控制的FES系统。建立电刺激量与肘关节运动角度的神经网络模型,结合所建模型设计出ILC算法控制的FES系统。
通过Matlab仿真分析得出ILC方法控制的FES系统,最终迭代次的期望轨迹与实际轨迹之间的最大误差为0.438°,平均误差为0.32%,均方根误差为0.245°。通过模型扰动分析PID系统与ILC系统,得出ILC方法控制下的FES系统具有更强的抗干扰能力,性能指标优于PID方法控制下的FES系统。
本研究通过建立模型来进行仿真,而实际肘关节的电刺激运动特性与所建模型还是有所不同的。未来研究需要以实际人体肘关节为对象,使用 PID与 ILC方法控制的 FES系统进行期望轨迹跟踪实验,完善使所设计的FES系统,使其能够切实帮助肢体功能障碍病人进行康复训练。
[1] 王陇德. 中国脑卒中防治报告[M]. 北京: 人民卫生出版社, 2016.
[2] Yong Huo, Foody J A, Ji L, et al. A systematic literature review of risk factors for stroke in China[J].Cardiology in Review, 2013, 21(2): 77-93.
[3] Furlan J C, Sakakibara B M, Miller W C, et al. Global incidence and prevalence of traumatic spinal cord injury[J]. The Canadian Journal of Neurological Sciences. Le Journal Canadien des Sciences Neurologiques, 2013, 40(4): 456-464.
[4] Liberson W T, Holmquest H J, Scot D, et al.Functional electrotherapy:stimulation of the peroneal nerve synchronized with the swing phase of the gait of hemiplegic patients[J]. Archives of Physical Medicine& Rehabilitation, 1961, 42(8): 101-105.
[5] Boyaci A, Topuz O, Alkan H, et al. Comparison of the effectiveness of active and passive neuromuscular electrical stimulation of hemiplegic upper extremities:a randomized, controlled trial[J]. International Journal of Rehabilitation Research, 2013, 36(4): 315-322.
[6] Bustamante C, Brevis F, Canales S A, et al. Effect of functional electrical stimulation on the proprioception,motor function of the paretic upper limb, and patient quality of Life: A case report[J]. Journal of Hand Therapy, 2016, 29(4): 507-514.
[7] Popović D B. Advances in functional electrical stimulation (FES)[J]. Journal of Electromyography and Kinesiology: Official Journal of the International Society of Electrophysiological Kinesiology, 2014,24(6): 795-802.
[8] Snoek G J, Ijzerman M J, In `t Groen F A, et al. Use of the NESS handmaster to restore handfunction in tetraplegia: clinical experiences in ten patients[J].Spinal Cord, 2000, 38(4): 244-249.
[9] Shimada Y, Ando S, Matsunaga T, et al. Clinical application of acceleration sensor to detect the swing phase of stroke gait in functional electrical stimulation[J]. Tohoku Journal of Experimental Medicine,2005, 207(3): 197-202.
[10] Qiu S, He F, Tang J, et al. Intelligent algorithm tuning PID method of function electrical stimulation using knee joint angle[C]//36th Annual International Conference of the IEEE, 2014: 2561-2564.
[11] Lew B, Alavi N, Randhawa B K, et al. An exploratory investigation on the use of closed-loop electrical stimulation to assist individuals with stroke to perform fine movements with their hemiparetic arm[J].Frontiers in Bioengineering & Biotechnology, 2016, 4.
[12] 赵希梅, 马志军, 朱国昕. 基于迭代学习与FIR滤波器的 PMLSM 高精密控制[J]. 电工技术学报, 2017,32(9): 10-15.
[13] Freeman C T. Upper limb electrical stimulation using Input-Output linearization and iterative learning control[J]. IEEE Transactions on Control Systems Technology, 2015, 23(4): 1546-1554.
[14] Janczak A. Neural network approach for identification of Hammerstein systems[J]. International Journal of Control, 2003, 76(17): 1749-1766.
[15] 陈亚, 李萍. 基于神经网络的短期电力负荷预测仿真研究[J]. 电气技术, 2017, 18(1): 26-29.
[16] 王磊, 曹现峰, 骆玮. 基于改进 PSO 优化模糊神经网络的配电网故障选线研究[J]. 电气技术, 2016,17(3): 30-35.
[17] Arimoto S, Kawamura S, Miyazaki F. Bettering operation of robots by learning[J]. Journal of Robotic Systems, 1984, 1(2): 123-140.
