配电网高阻接地故障时频特征SVM分类识别方法

张君琦 杨 帆 郭谋发

（1. 福州大学电气工程与自动化学院，福州 350116；2. 国网南平供电公司，福建 南平 353000）

配电网系统由于深入居民区，网络复杂，线路距离地面较近，运行时容易接触周围的树枝、建筑物等[1]。配电网线路在接触到具有高阻抗的一些表面，如碎石、沥青、树木、沙砾等物体时，会发生高阻接地故障。同时，如大风、雷击等恶劣的天气原因也会造成高阻接地故障的产生。

高阻接地故障发生时，由于过渡电阻很大，引起的电压、电流突变量并不明显，因此常规保护不能可靠发出动作或报警[1]。高阻接地故障一般会长时间存在，一旦数值不大的故障电流长期存在而不能被发现，将产生严重的后果：故障点电弧燃烧和高温引发火灾，造成电气设备永久性损坏，且高阻接地故障多落于沙地、水泥地等，可能导致人身触电等安全事故，因此需要对其进行快速检测及识别分类，并采取相应措施。

高阻接地故障检测技术过程可以分为 3个部分，包括数据获取、信号处理与特征提取以及合适分类器的选取。

对HIF这样的随机性，非线性、非平稳性、不对称性的信号，用于分析HIF信号的方式可分为4类，即时域、频域、时间尺度域和时频域。文献[2]采用傅里叶变化对电流电压进行谐波分解，提取其3次、5次谐波。时域和频域的分解方法都会导致信号的部分信息丢失，时频信号分解方法弥补了时域法与频域法在信号分解中的弊端。文献[3]采用了 S变换的方法进行信号时频分量的提取，而目前使用较为广泛的是小波分解的方法。文献[4]对馈线的三相电流做离散小波变换后，提取各层的平均值及均方根值为特征量，采用贝叶斯分类器进行分类。文献[5-8]在信号的处理上采用的也是小波分解。虽然小波分解对分析突变信号和奇异信号非常有效，但母小波的选择会影响最终变换的效果。

近几年来，基于机器学习的多种分类器应用于高阻接地故障的识别分类中。文献[9]将决策树算法引入了故障识别中。文献[10]利用支持向量机进行高阻接地故障的识别。

LCD时频分解方法是一种自适应分解的信号分解方法，分解效果好，适应性高。通过LCD时频分解以及带通滤波算法，在配电网发生故障时，构造主变低压侧电流的时频矩阵，求取各频带的标准差为识别特征向量；利用支持向量机（SVM）进行高阻接地故障的分类识别。

1 高阻接地故障识别方法

1.1 配电网高阻接地故障的典型特征

自1977年以来，国内外大量实验和研究分析普遍可以得到高阻接地故障有以下几项典型特征[11]。

1）故障电流变化微弱

高阻接地故障常常发生于水泥、沙地、草皮等表面上，致使接地电阻较大，所产生的故障电流很小，故障点的电流可能只有系统正常运行时负荷电流的10%以下。

2）故障波形随机性强

高阻接地故障发生时常伴随着电弧的熄灭和重燃，并且受接地介质的随机运动的影响，故障回路会间歇性的接通，故障电流会在某一时刻突然增大或减小，具有很强的随机性，无法通过简单的阈值设定来判断故障的发生。

3）故障波形非线性畸变

故障接地点所接触的短路介质多数等效为非线性的电阻，故障电流越小，其包含的谐波幅值会越高。

1.2 高阻接地故障识别方法

本文提出一种基于 LCD带通滤波以及支持向量机（SVM）分类器的配电网高阻接地故障识别方法。在配电网发生高阻接地故障后，利用LCD带通滤波算法构造主变低压侧三相电流波形的时频矩阵，对时频矩阵求取各子频带的标准差作为特征向量；同时，利用支持向量机（SVM）构造分类器，将特征向量输入SVM分类器，实现高阻接地故障与其他相似正常工况扰动（如电容器投切、负荷投切、励磁涌流的情况）的辨识。

图1 配电网高阻接地故障识别方法流程图

1）时频矩阵求取方法与特征量提取

局部特征尺度分解（LCD）是一种针对非平稳信号的分析方法，具有一定的自适应性，其与经验模态分解（EMD）均是对原始信号进行自适应分解，但其在分解速度和迭代次数等方面都优于EMD[12]。

局部特征尺度分解（LCD）方法是假设一个复杂信号是由不同的内禀尺度分量（ISC）分量组成，即可以将一个波形信号分解为多个ISC分量，任两个ISC分量之间是完全独立的。根据所定义的ISC分量，将任意信号进行局部特征尺度分解，分解成几个ISC分量和一个残余项之和[13-14]。

其具体分解步骤如下。

（1）得出原始信号的所有极值点（τk,Xk），k = 1,2,… ,M ，M为极值点个数。由任意两个相邻的极大（或小）值点（τk,Xk）和（τk+2,Xk+2）确定的一条曲线在τk+1时的纵坐标为

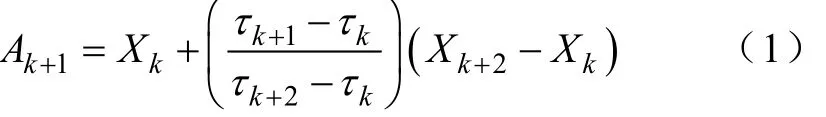
（2）根据式（1）计算出 Ak+（1k =2,3,… ,M −1），利用（τk+1,Xk+1）与（τk+1,Ak+1）进行插值计算，得到一般 a = 0.5。

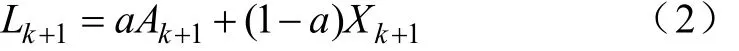
（3）对求取出的所有 L （kk =2,3,… ,M −1）做三次样条拟合得到均值曲线 B L1( t)。

（4）将均值曲线从原信号中分离出来，即

如果 h1( t)满足ISC的定义，则ISC1=h1( t)，执行步骤（5）；否则，以 h1( t)为原始信号重复步骤（1）至步骤（3），直到满足条件为止。

（5）得到剩余信号 r1( t) = x( t) − I SC1，将其作为原始信号重复步骤（1）至（3），得到ISC2。之后，重复以上步骤，直至剩余信号单调或小于阈值时停止，则原始信号可表示为

图 2为高阻接地故障时三相电流波形，其经LCD自适应分解后，得到了一个ISC分量以及一个残余项，得到的ISC分量如图3所示。

图2高阻接地故障主变低压侧三相电流波形

图4 所示的是电容器投切、负荷投切、励磁涌流等正常工况扰动发生时所得到的波形，将这些波形使用相同的步骤进行数据处理以及特征量提取。

为了更直观地表现各个故障波形在时域和频域上的特征，通过LCD带通滤波构造各个故障波形的时频矩阵[15]。利用假设各个波形采样点数均为n，故障波形经LCD带通滤波后分解为m个子频带，各个子频带波形的数据点为ija（i=1,2,…,m；j=1,2,…,n），则可得到时频矩阵为

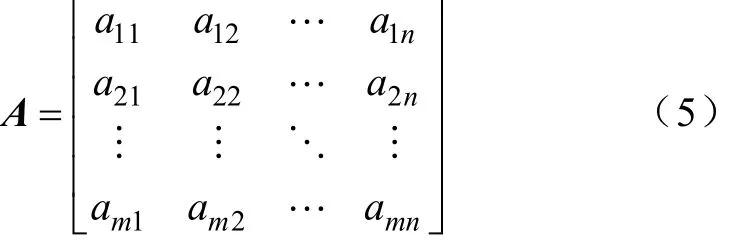
图3 高阻接地故障ISC分量

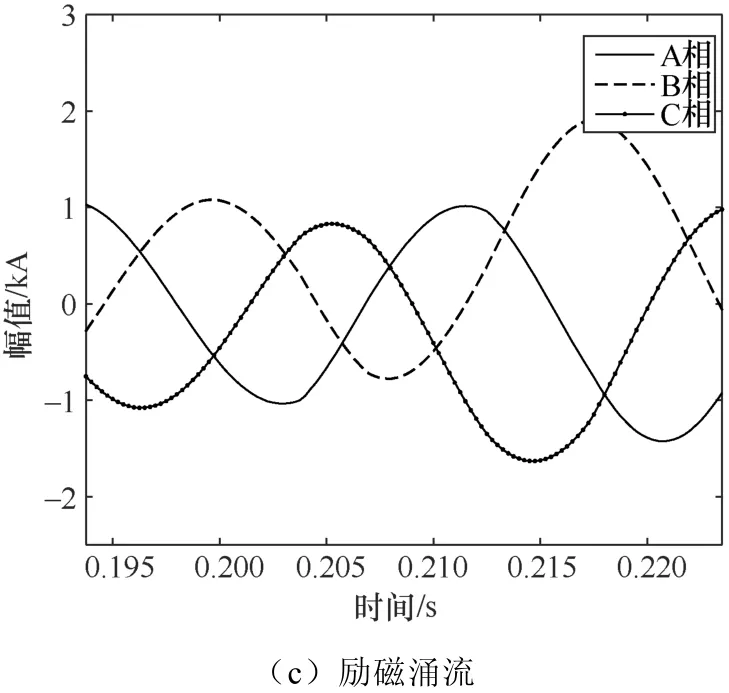
图43 种暂态扰动的主变出线三相电流波形

其中，行表示故障波形经LCD带通滤波后各个子频带的重构波形数据，列表示故障波形的采样时刻。时频矩阵A能够完整地表现了故障波形在各个子频带上的时频信息。

本设计中采样频率为 10kHz，选取的是故障前半周波与故障后一周波的三相电流波形，则采样点数为 120n= 。最大频率为3kHz，选取子频带数 5m=对瞬时频率进行等间隔划分，则第1个子频带范围为0～600Hz，第2个子频带范围为600～1200Hz，依此类推直至第5个频带。

针对得到的时频矩阵求取各频带的标准差作为特征向量，即计算矩阵每一行的标准差，可以得到5个标准差值，因此三相电流波形可以得到15个标准差值作为输入的特征向量。

2）SVM在配电网高阻接地故障识别中的应用

支持向量机（SVM）是一种基于统计学习理论的机器学习算法，是根据结构风险最小化原则所提出。SVM对小样本、非线性、高维度的样本的分类问题上效果优于其他智能技术，已被广泛应用于电力系统故障诊断和图像辨识等领域。为了实现高阻接地故障的识别分类问题，引入了非线性可分支持向量机[16-17]。

构建SVM分类器的主要步骤如下：

1）训练样本特征向量的提取。按照本文的方法提取 N个样本的特征向量，则数据集合为D={(Xl, fl) |l = 1,2,… ,N}， fl∈ { 1,0}代表类别标识，1为高阻接地故障，0为其他运行工况过程。

为使训练样本具备代表性，充分计及暂态过程发生的位置、投入初相角、各参数值大小以及相别等诸多因素对识别结果的影响，在图4的仿真平台上进行高阻接地故障仿真，同时，在此模型上进行其他常见扰动暂态信号，如电容投切、负荷投切以及励磁涌流等情况的仿真，获取不同的暂态信号用于分类，得到的总训练样本数为1008组，样本分布情况见表1。

表1 训练样本分布情况（a）高阻接地故障

2）构建SVM分类器。根据SVM算法，针对上述的训练样本数据集，存在超平面 H ：ωx+b=0，其中ω为最优分类面的法向量，b为分类阈值。

3）参数选取。本文构建的是以径向基（RBF）函数为核函数的SVM，高斯核函数表达式为

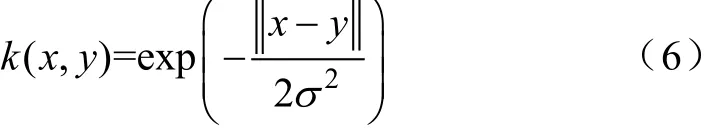
该类SVM的性能主要受2个参数影响：惩罚因子C和核函数核宽度σ，调整惩罚因子C在保证最小误分率的同时可以产生最大的区分间隔，核函数核宽度σ越大，表示样本在高维空间的分布越复杂。参数C与σ的数值形成一个二维向量空间，采用交叉验证的方法进行优化。选取在各次测试中正确率最高的一组参数向量作为最优参数。经训练及参数优化后得到的SVM分类器交叉验证率为96.93%。

2 仿真与建模

2.1 10kV配电网模型

利用 PSCAD/EMTDC仿真软件搭建了一个10kV配电网谐振接地模型，如图5所示。在该配电网模型上进行各种情况的仿真实验，获取主变低压侧三相电流的波形数据。在配电网模型中，T1为110/10kV变压器，其具体参数见表2。10kV侧为中性点经消弧线圈接地系统，系统阻抗0.2Ω。L1是纯架空线路、L2是纯电缆线路、L3—L6是缆线混合线路。F1—F14为故障点。电缆线路正序参数为：R1=0.27Ω/km，C1=0.339μF/km，L1=0.255mH/km；电缆线路零序参数为：R0=2.7Ω/km，C0=0.28μF/km，L0=1.019mH/km。架空线路正序参数为：R1=0.125Ω/km，C1=0.0096μF/km，L1=1.3mH/km；架空线路零序参数为：R0=0.275Ω/km，C0=0.0054μF/km，L0=4.6mH/km。设置各线路的不同接地参数，以模拟配电系统运行时不平衡的状态。

图510 kV配电网模型

表2110 /10kV变压器参数

2.2 高阻接地故障模型

由于高阻接地故障多数伴随着电弧发生，因此无法采用简单的单相接地故障模型来模拟故障。

高阻接地故障模型采用的是基于伊曼纽尔电弧的模型，模型如图6所示，该模型由2个直流源，2个二极管以及2个可变电阻组成正负半周电流的通路[18]。2个直流源Vp，Vn模拟来自电弧的电压，当Vph＞Vp时，电流流向大地；当 Vph＜Vn时，电流反向；当Vph在Vp和Vn之间时，电压被Vp或Vn抵消，无电流流过；改变Vp、Vn的大小会增加故障的随机性和消弧时间。Rp、Rn模拟的是电弧电阻，可以通过调节Rp、Rn来控制故障电流的大小。

图6 高阻接地故障模型

本模型中，直流源Vp=3.0kV，Vn=2.0kV，随机变化为±10%；可变电阻Rp，Rn在[0,50]Ω之间，每0.05ms随机独立变化。在训练及测试过程中所使用的接地电阻范围在0.5～8kΩ之间。

2.3 其他暂态模型

配电系统中有许多正常操作与高阻接地故障有极为相似的暂态波形，比如：电容器投切、负荷投切、变压器空载合闸所产生的励磁涌流。因此，在仿真平台上也对上述的3种情况进行仿真模拟。

1）电容投入。电容器的接线方式一般分为三角形和星形两种方式。本研究采用三角形接线方式。

2）负荷投入。配电网的负荷一般是为感性负荷，因此本次设计中的投切的负荷为阻感性的三相不平衡负荷。

3）励磁涌流。变压器空载合闸的励磁涌流模型的关键模块为双交流模拟变压器剩磁。通过改变电源2的相位来模拟不同分闸角时的变压器的剩磁。控制2个虚拟开关的切换（当BRK2断开时BRK1合闸）来模拟不同剩磁时的变压器励磁涌流，并且为了防止 2个开关切换时电压波形发生畸变，在PSCAD仿真中开关BRK2需要设置为在任何电流大小时均可打开[19]。

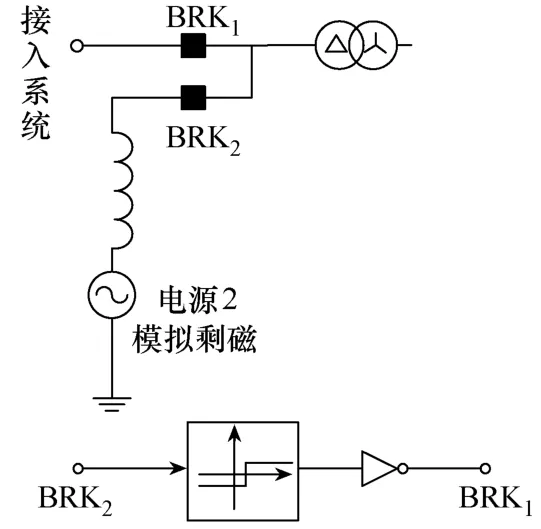
图7 变压器空载合闸励磁涌流模型

2.4 识别结果

综合考虑多个影响因素，选取不同时刻、不同位置以及不同参数值的测试样本（总样本容量为1172组）。根据上述步骤提取出三相电流的时频矩阵各频带的标准差值作为特征向量，总识别正确率可以达到98.24%。

3 识别方法的适应性分析

3.1 适应性实验

为了测试分类算法的可靠性和适应性，对所提出的算法进行适应性分析，考虑的情况包括：中性点接地方式改变、分布式电源接入、网络结构变化。

1）中性点接地方式改变。为了测试识别方法是否能适应不同接地方式的系统，将仿真系统的接地方式改为中性点不接地。

2）分布式电源接入。考虑到配电网中有越来越多的分布式电源接入，故而对分布式电源接入工况的适应性也是一项十分重要的指标。在配电网软件模型中的线路L2末端接入一个分布式电源，电源等效参数采用文献[20]中对小水电站等效得到的参数，等效阻抗为0.02+j1.57Ω。

3）网络结构变化。配电网的结构常常发生变化，因此考虑识别算法在不同网络结构下的适应性，通过增加或减少线路来得到不同的配网网络。考虑减少线路L6改变网络结构变化。

3.2 适应性分析结果

在进行上述几种适应性分析实验时，在F1、F3、F5、F8、F10五处进行各情况的仿真，投入时刻为0°、60°、90°、120°，高阻接地故障中接地电阻为 0.7kΩ、1kΩ、3kΩ、5kΩ，电容投切中电容值为1Mvar，三相负载为 0.5MW/0.25MW/0.25MW，励磁涌流中的剩磁分闸角为30°。

综合以上几种适应性实验的分类测试结果见表3。

表3 适应性分析结果

由表3的实验结果可以看出，即使中性点接地方式以及网络结构的改变，分类算法的正确率达到90%以上。可见，分类算法的适应性较强，在不同情况下均能较好的识别高阻接地故障。

4 结论

结合波形时频矩阵和支持向量机（SVM）提出了一种配电网高阻接地故障的识别方法，对高阻接地故障及一些运行工况进行识别。测试结果表明：

1）利用LCD带通滤波算法构成的时频矩阵能够表征波形在各频带中的时频特征。

2）通过支持向量机验证了利用统计学方法提取特征向量的有效性。

3）提出的识别方法在不同的仿真状态下均有较强的适应性，其识别正确率均可达到90%以上，能有效的用于配电网高阻接地故障的分类识别。

[1] 朱晓娟, 林圣, 张姝, 等. 基于小波能量矩的高阻接地故障检测方法[J]. 电力自动化设备, 2016, 36(12):161-168.

[2] Sharaf A M, Wang G. High impedance fault detection using feature-pattern based relaying[C]//Transmission and Distribution Conference and Exposition, 2003:222-226.

[3] Mishra M, Routray P, Rout P. A universal high impedance fault detection technique for distribution system using S-Transform and pattern recognition[J].Technology and Economics of Smart Grids and Sustainable Energy, 2016, 1(1): 9.

[4] Sedighi A R, Haghifam M R, Malik O P, et al. High impedance fault detection based on wavelet transform and statistical pattern recognition[J]. IEEE Transactions on Power Delivery, 2005, 20(4): 2414-2421.

[5] Michalik M, Lukowicz M, Rebizant W, et al.Verification of the wavelet-based HIF detecting algorithm performance in solidly grounded MV networks[J]. IEEE Transactions on Power Delivery,2007, 22(4): 2057-2064.

[6] Costa F B, Souza B A, Brito N, et al. Real-Time detection of transients induced by High-Impedance faults based on the boundary wavelet transform[J].IEEE Transactions on Industry Applications, 2015,51(6, 2): 5312-5323.

[7] Sedighi A R, Haghifam M R, Malik O P. Soft computing applications in high impedance fault detection in distribution systems[J]. Electric Power Systems Research, 2005, 76(1/3): 136-144.

[8] 陈民铀, 黄永, 瞿进乾. 配电网线路高阻故障识别方法[J]. 重庆大学学报, 2013, 36(9): 83-88.

[9] Samantaray S R. Ensemble decision trees for high impedance fault detection in power distribution network[J]. International Journal of Electrical Power &Energy Systems, 2012, 43(1): 1048-1055.

[10] 郑星炯. 基于支持向量机的配电线路高阻接地故障检测方法[J]. 电子设计工程, 2015, 23(14): 122-125.[11] 耿建昭, 王宾, 董新洲, 等. 中性点有效接地配电网高阻接地故障特征分析及检测[J]. 电力系统自动化,2013, 37(16): 85-91.

[12] 郭谋发, 游林旭, 洪翠, 等. 基于 LCD-Hilbert谱奇异值和多级支持向量机的配电网故障识别方法[J].高电压技术, 2017(4): 1239-1247.

[13] 孙一航, 武建文, 廉世军, 等. 结合经验模态分解能量总量法的断路器振动信号特征向量提取[J]. 电工技术学报, 2014, 29(3): 228-236.

[14] 蔡晋, 林榛, 高伟, 等. 基于 HHT及信号注入的配电网谐振与单相接地故障识别[J]. 电气技术, 2015,16(12): 31-35, 51.

[15] 郭谋发, 刘世丹, 杨耿杰. 采用Hilbert谱带通滤波和暂态波形识别的谐振接地系统故障选线新方法[J].电工电能新技术, 2013, 32(3): 67-74.

[16] 程序, 关永刚, 张文鹏, 等. 基于因子分析和支持向量机算法的高压断路器机械故障诊断方法[J]. 电工技术学报, 2014, 29(7): 209-215.

[17] 魏晓莹, 宋仕江, 郭谋发, 等. 基于振动信号二维特征向量的配变铁心故障诊断[J]. 电气技术, 2016,17(1): 16-21.

[18] Gautam S, Brahma S M. Detection of high impedance fault in power distribution systems using mathematical morphology[J]. IEEE Transactions on Power Systems,2013, 28(2): 1226-1234.

[19] 刘超, 刘健, 张志华, 等. 配电网励磁涌流及其概率分布的分析与探讨[J]. 电力系统自动化, 2017, 41(4):170-175.

[20] 张元胜, 李欣然, 肖园园, 等. 含小水电配网负荷模型实用化方法[J]. 电工电能新技术, 2012, 31(4):83-87.