巧用错题资源 提升学习能力
2018-03-30浙江省宁波市奉化区剡溪中学王祥表
☉浙江省宁波市奉化区剡溪中学 郑 锋 王祥表
所谓错题就是指习题本身在文字语言或者图形语言表述上出现了条件欠缺、互相矛盾或结论不可求证的题目.教师们在教学中经常会遇到一些错题,有的错题题目本身就出现了表达性错误,解答者得不到答案;有些错题没有明显的错误,只有在解答中才会出现相互矛盾的结果.
当我们在教学中发现了错题,通过师生合作、生生合作的方式更正错题,进而对于更正后的错题一题多解,或者变式练习,这种方式有效地激发了学生对数学学习的热情,培养了学习数学的兴趣.数学学习的兴趣一旦激发,课堂效率也随之提高,学生学习能力也得以提升.在美国数学教育家Tam Kieren写的《数学教育研究——三角形》一书中,他提出了把数学教育研究的对象视作三角形的三个顶点,即数学教育是有三个研究方面:课程、教学、学习.而三角形的中心称为“兴趣中心”,指学习者学习数学的兴趣(如图1).
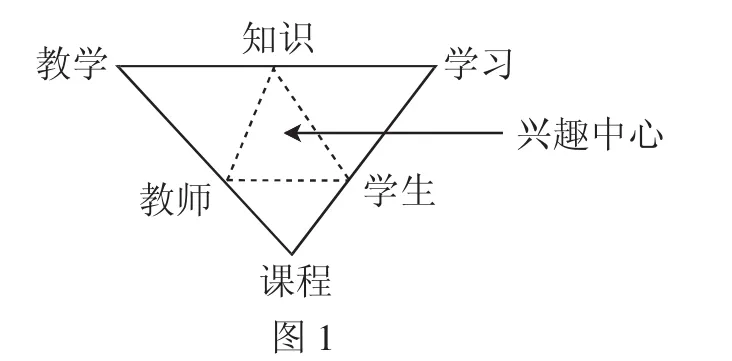
由此可见,错题资源的有效利用,有利于培养学生数学学习的兴趣,也能有效地提高课堂效率,最终转化成学生学习能力的提升.以下是由学生在练习中所发现的一个错题,笔者以此为例谈谈错题资源对学生学习能力提升方面所起到的作用.
一、试题呈现
如图2,在正方形ABCD中,折线AE=3,EF=2,FC=4,∠DAE=∠AEF=∠EFC=60°,则正方形ABCD的边长为______.
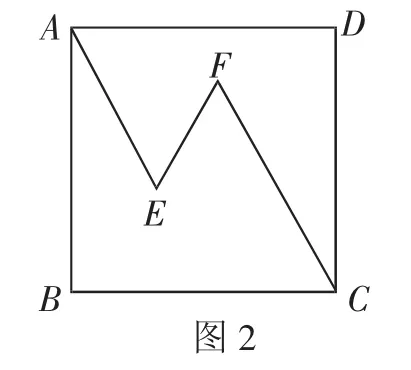
本题条件中出现了正方形及∠DAE=∠AEF=∠EFC=60°,由此学生会朝着正方形的性质、等边三角形、30°特殊直角三角形方向思考,以此添加辅助线.在课堂中,同学们很快解答出了答案,几乎每个同学都有自己的想法,加上参考答案,大致有以下四种解法.

二、解法展示
解法1:如图3,分别延长AE和FE交BC于点G和H.因为在正方形ABCD中,∠AEF=∠EFC=60°,所以AE∥FC.又因为∠DAE=60°,所以可得∠FCH=∠AGB=60°,即△FCH和△EGH为等边三角形.因为AE=3,EF=2,FC=4,所以CH=CF=4,GH=EG=EH=FH-EF=2,AG=AE+EG=5. 因为∠AGB=60°,可得BG=,所以BH=BG-GH=,即BC=解法2:如图3,分别延长AE和FE交BC于点G和H.因为在正方形ABCD中,∠AEF=∠EFC=60°,所以AE∥FC.又因为∠DAE=60°,所以可得∠FCH=∠AGB=60°,即△FCH和△EGH为等边三角形.因为AE=3,EF=2,FC=4,所以CH=CF=4,GH=EG=EH=FH-EF=2,AG=AE+EG=5.因为∠AGB=60°,可得,所以AB
解法3:如图3,分别延长AE和FE交BC于点G和H.因为在正方形ABCD中,∠AEF=∠EFC=60°,所以AE∥FC.又因为∠DAE=60°,所以可得∠FCH=∠AGB=60°,即△FCH和△EGH为等边三角形.因为AE=3,EF=2,FC=4,所以CH=CF=4,GH=EG=EH=FH-EF=2,即CG=2.设正方形的边长为x,在Rt△ABG中,因为∠BAG=30°,所以AB=G,可列得方程x=x-2),解得x=3+
解法4:(参考答案)如图3,分别延长AE和FE交BC于点G和H.因为在正方形ABCD中,∠AEF=∠EFC=60°,所以AE∥FC.又因为∠DAE=60°,所以可得∠FCH=∠AGB=60°,即△FCH和△EGH为等边三角形.因为AE=3,EF=2,FC=4,所以CH=CF=4,GH=EG=EH=FH-EF=2,即CG=2.设正方形的边长为x,在Rt△ABG中,可列得方程x2+(x-2)2=52,解得x=
四种不同的解法得到了不同的结果,解题思路也都正确,同一个题出现了不同的结果.或许当我们在教学中遇到此类问题的时候有些老师可能会告诉学生“这是一个错题”,或许就错过了一个利用错题再学习的机会.巧妙地利用错题,不仅能解决了错题本身的问题,还能激发学生解决错题的兴趣,也进一步提升了学生发现问题、提出问题、探究问题、解决问题的能力,从而促进学生学习能力的提高.
对于上述错题,笔者通过师生合作、生生合作的方式对该题进行了探究.以下是一段师生对话的内容.
生1(鼓足勇气):会不会这题目有问题?
师:为什么?你是怎么看的?
生2:一个题目如果有多个答案,那肯定是分类讨论的结果.但是该题没有这个必要.许多学生表示赞同.
师(竖起大拇指):这位同学非常有勇气,敢于质疑.请大家记住:提出一个问题往往比解决一个问题更为重要,这就是创新啊!既然大家都觉得这个题目有问题,那它错在哪,我们可以如何进行改进呢?
生3:根据解法1和解法2,AB和BC的值不同,我觉得这应该是一个矩形.所以可以把“正方形”改成“矩形”.
师:你很善于观察发现.其实“矩形ABCD”、“折线AE=3,EF=2,FC=4”和“∠DAE=∠AEF=∠EFC=60°”这三个条件是并列的,要不我们将后面六个条件任意删去一个试试.
三、试题改进
变式1:在矩形ABCD中,折线AE=3,EF=2,FC=4,∠DAE=∠AEF=∠EFC=60°,则矩形ABCD的长和宽分别为______.

解:如图4,分别延长AE和FE交BC于点G和H.因为在矩形ABCD中,∠AEF=∠EFC=60°,所以AE∥FC.又因为∠DAE=60°,所以可得∠FCH=∠AGB=60°,即△FCH和△EGH为等边三角形.因为AE=3,EF=2,FC=4,所以CH=CF=4,GH=EG=EH=FH-EF=2,AG=AE+EG=5.因为∠AGB=60°,可得,所以BH=BG-,即BC=因为∠AGB=60°,可得,所以
变式2:在正方形ABCD中,折线EF=2,FC=4,∠DAE=∠AEF=∠EFC=60°,则正方形ABCD的边长为______.

解:如图5,延长AE交BC于点G.因为在正方形ABCD中,∠AEF=∠EFC=60°,所以AE∥FC.又因为∠DAE=60°,所以可得∠FCH=∠AGB=60°,即△FCH和△EGH为等边三角形.因为EF=2,FC=4,所以CH=CF=4,GH=EG=EH=FH-EF=2,即CG=2.设正方形的边长为x,在Rt△ABH中,因为∠BAG=30°,所以AB=,可列得方程x=x-2),解得x=

变式3:在正方形ABCD中,折线AE=3,FC=4,∠DAE=∠AEF=∠EFC=60°,则正方形ABCD的边长为______.
解:如图6,分别延长AE和FE交BC于点G和H.因为在正方形ABCD中,∠AEF=∠EFC=60°,所以AE∥FC.又因为∠DAE=60°,所以可得∠FCH=∠AGB=60°,即△FCH和△EGH为等边三角形.设AB=x,EF=a,在Rt△ABH中,因为∠BAG=30°,可列得方程,
变式4:在正方形ABCD中,折 线 AE=3,EF=2,∠DAE=∠AEF=∠EFC=60°,则正方形ABCD的边长为______.
解:如图7,延长CF交AD于点G,其余过程同变式2.
变式5:在正方形ABCD中,折线AE=3,EF=2,FC=4,∠DAE=∠AEF=60°,则正方形ABCD的边长为______.
解:解答过程同上述的解法4.
变式6:在正方形ABCD中,折线AE=3,EF=2,FC=4,∠DAE=∠EFC=60°,则正方形ABCD的边长为______.
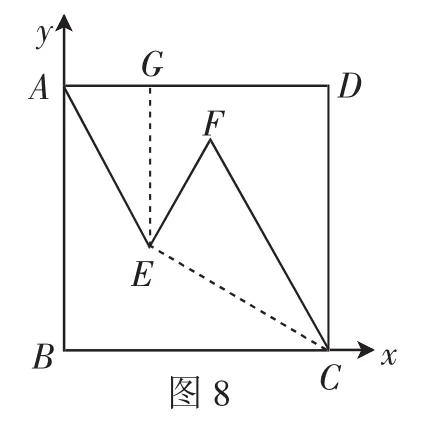
解:如图8,分别以AB和BC所在的直线建立平面直角坐标系,点D的坐标为(a,a),过点E作EG⊥AD,垂足为G,再连接EG.因为AE=3,∠DAE=60°,所以点E的坐标为因为EF=2,FC=4,∠EFC=60°,所以EC=.根据点C和点E的两点距离公式,可列得,解得a=
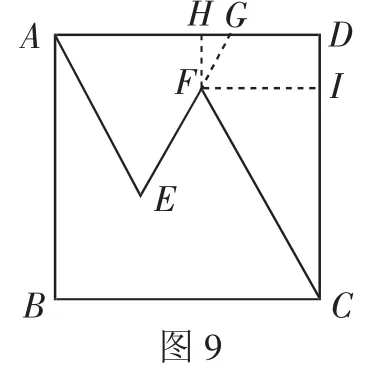
变式7:在正方形ABCD中,折线AE=3,EF=2,FC=4,∠DAE=∠EFC=60°,则正方形ABCD的边长为______.
解:如图9,延长EF交AD于点G,过点F分别作FH⊥AD,FI⊥CD,垂足分别为H和I.因为∠DAE=∠EFC=60°,所以△AEG为等边三角形.因为AE=3,EF=2,可得FG=EG-EF=设正方形的边长为x,在Rt△CFI中,解得
通过师生、生生合作,巧妙地利用了习题中的错题,将错题视为一种再学习的资源,通过错题不仅回顾了正方形、等边三角形、30°特殊直角三角形的性质以及常规的辅助线的做法,也复习了解题中运用的方程思想、转换思想等.巧妙地利用错题资源进行错题更正,变式练习,将学生单纯地掌握知识提升到了运用知识进行命题的新高度,学生的学习能力也达到了另一个境界.
四、几点思考
建构主义观点认为:数学的知识不可能仅仅依靠正面的示范和反复的练习得以巩固,必须有一个自我否定、自我纠错的过程.所以,学生所犯的“错误”是我们宝贵的教学资源.同样,少数的试题“错误”,如不严密、条件少、条件多……在平时的教学中,如能发现及时,并处理得当,将会使课堂增色不少.正如上述的试题,“错误”在于条件过多,七个条件中只要任意删去一个都是一道好题,而且有个别题的思维含量还挺高的.
所以在课堂上出现不同的“错误”时,我们切不可自乱阵脚,应当要惜“宝”,要有自己的“待错”态度:容错——思错——纠错.
1.容错
对待学生的错误我们或许会理性和宽容,但是对待试题中的“问题”,可能就有老师说了:“题目有问题,这是一个错题.”其实,题目出得不严谨固然不对,需要克服,但是既然遇到了这个问题,我们不如“将错就错”,好好利用好这个“错题”.
2.思错
在上述的试题呈现出几种不同的答案时,学生达到了最高的兴奋点.他们都想从别人的解答过程中看出什么破绽,但是又无济于事,心里一直在想:到底“错在哪”.这是学生思维最为活跃的时候,也是最会产生智慧火花的时候.首先,他们肯定先检查一番自己的解答过程,确定无误后,再次回到题目上去,看是否审题出错,当所有的检查都确认没有错误时,就有个别学生大胆地提出疑问:会不会是试题有问题?
3.纠错
通过师生、生生合作共同思错,接下来的纠正错误也就水到渠成、迎刃而解了.试题不是条件多了吗,那我们就一起进行压缩,把出现的新问题再一起解决.所以对待教学中的一些“错误”,有时候不妨“将错就错”,或许能因错而美.
五、结束语
错题资源的巧妙运用能让学生全面参与到问题的认知、探索、发现、设计中去,获得系统性的知识,并提升合作学习、自主学习的能力.通过错题资源的合理运用,使课堂教学方式和模式多样化,既梳理了知识内容,也使学生学习能力得到了有效的提升,同时也激发了学生的学习兴趣.错题不再是实际意义上的错题,而是一种再学习的资源,只要我们在教学中多思考、多利用,学生的学习兴趣激发了,学生的学习能力也提升了.
1.李政涛.教育常识[M].上海:华东师范大学出版社.2016.
2.曹文喜.由课本一道习题所想到的——浅论几何题目的命制[J].中学数学(下),2016(12).
3.刘华为.基于知识溯源 探究解法自然[J].中学数学教学参考:中旬,2016(5).
4.季春兰.浅谈如何激发学生的学习兴趣——以一堂综合实践课的教学为例[J].初中数学教与学.2012(11).J
