探究经典 推陈出新

☉湖北省阳新县白沙中学 罗 峻

☉武汉市汉南区纱帽中学 段利芳

在日常数学教学中，我们常会碰到一些陈题.所谓陈题，是指以前常考的题目或研究过的题目，其中，不乏经典“名题”.对教师而言，见过的陈题太多，往往会从心底摒弃这些题目，于是千方百计地搜集大量的新题，进行了大运动量的练习，结果适得其反，收效甚微.其实，如果能对这些经典陈题作些适度的探究和挖掘，进行一题多解、一题多变等训练，那么可以获得具有探索性的问题及有价值的解法，进而有效地训练学生思维的灵活性和深刻性，提高学生的推理能力、探究能力及创新意识.下面以一道经典陈题为例说明如下，供读者参考.

一、原题再现

如图1，已知△ABC是等边三角形，延长BC到D，延长BA到E，且使AE＝BD，连接CE、DE.求证：CE＝DE.

二、解法探究

这是一道典型的几何证明题，涉及等边三角形性质及等腰三角形的判定，对初学几何知识的初中生来说有一定的难度.给出的图形中，线段CE和DE无法直接证明，既无法证明∠ECD＝∠EDC，也无法证CE、DE所在的三角形全等.因此，应想到作辅助线，而作出适当的辅助线，是初学者的软肋.初看题目，与课本一道习题的图形有很大联系（见“试题起源”中的图形），于是产生了下面的解法.

思路一：利用△ABC是等边三角形的条件，过某个点作平行线，产生新的等边三角形，再证与CE、CD有关的三角形全等.

证法一：过点E作平行线，产生以BE为边的等边三角形.

证明：如图2，过E点作EF∥AC交BD的延长线于F.

由△ABC是等边三角形和平行线的条件易知，△BEF是等边三角形，所以BF＝BE＝EF.

又BC＝AB，则CF＝AE＝BD，则BC＝DF.

又∠B＝∠F＝60°，

所以△EBC≌△EFD（SAS），

所以CE＝DE.

注：作平行线后，把△BED补成等边三角形，产生相等的线段，为三角形全等铺平道路.也可以说△EBC与△EDF关于CD的垂直平分线对称.证明所用的图形、方法与课本习题类似.

证法二：作两条平行线，产生两个等边三角形.

证明：如图3，过点E作EF∥AC交BD的延长线于F，过点D作DG∥BE交EF于点G.

由△ABC是等边三角形，易证△BEF、△GDF也是等边三角形，那么四边形ACFE是等腰梯形，则CF＝AE＝BD，则BC＝DF.又∠EAC＝∠EGD＝120°，AE＝EG，AC＝DG，

所以△ACE≌△GDE（SAS），

所以EC＝ED.

注：作两条平行线后，产生了新的轴对称图形，这样的轴对称图形不止一个：△EBC与△EFD，△BED与△FEC，△EAC与△EGD，△ABC与△GFD，它们都关于CD的中垂线对称，这样又会产生几种证法，证法可类比证法二，这里略去.

证法三：作平行线，得到以AE为边的等边三角形.

证明：如图4，过点E作EF∥BD交CA的延长线于F.

由△ABC是等边三角形，易知△AEF也是等边三角形，

所以EF＝AE＝BD，∠F＝∠B＝60°，CF＝BE，

所以△CEF≌△EDB（SAS），

所以CE＝DE.

注：证法三充分运用AE＝BD这个条件，以AE为边作等边三角形，证以CE、DE为边的三角形全等.

证法四：作平行线，得到以BD为边的等边三角形.

证明：如图5，过点D作DF∥AC交BE于F，则△BDF是等边三角形，

所以FD＝BD＝BF＝AE.

由AE＝BF，得EF＝AB＝AC，

又∠CAE＝∠DFE＝120°，

所以△EFD≌△CAE（SAS），

所以CE＝DE.

注：证法四的实质是构造以BD为边的等边三角形，再证分别以ED、CE为边的三角形全等.

证法五：作两条平行线，在BD下部以BD为边作等边三角形.

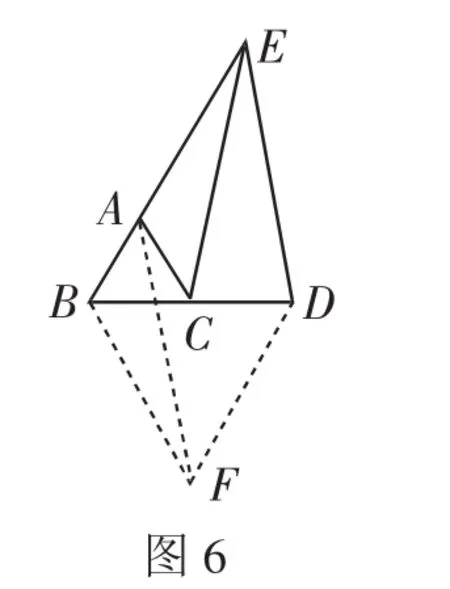
证明：如图6，分别过B、D点作AC、AB平行线交于点F，连接AF.

由△ABC是等边三角形，易证△BDF也是等边三角形，

易证AC＝AB，BF＝BD＝AE，∠EAC＝∠FBA＝120°，

则△EAC≌△FBA，

所以AF＝CE. ①

则AF＝DE. ②

结合①②得CE＝DE.

注：作两条平行线后，会产生两个特殊图形：等边三角形和平行四边形，这样为证全等提供了多个条件.

思路二：受证法五启示，作平行四边形，得出等边三角形，再证有关三角形全等.

证法六：如图6，以AE、DE为邻边作▱AEDF，连接BF.

由BD＝AE，AE＝DF，则BD＝DF，

而DF∥BE，∠B＝60°，则∠BDF＝60°，

所以△BDF是等边三角形，

所以∠ABF＝∠EAC＝120°，AB＝AC，BF＝BD＝AE，

所以△EAC≌△FBA，

所以AF＝CE，由平行四边形知，AF＝DE，

所以CE＝DE.

证法七：如图7，以AB、BD为邻边作平行四边形ABDF，连接EF.

由AE＝BD＝AF，∠EAF＝60°，

易知△EAF是等边三角形，

则∠EAC＝∠EFD＝120°，AE＝EF，AC＝AB＝DF，

所以△ACE≌△FDE（SAS），

所以EC＝ED.

证法八：如图8，以DE、BD为邻边作平行四边形BDEF，连接FA，则∠FEB＝∠EBD＝60°，由平行四边形对边相等知，EF＝BD＝AE，

所以△AEF是等边三角形，

所以∠EAF＝60°＝∠BAC，

所以点F、A、C在同一条直线上.

易证FA＝EA，∠FAB＝∠EAC＝120°，AB＝AC，

所以△FAB≌△EAC，

所以EC＝BF＝DE.

注：思路二中的三种证法，即证法六、七、八，思路别具一格，都是先作平行四边形，再证等边三角形，最后证三角形全等，所用的知识点较前面五种证法更多，方法更灵活，综合性增强了，沟通了各知识间的联系与契合点，是创新思维的再一次运用.

思路三：利用30°的直角三角形的性质和线段的中垂线.

证法九：作三条垂线.

如图9，过点C作CF⊥BD于C点，过点E作EH⊥CF交BD于H，过点F作FG⊥EH于G.

由∠B＝60°知，∠BFC＝30°，

所以BF＝2BC.又BC＝AB，则BA＝AF.

由∠FEG＝30°知，EF＝2FG＝2CH. ①

由BD＝AE，BC＝AF知，CD＝BD-BC＝AE-AF＝EF. ②

结合①②得EF＝CD＝2CH，即H为CD中点，进一步得EH为CD垂直平分线，

所以CE＝DE.

证法十：作一条垂线.如图10，过点E作EF⊥BD于F，易得∠BEF＝30°，所以BF＝①

由△ABC是等边三角形，

所以AB＝BC.

又AE＝BD，BF＝BC＋CF，

所以由①得2BF＝BE＝AB＋AE＝BC＋BD＝BC＋（BC＋CD）＝2BC＋CD. ②

所以EF为线段CD的垂直平分线，

所以CE＝DE.

注：60°的角是一个特殊条件，与直角结合起来后会有定理“30°角所对的直角边是斜边的一半”，证法九和证法十正是遵循这一特征，实现条件之间的转化，证得EH（EF）为线段CD的垂直平分线.解答过程虽然迂回曲折，但另辟蹊径，为初学者提供了一次绝好的思维训练，应该值得肯定.

三、试题起源

仔细观察原题及证法一可以发现，该题由人教版八年级上册第82页第6题改编而来，具体题目如下：如图11，点D，E在△ABC的边BC上，AB＝AC，AD＝AE.求证：BD＝CE.［1］

对照课本题目与本文原题可以发现：将课本题目图形中的AC、CE去掉，赋予∠ABC＝60°，并以BD为边作等边三角形，即为本文原题.本文原题的证法一正是受课本题目的启示，作平行线补全图形，证三角形全等，这也是绝大多数学生最先想到的证法.

课本例题和习题具有较强的示范性和权威性，将它们衍变会得出一个个新的甚至颇富思维含量的考题，可见课本是推陈出新的源泉.对演变的题目进行多角度的分析与解答，不仅能使学生巩固所学的新知识，学会运用新知识解决实际问题，而且还有助于学生掌握和运用数学思想方法，提高学生分析问题、解决问题的能力.

四、变式探究

张奠宙先生说：“变式练习是中国数学教育的一个创造.”作为教师应抓住习题之间的联系，引导学生对典型习题进行演变、拓展和应用.习题的每个变式，看似重复但都具有创新成分.通过变式练习，教师为学生的思维发展提供了一个个不断向上的阶梯，有利于学生夯实基础，建构完整合理的知识体系，发展数学思维和能力.

变式1：原题背景不变，将△ABC放大，并赋予数值，求线段长.

题目1：如图12，等边三角形ABC的边长是4，D在BC上，E在BA的延长线上，且CE＝DE，若AE＝2，求BD的长.

解析：如图13，延长BC到F，使CF＝AE＝2，则BE＝BF.

因为△ABC是等边三角形，所以△BEF也是等边三角形，易证△BDE≌△FCE，所以BD＝CF＝2.

说明：本题将原题中的△ABC放大，并将条件与结论互换，解决问题的思路和方法并没有改变.

变式2：探索原命题的逆命题.

题目2：如图14，已知△ABC是等边三角形，E在BA的延长线上，D在BC的延长线上，且ED＝EC.求证：AC＋DC＝AE.

说明：本题实质是原题的逆命题，只是求证的结论写成两条线段的和的形式，证明的思路方法并没改变，解答过程略.

变式3：探究原命题的大前提.

题目3：如图15，已知△ABC中，∠B＝60°，延长BC到D，延长BA到E，使AE＝BD，连接CE、DE，若CE＝DE，求证：△ABC是等边三角形.

证明：如图16，延长BD到F，使DF＝BC，连接EF.

又CE＝DE，∠BCE＝∠EDF，则△BCE≌△FDE，

因此BE＝EF.又∠B＝60°，所以△BEF是等边三角形，

则BE＝BF.

又AE＝BD＝CF，即AE＝CF，

所以AB＝BC，而∠B＝60°，所以△ABC是等边三角形.

说明：本题设置的命题背景不变，将结论CE＝DE变为条件，进一步探究原命题的前提条件，△ABC是否为等边三角形.

变式4：改变部分条件，探求角的度数.

题目4：如图17，△ECD中，EC＝ED，A是三角形外一点，且∠ECA＝60°，AC＋AD＝EC.求证：∠EDA＝60°.

解析：如图18，延长CA到F，使CF＝CE，连接EF、AE.

由∠ACE＝60°，CF＝CE知，△CEF是等边三角形，

则EF＝CE＝DE. ①

由AC＋AD＝EC和AC＋FA＝FC＝EC知，AD＝FA. ②

结合①②和公共边AE知，△AEF≌△AED（SSS），

所以∠EDA＝∠F＝60°.

注：本题实际将本文原例题中的图形，BA和BC隐去，并将已知与结论互换，来设置题目.解题的方法与原命题类似，都是利用60°角的条件来构造等边三角形，再证三角形全等.

变式5：改变C点位置，增设条件，探究线段和差关系.

题目5：如图19，已知△ABC中，AB＝AC，D是△ABC外一点，且∠ABD＝∠ACD＝60°，求证：BD＋CD＝AB.

证明：如图20，延长BD至E，使DE＝CD，连接AE.

因为∠ABD＝∠ACD＝60°，所以A、B、C、D四点共圆.

由四边形ABCD对角互补、等腰及圆周角定理得

∠ADC＝180°-∠ABC＝180°-∠ACB＝180°-∠ADB＝∠ADE，即∠ADC＝∠ADE.

又边AD公共，CD＝DE，

所以△ADC≌△ADE，

所以∠E＝∠ACD＝60°，

所以△ABE是等边三角形，

所以AB＝BE＝BD＋DE＝BD＋CD.

说明：本题实际是“题目4”的逆命题，证明的难度增加不少.本题利用60°角的条件，把△ABD想象成等边三角形的一部分，运用补形法解题.解题的关键是运用四点共圆找出隐性圆，并运用圆周角进行角的转化，后面容易得出两个三角形全等和另外一个等边三角形，其解法极富思维含量.

变式6：改变C点位置，增设条件，探究线段的大小.

题目6： 如图21，∠ABD＝∠ACD＝60°，∠ADB＝90°-DC，比较：线段AB与AC大小，并证明你的结论.

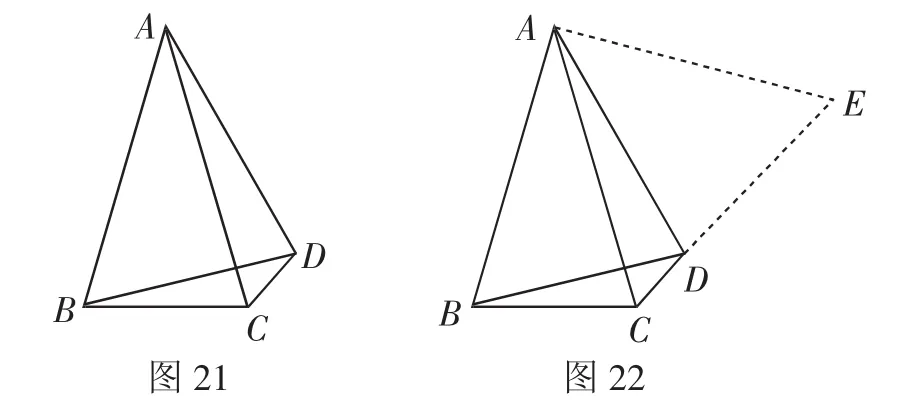
解析：如图22，以AC为边在形外作正△ACE，则D在CE上，AC＝AE，∠E＝60°. 又因为∠ADB＝90°BDC，所以∠ADE＝180°-∠ADB-∠CDB＝180°-∠BDC）-∠CDB＝90°∠BDC＝∠ADB，即∠ADE＝∠ADB，∠ABD＝∠E＝60°，AD＝AD，

所以△ADB≌△ADE，于是AB＝AE，从而AB＝AC.

说明：解题的关键是还是利用60°角构造等边三角形，并如何将条件“∠ADB＝90°-1∠BDC”有效转化，为

2此将∠ADB放在平角中考虑问题，得出∠ADB＝∠ADE，为后面的全等作铺垫.

变式7：补全图形，去掉AC，探究图形特殊形状.

题目7：如图23，设C、D为线段BF上的两定点，且BC＝DF，E为BF外一动点，当E点运动使∠BEC＝∠DEF时，△BEF为等腰三角形吗？并证明你的结论.

解析：如图24，作△BEF的外接圆，并延长EC、ED交△BEF的外接圆于M、N，连接BM和FN.

由∠BEC＝∠DEF，则弧B（M＝F（N，则BM＝FN， ①

那么B（N＝F（M，其所对的圆周角∠BFN＝∠FBM. ②

结合①②和BC＝DF知，△BCM≌△FDN（SAS），

所以∠M＝∠N，所以B（E＝E（F，则BE＝EF，

所以△BEF是等腰三角形.

说明：本题实际是本文提到的课本练习题的逆命题.解决本题通过作出三角形外接圆，并运用圆的最重要的两个性质——圆心角定理和圆周角定理，来实现圆弧与线段及角度之间的转化，思维跨度大，解法独特，虽然是一道年份较久远的数学竞赛题，现在做起来，同样很有思维价值.

五、一点感想

现在许多教师把教学的主要精力放在寻找网络教学资料、制作课件、上课、批改作业和讲评题目等环节，而很少有人愿意花较多时间去进行解题研究.尽管有的教师为了教学需要解一些综合题，但也是为了求得答案，保证课堂教学的顺畅.如果这样长此以往，课堂教学会很低效，不利于发展学生的思维能力.因此，在平时教学中，应在海量的习题中筛选的基础上，结合教材、辅导和命题经验精选、批选典型习题，其实陈题、旧题都无所谓，只要方法够典型就行.

美国著名数学家、数学教育家波利亚曾说过：“解题，就好像游泳一样，是一种实际技能.当你学习游泳时，你模仿其他人的手足动作使头部保持在水面上，并最后通过实践（实地练习游泳）来学会游泳，当试图解题时，你也必须观察并模仿其他人在解题时的行为，并且最后通过实践来学会解题”.因此在教学中教师应该精选一些与所授内容有关联的典型问题，进行多角度解答.因为同一道数学题，可能有不同的解法，解题方法的不同，决定了“长度”的不同，难易程度的不同，适用的普遍性不同，而数学的一个重要崇尚法则就是解题的简单性.数学教师的教学任务之一，不但要引导学生怎样去探究同一问题的不同解法，让学生体会、揣摩、模仿解题，学会“游泳”；还要对这些解法作对比，哪些方法最简单、最实用.这样让学生体验到解决问题方法的多样性，探究问题的深刻性和广阔性，择优比较中的独创性、灵动性.

波利亚指出，“拿一个有意义而不复杂的题目去帮助学生发掘问题的各个方面，使得通过这道题就好像通过一道门户，把学生引入一个完整的领域”，引导学生一题多变，将经典题目适当引申、拓展，不仅能够激发学生的学习兴趣，巩固新知，而且能在更广阔的数学空间中探究几何图形的性质，感受图形、题目之间的内在相互联系，优化思维过程，完善认知结构.通过变式训练，对教材中的例题、习题进行纵向或横向的拓展，能加深学生对诸多知识和方法的理解，给学生营造一个“再发现”“再创造”的探究氛围，变式教学给人一种新鲜、生动的感觉，能唤起学生的好奇心和求知欲，能产生主动参与学习的动力，保持对学习活动的兴趣和热情.通过变式，学生学会从事物之间的联系的矛盾上来理解事物的本质，在一定程度上可以减少思维僵化及思维惰性，从而更深刻地理解课堂教学的内容.

总之，在教学中，教师应该精挑细选一些经典考题，多角度分析探究解法，解题时应总结思路，反思回顾，并提供该类题型的知识储备、链接式讲解，最后给出同类习题进行训练，练就一双能够洞察问题深层结构的慧眼，以便同学们能举一反三，做一题，会一类，通一片.

1.林群义务教育教科书八年级数学上［M］.北京：人民教育出版社，2012.J