关注数学文化，信息调用探究——以以数学文化为背景的材料探究题为例

☉江苏灌云县九年制实验学校 刘 翠

数学有着悠久的历史，它不仅是一门学科更是一种文化，数学在发展的同时也承载了众多的人文故事、情感文化.近年来中考对数学知识点的考查加强了数学文化的渗透，通过阅读材料与问题探究的融合考查学生知识理解、问题探究的能力，因此有必要引领学生关注以数学文化为背景的材料探究题.

一、真题解析，试题点评

1.真题呈现.

（2017年山西中考卷第22题）背景阅读：早在三千多年前，我国周朝数学家商高就提出：将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三，股四，弦五”.它被记载于我国古代著名数学著作《周髀算经》中.在本题中，我们把三边的比为3∶4∶5的三角形称为（3，4，5）型三角形.例如，三边长分别为9、12、15或的三角形就是（3，4，5） 型三角形.用矩形纸片按下面的操作方法可以折出这种类型的三角形.

实践操作：如图1，在矩形纸片ABCD中，AD=8cm，AB=12cm.

第一步：如图2，将图1中的矩形纸片ABCD沿过点A的直线折叠，使点D落在AB上的点E处，折痕为AF，再沿EF折叠，然后把纸片展平.

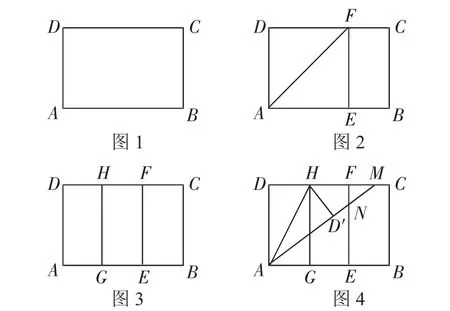
第二步：如图3，将图2中的矩形纸片再次折叠，使点D与点F重合，折痕为GH，然后展平，隐去AF.

第三步：如图4，将图3中的矩形纸片沿AH折叠，得到△AD′H，再沿AD′折叠，折痕为AM，AM与折痕EF交于点N，然后展平.

问题解决：

（1）请在图2中证明四边形AEFD是正方形.

（2）请在图4中判断NF与ND′的数量关系，并加以证明.

（3）请在图4中证明△AEN是（3，4，5）型三角形.

2.试题解析.

分析：（1）略.（2）首先需要理解古书中“勾三，股四，弦五”的具体含义，它表示直角三角形的三边关系，其次理解何为（3，4，5）型三角形，即满足上述三边关系的直角三角形.证明边的关系可以将其放置在特殊三角形中，利用三角形全等证明.（3）求证△AEN是（3，4，5）型三角形，需要求出三边的值，可利用特殊图形和折叠特性得相关条件，设出NF的边长，并表示出其他两边，将其放在直角三角形中，利用勾股定理求解，最后通过三边之比证明.

解：（2）如图5，连接HN.

由折叠知∠AD′H=∠D=90°，HF=HD=HD′，∠EFD=90°，∠ND′H=90°.

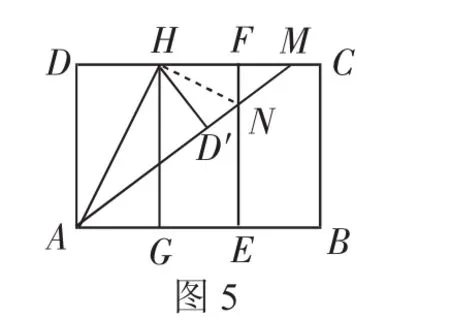
（3）根据四边形AEFD为正方形，可知AE=EF=AD=8cm.

由折叠特性知AD′=AD=8cm.

设NF=ND′=x，则AN=8+x，EN=8-x.

在Rt△AEN中，利用勾股定理解得x=2，则AN=10，EN=6，所以EN∶AE∶AN=6∶8∶10=3∶4∶5，则△AEN是（3，4，5）型三角形.

3.试题点评.

本题是以数学文化为背景的材料阅读、分析探究题，首先给出了“勾三，股四，弦五”的数学渊源，以此为载体开展几何探究，问题的求解充分利用了材料信息，在理解（3，4，5）型三角形的基础上，利用三角形相似及勾股定理进行推理探究.对于以数学文化为背景的材料探究题，需要深入理解材料中的核心概念及相关特性，然后加以有效利用开展问题探究，信息理解是解题的基础，基础知识的调用是解题的关键.

二、试题衔接，思路剖析

以数学文化为背景的探究题的解题关键是理解、运用，即充分理解材料中所陈述的概念、定理、公式，以及相关证明过程，对于公式中的相关符号必须有清晰的认识，理解符号所代表的含义，以此为基础进行深入分析，合理调用材料信息，必要时可以采用数形结合的方式加以分析.

试题1：（2016年凉山州中考卷第24题）阅读下列材料并回答问题：

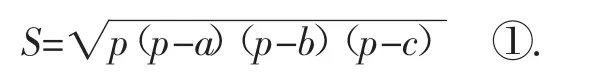
古希腊几何学家海伦（Heron，约公元50年），在数学史上以解决几何测量问题而闻名.他在《度量》一书中，给出了公式①和它的证明，这一公式称海伦公式.

我国南宋数学家秦九韶（约1202—约1261），曾提出利用三角形的三边求面积的秦九韶公式：

这说明海伦公式与秦九韶公式实质上是同一公式，所以我们也称①为海伦-秦九韶公式.

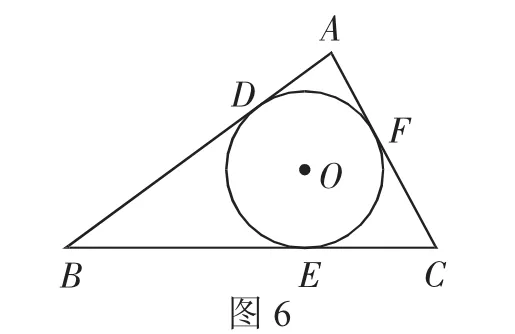
问题：如图6，在△ABC中，AB=13，BC=12，AC=7，⊙O内切于△ABC，切点分别是D、E、F.

（1）求△ABC的面积；

（2）求⊙O的半径.

分析：首先需要理解上述公式所表述的含义，无论是海伦公式还是秦九韶公式，都是利用三角形的三条边长求面积的.第（1）问求面积，利用海伦公式和秦九韶公式都可以，只需将边长代入即可；第（2）问求半径，需要以圆心为公共点，将△ABC分割为几个小三角形，设出半径长，表示出△ABC的面积，利用第（1）问的结论建立方程求解.

解：（1）a=BC=12，b=AC=7，c=AB=13，则p==16.

（2）如图7，连接AO、BO、CO、OD、OE、OF.

⊙O内切于△ABC，设⊙O的半径为r，则OD=OE=OF=r，S△ABC=S△AOB+S△BOC+S△AOC=16r.

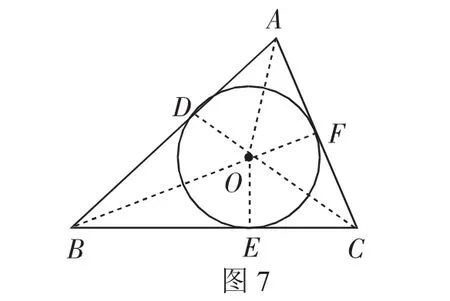
根据第（1）问可知S△ABC=24，即16r=24，解得r=，即⊙O的半径为

试题2：材料：“三等分角”是数学史上一个著名的问题，但仅用尺规不可能“三等分角”.下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法（如图8）：将给定的锐角∠AOB置于直角坐标系中，边OB在x轴上，边OA与函数的图像交于点P，以P为圆心、2OP为半径作弧交图像于点R.分别过点P和R作x轴和y轴的平行线，两直线相交于点M，连接OM得到∠MOB，则∠MOB=∠AOB.要明白帕普斯的方法，请研究以下问题：

（1）略；

（2）分别过点P和R作y轴和x轴的平行线，两直线相交于点Q，请说明Q点在直线OM上，并据此证明∠MOB=∠AOB.

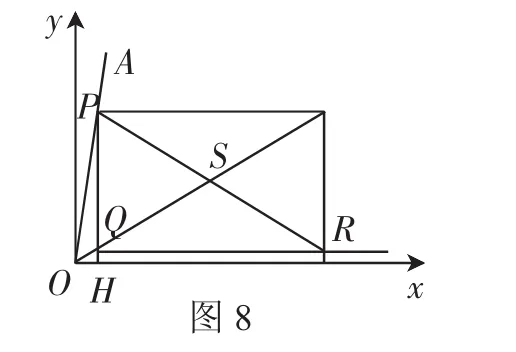
分析：（2）首先需要理解题干所表述的“三等分角”及实现方法，对于证明Q点在直线OM上，只需说明点的坐标满足直线方程即可；证明∠MOB=AOB，需要说明∠POS=2∠SQB，可以根据特殊四边形的性质、外角的特性及直线平行的性质推导转化.

上述问题均为以数学文化为背景的探究题，理解材料信息、合理运用是解题的关键，试题1给出了海伦公式和秦九韶公式，求解过程在理解上述公式是“运用三条边长求面积”的本质上加以展开；试题2则给出了“三等分角”的概念及实现方法，求解过程以此为线索加以应用展开.对信息的理解是解决材料探究题的关键，有效结合几何性质、数形结合可实现问题的简便作答.

三、解后反思，教学思考

1.挖掘阅读材料，感受数学文化.

上述均为以数学文化为背景的材料探究题，无论是“勾三，股四，弦五”的直角特性、海伦公式与秦九韶公式，还是经典的“三等分角”概念，均蕴含着深刻的数学真理，是对数学真善美的充分体现.该类题型对于拓展学生知识面、发展学生的推理能力有着极大的帮助.在教学中应该有意识地引导学生关注教材的阅读材料，深刻挖掘其中的数学文化和应用特性，对其中的定义、概念、定理和公式进行深入学习，让学生体验数学文化博大精深的同时提升自身的创造性.

2.经历探究过程，发展数学思维.

蕴含数学文化的材料题本质上是数学的探究题，是从信息理解到探究应用的过程，该过程体现出知识的形成，而问题的解答需要学生经历理解、观察、猜想、证明等思维过程，同时该题型也折射出中考对于学生探究能力的考查要求，也是未来中考命题的发展方向.教师的思维无法代替学生的思维，照搬硬套只会弱化学生的理解能力，探究题有着较好的价值导向，深入讲解可以使学生达到知识的内化和自省，对于提升学生的思维能力极为有利.

3.依托数学文化，提升科学素养.

中考试题对于数学文化史的引入也反映出中学课程“倡导数学文化价值”的理念，这在每一章节的阅读材料中都有体现.阅读材料是对知识的一个补充和延伸，对学生深刻理解知识的应用价值及体系地位有着重要的意义.将文化史与数学知识点融合讲解，利用文化史的吸引力及情感作用引导学生学习，让学生“因史生趣，由爱到知”，可有效促进学生知识体系的构建，科学素养、人文素养的提升，促进素质教育到教育方针的落实.

四、写在最后

数学文化在试题中的渗透融合开辟了中考命题的新方向，该类问题的解答也需要从理解数学文化所蕴含的概念和公式入手，提取有效信息，开展深入探究，依托文化知识，解决数学问题.对于数学文化的日常教学，需要教师有效把握知识点与数学文化的联系点，深刻挖掘阅读材料的文化价值，通过数学史的讲解使学生充分理解数学知识，构建完整的知识体系，促进学生人文素养的提升，同时关注学生数学思维的培养，让学生亲历探究过程，提升思维能力.

1.杨虎.重视阅读材料挖掘数学文化——从2016年凉山州中考第24题谈起［J］.中学数学（下），2016（9）.

2.邢成云.文化打底素养立意——一道综合与实践创新题赏析［J］.中学数学（下），2017（9）.

3.王新宇.基于数学文化视角的初中数学教学实践［J］.数学教学通讯，2017（23）.

4.白露.例谈数学文化在中学数学教学中的渗透［J］.数学教学通讯，2017（27）.W