多借一缕春风，还你满园芬芳*

☉安徽合肥市包河区教研室 汪洪潮

课堂教学需要教师对教学内容进行深入分析，然后根据学情和经验设计教学方案，最后组织实施教学.然而，不少教师由于对《义务教育数学课程标准（2011年版）》的精神领悟不透，对数学育人的内涵理解不够，对教学内容的本质挖掘不深，从而课堂教学立足于解题应试，忽视对学生进行数学思维的训练.如何改变这种现象呢？现以几个案例说明，只要我们在教学中，立意高一层、问题进一步、机会多一点，我们的课堂就会熠熠闪光，就会变得灵动而有智慧，就会成为培养数学思维的乐园！

一、高立意，培养学生用数学的眼光观察

世界是普遍联系的，数学知识间也是密切联系的.相同知识点有前后逻辑关系，不同知识也可能存在研究方法和套路的一致性.教学中，如果教师能跳出课时内容的局限，站得更高一层，抓住知识间的联系，就能引领学生用数学的眼光认识和观察世界.

例如，在七年级学习“角”一课时，通常教师都是按照教材顺序组织教学，即“观察生活中的角——抽象得到角的图形——介绍角的定义——介绍角的构成元素——角的表示和度量”.这样的安排没有问题，但是对“角”这样一个全新的几何概念，我们应该研究什么？怎样去研究？前面知识的学习有没有帮助？它的学习对后续几何图形的学习有没有借鉴价值？第十届初中青年数学教师优秀课展示活动中，来自江苏南通启秀中学的汪健老师为我们提供了一个很好的案例.

师：前面我们学习了“直线、射线和线段”的有关知识，我们都研究了哪些内容？你能按顺序说一说吗？

生：我们学习了定义、表示、分类，以及线段的度量和比较、线段的和与差……

师：在学习相关知识过程中，都用了哪些方法？

生：有度量法、叠合法、分类讨论、画图说明.

师：角也是一个基本几何图形，请你猜想，我们要研究关于角的哪些内容？

生：估计也要学习角的定义、表示、分类、角的度量和大小比较、角的和与差……

师：可能会用到哪些方法？

生：估计也要用到度量法、叠合法、分类讨论、画图说明.

……

本片段中，教师通过引导学生回顾“直线、射线和线段”的研究历程及研究方法，启发学生思考“角”的研究内容和方法.“线段”和“角”都是基本几何图形，它们的研究内容和方法有内在的一致性，而且这种研究内容、方法及经验也为今后学习其他图形（如三角形）提供了借鉴.这样的教学设计，立意高远，能有效引领学生从整体观视角下审视我们的学习内容，把握几何学习的基本方法和套路，对后续学习具有奠基作用.

二、深追究，引领学生用数学的思维思考

数学课堂教学，教师往往通过问题引领学生思考，通过层层递进、有挑战性的问题，调动学生的思维，向知识的根源和本质探索.问题的质量影响学生思维的参与程度，好的问题，犹如一把钥匙，引领学生步入数学理性思维的殿堂.

在沪科版九年级下册“圆的基本性质”一课中，教材上有如下例题，目的是巩固和应用圆的有关性质.

例 已知：如图1，AB、CD为⊙O的直径.

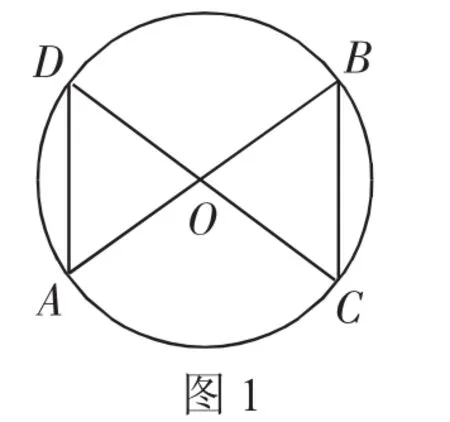
求证：AD∥BC.

本题难度不大，解决方法多样，学生往往采用三角形全等或平行四边形的有关知识进行解答.但解答之后，总感觉意犹未尽.本题在巩固和应用新知方面比较简单，而图形所蕴含的圆的基本性质没有挖掘，学生思维的层次不高.为提升思维含金量，做如下引申：

（1）弧AD与弧BC相等吗？

（2）任意矩形的四个顶点是否一定能在同一个圆上？为什么？

问题（1）引领学生思考如何证明弧相等，根据定义“在同圆或等圆中，能够完全重合的两段弧叫作等弧”，因此，启发学生思考如何将两段弧重合，从而调动学生利用圆的轴对称性质或旋转不变性质进行证明.

问题（2）既是对圆的定义的巩固，更是为“如何证明四点共圆”提供一种思路.将矩形从圆中抽取出来，引导学生进行逆向思维，不仅可以巩固“点和圆的位置关系”，也为后续学习“四点共圆”提供了范例.

有这两个问题的引领，思维的含金量陡然增加.通过问题的解决，学生学会抓住图形的本质特征，通过正反两个角度分析问题，学生在问题解决的过程中学会思考.

同样在沪科版八年级上册“轴对称图形”一课的教学中，教师布置如下问题：

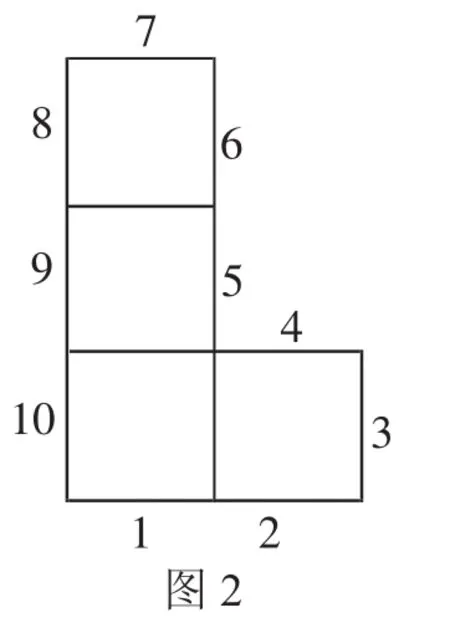
如图2，由4个边长为1的小正方形拼成的图形，请在图中再增加一个同样大小的小正方形，使之构成轴对称图形，共有几种不同的摆法？

生：共有3种摆法.（然后上黑板一一指出）

教师肯定其答案正确后，就进入了下一教学环节.

本题难度不大，很多学生都能数出来.但教学时，我们不能“就题论题”，应该从题目中发现方法，寻找规律.如果教师按如下方式教学，那么立意和品位就会高很多：

师：你是如何思考的？怎样才能保证不重复、不遗漏呢？

师：原图周长为10（如图2，为方便分析，每条小正方形的边依次记为1～10），添加的小正方形的一边依次与原图形的每一条边重合，共有9种摆法（其中与边4和边5重合时重复了），其中能够组成轴对称图形的共有3种（即与边3、边6、边10重合时）符合条件.

师（进一步追问）：如果添加两个小正方形，使之构成轴对称图形，又有几种摆法呢？该怎么思考呢？

虽然此题的答案很容易得到，但教学时，我们要淡化结果，重视分析问题的方法和过程，如果教师能够通过这个问题，将解决“如何有序摆放”的方法揭示出来，对后续解决“有序思考”的问题很有借鉴意义，学生的数学思维在此过程中得到锻炼和提高.

三、多放手，训练学生用数学的语言表达

当前，很多教师认为，数学教学的目的是学生会解题，考试得高分，忽略了对学生动手和动口能力的培养，教学停滞在“学生只要会做或能做对就行了”的较浅层次上.引导学生学会“用数学的语言表达和交流”是数学学习的主要任务之一，如何“培养学生用数学语言表达世界”是每位教师应该重点关注的问题.

如何训练学生的数学语言表达能力呢？沪科版七年级上册“线段的长短比较”的教学片段给我们很好的启示：

师：前面我们学习了直线、射线和线段的有关知识，我们知道直线和射线是不可度量的，而线段是可以度量的，也就是说线段是有长短的，今天我们就来学习线段的长短比较（揭示课题）.其实，我们生活中就有类似的比较，如比较甲、乙两个同学的身高，你会吗？

生：两个同学站在一块，背靠背站立进行比较.

师：为什么要背靠背？

生：保证两个人是竖直站立的，这样才公平.

师：如果两个同学一人站在台阶上，一人站在地面上，这样背靠背比较行吗？

生：不行，必须两个人站在同一平地上，然后背靠背比较.

师：甲、乙两个同学按要求站好了，怎么得出谁高谁低？

生：如果甲的头比乙的头低，就说明甲比乙矮.

师：如果把甲、乙两同学的身材分别看成线段AB和线段CD，“甲的头比乙的头低”这句话是什么意思呢？

生：甲、乙两个同学的脚分别相当于线段的一个端点A和C，而头则分别是另一个端点B和D，“甲的头比乙的头低”这句话就是说“线段AB的端点B在线段CD上”.

师：你能结合甲、乙两人身高的比较，说说如何比较线段AB和线段CD的长短吗？

生：“背靠背”就是说两条线段要叠合在一起（即在同一条直线上）；“站在同一平地上”，说明线段的一个端点要重合.谁长谁短就看第二个端点的位置了.

师：两条线段长短的比较，有几种可能呢？

生：点B落在CD之间（即端点C、D之间），AB＜CD；若点B与点D重合，就说明AB=CD；如果点B在线段CD的延长线上，则AB＞CD.

师：非常好，我们从比较身高的方法中，总结出线段长短比较的方法.

……

本片段，教师紧紧抓住“比较两个同学身高”的情境，启发学生思考：如何比较身高？注意事项是什么？这些方法和注意事项转化到线段长短的比较又是什么？如何用数学语言表述出来？最后总结归纳出线段长短比较的方法.

学生通过不断修改和完善，逐步学会了用规范和严谨的数学语言进行表达与交流，在此过程中，数学的逻辑性和严密性得到很好的体现.

数学是思维的科学，我们要通过对概念的学习、规律的探索、定理的推导、问题的解决等途径训练学生的思维，培养他们的理性精神.只有深刻理解数学知识间的逻辑关系，准确把握教学内容的本质，充分挖掘题目中蕴含的数学思想方法，大胆放手让学生尝试与探究，才能使我们的课堂达到“高立意、高品位”，最终实现“数学育人”的目标.W