对话教学模式下的有效课堂

☉南京师范大学附属中学仙林学校初中部 曹玉梅

众所周知，数学教学有很多模式，启发式、探究式、建构式等等，不断影响着中学数学的教学.可以这么说，任何一种方式都不可能完美地解决所有的课堂教学内容.大量的教学资料显示，教学课程改革初期所提倡的建构式教学模式，随着教学的改革的深入渐渐不再那么被热衷了，原因很简单，这种理论强于实际操作的教学模式，在当下的数学课堂教学中难以实现.

随着课堂教学的改革趋于理性化，我们不难发现回归传统的教学才是符合当下教学实际的.笔者以为按照现今教学的程度和难度来说，对话式、启发式等教学模式是比较符合现在的课堂教学的.原因很简单，人民教育出版社章建跃博士这样评价现在的课堂教学：很多华而不实的教学模式渗透在今天的课堂教学中，让教学呈现一种脱离数学的华丽，但是对于数学知识的理解和掌握却没什么推动作用，反而中学数学传统的启发式、对话式等让教学来得更为平易近人、符合学情.本文以对话式教学为本，跟读者一起聊一聊如何在教学中做好对话式教学的设计并实施对话式教学.

一、概念教学中的对话

概念教学是需要对话的，因为数学概念是极为抽象的、形式化的一种数学结论.对于中学生而言，其思维的发展程度尚不能达到概念的完全建构程度，因此需要教师合理地设计概念教学流程、设计启发过程、设计对话引导，将数学概念中的难点，通过对话的方式加以理解和运用，从而获得教学的有效性.

案例1 八年级上《认识函数》一课概念教学对话设计.

师：大家都听过函数一词，那么到底什么是函数呢？

生：就是y和x的表达式吧.

师：这么说对不对呢？我们还是从几个生活中的例子来看一看.图1是加油站加油表，也是生活中大家常常见到的，请问你能从中获得什么样的信息呢？

意图：这段对话设计的意图是暗示学生，生活中无处不用数学，其中蕴含的函数关系一直下意识地存在于学生头脑中.

生：加多少升油和总金额之间的关系，如表：

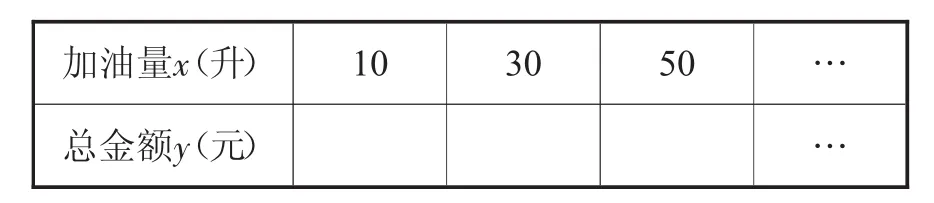
师：好！同学们设计的这个表格，是很明确的一种对应关系.你认为是什么关系？

意图：让学生感受变量和变量之间的关系，目的是为后续函数关系的真正界定打下基础，即函数是研究变量之间的一种特殊对应的关系.

生：是一种函数关系吧！

师：同学们确定吗？应该这么说，这是一种对应，也是一种函数.不是所有的对应关系都是函数关系，但所有的函数关系都是对应关系.后续对这一概念再进行说明.现在你能提出相关的一些关于加油的问题吗？

生：如果我某次加油的金额是180元，试问这次加了多少油？

意图：再一次请学生感受函数关系，这种关系是以定量的方式呈现的，让学生通过存在于自己知识体系中的认知，对函数关系有一个初步的认识.

师：你能用含有加油量x（升）的关系式来表达加油总金额y（元）吗？

生：可以，y=5.49x.

师：这是一种对应关系，也是一种函数关系.我们对变量和变量间的关系有了最为直观的案例认识，后续我们将进一步介绍函数的概念.

意图：这段对话是明确告诉学生，这样的变量和变量之间的关系是一种函数关系，为后续介绍函数概念和进一步认识函数关系奠定基础.

这一案例是认识函数，因此就函数关系进行深度认识交流，教师的对话主要是与学生一起进行函数关系的初探，研究变量间的关系.这里的对话设计，是教师合理引导、步步为营，引导学生向函数关系靠拢的典型尝试.

二、解题教学中的对话

解题教学是中学数学的重中之重，对于初中生而言，其对于解题的认识自然是比较浅显的，即就题论题式的解题占据大多数学生的主要意识.笔者以为，学生在解题训练中获得的提升之所以缓慢，与教学未能做到举一反三有重大关系，因此笔者建议要对解题教学进行多变的引导、多变的对话，将知识的本质真正在解题教学中运用到位.

案例2 若3a2-8a+1=0，b2-8b+3=0，ab≠1，求的值.

分析：本题是数学竞赛辅导课上，笔者给出的一个求根问题.对于问题的解决，采用对话的方式步步引导，和学生一起探讨解决的方式.显然问题有一定的难度，因此笔者设计了铺垫，对学生进行逐步对话引导.

引导1 若实数a、b是方程x2-7x+2=0的两个根，则式子的值是______.

师：引导1，同学们怎么思考？

生：可以将这两个根求出来，再进行计算.

师：这种方式固然可以，但并非最优的方式，还可以怎么处理更为优化？

师：不错，第二种方式显然提高了思维的含量，将根与系数的关系运用到位.

意图：通过引导1复习回顾一般问题的常规解决方式，回顾回顾根与系数的关系.

引导2 若a2-7a+2=0，b2-7b+2=0，且a≠b，则式子的值是______.

分析：将同一问题用不同的形态展示，用不同的表象展示出来，加深问题本质的理解.

生：跟上面的问题是一样的，即a、b是方程x2-7x+2=0的两个根，转化为上面的问题即可.

引导3 若a2-7a+2=0则式子的值是______.

分析：继续改编问题，渗透数学思想到具体的问题中.

师：再看引导3，你如何处理呢？

师：很好！在引导2的基础上，我们发现只要结合整体思想，不难实现问题的解决，问题又回归到了我们熟悉的模型.

意图：通过数学思想的渗透，对问题的难度实现了逐步提升.

引导4 若a2-7a+2=0，2b2-7b+1=0，且，则式子的值是______.

师：同学们思考，本题与前面问题的区别在哪里？你如何解决？

师：漂亮！说明同学们解决问题的整体思想又往前了一大步，从方程的结构特征入手，我们不难发现a和是方程x2-8x+3=0的两根，这里整体思想非常重要，因此韦达定理的介入可以轻松地解决问题，课后大家再具体试一试，答案是.最后回归案例2，同学们认为怎么样？

生：若3a2-8a+1=0，b2-8b+3=0，ab≠1，求的值.不难发现，本题不就是引导4吗？问题本质跃然纸上，因此很容易解决了.

通过教师的设计和对话，将问题以分步求解的方式呈现出来，给予学生问题解决的本质展示.此处教师的设计是合理的，以教材基本问题的解决为契机，将不同的问题表征和思想渗透融合在一起，实现了知识的更真实的理解，达到了更有效的课堂教学效果.

三、实验教学中的对话

数学实验是中学数学较为新颖的数学实践活动.但是数学实验往往需要在教师的引导下去实践这一过程，实验教学中对话的主要作用在于引导学生如何实现数学软件等一系列的操作，限于篇幅笔者举一个简单案例说明.

案例3（动态试验）利用现代信息技术教育功能，从动态变化中研究函数问题.如研究二次函数相关问题：函数y=x2-2mx+8在-1≤x≤1内最小值为1，求m的值.

分析：利用信息技术，实现动态过程，通过对话教学实现问题的解决.

师：利用几何画板，设置参数m，现在实现参数的运动，我们观察这一过程中，在-1≤x≤1内最小值有几种可能性？

生：观察动态变化，我发现有三种情况，如图2.我用几何画板也尝试了下，发现最值和对称轴的变化有关系.

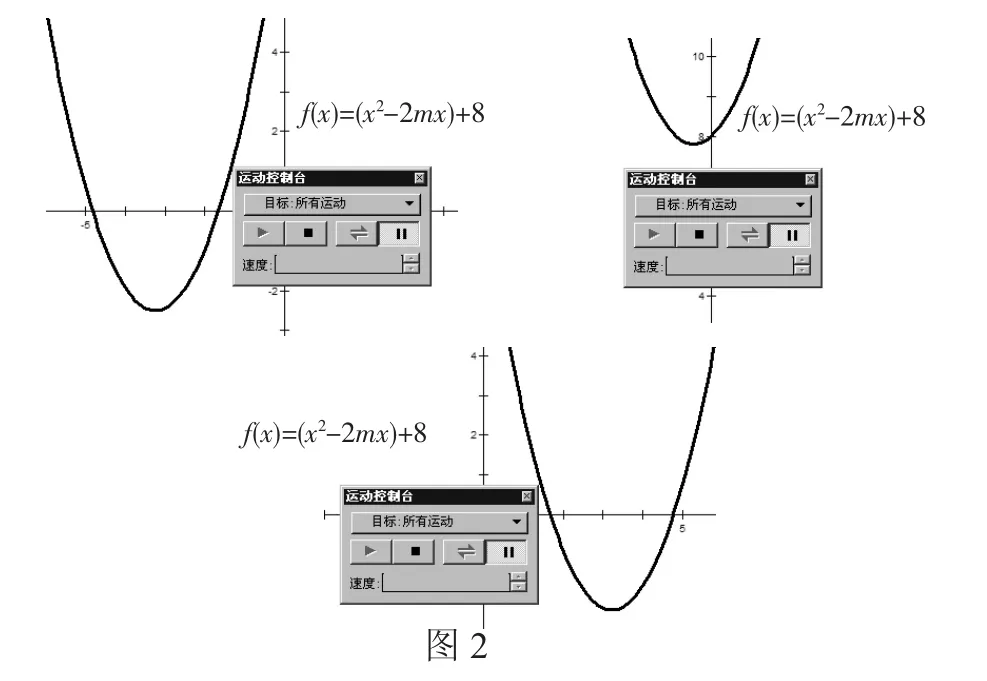
师：怎么分类？

生：当对称轴小于-1时，显然在-1≤x≤1内的最小值在x=-1处取到；随着对称轴向右移动，-1≤x=m≤1，则在-1≤x≤1内的最小值在x=m处取到；随着对称轴继续向右移动，x=m＞1，则在-1≤x≤1内最小值在x=1处取到.

师：很好，实验对我们解决问题有非常直观的作用.

总之，好的教学离不开教师的引导，教师的引导恰恰是通过对话实现.这种对话的实现需要教师的设计和遵循学生最近发展区的语言引导，将形式化的数学问题和过程，以非形式化的过程进行展示，加深学生的理解、提高教学的效益、实现有效的课堂教学.

1.章建跃.普通中学新课程数学教学实施回顾与展望［J］.中小学数学，2013，2.

2.王俊.关于学习反思的几点思考［J］.中学数学（下），2003（1）.

3.梁旭.教师教学能力案例分析——数学解题能力的差异［J］.中学数学教学，2011，7.J