课本题，巧设计，出新意——一道期中原创题的命制过程及感悟

☉苏州市吴江区笠泽实验初级中学 庄佩玉

教材——经过专家多次打磨、筛选后的精品，它是命题的蓝本，也是命题的良好素材，是考题的主发源地，可谓取之不尽、用之不竭，每年期中、期末考试都有大量的题目直接出自教材，或以教材例题、习题为基础，改编设计、繁衍生息.教材中的诸多例题、习题蕴藏着丰富的潜在功能，故作为命题重要的资源库，这些题目有待我们把握立意，探索其根源，探究其变化.同时，《义务教育数学课程标准（2011版）》明确指出：评价的主要目的是全面了解学生数学学习的过程和结果，激励学生学习和改进教师教学.所以，教师上课用好教材去教学，命题者用好教材去改编试题，都是相当重要的.近期，笔者命制了本区九年级上学期期末考试试卷，压轴题以一道课本习题入手，将其推广、延伸，得到了全区老师的称赞.命题过程中有些许心得，故撰文与同行分享.

一、原题呈现

（一）问题提出

苏科版《数学》九年级（上册）习题2.1有这样一道练习题：

如图1，BD、CE是△ABC的高，M是BC的中点．点B、C、D、E是否在以点M为圆心的同一个圆上？为什么？

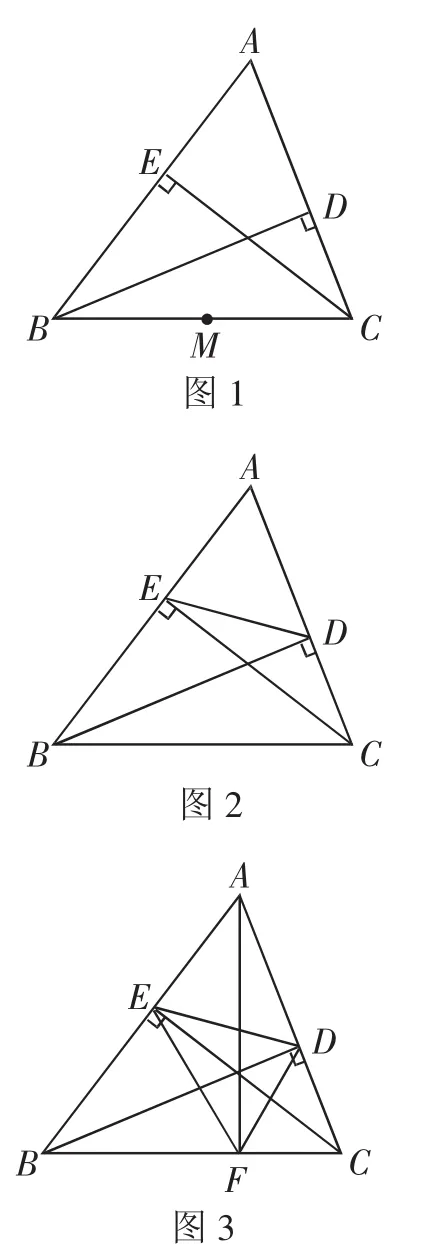
在解决此题时，若想要说明“点B、C、D、E在以点M为圆心的同一个圆上”只需证明______.

（二）初步思考

如图2，BD、CE是锐角△ABC的高，连接DE.

求证：∠ADE＝∠ABC.

小敏在解答此题时，利用了“圆的内接四边形的对角互补”进行证明.

（请你在下面的空白处根据小敏的思路完成证明过程）

（三）推广运用

如图3，BD、CE、AF是锐角△ABC的高，连接DE、EF、FD.猜想∠EFB与∠DFC之间存在的关系，并说明理由.

分析：本题是典型的“推广运用型”试题.题目选自课本习题，以“探究四点是否共圆”为载体，继而逐渐复杂，再经过巧妙铺垫，给出思路让学生补充完整，最后通过已获得的经验解决问题.本题涉及的知识点看似单一，实则内涵丰富，解决此题需要极高的应用意识.本题特别注重思想方法的考查，蕴含了转化的思想.题目共三问，由简入难，在问题的设置上注重螺旋式上升，环环相扣，第一问为填空题，比较容易，旨在让学生掌握本题的核心解题方法，考虑到本题是压轴题的定位，学生可能充满畏惧感，所以第一问尽可能降低难度；第二问为证明题，但给出了思路，降低了难度，只要学生发现第一问和第二问的联系，题目便可迎刃而解；第三问难度大大上升，图形虽然类似，但问题却有很大差异，实则密不可分，此问旨在让学生经历分析问题、解决问题的过程，特别注重考查用发展的眼光看问题，让学生尝试将陌生问题转换成熟悉问题，从而解决问题，此问区分度明显，综合性很强.

二、命题过程

（一）初定方案

各地中考题的压轴题常考两大类题目：“推广运用”型试题、“新定义”型试题.由于命题时间有限，“新定义”型试题的命制有一定的难度，所以笔者决定考查“推广运用”型试题.这类试题立意鲜明、设问灵活，让学生从已有经验出发，加以运用，从而解决类似问题.确定题型后，便要思考考查的内容，由于此次考试是九年级上学期，主要考查四章的内容：一元二次方程、圆、统计、概率.通过多年命题的经验及对这四章重要性的把握，笔者决定此次期末试卷的最后一道压轴题以圆为载体进行考查.

确定了题型和考查内容后，笔者翻阅了书本，这一章涉及的知识点众多，可大致分为三块：点与圆的位置关系、直线与圆的位置关系、图形与圆.由于直线与圆的位置关系、图形与圆是经常考查的压轴题，为了能有一些新颖之处，笔者初定以点与圆的位置关系为载体进行考查.基于压轴题的定位，笔者决定命制一道难度系数为0.3～0.4的“推广运用”型试题，题目预设2～3问，逐步递进，主要以推广运用为考查方式，让不同层次的学生都可以得到适合自己的分数，又能让优秀的同学凸显出来.

（二）形成初稿

计划拟定后，笔者翻阅教材，打算寻找适合的出题资源.苏科版《数学》九年级（上册）习题2.1有这样一道练习题吸引了笔者的注意.

如图4，BD、CE是△ABC的高，M是BC的中点.点B、C、D、E是否在以点M为圆心的同一个圆上？为什么？

此题以四点共圆为载体，这是一个重要的结论，但又是考试经常回避的问题.第一稿时，笔者打算让学生通过此题直角三角形研究四点共圆的问题，让学生推广到非直角三角形四点共圆的研究，但仔细思考后，决定还不能这样出题，否则有违近几年本地中考的命题思想.再三斟酌后，笔者决定以这道题推广开，在基本图形的基础上让学生通过运用得到更多的结论.

（三）完善修改

作为学生，怕压轴题，对这类题存在很大畏惧感，本着设身处地为学生考虑的原则，笔者思虑再三，决定该题无论如何设置都应该一开始易上手，故在第一问设置时尽可能降低难度，第二问设置时进行了适当的铺垫，这样更容易得分，于是第二问设置为“补充型”解答题，给予了适当的提示，让学生有一定的思路.

从考查形式上看，本题是“推广运用”型试题，有填空，有解答，有足够的探索，也有充分的运用，形式比较全面；从考查内容上看，本题以考查四点共圆为载体，融入圆、三角形的相关知识，将中考的核心考点紧密相连，题目特别注重对基础知识、基本技能的考查，也注重对数学思想的考查；从考查意义上看，本题考查的知识连贯性很强，将圆、三角形这两大考点紧密相连，提醒教师授课时需要关注知识间的关联.无论是信度、效度，还是区分度、可推广性此题均是一道不可多得的好题.

三、命题感悟

命题，越来越受到更多教师的重视，这不仅关乎着教师教学时对各知识点的把握能力，更关乎教师对题目研究的能力水平.很多教师对命题总感觉无从下手，不知如何命题，尤其是命制一道好题.对于期中、期末考试这种大型的区域性考试很多教师更感觉命题的困难，由于部分教师命题能力的有限，常常将陈题拿来或者简单改编，这样的做法会把广大备考师生引向题海，让教学导向彻底走偏.

只要掌握方法，命题并非一件难事.当然平时是需要积累的，多思考就会有收获.试卷中的题型大致可以分为容易题、中等题和较难题.容易题在一份试卷中约占70%，这类题主要检查学生对知识掌握的程度，以考查基础知识和基本技能为主，如求二元一次方程组的解、证明三角形全等、列树状图或表格求概率等，这类题注重考查学生对知识所蕴含的数学本质的理解，题目较为单一，可以用一些陈题改编，更换背景即可；中等题在一份试卷中约占20%，这类题的作用是区分开一部分学生，以考查学生对数学知识的理解程度为主，如圆的部分考题、二次函数的部分考题等，故此类题需要一些创新；较难题在一份试卷中约占10%，这类题主要选拔出部分好学生，检测学生对数学知识是否融会贯通，故建议原创，这样才能公平、公正地检测出学生学习的过程，同时指出教师教学过程中存在的相关问题，为备考师生指明日后正确方向.无论哪一类题，命题时都要淡化技巧，多去体现通性、通法，当然，实在想不出好题时，可以从课本中找素材，切勿出现偏题、怪题，常常可以通过更换背景、类比迁移、横向迁移、纵向迁移等方法进行命题.

命题，对有些人简单，对有些人困难.教师想把题命好，这一定是一个长期的过程，要注重在教学的过程中去收集素材，在命题前深入的研究，命题后再去反思总结.这样，命题的水平才能提升.所以，多在小的问题、熟悉的模型中去寻找突破口，多思考，把握住任何一个可以突破的机会，让命题真正超值、教学真正行之有效.J