动态改变惯性权重的新模式粒子群算法

杜 江，袁中华，王景芹

(河北工业大学 电磁场与电器可靠性省部共建重点实验室，天津 300130)

近年来，各种智能仿生算法相继被提出，1995年由Kennedy等[1]等提出的粒子群算法(particle swarm optimization，简称PSO)便是其中一种.粒子群算法是对鸟群和鱼群捕食行为进行抽象模拟的一种群智能优化算法，具有结构简单、参数个数少、鲁棒性强等优点，一经提出便在计算机领域和许多工程领域得到广泛应用[2-8].

然而，与其他智能算法一样，粒子群算法也存在易陷入局部最优、收敛精度不高、收敛速度较慢和收敛成功率低等问题.针对这些不足，国内外学者进行了大量的研究与改进.文[9]提出一种新的控制惯性权重的方法，控制过程简单、易实现，但对算法性能的提升非常有限.文[10]根据每个粒子的适应度值自适应地改变每个粒子的速度权重，动态调整每个种群粒子的活性，提高了算法的全局寻优能力和收敛能力，但收敛速度却有所下降.文[11]引入了动态跟踪邻域项，改进了惯性权重和学习因子的调整策略，显著提高了算法全局收敛性能.文[12]将混合蛙跳算法中的排序和分组机制引入简化粒子群算法中，提高了算法的求解精度，同时降低了算法收敛于局部最优解的可能性.

论文针对标准粒子群算法的不足，通过实时调整惯性权重和粒子飞行路线，构建了一种新的改进的粒子群算法(particle swarm optimization algorithm with dynamically changing inertia weight，简称DMPSO).通过4个标准测试函数对改进后粒子群算法的性能进行测试，证明了改进算法求解复杂优化问题时具有更高的求解精度和求解成功率.

1 标准粒子群算法

粒子群算法是一种群智能优化算法.假设粒子群由m个分布在D维空间的粒子个体组成，每个粒子个体的属性均包含3个D维矢量：xi=(xi1,xi2,…,xiD)、vi=(vi1,vi2,…,viD)和pi=(pi1,pi2,…,piD)，其中xi、vi和pi分别为粒子i在解空间内的位置、飞行速度和历史最优位置，且1≤i≤m.pg=(pg1,pg2,…,pgD)为整个粒子群搜索到的最优位置.算法迭代过程中，每个粒子的位置按式(1)、(2)进行更新

(1)

(2)

算法以适应值的大小判断其位置的优劣，每次迭代均更新每个粒子的当前位置、历史最优位置和整个粒子群搜索到的最优位置.

2 粒子群算法的改进

2.1 惯性权重的改变

惯性权重w是PSO算法最重要的参数之一.由公式(1)很容易看出，w的大小决定了粒子上次迭代中飞行速度对本次迭代中飞行速度的影响，即决定了全局和局部搜索能力.分析可知，w取较大值有利于全局搜索，但增大算法开销，降低算法效率；w取较小值有利于局部搜索，加速算法收敛，但容易陷入局部最优.所以，设置一个合适的w可以平衡全局和局部搜索能力，即兼顾算法收敛速度和收敛精度，降低陷入局部最优解的可能性，提高算法的整体性能.

关于如何实时控制w的大小，国内外学者进行了大量研究.文[13]提出线性减小惯性权重的方法(linearly decreasing weight, 简称LDW)，如下式

(3)

其中：wmax、wmin分别为惯性权重的最大和最小值，die为当前迭代次数，DIE为最大迭代次数.

LDW方法控制直接、实现简单，但因为对w的调整只考虑了算法所处的迭代阶段，所以很难适应复杂、非线性问题的求解，对标准算法性能的提升非常有限.

事实上，想要减小求解复杂问题时算法陷入局部最优的可能性、提高收敛精度和收敛成功率，除了要考虑算法所处的迭代阶段以外，还应该考虑迭代过程中粒子的分布情况(集中或者分散)，即w的大小应由迭代阶段和粒子分布情况共同决定，如下式

(4)

其中：α为惯性权重变异算子，它的大小由粒子在解空间内的分布情况决定；其他参数的含义与式(3)一致.

考虑实时检测解空间内粒子的分布情况，论文采用文[14]提出的分布熵来表示，如下式

(5)

其中：k=1,2,…，Q，m为粒子个数，Q为解空间被平均划分的相等区域的个数，m1、m2、…、mQ分别为第die次迭代后每个区域内的粒子个数.

E(die)越小说明粒子越集中，此时应为α赋一较大值，即加强全局搜索；反之，E(die)越大说明粒子越分散，此时应为α赋一较小值，即加强局部搜索.α的具体调整方法如下式

(6)

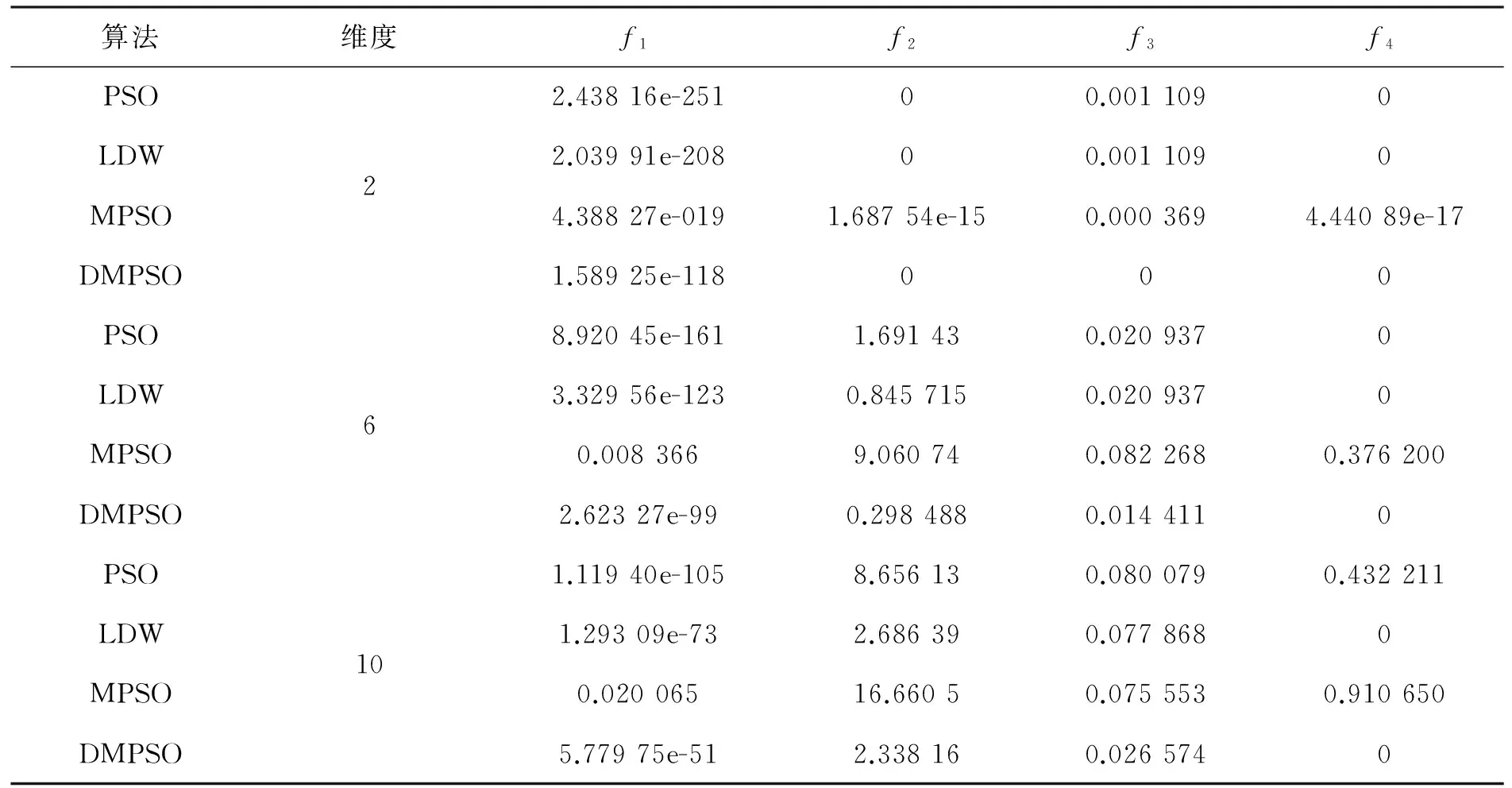
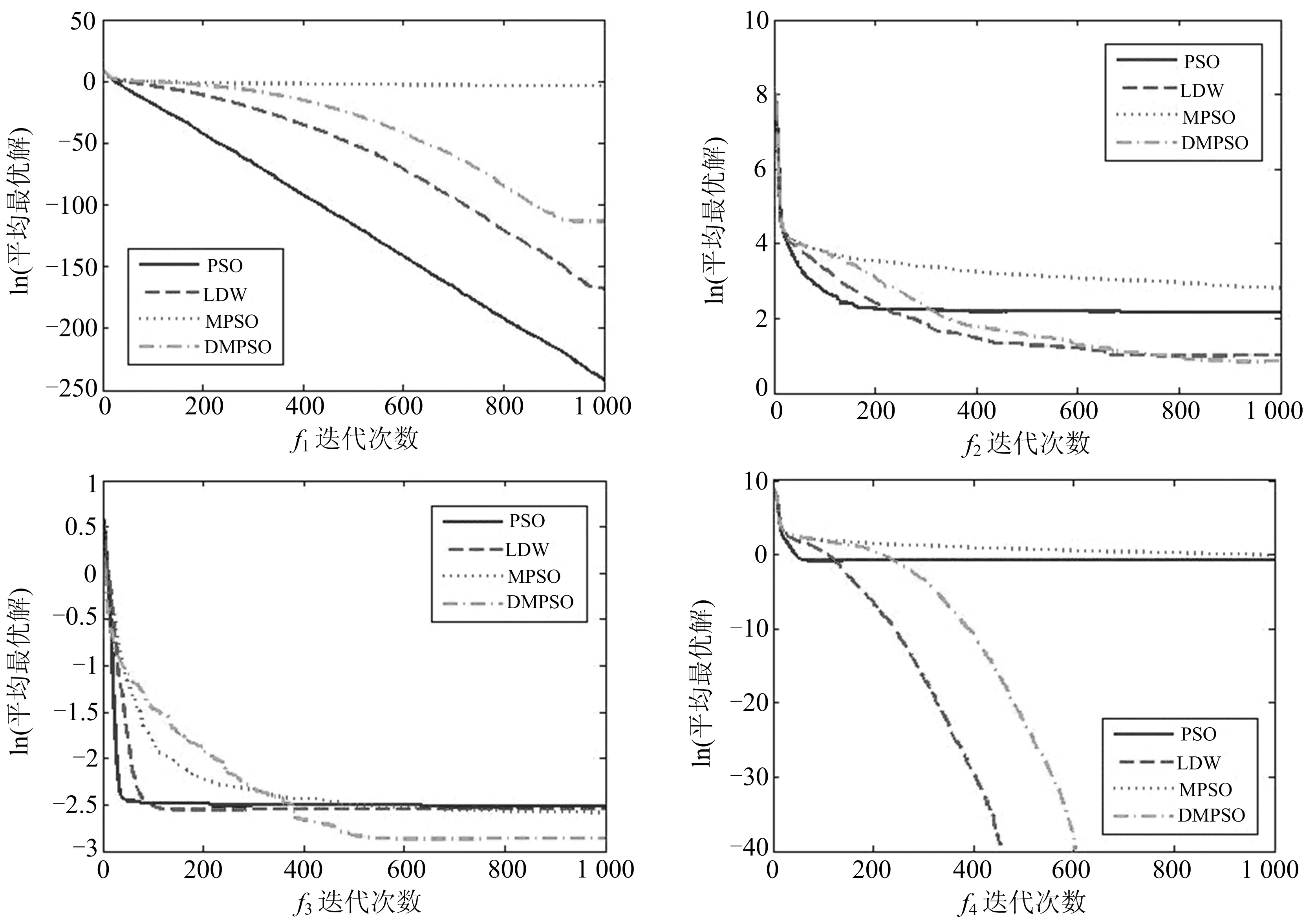
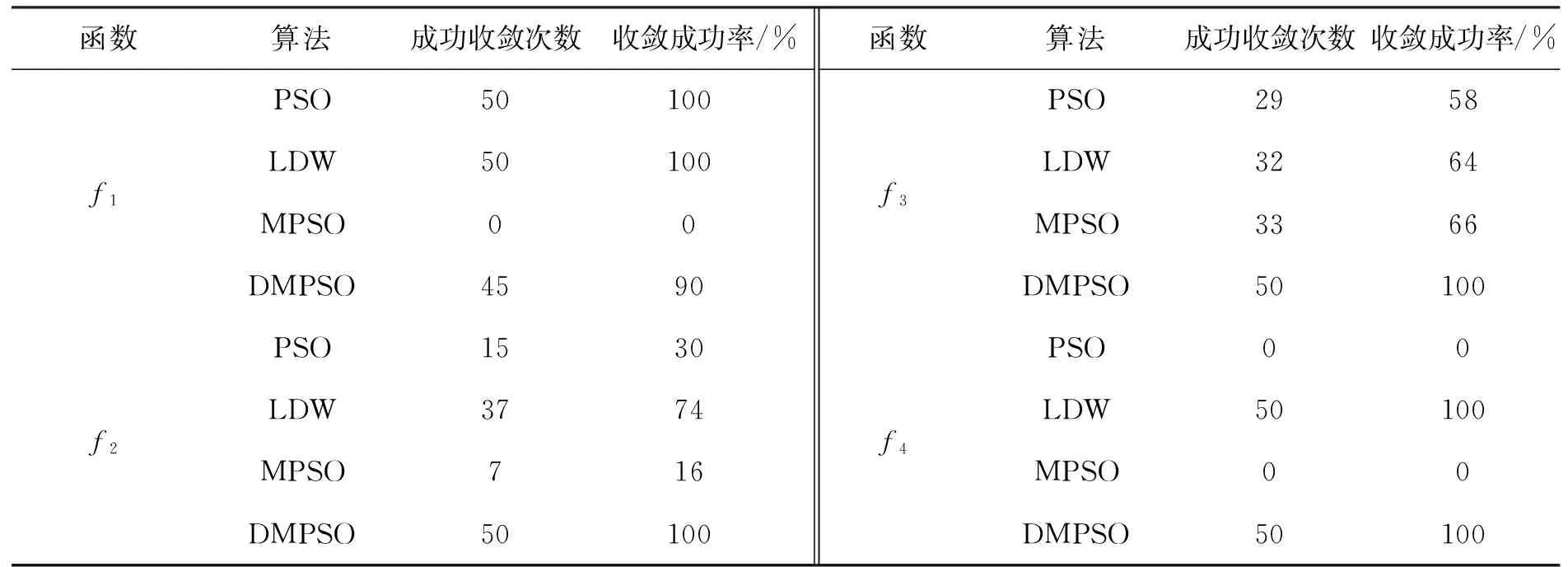
其中：E1、E2分别为粒子分布熵的上、下门槛值(应满足E1

在算法迭代后期，粒子势必会集中于全局最优解附近，此时增大α来加强全局搜索势必会影响算法最终的收敛性.所以，以分布情况调整w大小的方式仅适用于算法迭代前期和中期，即die

2.2 飞行模式的调整

合理地控制w的大小，可以改善算法的性能，除此之外，效仿其他智能优化算法，合理利用种群其他粒子的经验，无疑也可以从中受益[15].分析可知，每个粒子的历史最优位置pi的附近出现全局最优解的可能性要远远大于其他位置(特别是在算法迭代中后期)，当某一粒子连续多次不能更新其历史最优位置pi时，由式(2)可知，该粒子很有可能已经远离了其历史最优位置pi，继续迭代进而得到更优解的可能性非常小，此时应该将该粒子 “拉回”其历史最优位置pi处，以其历史最优位置pi处为起点继续飞行，即把式(2)修改为式(7)

(7)

此时种群其他粒子的状态(历史最优位置)已经改变，加之算法本身的随机性，所以，被“拉回”的粒子不会延续上次“失败”的路线飞行.综上所述，如此调整之后减小了粒子搜索的盲目性，增加了粒子搜索到全局最优解的可能性.

2.3 改进后的算法流程

改进后的粒子群算法流程描述如下：

步骤1初始化，包括随机初始化每个粒子的位置xi、飞行速度vi、历史最优位置pi、全局最优位置pg；

步骤2计算每个粒子的适应值；

步骤3更新每个粒子的历史最优位置和种群最优位置；

步骤4根据式(4)～(6)调整惯性权重w；

步骤5若某粒子连续s次不能改变其历史最优位置pi，且当前迭代次数die

步骤6判断算法是否满足结束条件，即是否达到最大迭代次数或满足最小误差：若否，则跳转至步骤2;若是，则结束迭代并输出优化结果.

3 仿真实验

3.1 实验设计

为了测试改进算法的有效性，对4个标准测试函数进行仿真试验，并与标准粒子群算法(PSO)、文[13]提出的线性减小惯性权重的方法(LDW)、文[9]提出的调整惯性权重的方法(MPSO)相对比.4个测试函数的名称、表达式等信息如表1所示.其中：f1为单峰函数，f2、f3、f4为多峰函数.

实验的硬件环境为：Windows XP系统，AMD双核2.5 GHz CPU，1.94 G内存.通过VC++软件进行仿真实验.在试验中，粒子个数m=50，c1=c2=2，惯性权重最大值wmax=0.7、最小值wmin=0.1，分布熵下门槛值E1=2、上门槛值E2=3.2，最大迭代次数DIE=1 000，粒子分布检测结束标志P=0.8.

实验从3个方面进行测试[16]：

(1) 固定算法进化代数，根据多次实验的平均最优适应值比较4种算法的求解精度；

(2) 通过多次试验的平均进化曲线比较4种算法的收敛速度；

(3) 固定收敛精度，比较4种算法的收敛成功率.

表1 测试函数信息

3.2 仿真结果及分析

3.2.1 算法求解精度对比

每一种算法对每一个测试函数在不同维度下均进行20次仿真试验，表2给出了20次试验的平均最优适应值.

由表2可以看出，在简单问题(单峰函数f1)求解时，LDW、MPSO(new model particle swarm optimization)和DMPSO的求解精度均低于PSO，这是因为改进后算法通过对惯性权重的调整，使之更侧重于全局搜索，而在一定程度上削弱了局部搜索.在复杂问题(高维度多峰函数f2、f3、f4)求解时，DMPSO与其他3种算法相比，具有更高的求解精度.

表2 各函数在不同算法、不同维度下的平均最优适应值

3.2.2 算法收敛速度对比

每一种算法对每一个测试函数进行20次仿真试验，得到1 000次迭代平均最优适应值数据，绘制平均进化曲线如图1所示.其中：横坐标代表算法迭代次数，纵坐标代表迭代过程中每一代的平均最优解.同时为了较直观地展示各算法的迭代趋势，对其迭代数据取自然对数.

图1 各测试函数平均收敛曲线

由图1可以看出，在大多数优化问题中，DMPSO的收敛速度仅仅高于MPSO而低于PSO和LDW，这是加强全局搜索能力的必然结果.另外，图1也显示出了DMPSO在复杂问题(高维度多峰函数f2、f3、f4)求解时，具有求解精度方面的优势.

3.2.3 算法收敛成功率对比

设定算法收敛精度如表3所示.其解空间维度D=10.

表3 各测试函数收敛精度

每一种算法对每一个测试函数进行50次仿真试验，迭代次数达到1 000次时仍未达到指定收敛精度，则认为此次试验没有收敛.记录收敛成功次数，并计算收敛成功率如表4所示.其中：收敛成功率=收敛成功次数/50.

表4 各测试函数收敛成功率

通过表4可以看出：相对于PSO、LDW和MPSO，DMPSO在简单问题(单峰函数f1)求解时，其收敛成功率不具有优势；而在复杂问题(高维度多峰函数f2、f3、f4)求解时，收敛成功率明显高于其他3种算法.

综上所述，论文改进的粒子群算法(DMPSO)在复杂问题求解时，在收敛精度和收敛成功率方面均有明显的优势.由于加强了算法的全局搜索能力，也就意味着一定程度上减弱了算法的局部搜索能力，所以在收敛速度方面则比较逊色于部分其他算法.

4 结束语

论文提出一种改进的粒子群算法，根据算法所处的迭代阶段和粒子在解空间的分布情况，动态控制惯性权重的大小；根据粒子历史最优位置的更新情况，调整粒子的飞行起点.通过4个标准测试函数的仿真试验，证明了改进后的粒子群算法在复杂问题求解时的优越性.

参考文献：

[1] KENNEDY J, EBERHART R. Particle swarm optimization[C]//IEEE Int Conference on Neural Networks Piscataway: IEEE Service Center, 1995: 1942-1948.

[2] 温涛, 盛国军, 郭权, 等. 基于改进粒子群算法的Web服务组合[J]. 计算机学报, 2013, 36 (5): 1031-1046.

[3] 梅飞, 梅军, 郑建勇, 等. 粒子群优化的KFCM及SVM诊断模型在断路器故障诊断中的应用[J]. 中国电机工程学报, 2013, 33 (36): 134-141.

[4] 陈雁, 孙海顺, 文劲宇, 等. 改进粒子群算法在船舶电力系统网络重构中的应用[J]. 电力自动化设备, 2011, 31 (3): 29-34.

[5] 高昆仑, 刘建明, 徐茹枝, 等. 基于支持向量机和粒子群的信息网络安全态势复合预测模型[J]. 电网技术, 2011, 35 (4): 176-182.

[6] 曾令全, 罗富宝, 丁金嫚. 禁忌搜索—粒子群算法在无功优化中的应用[J]. 电网技术, 2011, 35 (7): 129-133.

[7] 王庆燕, 马宏忠, 曹生让. 多策略粒子群算法在磁悬浮承重装置中的应用[J]. 中国电机工程学报, 2014, 34 (30): 5416-5424.

[8] 陈乃仕, 王海宁, 周海明, 等. 协同粒子群算法在电力市场ACE仿真中的应用[J]. 电网技术, 2010, 34 (2): 138-142.

[9] 张焱, 高兴宝. 一种改进的粒子群算法[J]. 计算机工程与应用, 2009, 45 (26): 58-59.

[10] 陈金辉, 陈辰, 董飚. 基于自适应策略的改进粒子群算法[J]. 计算机仿真, 2015, 32 (3): 298-303.

[11] 张文成, 周穗华, 吴志东, 等. 改进策略的粒子群算法及其实验测试[J]. 计算机工程与设计, 2012, 33 (10): 3945-3949.

[12] 黄太安, 生佳根, 徐红洋, 等. 一种改进的简化粒子群算法[J]. 计算机仿真, 2013: 30 (2): 327-337.

[13] SHI Y, EBERHART R. A modified particle swarm optimizer[C]//IEEE World Congress on Computational Intelligence, 1998: 69-73.

[14] 邵增珍, 王洪国, 刘弘. 具有启发式探测及自学习特征的降维对称微粒群算法[J]. 计算机科学, 2010, 37 (5): 219-222.

[15] 郭广寒, 王志刚. 一种改进的粒子群算法[J]. 哈尔滨理工大学学报, 2010, 15 (3): 31-34.

[16] 敖永才, 师奕兵, 张伟, 等. 自适应惯性权重的改进粒子群算法[J]. 电子科技大学学报, 2014, 43 (6): 874-880.