椭圆曲线y2=x(x-p)(x-q)的整数点(II)

管训贵

(泰州学院 数理学院,江苏 泰州 225300)

确定椭圆曲线的整数点是数论和算术代数几何学的有趣问题. 有关这方面的理论研究成果在现代科技中有着广泛的应用[1].其中一类典型的椭圆曲线为

y2=x(x-p)(x-q),

(1)

其中：p,q为奇素数,满足q-p=2m，m为正奇数.

对于p,q为孪生素数的情形,文[2-6]已给出一些结果. 论文对p,q的一种推广形式,证明了下面的定理.

定理设p,q为奇素数，m>1为正奇数，且q-p=2m，q≡11(mod16)，则椭圆曲线(1)除了0≤x≤q的整数点外，当m=3时，无整数点(x,y)；当m≥5时，至多有1对整数点(x,y)=(w2v2pq,±2wv(22m-6w4-v4)pq)，且w,v满足

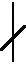
推论椭圆曲线

y2=x(x-11)(x-139)

(2)

仅有整数点(x,y)=(0,0)，(11,0)，(139,0)，(13 761,±1 605 450).

1 若干引理

引理1不定方程x2+y2=z2满足条件gcd(x,y)=1，2|x的全部正整数解可表示为

x=2ab，y=a2-b2，z=a2+b2，

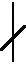
证明参见文[7].

引理2设p为奇素数，则不定方程x2+py2=z2满足条件gcd(x,y)=1的全部正整数解可表示为

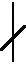
x=|a2-pb2|，y=2ab，z=a2+pb2，

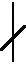
证明参见文[7].

引理3当素数p≡3(mod8)时，方程x2-2py4=1无正整数解(x,y).

证明参见文[8].

引理4设p为奇素数，则方程x4-2py2=1除了p=3有正整数解(x,y)=(7,20)外，无其他的正整数解(x,y).

证明参见文[9].

引理5当素数p≡5,7,9,11,13(mod16)时，方程

x2-8py4=1

(3)

无正整数解(x,y).

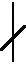
x-1=4ps4，x+1=2t4,

(4)

或

x-1=4s4，x+1=2pt4,

(5)

或

x-1=2ps4，x+1=4t4,

(6)

或

x-1=2s4，x+1=4pt4,

(7)

其中：s,t都是正整数，gcd(s,t)=1，y=st.

若(4)式成立，则得

t4-2ps4=1.

(8)

根据引理4，知(8)式无正整数解，从而(4)式不成立.

若(5)式成立，则得pt4-2s4=1，于是p≡1,3(mod16)，与已知矛盾，故(5) 式不成立.

若(6)式成立，则得2t4-ps4=1，于是p≡1,15(mod16)，与已知矛盾，故(6) 式不成立.

若(7)式成立，则得2pt4-s4=1，于是p≡1(mod8)，与已知矛盾，故(7) 式不成立.

引理5得证.

引理6设p,q为奇素数，m>1为正奇数，且q-p=2m，q≡11(mod16)，则Pell方程组

(9)

无正整数解(x,y,z).

证明由(9)式可知

y2+pz2=x2,

(10)

且gcd(y,z)=1.根据引理2，可得

(11)

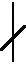
y=|a2-pb2|，z=2ab，x=a2+pb2，

(12)

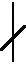
若(11)式成立，则将(11)式的后两式代入(9)式的第一式得

(13)

当m≡1(mod4)时，由引理3，知方程(13)无正整数解；当m≡3(mod4)时，由引理5知方程(13)无正整数解. 故(11)式不成立.

若(12)式成立，则将(12)式的后两式代入(9)式的第一式得

(a2-(2q-p)b2)2-2m+2qb4=1.

(14)

当m≡1(mod4)时，由引理5，知方程(14)无正整数解；当m≡3(mod4)时，由引理3知方程(14)无正整数解. 故(14)式不成立.

引理6得证.

引理7设a,b是非平方的正整数,gcd(a,b)=1，则不定方程

aX2-bY4=1，

当a>1时,至多有1组正整数解(X,Y)；当a=1时,至多有2组正整数解(X,Y).

证明参见文[10].

2 定理的证明

显然,当y=0时，(1)仅有整数点(x,y)=(0,0)，(p,0)，(q,0).设(x,y)是(1)的一组适合y≠0的整数点.因y2>0，故由(1)式得0q.如果0q，令d1=gcd(x,x-p)，d2=gcd(x,x-q)，d3=gcd(x-p,x-q)，有

(15)

设a,b,c∈N*且两两互素，根据(15)式，只需讨论下列8种情形.

情形1(d1,d2,d3)=(1,1,1).

此时，由(1)式得

x=a2，x-p=b2，x-q=c2，y=±abc.

(16)

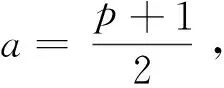
情形2(d1,d2,d3)=(1,1,2s)(1≤s≤m).

此时，由(1)式得

x=a2，x-p=2sb2，x-q=2sc2，y=±2sabc.

(17)

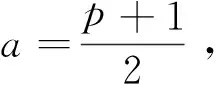
将(17)式的第二式代入第三式得

b2-c2=2m-s.

(18)

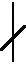
b=u2+v2，c=u2-v2， 2t=2uv，

(19)

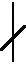
由(19)式的第三式得u=2t-1，v=1，故b=22t-2+1=2m-s-2+1，c=22t-2-1=2m-s-2-1. 知p满足

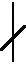
(20)

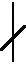
情形3(d1,d2,d3)=(1,q,1).

此时，由(1)式得

x=qa2，x-p=b2，x-q=qc2，y=±qabc.

(21)

将(21)式的第一式代入第三式得a2-c2=1，不可能.

情形4(d1,d2,d3)=(1,q,2s)(1≤s≤m).

此时，由(1)式得

x=qa2，x-p=2sb2，x-q=2s·qc2，y=±2s·qabc.

因此,有

b2-qc2=2m-s，a2-2sc2=1.

(22)

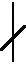
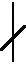
当m-s=0时，(22)式成为

b2-qc2=1，a2-2mc2=1.

(23)

由引理6,知(23)式无正整数解(a,b,c).此时，椭圆曲线(1)无整数点.

当m-s=2，即m≥3时，由(22)式的第一式,知b2-qc2=4，故b,c同奇同偶，但gcd(b,c)=1，所以b,c均为奇数，对此式模8得1-q≡4(mod8)，即q≡5(mod8)，与q≡11(mod16)矛盾.

当m-s≥4，即m≥5时，由(22)式的第一式得

(24)

根据引理2及(24)式,有

(25)

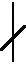
由(25)式的第一式,得

(26)

对(26)式模8得±(1-q)≡0(mod8)，即q≡1(mod8)，与q≡11(mod16)矛盾.

情形5(d1,d2,d3)=(p,1,1).

此时，由(1)式得

x=pa2，x-p=pb2，x-q=c2，y=±pabc.

(27)

将(27)式的第一式代入第二式得a2-b2=1，不可能.

情形6(d1,d2,d3)=(p,1,2s)(1≤s≤m).

此时，由(1)式,得

x=pa2，x-p=p·2sb2，x-q=2sc2，y=±2spabc.

因此,有

pb2-c2=2m-s，a2-2sb2=1.

(28)

当m-s=2时，(28)式的第一式成为pb2-c2=4，由gcd(b,c)=1,知b,c同奇，对此式模8可得p-1≡4(mod8)，即p≡5(mod8)，也与p≡3(mod8)矛盾.

当m-s≥4时，对(28)式的第一式模8,知p≡1(mod8)，仍与p≡3(mod8)矛盾.

情形7(d1,d2,d3)=(p,q,1).

此时，由(1)式,得

x=pqa2，x-p=pb2，x-q=qc2，y=±pqabc.

(29)

将(29)式的第一式代入第三式得pa2-1=c2，模p知

c2≡-1(modp)，

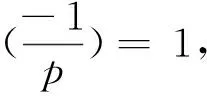
情形8(d1,d2,d3)=(p,q,2s)(1≤s≤m).

此时，由(1)式得

x=pqa2，x-p=2s·pb2，x-q=2s·qc2，y=±2s·pqabc.

因此，有

qa2-1=2sb2，pa2-1=2sc2.

(30)

若2≤s≤m，则对(30)式的第二式模4得p≡1(mod4)，与p≡3(mod8)矛盾.

若s=1，则(30)式成为

qa2-1=2b2，pa2-1=2c2.

(31)

将(31)式的两式相减得2ma2=2b2-2c2，即

(32)

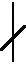
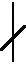
(33)

考虑到m≥3，根据引理1，由(33)式，得

(34)

其中：u,v都是正整数，且

将(31)式的第二式乘上2m-1，并将(34)式的第二式代入得

4u2v2p-2m-1=2m(u2-v2)2，

即

u2v2p=2m-3(2(u2-v2)2+1).

(35)

因2|uv，gcd(u,v)=1，故m=3时，(35)式不成立.于是m≥5.

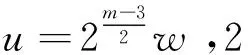
w2v2p=2(2m-3w2-v2)2+1.

(36)

2v4-(p+2m-1)w2v2+22m-5w4=-1，

(37)

又由(37)式可得

w2|(2v4+1).

令2v4+1=kw2(k为某正整数)，则

kw2-2v4=1.

(38)

由于方程w2-2v4=1没有正整数解，故k>1.根据引理7，方程(38)至多有1组正整数解(w,v)，从而方程(37) 至多有1组正整数解(v,w).

将(37)式乘上8，配方得

(4v2-(p+2m-1)w2)2-pqw4=-8，

(39)

于是方程(39)至多有1组正整数解(v,w)， 此时，椭圆曲线(1)至多有1对整数点

(x,y)=(w2v2pq,±2wv(22m-6w4-v4)pq)，

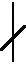
定理得证.

3 推论的证明

当y=0时，(2)式仅有整数点(x,y)=(0,0)，(11,0)，(139,0).当y≠0时，因y2>0，故由(2)式得0139.易验证：如果0139，由(p,q)=(11,139)知，(39)式成为

(4v2-75w2)2-1 529w4=-8.

(40)

因方程(40)有唯一的正整数解(v,w)=(3,1)，故此时(2)式仅有整数点(x,y)=(13 761,±1 605 450).推论得证.

参考文献：

[1] SILVERMAN J H. The arithmetic of elliptic curves[M]. New York: Springer Verlag， 1999.

[2] QIU D R， ZHANG X K. Elliptic curves of twin primes over Gauss field and Diophantine equations[J]. Advances in Mathematics China， 2000， 29 (3): 279-281.

[3] QIU D R， ZHANG X K. Mordell-Weil groups and Selmer groups of twin prime elliptic curves[J]. Science in China Series A， 2002， 45 (11): 1372-1380.

[4] LIU Z W， TANG G W， GU Y. The integral points on twin primes elliptic curve[J]. Journal of Mathematics， 2010， 30 (6): 991-1000.

[5] 陈候炎. 孪生素数椭圆曲线在p=5时的整数点[J]. 西南师范大学学报 (自然科学版)， 2011， 36 (1): 34-38.

[6] 管训贵. 关于椭圆曲线y2=x(x-p) (x-q)的整数点[J]. 北京教育学院学报 (自然科学版)， 2011， 6 (4): 7-10.

[7] 管训贵. 初等数论[M]. 2版. 合肥： 中国科学技术大学出版社， 2016.

[8] 柯召, 孙琦. 关于丢番图方程x2-Dy4=1[J]. 数学年刊， 1981， 2 (4): 491-495.

[9] 柯召, 孙琦. 关于丢番图方程x4-2py2=1的初等解法[J]. 四川大学学报 (自然科学版)， 1983 (2)： 1-3.

[10] LJUNGGREN W. Ein Satz über die diophantische GleichungAx2-By4=C(C=1， 2， 4)[J]. Skand Mat-Kongr， Lund, 1953 (54): 188-194.