A survey on analysis and synthesis of delayed Markovian jump systems
2018-03-30ZHANGBaoyongXIAWeifengLIYongmin
ZHANG Baoyong, XIA Weifeng, LI Yongmin
(1. School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China;2. School of Science, Huzhou Teachers College, Huzhou 313000, China)
0 Introduction
In a great many of practical systems, such as mechanical systems, electric power systems, flight control systems and networked control systems, there may exist sudden environment changes, random failures and repairs[1-2]. These phenomena make the system structures or parameters changing randomly. Thus, the systems can be modeled as randomly switched systems, where the switching law is described by a finite Markov chain. In references, this class of systems is referred to systems with Markovian/random switching, systems with Markovian jumping parameters (MJPs) and Markovian jump systems (MJSs). Over the past 50 years, the MJSs have been extensively studied and numerous results have been reported. The readers are referred to Refs.[1-8] for fundamental theory and recent developments on MJSs.
On the other hand, time delays are unavoidable when designing control systems. More importantly, time delays are always the cause of instability and poor performance of control systems. For these reasons, time-delay systems have received considerable attention; see, Refs.[9-14] and the references therein. The study of delayed MJSs started in the middle of 1990s and has made a great progress in the past 20 years.
The pioneer research on linear delayed MJSs was carried out in the late five years of 1990s by Benjelloun and Boukas, who investigated a series of problems on stochastic stability, robust stabilization andH∞controller design[15-19]. Almost at the same time, Shaikhet studied the asymptotic mean-square stability for a class of stochastic hereditary systems with MJPs and constant delays[20]. In 1999, Cao and Lam addressed the discrete-time MJSs with delays[21]. In 2000, Mao and his collaborators introduced a class of stochastic differential delay equations (SDDEs) with MJPs[22]. Since then, Mao has devoted his research efforts greatly to the analysis of nonlinear delayed MJSs described by SDDEs[2, 23-28]. In 2003, the neutral stochastic differential delay equations with MJPs were introduced by Kolmanovskii[29], which can be regarded as a general expression of the delayed MJSs. The stability of delayed neural networks with MJPs was primarily studied in Refs.[30-31]. In 2005, the study of delayed normal MJSs was extended to the case of singular systems[32-33].
Up to date, the study of delayed MJSs has become an important and hot research branch in the control and system area. A great number of results and methods have been developed in the literature. As more and more researchers, especially PhD and master students, are choosing the delayed MJSs as their research topics, it is necessary to provide a survey on the analysis and synthesis of delayed MJSs. However, it is impossible to include all the results on delayed MJSs in a single paper. Thus, the emphasis of this paper will be given on the study of stability analysis, feedback stabilization, and control and filtering with disturbance attenuation performances for continuous-time time-delay systems with MJPs. It is worth mentioning that the notations in the mathematical expressions in the context of this paper can be found in every paper related to the delayed MJSs, and thus their explanations are omitted in this paper.
1 Stability
Stability is the prerequisite for designing automatic control systems. Thus, the stability analysis is a fundamental problem in the study of delayed MJSs. In the literature, there are a few of different descriptions of stability concepts for delayed MJSs, among which the stochastic stability[15-18], asymptotic mean-square stability[19-20]and exponential mean-square stability[34-35]have been largely used. It is now known that the Lyapunov-Krasovskii (L-K) functional approach is a powerful tool for analyzing the stability of delayed MJSs. Therefore, in the following we briefly introduce the L-K functional approach.
1.1 Mode-dependent L-K functional approach
In general, the L-K functional approach to stability analysis of delayed MJSs contains two steps. The first step is to construct an appropriate L-K functionalV(xt,rt,t). It should be pointed out that the functional must be dependent on the system modert, otherwise there is no difference between the stability analysis of the delayed MJSs and that of deterministic time-delay systems. Therefore, the mode-dependence is the main characteristic of the L-K functional approach for delayed MJSs. The second step of the approach is to compute the weak infinitesimal generator ofV(xt,rt,t) whenrt=i, which is defined by[2,16,34]
(1)
If we can find conditions that ensure the negative definiteness of the generator defined in (1), then the stability defined in the stochastic and mean-square manner could be guaranteed.
The structure of the mode-dependent L-K functional plays a key role in the conservatism reduction of stability conditions for delayed MJSs. For ease of understanding, it is better for us to start from a simple but important class of retarded-type linear systems, which are described by
(2)
whereτ>0 denotes the time delay that can be either constant or time-varying; the modertis a right-continuous Markov chain on a probability space taking values in a finite state spaceS={1,2,…,s}. The definition of transition probability of the modes can be found in every reference related to delayed MJSs, and thus it is omitted here.
For system (2), the simplest mode-dependent L-K functional is of the following form[15-18, 36]
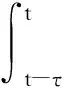
(3)
whereP(rt) andQare positive-definite matrices. This functional can lead to delay-independent stability conditions, which are quite conservative, especially when the delay is small. In order to reduce the conservatism, it is generally necessary to develop delay-dependent stability conditions. In general, the L-K functional used for developing delay-dependent stability conditions consists of three parts: non-integral terms, single-integral terms and double-integral terms. For system (2), an efficient L-K functional is of the following form[37]
(4)
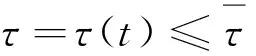
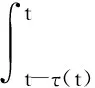
(5)
In this functional, not only the non-integral term but also the single-integral term are dependent on the system mode. If the last double integral term in (5) is further required to be dependent on the system mode, the following L-K functional is utilizable[39-42]
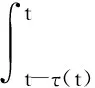
(6)
Clearly, this functional is strongly dependent on the system mode, and thus it has particular efficiency for reducing the conservatism of delay-dependent stability conditions. The advantage of functional (6) in the stability and performance analysis of linear delayed MJSs has been discussed in Refs.[40-42].
In the above, we provide a general idea to construct strongly mode-dependent L-K functionals for system (2). This idea has not been fully applied in the study of complicated MJSs, and thus the idea is expected to get more applications in the future. Next, in the context of L-K functional approach, we will briefly review the recent studies on the stability analysis problem for different kinds of delayed MJSs.
1.2 Stability analysis of linear time-delay systems with MJPs
The delay-independent stability problem for linear time-delay systems with MJPs was primarily studied in Refs.[15-17] based on the L-K functional in (3). The conditions obtained in Refs.[15-17] are expressed in terms of algebraic matrix equations. The functional (3) was also employed in Refs.[18, 36] to derive LMI-based stability conditions. In Ref.[43], the delay-dependent stability analysis for system (2) was firstly studied based on an L-K functional containing one mode-dependent non-integral term and two mode-independent double integrals. Another version of delay-dependent conditions for system (2) was obtained in Ref.[44], where the Newton-Leibniz formula was applied. In Refs.[37, 45-48], the free-weighting matrix method was applied to derive less conservative stability conditions. Some of these results were further improved in Refs.[38, 49-50] by using the L-K functionals similar to (5). Delay-dependent stability conditions based on the L-K functional (6) were given in Refs.[39-42]. Delay-partitioning techniques were applied in Refs.[51-54] to analyze the stability of system (2).
A system is called to be neutral if the differential of the system state involves delays. The stability problem for neutral systems with MJPs has been also studied. For example, the stochastic stability analysis for linear neutral MJSs with multiple constant delays was tackled in Ref.[55], where delay-independent conditions were presented. Different versions of delay-dependent stability conditions for linear neutral MJSs with time-varying delays were obtained in Refs.[56-59]. When the transition probability is partially unknown, the stability of neutral MJSs has been analyzed in Refs.[60-61].
1.3 Stability analysis of stochastic time-delay systems with MJPs
In many of works on delayed MJSs, the Brownian motions are involved in the system model. Such systems are called stochastic time-delay systems with MJPs, which are described by It-type delay differential equations. The fundamental theory of general stochastic time-delay systems with MJPs can be found in Mao’s book[2] and the recent journal papers[23-28]. The exponential mean-square stability for linear stochastic systems with MJPs, constant delays and interval uncertainties was studied in Ref.[34], where a rigorous discussion on the L-K functional with mode-dependent integrals was provided. The delay-dependent conditions for robust stability of stochastic time-delay systems with MJPs and norm-bounded uncertainties were developed in Refs.[62-63]. In Refs.[64-65], the nonlinear uncertainties were taken into account in the stochastic delayed MJSs and delay-dependent conditions of exponential mean-square stability were obtained. The neutral-type stochastic systems with MJPs were investigated in Refs.[66-68], where delay-dependent stability conditions were obtained by using different techniques.
1.4 Stability analysis of delayed neural networks with MJPs
In recent years, the artificial neural networks with time delays and MJPs have been largely studied. It is known that the artificial neural networks are described in mathematics as nonlinear systems with the nonlinear terms satisfying certain bounding conditions. By making the use of the bounding conditions in the stability analysis procedure, LMI-based conditions can be always obtained. For this reason, most of the techniques in the stability study of linear time-delay systems with or without MJPs have been generalized to delay neural networks with MJPs.
For recurrent neural networks with MJPs and time delays, the delay-independent stability conditions were obtained in Refs.[31, 69], while the delay-dependent stability conditions were presented in Refs.[70-75]. The delay-dependent stability problem for delayed Cohen-Grossberg neural networks with MJPs was investigated in Refs.[76-78]. The stochastic stability problem for delayed BAM neural networks with MJPs was considered in Refs.[79-81]. The Markovian genetic regulatory networks were studied in Refs.[82-84]. Delay-dependent stability results for neutral-type neural networks with MJPs have been also reported; see, for example, Refs.[85-88] and the references therein.
2 Stabilization
In general, the stabilization problem is formulated as designing feedback controllers such that the resulting closed-loop system is stable. When the system states are fully available, the state-feedback controllers are desirable. Otherwise, if the system states are not fully available, then the output-feedback controllers need to be designed by using measured output of the original system. It should be pointed out that, for delayed MJSs, particular attention has been paid to the design of mode-dependent controllers. In the following, we are going to survey some recent studies on the stabilization problem for different delayed MJSs.
The robust stabilization problem for linear MJSs with constant delays was addressed in the pioneer works [15-16], where two kinds of state-feedback controllers, namely linear-type controller and saturation-type controller, were designed. It is noted that the controllers in Refs.[15-16] were designed based on a constructive method. The exponential stabilization using state-feedback controllers for linear MJSs with constant delays was investigated in Refs.[47, 54, 89], where delay-dependent conditions were obtained in terms of LMIs. It is worth mentioning that the conditions obtained in Refs.[47, 54, 89] are dependent not only on the delay size but also on the decay rate of the exponential stability. When the delays depend on the system mode, the delay-independent and delay-dependent conditions for solving the state-feedback stabilization problems have been given in Refs.[50, 90-91], respectively. The memory state-feedback controller using delayed states was designed in Ref.[52] for linear delayed MJSs. When the system states are not fully available, the output-feedback stabilization problem has been considered in Refs.[45, 92-94] for different kinds of delayed MJSs. In Refs. [95-96], the finite-time stabilization problem was considered for MJSs with constant and time-varying delays, respectively. In Refs.[97-99], the stabilization of delayed MJSs was studied by using sliding-mode control approach. When the transition rates are partially unknown, the stabilization problems have been addressed in Refs.[100-102].
3 Control and filtering with disturbance attenuation performances
In this section, we are going to review the control and filtering problems for delayed MJSs with external disturbances. These problems are always formulated based on the disturbance attenuation performances such asH∞performance,L2-L∞performance, passivity and dissipativity. Hence, in the following we first give the descriptions of these performances.
3.1 Disturbance attenuation performances

An MJS is said to have anH∞performance levelγif the following inequality holds[18, 36, 38]
(7)
An MJS is said to have anL2-L∞performance levelγif the following inequality holds[110-111]
(8)
An MJS is said to be passive if the following inequality holds for all terminal timetp≥0[112]
(9)
An MJS is said to be (Q,S,R)-dissipative if the following inequality holds for some scalarα>0 and for all terminal timetp≥0[113]
(10)
whereQ,S,Rare prescribed weighting matrices.
It is easy to find that, when the weighting matricesQ,S,Rare chosen as special values, the dissipative performance defined by (10) covers the passivity andH∞performance as special cases. However, theL2-L∞performance cannot be covered by the dissipativity. Regarding this, the so-called extended dissipativity is introduced in Ref.[42]. Specifically, an MJS is said to be extended dissipative if there exists a scalarρsuch that the following inequality holds for all terminal timetp≥0
(11)
whereΨ1≤0 is a semi-negative definite matrix,Ψ3≥0 andΦ≥0 are semi-positive definite matrices, and these matrices satisfy (‖Ψ1‖+‖Ψ2‖)‖Φ‖=0. It is worth noting that (11) reduces to (10) whenΦ=0,Ψ1=Q,Ψ2=S,Ψ3=R-αIandρ=0. The inequality (11) also reduces to (8) whenΦ=I,Ψ1=0,Ψ2=0,Ψ3=γ2Iandρ=0. Therefore, the extended dissipative performance defined by(11) is quite general since it covers the (Q,S,R)-dissipative performance and theL2-L∞performance. More discussions on the definition and efficiency of the extended dissipative performance can be found in Ref.[42].
3.2 Control with disturbance attenuation performances
For delayed MJSs with energy-bounded external disturbances, it is necessary to design state-feedback and output-feedback controllers ensuring both the stability and the disturbance attenuation performances of the resulting closed-loop systems. It seems that theH∞control problem for delayed linear MJSs was first studied independently in Refs.[18, 36, 114], where state-feedback controllers were designed based on the LMI approach. These results were then improved by using different methods; see, for example, Refs.[37-38, 44, 46, 115]. TheH∞control problem for MJSs with mode-dependent delays was studied in Refs.[116-117]. TheH∞control problem for neutral type MJSs was addressed in Refs.[55-56, 107]. TheH∞control problem for stochastic time-delay systems with MJPs was investigated in Refs.[105, 118-119].
TheL2-L∞control problem for stochastic systems with time delays and MJPs was studied in Ref.[120]. By taking the passivity into account for time-delay systems with MJPs, the state-feedback controller design problem was considered in Refs.[121-122], while the output-feedback controllers were designed in Refs.[123-124]. It is also noted that the dissipative control problems for delayed MJSs have been addressed in Refs.[125-126].
3.3 Filtering with disturbance attenuation performances
TheH∞filtering problem has been extensively studied for delayed MJSs. For example, TheH∞filtering problem for MJSs with time-varying delays was investigated in Refs.[38, 41, 127-129]. For MJSs with mode-dependent delays, theH∞filtering problem was studied in Refs.[35, 130]. In context of stochastic time-delay systems with MJPs, theH∞filtering problems were studied in Refs.[131-136]. It should be noted that reduced-orderH∞filters for delayed MJSs were designed in Refs.[137-138].
TheL2-L∞filtering problems for retarded and neutral MJSs with time-varying delays were investigated in Refs.[111,139], respectively, where the transition probabilities are assumed to be partially unknown. The exponentialL2-L∞filtering for linear MJSs with distributed delays was studied in Ref.[140] by applying the delay partitioning techniques. The decentralizedL2-L∞filtering problem for a class of interconnected MJSs with constant delays was addressed in Ref.[141]. The exponentialL2-L∞filtering problem for stochastic MJSs with mixed mode-dependent delays was considered in Ref.[142]. For delayed MJSs with nonlinear uncertainties, theL2-L∞filtering problem was studied in Ref.[143].
In Ref.[42], the filter design problem for linear MJSs with time-varying delays was studied by considering the extended dissipative performance defined by (11). In that work, both mode-dependent and mode-independent filters were designed, and the delay-dependent conditions were given in terms of LMIs. It is noted that the results obtained in Ref.[42] are valid for designingH∞filters,L2-L∞filers, passivity-based filters and dissipative filters, respectively. Therefore, the Ref.[42] provides a unified framework for designing filters with different disturbance attenuation performances. The method developed in Ref.[42] is not limited to the filtering problem of delayed MJSs. Actually, the method has been applied in a number of works on different kinds of systems; see, for example, Refs.[144-148].
4 Conclusions
This paper has surveyed the studies of time-delay systems with MJPs. Since there are many subjects in the research of delayed MJSs, we cannot cover all of them. Thus, our emphasis has been mainly given on the problems of stability analysis, feedback stabilization, robust control and filtering for continuous-time systems. The study of discrete-time systems is not included in this paper. In addition, for delayed neural networks with MJPs, the stability analysis has been reviewed briefly, but the estimation and synchronization problems have not been mentioned, which have also received lots of attention recently. Therefore, this paper only includes a very small amount of references on the delayed MJSs. The readers are encouraged to pay attention to the follow-up researches based on the references provided in this paper.
Although the delay-dependent stability of delayed MJSs has been extensively studied, the results reported in the literature are still conservative to some extent, because they are only sufficient but not necessary. It is of interest to further reduce the conservatism of the stability results. For this purpose, the relaxed L-K functional approach[149-150]and complicated integral inequality techniques[151-153]may be applicable. It is also important research topics that apply the stability conditions derived by using recently developed techniques to control and filtering synthesis.
Recently, a particular attention has been paid to the semi-Markov jump systems and hidden Markov jump systems; see, for example, Refs.[154-157] and the references therein. In semi-Markov jump systems, the transition rates (or probabilities) are no longer constant, because at each time they involve the past information of elapsed jumping sequences[154-155]. In the design of hidden Markov jump systems, the modes of the original system are not available for controllers. In this case, an estimator (called detector in Refs.[156-157]) needs to be introduced to estimate the system mode. Therefore, the mode estimator and feedback controllers should be designed simultaneously for hidden Markov jump systems. It is obvious that the semi and hidden Markov jump systems generalize the traditional MJSs. However, when time delays are taken into account in the two kinds of generalized systems, the control and filtering problems have not been fully investigated, which is an interesting research topic in the future.
[1] MARITON M. Jump linear systems in automatic control[M]. New York: Marcel Dekker,1990.
[2] MAO X, YUAN C. Stochastic differential equations with Markovian switching[M]. London: Imperial College Press,2006.
[3] BOUKAS E K. Control of singular systems with random abrupt changes[M]. Berlin: Springer,2008.
[4] COSTA O L V, FRAGOSO M D, TODOROV M G. Continuous-time Markovian jump linear systems[M]. Berlin: Springer,2013.
[5] ZHANG L, YANG T, SHI P, et al. Analysis and design of Markov jump systems with complex transition probabilities[M]. Switzerland: Springer,2016.
[6] MAHMOUDM S, SHI P. Methodologies for control of jump time-delay systems[M]. Boston: Kluwer Academic Publishers,2003.
[7] HE S, SHEN H. Finite short time control and synthesis for stochastic Marov jump systems[M]. Beijing: Science Press,2018(in Chinese).
[8] SHI P, LI F. A survey on Markovian jump systems: modeling and design[J]. International Journal of Control, Automation, and Systems,2015,13(1):1-16.
[9] GU K, KHARITONOV V L, CHEN J. Stability of time-delay systems[M]. Boston: Birkhauser,2003.
[10] KHARITONOV V L. Time-delay systems[M]. New York: Springer,2013.
[11] FRIDMAN E. Introduction to time-delay systems: analysis and control[M]. Switzerland: Springer,2014.
[12] WU M, HE Y, SHE J H. Stability analysis and robust control of time-delay systems[M]. New York: Springer,2010(in Chinese).
[13] RICHARD J P. Time-delay systems: an overview of some recent advances and open problems[J]. Automatica,2003,39:1667-1694.
[14] XU S, LAM J. A survey of linear matrix inequality techniques in stability analysis of delay systems[J]. International Journal of Systems Science,2008,39(12):1095-1113.
[15] BENJELLOUN K, BOUKAS E K, YANG H. Robust stabilizability of uncertain linear time delay systems with Markovian jumping parameters[C]//Proceedings of the American Control Conference, Washington,1995:330-334.
[16] BENJELLOUN K, BOUKAS E K, YANG H. Robust stabilizability of uncertain linear time-delay systems with Markovian jumping parameters[J]. Journal of Dynamic Systems, Measurement, and Control,1996,118:776-783.
[17] BENJELLOUN K, BOUKAS E K. Stochastic stability of linear time-delay system with Markovian jumping parameters[J]. Mathematical Problems in Engineering,1997,3:187-201.
[18] BENJELLOUN K, BOUKAS EK, COSTA L V.H∞control for linear time-delay systems with Markovian jumping parameters[J]. Journal of Optimization Theory and Applications,2000,105(1):73-95.
[19] BENJELLOUN K, BOUKAS E K. Mean square stochastic stability of linear time-delay system with Markovian jumping parameters[J]. IEEE Transactions on Automatic Control,1998,43(10):1456-1460.
[20] SHAIKHET L. Stability of stochastic hereditary systems with Markov switching[J]. Theory of Stochastic Processes,1996,2(18):180-184.
[21] CAO Y Y, LAM J. Stochastic stabilizability andH∞control for discrete-time jump linear systems with time delay[J]. Journal of the Franklin Institute,1999,336:1263-1281.
[22] MAO X, MATASOV A, PIUNOVSKIY A B. Stochastic differential delay equations with Markovian switching[J]. Bernoulli,2000,6(1):73-90.
[23] MAO X. Robustness of stability of stochastic differential delay equations with Markovian switching[J]. Stability and Control: Theory and Applications,2000,3(1):48-61.
[24] MAO X, SHAIKHET L. Delay-dependent stability criteria for stochastic differential delay equations with Markovian switching[J]. Stability and Control: Theory and Applications,2000,3(2):87-101.
[25] YUAN C, ZOU J, MAO X. Stability in distribution of stochastic differential delay equations with Markovian switching[J]. Systems & Control Letters,2003,50:195-207.
[26] YUAN C, MAO X. Robust stability and controllability of stochastic differential delay equations with Markovian switching[J]. Automatica,2004,40:343-354.
[27] HUANG L, MAO X. On input-to-state stability of stochastic retarded systems with Markovian switching[J]. IEEE Transactions on Automatic Control,2009,54(8):1898-1902.
[28] FENG L, LI S, MAO X. Asymptotic stability and boundedness of stochastic functional differential equations with Markovian switching[J]. Journal of the Franklin Institute,2016,353(18):4924-4949.
[29] KOLMANOVSKII V, KOROLEVA N, MAIZENBERG T, et al. Neutral stochastic differential delay equations with Markovian switching[J]. Stochastic Analysis and Applications,2003,21(4):839-867.
[30] XIE L. Stochastic robust stability analysis for discrete-time neural networks with Markovian jumping parameters and time delays[C]//Proceedings of the30th Annual Conference of the IEEE Industrial Electronics Society, Korea,2004:1743-1748.
[31] XIE L. Stochastic robust stability analysis for Markovian jumping neural networks with time delays[C]// Proceedings of2005Conference on Networking, Sensing and Control, Tucson, USA,2005:923-928.
[32] BOUKAS E K, XU S, LAM J. On stability and stabilizability of singular stochastic systems with delays[J]. Journal of Optimization Theory and Applications,2005,127(2):249-262.
[33] FU Y M, DUAN G R. Robust guaranteed cost observer for uncertain descriptor time-delay systems with Markovian jumping parameters[J]. Acta Automatica Sinica,2005,31(3):479-483.
[34] MAO X. Exponential stability of stochastic delay interval systems with Markovian switching[J]. IEEE Transactions on Automatic Control,2002,47(10):1604-1612.
[35] XU S, CHEN T, LAM J. RobustH∞filtering for uncertain Markovian jump systems with mode-dependent time delays[J]. IEEE Transactions on Automatic Control,2003,48(5):900-907.
[36] CAO Y Y, LAM J. RobustH∞control of uncertain Markovian jump systems with time-delay[J]. IEEE Transactions on Automatic Control,2000,45(1):77-83.
[37] CAO Y Y, YAN W, XUE A. Improved delay-dependent stability conditions andH∞control for jump time-delay systems[C]//Proceedings of the43rd IEEE Conference on Decision and Control, Bahamas,2004:4527-4532.
[38] XU S, LAM J, MAO X. Delay-dependentH∞control and filtering for uncertain Markovian jump systems with time-varying delays[J]. IEEE Transactions on Circuits and Systems-I: Regular Papers,2007,54(9):2070-2077.
[39] ZHANG B, XU S, ZHANG Y, et al. Delay-dependent stabilization for delayed Markovian jump systems subject to input saturation[C]//Proceedings of the29th Chinese Control Conference, Beijing,2010:5981-5986.
[40] ZHANG B, XU S, LI Y.H∞tracking control for time-delay systems with Markovian jumping parameters[C]// Proceedings of the12th International Conference on Control, Automation, Robotics & Vision, Guangzhou,2012:1501-1506.
[41] ZHANG B, ZHENG W X, XU S. On robustH∞filtering of uncertain Markovian jump time-delay systems[J]. International Journal of Adaptive Control and Signal Processing,2012,26:138-157.
[42] ZHANG B, ZHENG W X, XU S. Filtering of Markovian jump delay systems based on a new performance index[J]. IEEE Transactions on Circuits and Systems-I: Regular Papers,2013,60(5):1250-1263.
[43] BOUKAS E K, LIU Z K, LIU G X. Delay-dependent robust stability andH∞control of jump linear systems with time-delay[J]. International Journal of Control,2001,74(4):329-340.
[44] CAO Y Y, LAM J, HU L. Delay-dependent stochastic stability andH∞analysis for time-delay systems with Markovian jumping parameters[J]. Journal of the Franklin Institute,2003,340:423-434.
[45] CHEN W H, GUAN Z H, LU X. Delay-dependent output feedback stabilisation of Markovian jump system with time-delay[J]. IEE Control Theory and Applications,2004,151(5):561-566.
[46] WU J, CHEN T, WANG L. Delay-dependent robust stability andH∞control for jump linear systems with delays[J]. Systems & Control Letters,2006,55:939-948.
[47] SHU Z, LAM J, XU S. Robust stabilization of Markovian delay systems with delay-dependent exponential estimates[J]. Automatica,2006,42:2001-2008.
[48] HU L S, SHI P, CAO Y Y. Delay-dependent filtering design for time-delay systems with Markovian jumping parameters[J]. International Journal of Adaptive Control and Signal Processing,2007,21:434-448.
[49] ZHAO X, LING M, ZENG Q. Delay-dependent stability criterion andH∞analysis for Markovian jump systems with time-varying delays[J]. Asian Journal of Control,2011,13(2):232-239.
[50] ZHAO X, ZENG Q. Stabilization of jump linear systems with mode-dependent time-varying delays[J]. Optimal Control Applications and Methods,2011,32:139-152.
[51] ZHAO X, ZENG Q. New robust delay-dependent stability andH∞analysis for uncertain Markovian jump systems with time-varying delays[J]. Journal of the Franklin Institute,2010,347:863-874.
[52] FEI Z, GAO H, SHI P. New results on stabilization of Markovian jump systems with time delay[J]. Automatica,2009,45:2300-2306.
[53] GAO H, FEI Z, LAM J, et al. Further results on exponential estimates of Markovian jump systems with mode-dependent time-varying delays[J]. IEEE Transactions on Automatic Control,2011,56(1):223-229.
[54] HUANG H, FENG G. Exponential stabilization of uncertain time-delay linear systems with Markovian jumping parameters[J]. Asian Journal of Control,2012,14(2):527-537.
[55] ISMAIL A, MAHMOUD M S. LMI approach to robust stability andH∞control for uncertain neutral jumping systems[J]. IMA Journal of Mathematical Control and Information,2004,21:115-141.
[56] CHEN W H, GUAN Z H, LU X M. RobustH∞control of neutral delay systems with Markovian jumping parameters[J]. Journal of Control Theory and Applications,2003,20(5):776-778.
[57] HE S P, LIU F. Exponential stability for uncertain neutral systems with Markov jumps[J]. Journal of Control Theory Applications,2009,7(1):35-40.
[58] BALASUBRAMANIAM P, MANIVANNAN A, RAKKIYAPPAN R. Exponential stability results for uncertain neutral systems with interval time-varying delays and Markovian jumping parameters[J]. Applied Mathematics and Computation,2010,216(11):3396-3407.
[59] QIU J Q, CHEN J, SHI P, et al. New stochastic robust stability criteria for time-varying delay neutral systems with Markovian jump parameters[J]. International Journal of Control, Automation, and Systems,2010,8(2):418-424.
[60] XIONG L, TIAN J, LIU X. Stability analysis for neutral Markovian jump systems with partially unknown transition probabilities[J]. Journal of the Franklin Institute,2012,349:2193-2214.
[61] XIONG L, ZHANG H, LI Y, et al. Improved stability andH∞performance for neutral systems with uncertain Markovian jump[J]. Nonlinear Analysis: Hybrid Systems,2016,19:13-25.
[62] YUE D, FANG J, WON S. Delay-dependent robust stability of stochastic uncertain systems with time delay and Markovian jump parameters[J]. Circuits, Systems and Signal Processing,2003,22(4):351-365.
[63] BALASUBRAMANIAM P, KRISHNASAMY R, RAKKIYAPPAN R.Delay-interval-dependent robust stability results for uncertain stochastic systems with Markovian jumping parameters[J]. Nonlinear Analysis: Hybrid Systems,2011,5:681-691.
[64] YUE D, HAN Q L. Delay-dependent exponential stability of stochastic systems with time-varying delay, nonlinearity, and Markovian switching[J]. IEEE Transactions on Automatic Control,2005,50(2):217-222.
[65] HE Y, ZHANG Y, WU M, et al. Improved exponential stability for stochastic Markovian jump systems with nonlinearity and time-varying delay[J]. International Journal of Robust and Nonlinear Control,2010,20:16-26.
[66] XIE J, KAO Y, WANG C, et al. Delay-dependent robust stability of uncertain neutral-type Itstochastic systems with Markovian jumping parameters[J]. Applied Mathematics and Computation,2015,251:576-585.
[67] CHEN W, XU S, ZHANG B, et al. Stability and stabilization of neutral stochastic delay Markovian jump systems[J]. IET Control Theory and Applications,2016,10(15):1798-1807.
[68] CHEN W, ZHANG B, MA Q. Decay-rate-dependent conditions for exponential stability of stochastic neutral systems with Markovian jumping parameters[J]. Applied Mathematics and Computation,2018,321:93-105.
[69] WANG Z, LIU Y, YU L, et al. Exponential stability of delayed recurrent neural networks with Markovian jumping parameters[J]. Physics Letters A,2006,356(4/5):346-352.
[70] ZHU Q, CAO J. Exponential stability of stochastic neural networks with both Markovian jump parameters and mixed time delays[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part B: Cybernetics,2011,41(2):341-353.
[71] CHEN W, MA Q, MIAO G, et al. Stability analysis of stochastic neural networks with Markovian jump parameters using delay-partitioning approach[J]. Neurocomputing,2013,103:22-28.
[72] XIE J, KAO Y. Stability of Markovian jump neural networks with mode-dependent delays and generally incomplete transition probability[J]. Neural Computing and Applications,2015,26:1537-1553.
[73] ZHOU L.Delay-dependent exponential stability of recurrent neural networks with Markovian jumping parameters and proportional delays[J]. Neural Computing and Applications,2017,28:765-773.
[74] SARAVANAKUMAR R, ALI M S, AHN C K, et al. Stability of Markovian jump generalized neural networks with interval time-varying delays[J]. IEEE Transactions on Neural Networks and Learning Systems,2017,28(8):1840-1850.
[75] GRIENGGRAI R, AJCHAKIT G, SARAVANAKUMAR R. Exponential stability of semi-Markovian jump generalized neural networks with interval time-varying delays[J]. Neural Computing and Applications,2018,29(2):483-492.
[76] ZHANG H, WANG Y. Stability analysis of Markovian jumping stochastic Cohen-Grossberg neural networks with mixed time delays[J]. IEEE Transactions on Neural Networks,2008,19(2):366-370.
[77] ZHU Q, CAO J. Robust Exponential stability of Markovian jump impulsive stochastic Cohen-Grossberg neural networks with mixed time delays[J]. IEEE Transactions on Neural Networks,2010,21(8):1314-1325.
[78] LIU Y, LIU W, OBAID M A, et al. Exponential stability of Markovian jumping Cohen-Grossberg neural networks with mixed mode-dependent time-delays[J]. Neurocomputing,2016,177:409-415.
[79] LOU X, CUI B.Stochastic exponential stability for Markovian jumping BAM neural networks with time-varying delays[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part B: Cybernetics,2007,37(3):713-719.
[80] ZHU Q, CAO J. Stability analysis of Markovian jump stochastic BAM neural networks with impulse control and mixed time delays[J] IEEE Transactions on Neural Networks and Learning Systems,2012,23(3):467-479.
[81] ZHU Q, RAKKIYAPPAN R, CHANDRASEKAR A. Stochastic stability of Markovian jump BAM neural networks with leakage delays and impulse control[J]. Neurocomputing,2014,136:136-151.
[82] LIANG J, LAM J, WANG Z. State estimation for Markov-type genetic regulatory networks with delays and uncertain mode transition rates[J]. Physics Letters A,2009,373:4328-4337.
[83] ZHANG B, XU S, CHU Y, et al. Delay-dependent stability for Markovian genetic regulatory networks with time-varying delays[J]. Asian Journal of Control,2012,14(5):1403-1406.
[84] LIU J, TIAN E, GU Z, et al. State estimation for Markovian jumping genetic regulatory networks with random delays[J]. Communications in Nonlinear Science and Numerical Simulation,2014,19(7):2479-2492.
[85] ZHU Q, CAO J. Stability analysis for stochastic neural networks of neutral type with both Markovian jump parameters and mixed time delays[J]. Neurocomputing,2010,73:2671-2680.
[86] CHEN W, WANG L. Delay-dependent stability for neutral-type neural networks with time-varying delays and Markovian jumping parameters[J]. Neurocomputing,2013,120:569-576.
[87] XIA J, PARK J H, ZENG H. Improved delay-dependent robust stability analysis for neutral-type uncertain neural networks with Markovian jumping parameters and time-varying delays[J]. Neurocomputing,2015,149:1198-1205.
[88] ZHENG C D, LUE X, LIANG W, et al. Robust stochastic convergence and stability of neutral-type neural networks with Markovian jump and mixed delays[J].2015,29(2):158-179.
[89] HUANG H, FENG G, CHEN X. Stability and stabilization of Markovian jump systems with time delay via new Lyapunov functionals[J]. IEEE Transactions on Circuits and Systems-I: Regular Papers,2012,59(10):2413-2421.
[90] BOUKAS E K, LIU Z K. Robust stability and stabilizability of Markov jump linear uncertain systems with mode-dependent time delays[J]. Journal of Optimization Theory and Applications,2001,109(3):587-600.
[91] WANG G, ZHANG Q, SREERAM V. Robust delay-range-dependent stabilization for Markovian jump systems with mode-dependent time delays and nonlinearities[J]. Optimal Control Applications and Methods,2010,31:249-264.
[92] ZHANG Y, ZHANG Q.Delay-range-dependent robust output-feedback stabilization for Markovian jump systems with mode-dependent time delays and nonliearities[C]//Proceedings of the29th Chinese Control Conference, Beijing,2010:1983-1986.
[93] YU J, TAN J, JIANG H, et al. Dynamic output feedback control for Markovian jump systems with time-varying delays[J]. IET Control Theory and Applications,2012,6(6):803-812.
[94] CHENG J, PARK J H, KARIMI H R, et al. Static output feedback control of nonhomogeneous Markovian jump systems with asynchronous time delays[J]. Information Science,2017,399:219-238.
[95] WEN J, NGUANG S K, SHI P, et al. Finite-time stabilization of Markovian jump delay systems: a switching control approach[J]. International Journal of Robust and Nonlinear Control,2017,27(2):298-318.
[96] HE S, LIU F. Observer-based finite-time control of time-delayed jump systems[J]. Applied Mathematics and Computation,2010,217(6):2327-2338.
[97] HUANG R, LIN Y, LIN Z.Mode-independent stabilization of Markovian jump systems with time-varying delays: a sliding mode approach[J]. Journal of Dynamic Systems, Measurement, and Control,2012,134(5):051009.
[98] QI W, PARK J H, CHENG J, et al. Robust stabilization for nonlinear time-delay semi-Markovian jump systems via sliding mode control[J]. IET Control Theory and Applications,2017,11(10):1504-1513.
[99] KAO Y, XIE J, ZHANG L, et al. A sliding mode approach to robust stabilisation of Markovian jump linear time-delay systems with generally incomplete transition rates[J]. Nonlinear Analysis: Hybrid Systems,2015,17:70-80.
[100] DU B, LAM J, ZOU Y, et al. Stability and stabilization for Markovian jump time-delay systems with partially unknown transition rates[J]. IEEE Transactions on Circuits and Systems-I: Regular Papers,2013,60(2):341-351.
[101] LI Z, FEI Z, KARIMI H R. New results on stability analysis and stabilization of time-delay continuous Markovian jump systems with partially known rates matrix[J]. International Journal of Robust and Nonlinear Control,2016,26:1873-1887.
[102] LI Z, XU Y, FEI Z, et al. Stability analysis and stabilization of Markovian jump systems with time-varying delay and uncertain transition information[J]. International Journal of Robust and Nonlinear Control,2018,28(1):68-85.
[103] WANG Z, LIU Y, LIU X. Exponential stabilization of a class of stochastic system with Markovian jump parameters and mode-dependent mixed time-delays[J]. IEEE Transactions on Automatic Control,2010,55(7):1656-1662.
[104] WANG Z, QIAO H, BURNHAM K J. On stabilization of bilinear uncertain time-delay stochastic systems with Markovian jumping parameters[J]. IEEE Transactions on Automatic Control,2002,47(4):640-646.
[105] SENTHILKUMAR T, BALASUBRAMANIAM P. Delay-dependent robust stabilization andH∞control for nonlinear stochastic systems with Markovian jump parameters and interval time-varying delays[J]. Journal of Optimization Theory and Applications,2011,151(1):100-120.
[106] WANG G, LI Z, ZHANG Q, et al. Robust finite-time stability and stabilization of uncertain Markovian jump systems with time-varying delays[J]. Applied Mathematics and Computation,2017,293:377-393.
[107] CHEN W, MA Q, WANG L, et al. Stabilisation andH∞control of neutral stochastic delay Markovian jump systems[J]. International Journal of Systems Sciences,2018,49(1):58-67.
[108] MAO X, LAM J, HUANG L.Stabilisation of hybrid stochastic differential equations by delay feedback control[J]. Systems & Control Letters,2008,57:927-935.
[109] MA L, DA F P, WU L.Delayed-state-feedback exponential stabilization of stochastic Markovian jump systems with mode-dependent time-varying state delays[J]. Acta Automatica Sinica,2010,36(11):1601-1610.
[110] GAO H, LAM J, WANG C. Robust energy-to-peak filter design for stochastic time-delay systems[J]. Systems & Control Letters,2006,55(2):101-111.
[111] DING Y, ZHU H, ZHONG S, et al.L2-L∞filtering for Markovian jump systems with time-varying delays and partly unknown transition probabilities[J]. Communications in Nonlinear Science and Numerical Simulation,2012,17:3070-3081.
[112] CHEN W H, GUAN Z H, LU X, et al. Passive control synthesis for uncertain Markovian jump systems with multiple mode-dependent time-delays[J]. Asian Journal of Control,2005,7(2):135-143.
[113] FENG Z, LAM J. Reliable dissipative control for singular Markovian systems[J]. Asian Journal of Control,2013,15(4):1-10.
[114] GAO J, HUANG B, WANG Z. LMI-based on robustH∞control for uncertain linear jump systems with time-delays[J]. Automatica,2001,37:1141-1146.
[115] QIU J, WEI Y, KARIMI H R. New approach to delay-dependentH∞control for continuous-time Markovian jump systems with time-varying delay and deficient transition descriptions[J]. Journal of the Franklin Institute,2015,352:189-215.
[116] KANG Y, ZHANG J F, GE S S. Robust output feedbackH∞control of uncertain Markovian jump systems with mode-dependent time-delays[J]. International Journal of Control,2008,81(1):43-61.
[117] ZHAO H, CHEN Q, XU S.H∞guaranteed cost control for uncertain Markovian jump systems with mode-dependent distributed delays and input delays[J]. Journal of the Franklin Institute,2009,346(10):945-957.
[118] XIA J, SUN C, ZHANG B. New robustH∞control for uncertain stochastic Markovian jumping systems with mixed delays based on decoupling method[J]. Journal of the Franklin Institute,2012,349(3):741-769.
[119] SARAVANAKUMAR R, SYED A, LI M, et al. RobustH∞control of uncertain stochastic Markovian jump systems with mixed time-varying delays[J]. International Journal of Systems Science,2017,48(4):862-872.
[120] LIU H, DUAN G. Energy-to-peak control for Itstochastic differential systems with time delay and Markovian switching[C]//Proceedings of the27th Chinese Control Conference, Kunming,2008:794-797.
[121] CHEN G, GAO Y, ZHU S. Finite-time dissipative control for stochastic interval systems with time-delay and Markovian switching[J]. Applied Mathematics and Computation,2017,310:169-181.
[122] YAO X, WU L, ZHENG W X, et al. Passivity analysis and passification of Markovian jump systems[J]. Circuits, Systems and Signal Processing,2010,29(4):709-725.
[123] ZHANG B, ZHENG W, XU S. Delay-dependent passivity and passification for uncertain Markovian jump systems with time-varying delays[J]. International Journal of Robust and Nonlinear Control,2012,22(16):1837-1852.
[124] KARIMI H R. Passivity-based output feedback control of Markovian jump systems with discrete and distributed time-varying delays[J]. International Journal of Systems Science,2013,44(7):1290-1300.
[125] WANG G, ZHANG Q, YANG C. Dissipative control for singular Markovian jump systems with time delay[J]. Optimal Control Applications and Methods,2012,33(4):415-432.
[126] XIA W, LI Y, CHU Y, et al. Dissipative filter design for uncertain Markovian jump systems with mixed delays and unknown transition rates[J]. Signal Processing,2017,141:176-186.
[127] LI Z, YU Z, ZHAO H. Further result onH∞filter design for continuous-time Markovian jump systems with time-varying delay[J]. Journal of the Franklin Institute,2014,351:4619-4635.
[128] YANG H, SHI P, ZHANG J, et al. RobustH∞filtering for a class of Markovian jump systems with time-varying delays based on delta operator approach[J]. Asian Journal of Control,2011,13(3):398-407.
[129] WEI Y, QIU J, KARIMI H R, et al. A new design ofH∞filtering for continuous-time Markovian jump systems with time-varying delay and partially accessible mode information[J]. Signal Processing,2013,93:2392-2407.
[130] ZHAO H, XU S, ZOU Y. RobustH∞filtering for uncertain Markovian jump systems with mode-dependent distributed delays[J]. International Journal of Adaptive Control and Signal Processing,2010,24:83-94.
[131] SHAO H. Delay-range-dependent robustH∞filtering for uncertain stochastic systems with mode-dependent time delays and Markovian jump parameters[J]. Journal of Mathematical Analysis and Applications,2008,342:1084-1095.
[132] MA L, DA F. ExponentialH∞filter design for stochastic time-varying delay systems with Markovian jumping parameters[J]. International Journal of Robust and Nonlinear Control,2010,20:802-817.
[133] ZHUANG G, WEI Y. Non-fragileH∞filter design for uncertain stochastic nonlinear time-delay Markovian jump systems[J]. Circuits, Systems, and Signal Processing,2014,33(1):3389-3419.
[134] SHEN H, XU S, SONG X, et al. Delay-dependentH∞filtering for stochastic systems with Markovian switching and mixed mode-dependent delays[J]. Nonlinear Analysis: Hybrid Systems,2010,4:122-133.
[135] CHEN Y, ZHENG W X. ExponentialH∞filtering for stochastic Markovian jump systems with time delays[J]. International Journal of Robust and Nonlinear Control,2014,24(4):625-643.
[136] HUA M, TAN H, CHEN J, et al. Robust delay-range-dependent non-fragileH∞filtering for uncertain neutral stochastic systems with Markovian switching and mode-dependent time delays[J]. Journal of the Franklin Institute,2015,352:1318-1341.
[137] LIU H, SUN F, HE K, et al. Design of reduced-orderH∞filter for Markovian jumping systems with time delay[J]. IEEE Transactions on Circuits and Systems-II: Express Briefs,2004,51(11):607-612.
[138] WANG G, ZHANG Q, SREERAM V.2009Design of reduced-orderH∞filtering for Markovian jump systems with mode-dependent time delays[J]. Signal Processing,2009,89:187-196.
[139] BALASUBRAMANIAM P, REVATHI V M, PARK J H.L2-L∞filtering for neutral Markovian switching system with mode-dependent time-varying delays and partially unknown transition probabilities[J]. Applied Mathematics and Computation,2013,219:9524-9542.
[140] ZHANG B, LI Y. ExponentialL2-L∞filtering for distributed delay systems with Markovian jumping parameters[J]. Signal Processing,2013,93:206-216.
[141] LI Y, FEI S, ZHANG B, et al. DecentralizedL2-L∞filtering for interconnected Markovian jump systems with delays[J]. Circuits Systems and Signal Processing,2012,31:889-909.
[142] CHEN Z, HUANG Q. ExponentialL2-L∞filtering for a class of stochastic system with Markovian jump parameters and mixed mode-dependent time-delays[J]. International Journal of Control, Automation, and Systems,2014,12(3):552-563.
[143] CHEN Y, ZHENG W X.L2-L∞filtering for stochastic Markovian jump delay systems with nonlinear perturbations[J]. Signal Processing,2015,109:154-164.
[144] LEE T H, PARK M J, PARK J H, et al. Extended dissipative analysis for neural networks with time-varying delays[J]. IEEE Transactions on Neural Networks and Learning Systems,2014,25(10):1936-1941.
[145] FENG Z, ZHENG W X. On extended dissipativity of discrete-time neural networks with time delay[J]. IEEE Transactions on Neural Networks and Learning Systems,2015,26(12):3293-3300.
[146] AHN C K, SHI P. Generalized dissipativity analysis of digital filters with finite-wordlength arithmetic[J]. IEEE Transactions on Circuits and Systems II: Express Briefs,2016,63(4):386-390.
[147] ZHUANG G, XU S, ZHANG B, et al. Unified filters design for singular Markovian jump systems with time-varying delays[J]. Journal of the Franklin Institute,2016,353(15):3739-3768.
[148] SHEN H, ZHU Y, ZHANG L, et al. Extended dissipative state estimation for Markov jump neural networks with unreliable links[J]. IEEE Transactions on Neural Networks and Learning Systems,2017,28(2):346-358.
[149] XU S, LAM J, ZHANG B, et al. New insight into delay-dependent stability of time-delay systems[J]. International Journal of Robust and Nonlinear Control,2015,25(7):961-970.
[150] ZHANG B, LAM J, XU S.Stability analysis of distributed delay neural networks based on relaxed Lyapunov-Krasovskii functionals[J]. IEEE Transactions on Neural Networks and Learning Systems,2015,26(7):1480-1492.
[151] CHEN J, XU S, ZHANG B. Single/multiple integral inequalities with applications to stability analysis of time-delay systems[J]. IEEE Transactions on Automatic Control,2017,62(7):3488-3493.
[152] LIU K, SEURET A, XIA Y. Stability analysis of systems with time-varying delays via the second-order Bessel-Legendre inequality[J]. Automatica,2017,76:138-142.
[153] SEURET A, GOUAISBAUT F. Stability of linear systems with time-varying delays using Bessel-Legendre inequalities[J]. IEEE Transactions on Automatic Control,2018,63(1):225-232.
[154] LI F, SHI P, WU L. Control and filtering for semi-Markovian jump systems[M]. Berlin: Springer,2017.
[155] ZHANG L, YANG T, COLANERI P. Stability and stabilization of semi-Markov jump linear systems with exponentially modulated periodic distributions of sojourn time[J]. IEEE Transactions on Automatic Control,2017,62(6):2870-2875.
[156] STADTMANN F, COSTA L V.H2-control of continuous-time hidden Markov jump linear systems[J]. IEEE Transactions on Automatic Control,2017,62(8):4031-4037.
[157] DE OLIVEIRA A M, COSTA L V. MixedH2/H∞control of hidden Markov jump systems[J]. International Journal of Robust and Nonlinear Control,2018,28(4):1261-1280.
