随机多模态系统的有限频段性能研究综述

栾小丽，万海英，刘 飞

(江南大学 自动化研究所 轻工过程先进控制教育部重点实验室，江苏 无锡 214122)

工程领域中存在既随时间演化又被事件驱动的混杂多模态系统，如生化反应系统、流程制造系统、网络通信系统及经济系统等[1-5].此类系统运行过程中时常受到外部环境突变、内部元件参数变化及人为干预等的影响，导致系统呈现强时变、非线性的特征.鉴于此，多模态混杂系统能更好描述实际工业过程中的复杂对象.切换系统[6-8]和Markov跳变系统[9-11]是两种典型的混杂系统.这两类系统的区别为：Markov跳变系统每一时刻所处的模态是随机的，且子模态间的转换规律符合Markov过程，而切换系统模态间的切换规则是确定的.虽然某种程度上，混杂系统可视为单模态系统的推广，但对此类结构异常复杂、含有多模态子系统的动态系统，经典的线性系统理论已不能完整刻画其动态行为，一般的线性系统研究成果也不能直接应用于它.因此，多模态混杂系统不仅在理论研究中有重要作用，而且在工程领域有广泛的应用价值.

一般来说，系统的性能研究可从时域、频域两个角度出发，二者表征系统两个不同维度上的信息.时域主要研究系统随时间变化的动态及稳态性能，通过设计控制器、滤波器等，使系统满足实际工程所需的性能指标要求，如系统稳定性、鲁棒性等；频域则是通过使闭环系统的频率响应特性(如幅频特性、极点分布等)满足一定要求，来保证被控系统具有相应的性能指标[12].在现有频域研究成果中，多数成果基于全频段，鲜有涉及有限频段的控制问题.然而，实际工程中许多信号，除了白噪声均匀分布于全频段外，无论是系统扰动[13-14]还是参考输入信号[15-16]，其能量往往只集中在某些频段内，如地震波信号的能量大部分集中在0.3～8Hz频段[17]，高速列车引起的地基振动的频率主要集中在0～100Hz[18]，人体对外力较为敏感的频段为4～8Hz[19-20]等.因此，控制系统设计中，若能基于信号及系统的有限频域特性设计控制器，系统将会获得更好的性能.另一方面，由于不同频段影响系统性能的主导因素不同，为优化系统性能，则要求不同频率范围内满足不同性能指标，如对数字滤波器而言，低频段需要控制器具有高增益以确保系统有较强抗干扰能力，而高频段则需低增益以减小模型不确定性对系统性能的影响[21].这就意味着对系统进行分析及综合时，应充分考虑其频率特性.综上所述，对更加贴近实际工程的多模态混杂系统而言，研究其有限频段性能不仅能完善理论体系，也能解决工程应用问题.该文梳理有限频段性能研究的进程，分析多模态系统有限频段性能研究的现状，讨论该领域有待深入研究的几个问题.

1 主要研究方法

1.1 经典控制方法

基于经典控制理论的频域分析方法，通过控制器引入附加零极点，使被控系统具有期望的频率响应特性，而此方法只适用于单输入单输出的线性定常系统，对于多输入多输出、高阶等复杂系统无法处理.另外，经典控制理论中的频域分析方法一般是利用频率特性曲线来分析系统时域的瞬态及稳态性能，此方法并没有将有限频段信息融入控制器设计，因此难以用于实际的有限频段性能研究.

1.2 频率加权法

频率加权法是基于状态空间方程的一种研究方法，它克服了经典控制方法不适用于复杂系统的不足.其原理是通过设计合适的加权传递函数，将原系统的有限频域问题转为复合系统的全频域问题，从而间接实现原系统的有限频域控制.该方法不仅能将控制理论直接用于有限频段控制，而且其加权函数能反映多维信号各分量在系统中的重要性.文献[22]针对H2和H∞混合灵敏度问题，提出了适用于平衡模型降阶的频率加权方法.随后，基于频率加权法的有限频段控制问题大量涌现，如控制器降阶问题[23]、模型降阶问题[24-26]等.然而，频率加权法也存在许多弊端：首先，难以找到合适的加权函数，寻找只能根据工程经验，过程十分复杂且费时；其次，频率加权法并没有直接给出系统有限频段性能的定量信息；最后，加权函数越复杂控制器的维数越大，使得求解困难.因此，基于频率加权法的有限频段研究进展缓慢.

1.3 GKYP引理法

General Kalman-Yakubovich-Popov(GKYP)引理法是对Kalman-Yakubovich-Popov(KYP)引理进行推广得到的一种解决有限频段问题的新方法[27-28].该方法将系统的有限频域特性直接刻画成等价的线性矩阵不等式，为控制系统有限频段性能研究提供了新思路.相比其他有限频段性能研究方法，GKYP具有以下优点：1)有严谨的数学推导过程；2)有限频段性能的基础理论完善；3)其性能具有明确的频域意义.

2 GKYP引理及其推广

2.1 GKYP引理

给出GKYP引理之前，定义有限频段如下

由于频域不等式可直接用来描述动态系统的频段特性，则上述有限频段的复频域表示可为

其中：[·]*表示矩阵的共轭转置；Φ,Ψ∈H2(Hn为n×n埃尔米特矩阵)，且det(Ψ)<0，矩阵Φ决定集合Λ所刻画的系统类型，矩阵Ψ表征所对应频段.特别地，当Ψ=0时，集合Λ(Φ,Ψ)所描述的是全频段.

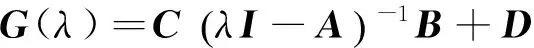
(1) 有限频段不等式

(1)

(2) 存在对称矩阵P，Q，Q>0，且

(2)

其中：Ξ=Φ⊗P+Ψ⊗Q，其表征系统的频域信息.表 1 为频域信息对照，其中ωc=(ω1+ω2)/2，ϑc=(ϑ1+ϑ2)/2，ϑd=(ϑ2-ϑ1)/2.

表1 频域信息对照

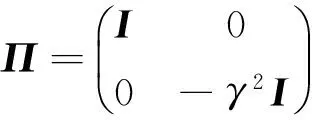
需要指出的是，GKYP引理中两个等价条件的转化是无损的，这就意味着，条件(1)的无限维验证问题可简化为求解条件(2)中线性矩阵不等式的有限维问题.该引理架起了有限频段性能与线性矩阵不等式可行解存在性间的桥梁，为解决控制系统中许多难以解决的复杂问题提供了新工具.

2.2 引理的推广

GKYP引理只适用于一般的线性系统，而实际工程中许多复杂系统并不一定能用线性模型描述，此时若要研究复杂系统的有限频段性能，则需将GKYP引理进行推广.将原始的GKYP引理推广到基于FM[29]和Roesser[30]模型的2维系统，奠定了2维系统有限频段研究的基础.随后，研究人员基于2维GKYP引理研究了2维系统有限频段的正实性[28]、H∞滤波[31]及模型降阶[32]等.对含多个子模态的混杂系统，文献[33]中将GKYP引理推广到Markov跳变系统，得到各子模态系统均满足有限频段性能指标的H∞控制器.

3 多模态系统有限频段性能研究进程

3.1 系统描述

多模态系统中，Markov跳变系统每一时刻所处的模态是随机的，其子模态之间的转换符合Markov过程.而切换系统模态间切换规则是确定的，因此切换系统可视为一类特殊的Markov跳变系统.下面将以连续时间Markov跳变系统为例介绍系统的数学模型.

在给定完备概率空间(Ω，F,P)下，考虑如下系统

(3)

其中：x(t)∈Rn为系统状态向量；u(t)∈Rm为系统输入向量；z(t)∈Rq为被控输出向量；w(t)为有限频段干扰输入；r(t)为系统模态，取值于有限集S={1,2,…,i,…,s}，在t时刻，r(t)=i,i∈S；A(r(t))，B(r(t))，Bw(r(t))，C(r(t))，Dw(r(t))为依赖于模态r(t)的适维矩阵.

连续系统的转移概率定义为

其中：λij为系统从t时刻模态i跳变到t+Δt时刻模态j的转移速率，λij≥0，且满足

特别地，对于离散Markov跳变系统，其转移概率定义为

πij=Pr{r(k+1)=j|r(k)=i}，

3.2 有限频段H∞控制

随着基于GKYP引理的有限频段理论的完善，H∞控制问题逐渐成为有限频段性能指标研究中的热点.

定义1在特定频段内，从干扰输入到被控输出的传递函数Gzw(jω)若满足

则认为系统满足有限频段H∞性能指标.

有限频段H∞控制问题可描述为：对于系统(3)，设计状态反馈控制器使系统在指定频段内满足H∞抗干扰性能指标.近年来，研究人员在多模态系统有限频段H∞控制上取得了如下成果：文献[34]对防震系统设计了状态反馈H∞容错控制器，用迭代算法得到了有限频段最优H∞性能指标.文献[35]将频段信息引入一致性协议设计，得到了模态依赖的有限频段一致性条件，能保证系统收敛于零时还具有有限频段H∞抗干扰性能.针对特定频段的噪声干扰，文献[32]将GKYP引理推广到Markov跳变系统，设计有限频段H∞控制器，使每个子模态系统均满足给定的H∞性能指标，得到原跳变系统也满足H∞性能指标的结论.考虑到转移概率部分未知的情况，文献[36]使用与GKYP引理等价的时域不等式，对Markov跳变系统进行了研究，以线性矩阵不等式的形式，给出了使系统渐进稳定且满足抗干扰性能指标的有限频段H∞控制器存在的充分条件.

3.3 有限频段H∞滤波

滤波在信号处理、目标跟踪及图像处理中扮演者不可或缺的角色，同时在控制理论中有非常重要的作用.

考虑系统

(4)

其中：x(t)为系统状态；y(t)和z(t)分别为测量输出和被控输出；w(t)为有限频段干扰输入；i为系统模态，取值于有限集S={1,2,…,s}；Ai，Bi，Ci，Di，Li均为依赖于模态i的适维矩阵.

针对系统(4)构造全维滤波器

(5)

其中：Afi，Bfi，Cfi为滤波器参数.

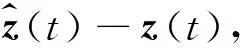
(6)

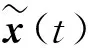
有限频段H∞滤波问题可描述为：对于给定的系统(4)，设计一组滤波器(5)，使误差系统(6)渐近稳定且满足有限频段H∞抗干扰性能指标.文献[37]研究了多胞不确定离散切换系统的有限频段H∞滤波问题，结果表明在干扰噪声频段信息已知的情况下，有限频段的滤波效果优于全频段.文献[38]为非线性系统设计了有限频段模糊滤波器，使误差系统分别在低、中、高频段满足相应的有限频段性能指标.文献[39]将不完全观测的网络控制系统建模为Markov跳变系统，并给出了保证系统满足有限频段性能指标的H∞滤波器存在的条件.文献[40]结合有限短时间理论，设计了基于Markov跳变系统有限频段滤波器，保证误差系统具有H∞干扰抑制水平的同时也满足有限时间有界，实现了时域、频域两个角度对系统的约束.文献[41]基于GKYP引理，给出了离散系统有限频段H∞滤波器存在的充分条件.文献[42]从信号角度研究了未知隶属度函数T-S模糊系统有限频段L2-L∞滤波问题，通过计算矩阵的迹给出了有限频段L2-L∞性能指标的新结果.文献[43]针对传感器非线性且转移概率部分未知的Markov跳变系统，设计了模态依赖的有限频段滤波器，以保证系统随机稳定且满足性能指标要求.

3.4 有限频段故障检测

故障信号和外界扰动信号往往具有明显的频率特性，且其频谱特点各不相同，因此在故障检测中综合考虑其有限频段特性，不仅可快速准确识别故障发生，还能提高系统的鲁棒性.

考虑系统

(7)

其中：x(t)为系统状态；y(t)为系统输出；w(t)和f(t)分别为有限频段干扰信号及故障信号；i是系统模态，取值于有限集S={1,2,…,s}；Ai，B1i，B2i，Ci，D1i，D2i均为依赖于模态i的适维矩阵.

针对系统(7)构造滤波器

(8)

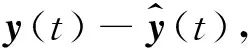
(9)

其中

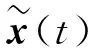
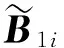
为实现故障检测，定义残差评估函数J(t)及阈值Jth分别为

当J(t)>Jth⟹故障，当J(t)

有限频段故障检测问题，即设计滤波器(8)使增广误差系统(9)在有限频段内满足下列条件：

(1) 增广误差系统渐近稳定.

(2)f(t)=0时，干扰输入w(t)到残差r(t)的传递函数Grw(jω)满足

其中：σmax(·)表示(·)的最大奇异值；γw为给定的干扰抑制性能指标；Ω为噪声的有限频段范围.

(3)w(t)=0时，故障信号f(t)到残差r(t)的传递函数Grf(jω)满足

其中：σmin(·)表示(·)的最小奇异值；γf为残差信号的故障敏感度性能指标；Ω为故障的有限频段范围.

文献[44]基于极点配置方法，为不确定离散系统设计了有限频段故障检测滤波器.文献[45]考虑传感器故障的多样性，建立了多模态T-S模糊系统，所设计的有限频段故障检测滤波器对传感器故障及输入参考信号故障均反应灵敏.文献[46]提出了时滞依赖有界实引理，通过构建超平面切线给出了多时滞不确定系统有限频段故障检测滤波器的设计条件.文献[47]基于平均驻留时间方法，研究了离散切换系统的有限频段故障诊断与隔离问题，对每个子系统均设计对应的滤波器，使残差信号只对该子系统有效.

数据丢包等非线性现象经常出现，故网络控制系统是一类常见的多模态系统.文献[48]针对量子化误差及Markov数据丢包，研究了网络控制系统随机故障检测问题，设计了相应的故障检测滤波器以保证系统的有限频段性能.针对信息进入信道的过程符合Markov链的情况，文献[49]提出了一种兼顾灵敏度及衰减性的网络控制系统的故障检测方法.文献[50]基于几何方法，给出了网络控制系统故障诊断及隔离滤波器的设计方法，使每个子滤波器与其他故障解耦.文献[51]结合帕塞伐尔定理与严格的S-procedure，设计了参数时变Markov跳变系统故障检测滤波器，使系统不仅具有较好的有限频段性能，还扩宽了可检测故障的范围.

3.5 有限频段性能研究的应用

目前，在有限频段性能研究的应用中，较为成熟的应用是汽车悬架系统的设计.文献[19]依据人体对外力较为敏感的频段为4～8 Hz的事实，基于状态反馈提出了汽车悬架系统的有限频段H∞控制器的设计方法，提高了该频段扰动的隔离效果，使行车体验更加舒适.考虑到系统状态难以完全可测及执行器的随机故障，文献[52]提出了汽车主动悬架系统有限频段动态输出反馈控制器的设计方法.对于驱动系统安装在轮毂处的电动汽车，其悬架系统簧下质量比其他类型汽车的要大，导致行车舒适性差且电机轴承磨损严重，针对此类情况，文献[53]综合考虑输入时滞及参数摄动等，研究了悬架系统的有限频段控制策略.针对参数不确性，文献[54]研究了汽车主动悬架系统的传感器容错控制问题，所设计的H∞控制器不仅能够减少4～8 Hz频段路面不平整对乘客的影响，还能保证车轮的动静载与悬架行程之比在允许的范围内.

有限频段性能研究也常用于振动抑制.文献[16]基于地震波大部分的能量集中在0.3～8 Hz频段，设计了状态反馈控制器，使建筑物在该频段的干扰抑制能力大大增强.文献[33]为建筑防震系统设计了有限频段状态反馈H∞容错控制器，用迭代算法得到了有限频段最优H∞性能指标，其设计方案比现有设计方案具有更好的振动抑制效果.有限频段分析与设计方法也应用于航天器的随机振动系统[55]及机械臂系统的设计.

4 总结与展望

虽然自GKYP引理提出以来，有限频段性能的相关研究得到了不少有意义的结果，但还存在需进一步探索的问题如下：

(1) 上述将GKYP引理推广并应用到多模态系统中的做法，虽然得到了较好的有限频段控制性能，但仅仅是根据对象特性将引理进行推广，或通过其他手段将多模态混杂系统转化成单模态线性系统，并没有从定理变形的角度给出严谨的数学证明，使GKYP引理适用于其他复杂动态系统.因此，从数学角度将GKYP引理推广到更一般的复杂系统，是最重要也是最具挑战性的课题.

(2) 目前多数研究均基于线性矩阵不等式理论，所得结果也仅仅实现了充分性，并没有实现必要性，仍具有很大的保守性.因此，如何得到有限频段性能问题的充要条件及寻求其他求解工具以降低结果的保守性，是今后重要的研究方向之一.

(3) 现有研究成果大多针对基础理论问题，对于先进控制策略的有限频段性能的研究还没有文献涉及.另一方面，随着工业化水平的提高，对工业生产会提出更苛刻的要求，不仅要求控制系统在某一频段具有给定的性能指标，更希望系统在不同频段满足不同的性能指标.因此，自适应有限频段问题、多频段性能综合问题等均是值得进一步研究的课题.

(4) 有限频段性能研究的现有成果中，虽然有小部分能解决实际应用问题，但此应用仅限于单模态线性系统.对于多模态混杂系统大多只是理论研究，如何跨越理论研究与工程应用间的鸿沟，将所得结果应用于复杂工程系统，是一个有重大应用价值的课题.

参考文献：

[1] SWORDER D, ROGERS R. An LQ-solution to a control problem associated with a solar thermal central receiver[J]. IEEE Transactions on Automatic Control, 1983, 28 (10): 971-978.

[2] YAN H, ZHANG Q. A numerical method in optimal production and setup scheduling of stochastic manufacturing systems[J]. IEEE Transactions on Automatic Control, 1997, 42 (10): 1452-1455.

[3] WU L, SHI P, GAO H, et al. Filtering for 2-D Markovian jump systems[J]. Automatica, 2008, 44 (7): 1849-1858.

[4] LIU M, HO D W C, NIU Y G. Stabilization of Markovian jump linear system over networks with random communication delay[J]. Automatica, 2009, 45 (2): 416-421.

[5] MARITON M. Jump linear systems in automatic control[M]. New York: Marcel Dekker, 1990.

[6] 郑大钟, 赵千川. 离散事件动态系统[M]. 北京: 清华大学出版社, 2001.

[7] SUN Z, GE S S. Switched linear systems: control and design[M]. London: Springer-Verlag, 2005.

[8] LIBERZON D, MORSE A S. Basic problems in stability and design of switched systems[J]. IEEE Control Systems Magazine, 1999, 19 (5): 59-70.

[9] BENGEA S C, DECARLO R A. Optimal control of switching systems[J]. Automatica, 2005, 41 (1): 11-27.

[10] KRASOVSKII N N, LIDSKII E A. Analysis design of controller in systems with random attributes[J]. Automatic & Remote Control, 1961, 22: 1021-1025.

[11] COSTA O L V, FRAGOSO M D, MARQUES R P. Discrete time Markov jump linear systems[M]. London: Springer, 2005.

[12] 李贤伟, 高会军. 有限频域分析与设计的广义 KYP 引理方法综述[J]. 自动化学报, 2016, 42 (11): 1605-1619.

[13] DU C, XIE L, GUO G, et al. A generalized KYP lemma based approach for disturbance rejection in data storage systems[J]. Automatica, 2007, 43 (12): 2112-2118.

[14] LIM J S, RYOO J R, LEE Y I, et al. Design of a fixed-order controller for the track-following control of optical disc drives[J]. IEEE Transactions on Control Systems Technology, 2012, 20 (1): 205-213.

[15] PIPELEERS G, SWEVERS J. Optimal feedforward controller design for periodic inputs[J]. International Journal of Control, 2010, 83 (5): 1044-1053.

[16] PASZKE W, ROGERS E, GALKOWSKI K. On the design of ILC schemes for finite frequency range tracking specifications[C]//Decision and Control (CDC), 2010 49th IEEE Conference on IEEE, 2010: 6979-6984.

[17] CHEN Y, ZHANG W, GAO H. Finite frequency control for building under earthquake excitation[J]. Mechatronics, 2010, 20 (1): 128-142.

[18] 林署炯, 曾平, 林鹏威, 等. 高速列车引起的地基土振动研究综述[J]. 石家庄铁道大学学报 (自然科学版), 2016, 29 (4): 40-46.

[19] SUN W, GAO H, KAYNAK O. Finite frequencyH∞control for vehicle active suspension systems[J]. IEEE Transactions on Control Systems Technology, 2011, 19 (2): 416-422.

[20] SUN W, ZHAO Y, LI J, et al. Active suspension control with frequency band constraints and actuator input delay[J]. IEEE Transactions on Industrial Electronics, 2012, 59 (1): 530-537.

[21] 赵长钟. 切换跳变系统的有限时间控制问题研究[D]. 无锡：江南大学物联网工程学院, 2015.

[22] ZHOU K, DOYLE J C, GLOVER K. Robust and optimal control[M]. New Jersey: Prentice Hall, 1996.

[23] HOULIS P, SREERAM V. A parametrized controller reduction technique via a new frequency weighted model reduction formulation[J]. IEEE Transactions on Automatic Control, 2009, 54 (5): 1087-1093.

[24] GHAFOOR A, WANG J, SREERAM V. Frequency-weighted model reduction method with error bounds for 2-D separable denominator discrete systems[C]//Proceedings of the 2005 IEEE International Symposium on Mediterrean Conference on Control and Automation, 2005: 525-530.

[25] GHAFOOR A, SREERAM V. A survey/review of frequency-weighted balanced model reduction techniques[J]. Journal of Dynamic Systems, Measurement, and Control, 2008, 130 (6): 758-767.

[26] CHOW Y L, HU Y B, LI X, et al. Mixed additive/multiplicativeH∞model reduction[J]. Journal of Dynamic Systems, Measurement, and Control, 2013, 135 (5): 051005.

[27] IWASAKI T, MEINSMA G, FU M. Generalized S-procedure and finite frequency KYP lemma[J]. Mathematical Problems in Engineering, 2000, 6 (2/3): 305-320.

[28] IWASAKI T, HARA S. Generalized KYP lemma: unified frequency domain inequalities with design applications[J]. IEEE Transactions on Automatic Control, 2005, 50 (1): 41-59.

[29] LI X, GAO H, WANG C. Generalized Kalman-Yakubovich-Popov lemma for 2-D FM LSS model[J]. IEEE Transactions on Automatic Control, 2012, 57 (12): 3090-3103.

[30] YANG R, XIE L, ZHANG C. Generalized two-dimensional Kalman-Yakubovich-Popov lemma for discrete Roesser model[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2008, 55 (10): 3223-3233.

[31] LI X, GAO H. Robust finite frequencyH∞filtering for uncertain 2-D systems: The FM model case[J]. Automatica, 2013, 49 (8): 2446-2452.

[32] LI X, LAM J, CHEUNG K C. GeneralizedH∞model reduction for stable two-dimensional discrete systems[J]. Multidimensional Systems and Signal Processing, 2016, 27 (2): 359-382.

[33] 周超洁, 栾小丽, 刘飞. 跳变系统在给定时间内的有限频段H∞控制[J]. 控制理论与应用, 2016, 33 (2): 251-256.

[34] ZHANG H, WANG R, WANG J, et al. Robust finite frequencyH∞static-output-feedback control with application to vibration active control of structural systems[J]. Mechatronics, 2014, 24 (4): 354-366.

[35] LUAN X, ZHOU C, DING Z, et al. Stochastic consensus control with finite frequency specification for Markov jump networks[J]. International Journal of Robust and Nonlinear Control, 2016, 26 (13): 2961-2974.

[36] SHEN M, YE D. A finite frequency approach to control of Markov jump linear systems with incomplete transition probabilities[J]. Applied Mathematics and Computation, 2017, 295: 53-64.

[37] DING D, YANG G. Finite frequencyH∞filtering for uncertain discrete-time switched linear systems[J]. Progress in Natural Science: Materials International, 2009, 19 (11): 1625-1633.

[38] DING D W, YANG G H. Fuzzy filter design for nonlinear systems in finite-frequency domain[J]. IEEE Transactions on Fuzzy Systems, 2010, 18 (5): 935-945.

[39] ZHAO X G, YE D, LONG Y. RobustH∞filter design for networked control systems with missing measurement in finite-frequency domain[C]//Mechatronics and Automation (ICMA), 2013 IEEE International Conference on, 2013: 1630-1635.

[40] 赵长钟, 栾小丽, 刘飞. 基于有限频段的Markov 跳变系统有限时间H∞滤波[J]. 控制理论与应用, 2015, 32 (3): 406-412.

[41] HELLANI D E, HAJJAJI A E, CESCHI R. New approach toH∞filtering for uncertain discrete-time linear systems in finite frequency domain[C]//American Control Conference (ACC), 2016 IEEE, 2016: 3638-3643.

[42] LI X J, YANG G H. Finite frequencyL2-L∞filtering of TS fuzzy systems with unknown membership functions[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2017, 47 (8): 1884-1897.

[43] SHEN M, YE D, WANG Q G. Mode-dependent filter design for Markov jump systems with sensor nonlinearities in finite frequency domain[J]. Signal Processing, 2017, 134: 1-8.

[44] ZHANG S, WANG Z, DING D, et al. On design of robust fault detection filter in finite-frequency domain with regional pole assignment[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2015, 62 (4): 382-386.

[45] LI X J, YANG G H. Fault detection in finite frequency domain for Takagi-Sugeno fuzzy systems with sensor faults[J]. IEEE Transactions on Cybernetics, 2014, 44 (8): 1446-1458.

[46] LI X J, YANG G H. Fault detection in finite frequency domains for multi-delay uncertain systems with application to ground vehicle[J]. International Journal of Robust and Nonlinear Control, 2015, 25 (18): 3780-3798.

[47] LI J, YANG G H. Fault detection and isolation for discrete-time switched linear systems based on average dwell-time method[J]. International Journal of Systems Science, 2013, 44 (12): 2349-2364.

[48] LONG Y, YANG G H. Fault detection for networked control systems subject to quantisation and packet dropout[J]. International Journal of Systems Science, 2013, 44 (6): 1150-1159.

[49] LONG Y, YANG G H. Fault detection in finite frequency domain for networked control systems with missing measurements[J]. Journal of the Franklin Institute, 2013, 350 (9): 2605-2626.

[50] LONG Y, YANG G H. Fault detection and isolation for networked control systems with finite frequency specifications[J]. International Journal of Robust and Nonlinear Control, 2014, 24 (3): 495-514.

[51] ZHAI D, AN L, LI J, et al. Fault detection for stochastic parameter-varying Markovian jump systems with application to networked control systems[J]. Applied Mathematical Modelling, 2016, 40 (3): 2368-2383.

[52] WANG R, JING H, KARIMI H R, et al. Robust fault-tolerantH∞control of active suspension systems with finite-frequency constraint[J]. Mechanical Systems and Signal Processing, 2015, 62: 341-355.

[53] 陈长征, 王刚, 于慎波. 含输入时滞的电动汽车悬架系统有限频域振动控制的研究[J]. 振动与冲击, 2016, 35 (11): 130-137.

[54] 郑晓园, 张皓, 王祝萍, 等. 具有执行器容错的汽车主动悬架系统有限频率H∞控制[J]. 控制理论与应用, 2017, 34 (9): 1136-1142.

[55] 张玉梅, 韩增尧, 邹元杰. 航天器随机振动设计载荷有限频段法研究[J]. 航天器工程, 2013 (1): 49-53.