基于遗传优化的小波神经网络风电功率预测

，

(安徽工程大学 电气工程学院，安徽 芜湖 241000)

长期以来，以石油、天然气、煤炭为代表的化石能源占据了人类使用的能源的绝大部分.由于缺乏有效的技术支持，以及绿色环保意识尚未普及，化石燃料燃烧所导致的温室效应和环境问题正在全球范围内蔓延.因此，风能等可再生清洁能源的开发和利用愈来愈成为国际社会共同关注的课题.2006年以后，中国风电发展进入高速时期，年新增风电装机占全球新增风电装机的比例从2006年的不足10%，跃升至2010年的49%，2010年累计风电并网运行装机达到3 100万千瓦[1]，预计到2020年，我国力争风电累计装机将达到2亿千瓦.

随着风电装机容量与日俱增，风力发电存在的问题也逐渐暴露出来.由于风力发电与地方的气象因素和地理环境有着密切的联系，而气象因素固有的不稳定性直接决定了风电场风电功率具有波动性和间歇性，这将对电网的稳定运行构成严重挑战.因此，提出一种高精度的风电功率预测模型是现代电力系统亟待解决的问题.风电预测的主要应用包括通过短期预测进行合理的经济调度、机组组合操作以及选择合适时机对风机进行维护[2].中期风电预测帮助风电场做季度发电计划以及安排大型检修活动等[3].长期风电预测则可以评估地区可能的年均发电量.风电预测对于调度安排系统的发电计划、保证电力系统的安全稳定运行、降低备用容量和运行成本以及对电力市场进行有效的管理等都具有重要意义[4].

近年来，关于风电预测方法已经有了很多的研究，主要分为三类：物理模型、统计模型和组合模型.其中统计模型是根据风电场历史测量数据及风电场周边测量数据建立统计学习模型.统计建模的优点在于模型简单、计算量少，且随着诸多数据挖掘算法的不断改进与兴起，预测精度不断提高，因此被广泛运用于当今风电功率预测.常用的统计学习模型包括时间序列分析模型、支持向量机(Support-vector Machine，SVM)模型、人工神经网络(Artificial Neural Networks，ANN )模型、卡尔曼滤波(Kalman Filtering，KF)法等机器学习方法.文献[5]采用多种预测模型进行组合预测，对结果进行加权求和得到比较理想的预测结果.文献[6]提出基于时序——支持向量机的预测方法，即用时间序列法建模，选取影响风电场风电功率最大的参数作为该预测模型的输入变量，同样也得到了良好的结果.统计预测的缺点在于需要一定的历史数据，对于缺乏历史数据以及新建的风电场，需要采用其他方法，而且长期预测中会积累误差[7].

物理模型利用大气运动方程[8]和天气特征预测风速，然后将风速转化为风电功率.例如，根据数值天气预报系统 (Numerical Weather Prediction,NWP ) 的风速、风向、气温和气压等数据，结合地区地表粗糙程度、风力机之间的尾流效应，建立物理模型，进而对风电功率进行预测[9].物理预测方法不依赖历史数据，能够对风电场发电功率进行中长期预测.不过，基于NWP的物理预测数学模型复杂、计算量大，其应用有一定的局限性.通常运用NWP与统计学相结合的方法提高NWP数据的精度，以及将历史数据和NWP数据结合建立组合预测模型进行风电功率预测[4].文献[10]研究了不同风电场的风速与风功率之间的关系，结果表明在一片区域中不同风电场之间的风速与风功率密切相关,通过建立风速与风功率之间的联系可以提高风速及风电功率的预测精度.文献[11]中采用3个不同空间尺度以及4种不同边界条件的WRF模型，用模糊理论判断各个模型输出的不确定度，把每个模型的输出代入人工神经网络进行加权得到最终预测结果，这种组合模型与单个模型相比的精度提高大约35% 左右.

1 相关知识

1.1 Weibull分布函数

由于风电场中风速和风电功率有很强的相关性，可以选择具有相似天气数据的日期进行预测以提高预测精度.选择中国某地2015年1月2日19:50:00～2015年1月3日10:40:00以及2015年1月4日16:20:00～2015年1月4日23:40:00两个时间段每隔10 min记录的数据作为训练样本，2015年1月4日23:50:00～2015年1月5日3:50:00的数据作为预测对象.对训练样本和测试样本的风速序列样本进行概率分布拟合，分析两者的相似性.

目前，对风速的概率分布拟合已经有相当多的研究，包括Rayleigh Distribution，Generalized Rayleigh Distribution，Lognormal Distribution，three-parameter Lognormal Distribution functions，three-parameter Weibull functions,以及bimodal Weibull functions等[12].其中Weibull Distribution(WD)是瑞典数学家Waloddi Weibull在研究材料破坏强度时提出的连续型概率分布，具有计算复杂度小、精度高、变换灵活的特点，广泛应用于各领域工程的可靠性分析当中.因此研究采用Two-parameter Weibull Distribution Functions来拟合风速的概率分布，其概率密度函数为：

(1)

其中x是随机变量，λ>0是尺寸参数，κ>0是形状参数.对应的累计分布函为：

F(x;κ,λ)=1-e-(x/λ)κ,

(2)

1.2 小波变换Wavelet Transform

小波变换常用于非平稳信号的分析，其具有多分辨分析的特点，可以有效地提取信号中的信息.通过伸缩以及平移运算以适应时频信号分析的要求，对信号进行多尺度细化，从而达到高频处时间细分，低频处频率细分.

(1)连续小波变换(Continuous Wavelet Transform,CWT)其原理是将已知的基本小波ψ(x)(Mother Wavelet) 的函数作τ位移，再在不同尺度α下与待测信号x(t)作内积进行比较，从而分析待测信号在各个时刻、各种局部范围的局部特性[12].

(3)

式中，a,b分别称为尺度参数和位移参数.

(2)对式(3)进行离散化处理即得离散小波变换(Discrete Wavelet Transform,DWT).

(4)

式中，T为信号长度；n、m与尺度参数a和位移参数b存在如下关系：a=2m,b=n2m[13].在信号的多分辨分析基础上，Mallat[14]等提出计算离散正交小波变换的快速算法.将信号x(t)正交投影到空间Vj和Wj可以得到对应分辨力J下的离散逼近信号Aj(t)和离散细节信号Dj(t).小波分解如图1所示.

即信号

式中，Aj(t)是近似信号；Dj(t)是细节信号.

1.3 小波-BP神经网络

前馈神经网络是一种结构简单，逼近能力强的人工神经网络，常用于风速和风电功率的预测.其网络结构为输入层、隐含层、输出层，具有非线性不确定性，理论上三层前馈神经网络可以逼近任意形式的连续函数[15].为拟合输入数据和输出数据的联系，需要建立各个神经元之间的权值和阀值.Werbos[16]等首次提出前馈神经网络的反向传播算法(Back Propagation Algorithm)，通过不断修正前馈神经网络的权值和阈值，以达到输出数据与真实数据的均方误差最小化.研究建立输入层含有4个神经元，隐含层含有5个神经元，输出层含有1个神经元的网络结构，小波-BP神经网络如图2所示.其训练过程为：

图1 多层分解过程图2 小波-BP神经网络

(1)前向传播(Forward Propagation).经小波分解后的风速序列A3、D1、D2、D3输入至神经网络的输入层，则第j个隐含层神经元的输入加权和为：

(5)

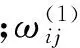
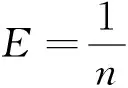
(6)

则隐含层与输出层之间的新权值可以表示为：

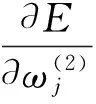
(7)

其中β是学习速率.

(8)

则输入层与隐含层之间的新权值可以表示为：

(9)

实际对小波-BP神经网络进行训练时存在如下问题：

①为最大程度逼近样本的性质，必须适当地选择隐含层神经元个数，以降低网络误差，提高精度，但隐含层神经元个数的最佳数量没有定论，通常做法是通过多次调整神经元个数，反复训练，选取最佳效果.

②网络的初始权值和阈值选择缺乏依据，而小波-BP神经网络连接权值和阈值的整体分布直接决定着数据拟合的效果.通常随机给定的各层之间的初始连接权值和阀值，用BP算法在训练中逐步进行修正，以获得一个较好权值和阀值分布[17].

③BP神经网络是基于梯度下降法的，不同的初始权值和阀值可能会导致网络不收敛或陷入局部极值点.

为提高预测精度，研究采用遗传算法来优化小波-BP神经网络的初始权值.

2 基于遗传优化的小波神经网络风电功率预测方法

由于风机的输出功率很大程度上受当地风速、风向、气压等自然因素的影响，而这些因素瞬息万变，导致风电功率数据具有很强的非平稳性.如果单纯地利用神经网络建立模型，只能拟合出系统的非线性，而数据的非平稳性将给预测结果带来误差.为提高预测精度，采用遗传优化的小波神经网络(AWNN-GA)来预测风电功率[18].首先将风速序列进行三层尺度的小波分解，将分解后的近似风速序列和细节风速序列作为人工神经网络的输入，对应的风电功率序列作为输出，用遗传算法优化人工神经网络的初始权值和阀值，进而做出精确的预测.

2.1 风速Weibull分布参数估计

对于WD中尺寸参数λ和形状参数κ的确定已有较多的研究，主要方法包括极大似然法(Maximum Likelihood Method,MLM)、矩量法(Method of Moments,MOM)[19]、标准偏差法(Standard Deviation Method,SDM)，Powerdensity Method[20]，The Graphical Method(GM)以及The Energy Pattern Factor Method(PDM)[21].研究采用相对成熟且精度较高的MLM来估计参数λ和κ.通过迭代方程获得尺寸参数λ和形状参数κ的具体值.迭代方程具体如下：

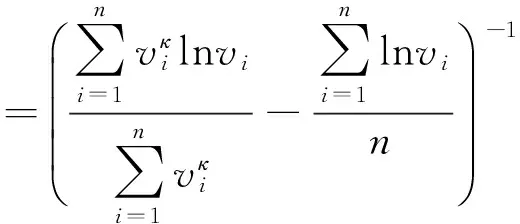
(10)

(11)

式中，vi是风速序列；n是风速序列总量.

2.2 拟合结果分析

训练样本及测试样本的累计分布情况如图3所示，概率分布情况如图4所示.由图3与图4可知，WD取得了比较理想的拟合效果，训练样本与测试样本具有较高的相似度，有助于提高预测精度.

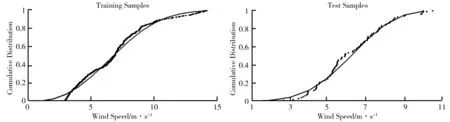
图3 风速累计分布

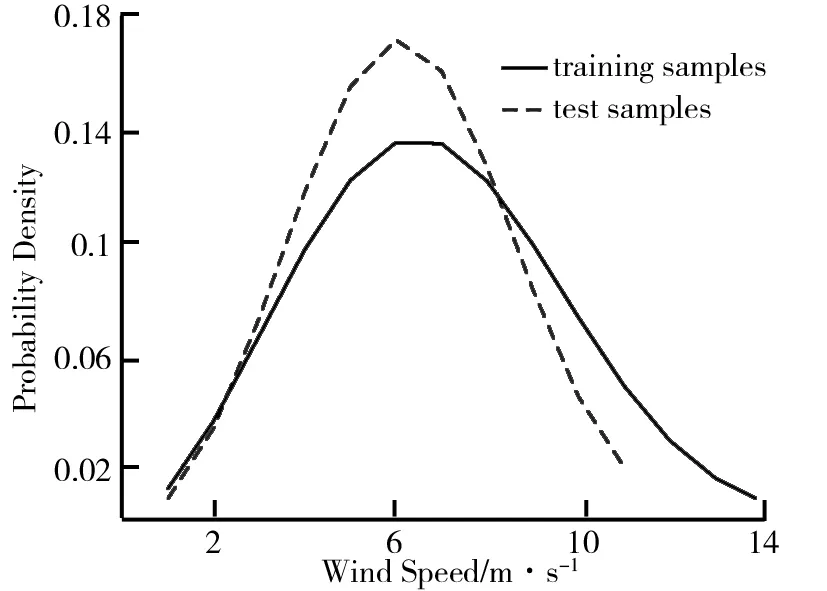
图4 风速概率分布

2.3 小波变换

采用6阶Daubechies小波函数(Wavelet Function of Type Daubechies of Order 6,Db6)作为母小波ψ(x)，对原风速序列进行3层尺度分解，分解结果如图5所示.

2.4 基于遗传优化的小波-BP神经网络

遗传优化的小波-BP神经网络流程图如图6所示.遗传算法(Genetic Algorithm,GA)是一种模仿生物进化原理的群体搜索(寻优)算法.其实质是根据自然选择原理，通过基因变异以及遗传操作不断进化出适应度更高的个体，从而找到最优解.GA具有简单稳定的特性，特别适合于大规模数据处理以及非线性优化模型[22].其具体过程如下：

图5 风速序列三层尺度分解

图6 遗传优化的小波-BP神经网络流程图

(1)随机产生初始权重参数和阀值参数，采用二进制编码对权重和阀值进行编码.

(2)确定适应度函数.以AWNN-BP的预测结果和真实数据之间的均方误差MSE的倒数作为适应度函数F.

(3)确定GA参数.采用的最大迭代次数为50，种群数目为40，基因突变概率为0.001，基因交叉概率为0.9.

(4)选择若干适应度高的个体作为双亲养殖后代.使用轮盘赌法进行选择操作，每个个体遗传到下一代的概率为该个体的适应度与整个群体的适应度之和的比，即

(12)

式中，Pi为个体被选择的概率；Fi为个体的适应度.这样，适应度高的个体会有更大的概率被选择.

(5)交叉运算.采用单点交叉运算，首先对选择的个体进行随机配对，并随机选择交叉点，进行染色体交叉.

(6)变异运算.在选择的个体上随机选择一个变异点，以基因变异概率将变异点的原有基因值取反.

(7)经过式(3)、式(4)和式(5)得到的子代包含了父代的优良特性，且适应度高于父代.重复上述步骤直至最大迭代次数.

(8)将得到的权值和阀值的二进制代码进行解码，作为小波-BP神经网络各层之间的初始权值和阀值.

2.5 仿真实验结果分析

用WBPNN-GA模型和BPNN模型分别进行预测，预测结果如图7、图8所示.

图7 AWNN-BP风电功率预测结果图8 BPNN风电功率预测结果

绝对预测误差为：

×100%，

式中,vc为电功率预测输出，vd为电功率实际值.结果如图9所示.

由预测结果可以看出，用GA优化的AWNN-BP的绝对预测误差明显小于FFNN-BP，前者具有更高的预测精度和工程应用价值.

图9 WBPNN-GA和BPNN绝对预测误差条形图

3 结论

根据对某地区未来15 h风电功率预测的研究可以得出：Weibull分布有着良好的概率密度和累计分布拟合效果，可以用其挑选出相似的风速数据进行预测，从而减小预测误差.改进的AWNN结合了遗传算法优良的并行运算能力、小波分解法对信号的时频分析能力以及BP 神经网络强大的非线性映射能力，因此具有较高的预测精度.受限于模型的性质，当预测时间增加时，预测精度明显下降.提出一种中长期电功率的预测方法是当今电力系统重要的研究方向.

[1] 国家发展和改革委员会能源研究所.中国风电发展路线图2050[EB/OL].www.cnrec.org.cn/cbw/fn/2014-12-29-459.html,2017-09-10.

[2] J M LUJANO-ROJAS,G J OSRIO,J C O MATIAS,et al.A heuristic methodology to economic dispatch problem incorporating renewable power forecasting error and system reliability[J].Renewable Energy,2016,87:731-743.

[3] 陈妮亚.短期风电功率预测方法研究[D].北京：北京航空航天大学，2014.

[4] 钱政,裴岩,曹利宵,等.风电功率预测方法综述[J].高电压技术,2016,42(4):1 047-1 060.

[5] 刘纯,范高锋,王伟胜，等.风电场输出功率的组合预测模型[J].电网技术,2009,33(13):74-79.

[6] 栗然,柯拥勤,张孝乾，等.基于时序——支持向量机的风电场发电功率预测[J]. 中国电力,2012,45(1):64-68.

[7] 符金伟,马进,周榆晓,等.风电功率预测研究方法综述[J].华东电力,2012,40(5):888-892.

[8] H LIU,H Q TIAN,C CHEN,et al.A hybrid statistical method to predict wind speed and wind power[J].Renewable Energy,2010,35(8):1 857-1 861.

[9] 文明，王志忠，郑岳怀，等.基点气象相似聚合的短期风电功率预测方法[J].电测与仪表,2016,53(5):74-79.

[11] J ZHAO,Z H GUO,Z Y SU,et al.An improved multi-step forecasting model based on wrf ensembles and creative fuzzy systems for wind speed[J]．Applied Energy,2016,162:808-826.

[12] A N CELIK,MOHAN KOLHE.Generalized feed-forward based method for wind energy prediction[J].Applied Energy,2013,101:582-588.

[13] 陈忠.基于BP神经网络与遗传算法风电场超短期风速预测优化研究[J].可再生能源,2012,30(2):32-36.

[14] 潘迪夫，刘辉，李燕飞.风电场风速短期多步预测改进算法[J].中国电机工程学报,2008,28(26):87-91.

[15] 阎平凡,张长水.人工神经网络与模拟退化计算[M].北京: 清华大学出版社,2005．

[16] P WERBOS.Beyond regression:new tools for predicition and analysis in the behavioral sciences[M].Cambridge,Boston:Harvard University,1974.

[17] 刘春艳,凌建春,寇林元,等. GA-BP神经网络与BP神经网络性能比较[J].中国卫生统计,2013,30(2):173-176,181.

[18] 王丽婕，冬雷，廖晓钟,等.基于小波分析的风电场短期发电功率预测[J].中国电机工程学报,2009,29(28):30-33.

[19] ORHAN KAPLAN,MURAT TEMIZ.A novel method based on weibull distribution for short-term wind speed prediction[J].International Journal of Hydrogen Energy,2017,42(28):17 793-17 800.

[20] KASRA MOHAMMADI,SHAHABODDIN SHAMSHIRBAND,POR LIP YEE,et al.Predicting the wind power density based upon extreme learning machine[J].Energy,2015,86:232-239.

[21] ILHAN USTA.An innovative estimation method regarding weibull parameters for wind energy applications[J].Energy,2016,106:301-314.

[22] LIMIN MA,SHIPENG HU,MIN QIU,et al.Energy consumption optimization of high sulfur natural gas purification plant based on back propagation neural network and genetic algorithms[J].Energy Procedia,2017,105:5 166-5 171.