基于简化粒子群优化的高铁钢轨智能检测技术*

王 曼，王 姮，张 华

(西南科技大学 特殊环境机器人技术四川省重点实验室，四川 绵阳 621010)

0 引言

近年来，随着列车承载量和速度的提高，铁路养护变得至关重要，而钢轨表面缺陷检测是铁路养护重要的环节，由于列车负载、碾压、自然环境等多种因素影响，轨面不可避免地出现轧痕、轧疤等缺陷。轨面缺陷如果不及时检测、维护，将会是很大的安全隐患[1]。

目前用于铁轨缺陷检测的无损检测技术中，机器视觉检测效率高，成本低，抗干扰性强，在铁轨表面缺陷检测中的应用得到了很好的发展[2]。2015年，文献[3]提出局部对比度测量法和最大熵法来对铁轨图像进行对比度增强和自动阈值分割。该方法对背景区域进行大量的均衡化，消除噪声的同时也丢失了大量的缺陷信息，使得分割缺陷轮廓模糊，严重失真。

2016年，文献[4]采用背景差分与自适应阈值相结合的方法实现钢轨表面缺陷分割，这种方法仅考虑灰度信息，鲁棒性较差，易受随机噪声的干扰。文献[1]中提出的基于模糊超熵与遗传算法实现轨面分割，采用Hough变换提取钢轨表面有效区域，再结合模糊熵理论得到图像的熵值，依据遗传算法得到最优分割阈值。这种方法复杂度高，算法较为耗时，很难满足实时性要求。

针对上述机器视觉缺陷检测方法存在速度慢、鲁棒性差、缺陷信息丢失的缺点，本文采用二维OTSU阈值的方法提高算法的自适应性，同时结合粒子群优化方法搜索得到最佳阈值，很大程度上提高了分割算法的速度和精度，满足实时性要求。实验证明，该方法鲁棒性好，可以处理低对比度、包含阴影和锈迹的钢轨缺陷图像，能够为后续的缺陷识别奠定良好的基础。

1 二维OTSU模型

早期的分割算法大多是基于一维灰度直方图选择阈值，其中著名的OTSU[5-6]法广泛应用于实时处理，但该方法仅适用于目标与背景具有高对比度和信噪比的图像，对于对比度和信噪比低的情况，OTSU法的分割精度较差。二维直方图是结合灰度值和像素邻域均值形成的联合直方图，同时考虑灰度信息和邻域空间信息。为了克服一维OTSU分割法对噪声和图像对比度较为敏感的缺点，二维直方图是结合灰度值和像素邻域均值形成的联合直方图，同时考虑灰度信息和邻域空间信息。基于二维直方图产生了二维OTSU阈值分割算法，该算法改善了一维OTSU分割法的抗噪性和低对比度图像的敏感性。

该方法描述如下：给定一幅大小为m×n的图像，图像的灰度级为L，像素数量为N=m×n，(x,y)处的灰度值为i，其邻域内灰度均值为j，nij表示(i,j)在一幅图中出现的次数，Pij表示(i,j)的概率分布，计算方式如下：

Pij=nij/N,i,j=0,1,2,…,L-1

(1)

在二维OTSU模型中定义图像的阈值为联合向量(t,s)，阈值将图像划分为目标A和背景B两个区域，A和B两个区域内的概率分布如下：

(2)

A和B均值向量为：

(3)

在二维直方图中的概率分布如下：

μT≈wAμA+wBμB

(4)

A和B两类间离散矩阵为：

Sb(t,s)=wA(μA-μT)(μA-μT)T+wB(μB-μT)(μB-μT)T

(5)

离散矩阵的迹如下：

trSb(t,s)=wA[(μAi-μTi)2+(μAj-μTj)2]+wB[(μBi-μTi)2+(μBj-μTj)2]

(6)

离散矩阵的迹的最大值(T,S)则为二维OTSU模型的最优阈值。

2 简化粒子群优化

简化粒子群优化方法(Simple Particle Swarm Optimization，SPSO)是一种简单、高效、灵活的群优化方法。相比于PSO(Particle Swarm Optimization)[7-8]和GA[9]，SPSO算法探测最优解具有更好的鲁棒性且更高效。SPSO算法广泛应用于谐波问题[10]和ANN学习率问题[11]等。

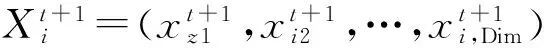
SPSO的更新规则如下：

(7)

这里λ服从[0,1]均匀分布，x是第i个变量的解区间内的一个随机值。Cw、Cp和Cg是给定的常数。

在PSO中等式(7)的Pbest_i和Gbest_i概念是相同的。Pbest_i可以搜索得到局部最优解，Gbest_i则能跳过局部最优得到全局最优解[11]。

在SPSO中舍弃粒子的速度，每一次迭代粒子从当前位置跳到其他位置或者仍旧保留在原位置，或者在同等维数的其他位置。在更新过程中，这种跳跃和更新使得所有粒子在解空间搜索得到最优解。SPSO算法没有设定粒子速度参数，可以避免因设定该参数而影响粒子的收敛速度和搜索精度。

3 基于SPSO的二维OTSU算法

在SPSO基础上，本文提出了结合离散化SPSO和二维OTSU阈值化方法获得最佳阈值的改进方法。SPSO中适应度函数的输入是连续值，为了将SPSO算法应用于图像阈值化问题，首先要将其扩展至离散空间，即使得输入值为离散值。

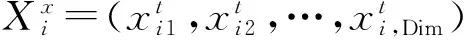
(8)

二维OTSU模型的解属于二维空间，如下式：

(9)

基于SPSO的二维OTSU阈值化方法步骤如下：

(1)令t=1,随机生成Xi。通过二维OTSU模型的等式(6)计算F([Xi,1])合理度值，搜索F([Xi,1])中的最优解F([Gi])，其中i=1,2,3,…,POP。

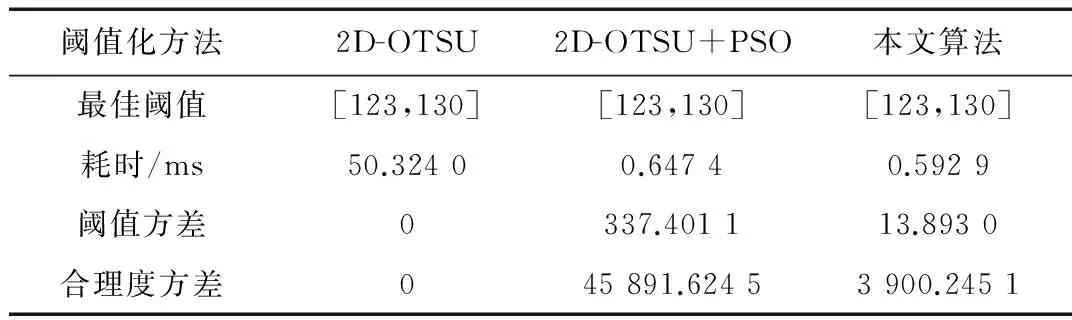
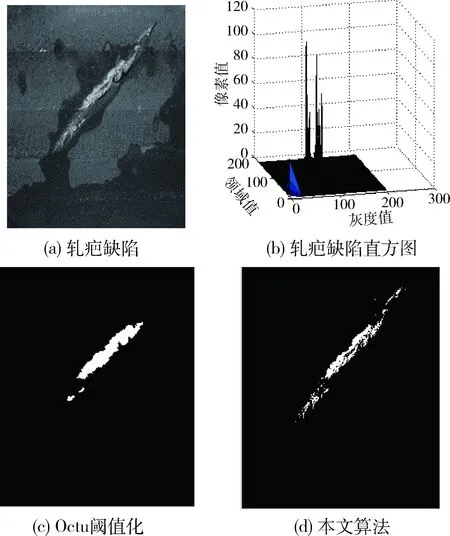
(2)当i

①依据等式(7)更新，采用二维OTSU模型计算的合理度值；

②如果当前合理度值优于F([Pi])，则令Pi=Xi，否则，执行步骤④；

③如果当前位置最优解Pi优于粒子群中最优解Gi，则令Gi=Pi；

④i=i+1,执行步骤②。

(3)如果t循环至最大迭代次数循环终止，则Gi为最终阈值，否则令t=t+1返回步骤(2)。

4 实验结果与分析

在本实验中对传统的枚举二维OTSU算法和基于PSO的二维OTSU方法与本文算法加以比较，本实验中PSO和SPOS的粒子数(Population of Particle,POP)为27。两者的最大迭代次数均为50。PSO的权重系数ω为0.6，加速系数C1和C2为1.67。在SPSO中，Cω=0.19，Cp= 0.44，Cg=0.7,PSO和SPSO算法都通过随机初始化100次实现。

为便于比较PSO和SSO搜索能力，阈值的方差和二维OTSU类间离散矩阵的迹的方差定义如下：

(10)

(11)

这里ti是搜索法阈值和枚举法阈值的差，即：ti=tPSO/SSO-tOTSU；γ=ti/k；fi是搜索法的迹的值和枚举法的迹的值之差，即fi=fPSO/SSO-fOTSU;υ=ti/k；k是PSO和SPSO的初始化次数，这里k=100。

两种缺陷图像的耗时、阈值方差、合理度方差等统计结果如表1和表2所示，可以看出在相同的灰度阈值和邻域均值条件下，本文算法运算速度最快，耗时最短。此外，依据方差信息可以证明本文算法鲁棒性较好，自适应性强。

表1 轧疤缺陷的参数值计算

表2 轧痕缺陷的参数值计算

为了验证本文方法的有效性，使用传统算法和本文算法进行对比实验。第一幅测试图像选择低对比度的钢轨轧疤缺陷图像，如图1(a)所示，图1(b)是图1(a)对应的二维直方图，图1(c)是传统的OTSU分割结果，本文算法的分割结果如图1(d)所示。实验结果表明：传统方法受图像对比度的影响，并未准确地将目标与背景进行分割，而本文算法结合灰度和空域信息使得分割精度显著提高，同时采用SPSO加快阈值搜索，减少了计算复杂度，实验结果显示背景与缺陷分割更加准确，同时缺陷信息得到了有效保留。

图1 轧疤缺陷图像分割

第二幅测试图像是含有大面积阴影、锈迹的钢轨轧痕缺陷的图像，如图2(a)所示，图2(b)是图2(a)对应的二维直方图,图2(c)是传统的OTSU分割结果。可以看出传统方法没有将缺陷完整地分割出来，丢失了大量的缺陷信息，本文算法的分割结果如图2(d)所示，分割得到的缺陷轮廓、位置、面积等必要信息准确地保留下来。因此本文算法在运算速度和分割精度两个方面均优于传统分割方法。

图2 轧痕缺陷图像分割

5 结论

SPSO算法是一种模拟自然界生物行为的优化系列算法，该方法仅需基本的数学操作，无需梯度信息，理论研究和应用意义都足以证明SPSO算法是一种能够有效解决全局优化问题的新方法。本文首次提出基于SPSO的钢轨表面缺陷图像阈值分割方法。该方法融合SPSO速度快和二维OTSU阈值化精度高两大优势，实现了钢轨缺陷图像的准确分割。

本文方法不受钢轨缺陷图像对比度、阴影、锈迹等因素的影响，实验结果与实际相符，足以证明本文提出的算法具有很高的应用价值。后期工作主要是结合深度学习方法对分割得到的缺陷加以分类识别，以满足在线智能化需求。

[1] 程天栋，闵永智，马宏锋.基于模糊超熵与遗传算法的轨面缺陷分割算法[J].兰州交通大学学报，2016，1(6):46-50.

[2] 贺振东，王耀南.毛建旭，等.基于反向P-M扩散的钢轨表面缺陷视觉检测[J].自动化学报，2014，40(8)：1667-1679.

[3] 邬锋，茅正冲.铁轨表面缺陷图像增强与分割算法[J].计算机仿真,2015,32(10):159-162.

[4] 贺振东，王耀南，刘洁.基于背景差分的高铁钢轨表面缺陷图像分割[J].仪器仪表学报, 2016, 37(3): 640-649.

[5] 徐少平，刘小平，李春泉.基于区域最大相似度的快速图像分割算法[J].光电子·激光, 2013,24(5):990-998.

[6] 郭瑞.基于模糊聚类的图像分割方法的研究[D].长春：吉林大学，2015.

[7] 胥小波，郑康锋，李丹.新的混沌粒子群优化算法[J].通信学报, 2012, 33(1):24-30.

[8] 金敏，鲁华祥.一种遗传算法与粒子群优化的多子群分层混合算法[J].控制理论与应用, 2013, 30(10):1231-1238.

[9] 于莹莹，陈燕，李桃迎.改进的遗传算法求解旅行商问题[J].控制与决策, 2014(8):1483-1488.

[10] YEH W C, New parameter-free simplified swarm optimization for artificial neural network training and its application in the prediction of time series[J]. IEEE Transactions on Neural Networks and Learning Systems,2013,24(4): 661-665.

[11] YEH W C, HUANG C L. Simplified swarm optimization to solve the K-Harmonic means problem for mining data[C]//Proceedings of the 18th Asia Pacific Symposium on Intelligent and volutionary Systems, 2015:429-439.