基于费用函数的测试性指标优化分配方法
2018-03-29朱智平王贵腾王鸿睿杨庆国
王 贺,朱智平,王贵腾,王鸿睿,杨庆国
(湖南云箭集团有限公司,湖南 长沙 410100)
0 引言
随着电子技术的发展,制导航空炸弹体制越来越多,其弹上电子设备和技术也越来越复杂。为保证制导航空炸弹成功执行任务,需要在投放前对其进行充分的性能测试。良好的测试性,可以快速准确地检测、隔离故障,在载机投放前或挂机前就能发现、定位问题,可以大大减少载机因炸弹故障而带弹返回和炸弹投放之后的任务失败。因此,测试性作为制导航空炸弹的一项重要设计指标,对制导航空炸弹的使用起着非常关键的作用[1-2]。
在进行制导航空炸弹测试性设计时,首先要进行测试性分配,将测试性指标自上而下地分配给各组成单元。目前,常用的测试性分配方法有故障率分配法、加权分配法、综合加权分配法、层次分析法、优化分配法等[3]。故障率分配法中,故障率高的组成单元应有较高的故障检测率与隔离率,反之应分配较低的故障检测率与隔离率。加权分配法考虑系统测试性参数受众多因素的影响,为每个影响因素设置权重,依据每个产品加权值占总加权值的比例求解分配值。综合加权分配法在加权分配法的基础上考虑了影响因素的重要程度,引入了影响因素加权值。层次分析法将所分析的问题按级分层,通过对层内元素之间相互影响关系的分析,得出最佳决策[4-5]。优化分配法以构造的目标函数为基础,求其最大值或最小值,从而实现优化分配[6-7]。
在给定系统测试性指标而现有系统方案不满足要求的情况下,测试性工程人员面临做出对哪些组件进行改进的决定,从而使全部实现费用最小。优化分配法协调系统各组成单元之间费用、体积、重量等因素,可以在总费用最小这一目标前提下,将测试性指标分配给各组成单元。
采用总费用最小作为优化目标,需建立总费用与各组成单元测试性指标之间的模型。但在很多情况下,这些模型在参数合理、准确量化与精确求解方面并不容易实现[8-9]。针对该问题,提出了一种容易量化参数的费用函数,并采用遗传算法求解该问题,可以求得高精度的分配结果。
1 测试性分配模型
设系统由n个单元组成,系统要求的测试性指标为Psr,在总费用最低的情况下将该指标分配给各组成单元,这一问题的数学模型为[10]:
(1)
(2)
Ps≥Psr
(3)
Pi,min≤Pi≤Pi,max
(4)
式(1)中,Pi为分配给组成单元i的测试性指标(具体为故障检测率或故障隔离率);c(Pi)为组成单元i的费用函数;C为系统总费用。式(2)中,Ps为由各组成单元分配的测试性指标计算得出的系统测试性指标,λi为组成单元i的故障率。式(3)中,Psr为系统要求的测试性指标。式(4)中,Pi,min为组成单元i当前达到的最低测试性水平;Pi,max为组成单元i可以达到的最高测试性水平。
求解这一模型,首先需要获取系统的参数,然后建立各组成单元测试性和费用之间的函数关系,最后求解费用函数。
2 费用函数
2.1 费用函数的基本要求
Dale 和Winter提出了费和函数必须满足的基本条件[11]:

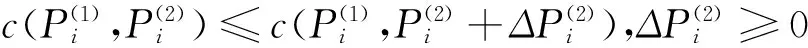
(3)c(Pi)可微;
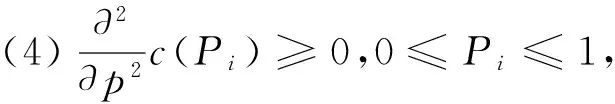
(6)c(Pi)为单调递增函数。
2.2 费用函数模型
根据费用函数的基本要求,提出了一种费用函数模型:
(5)
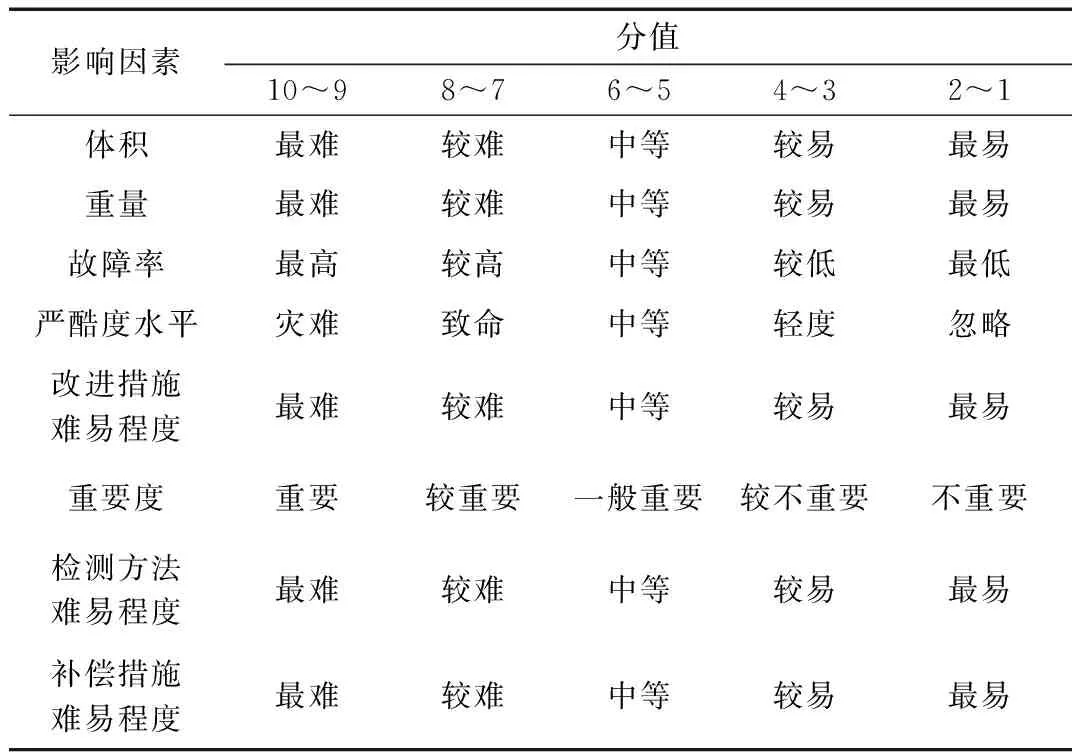
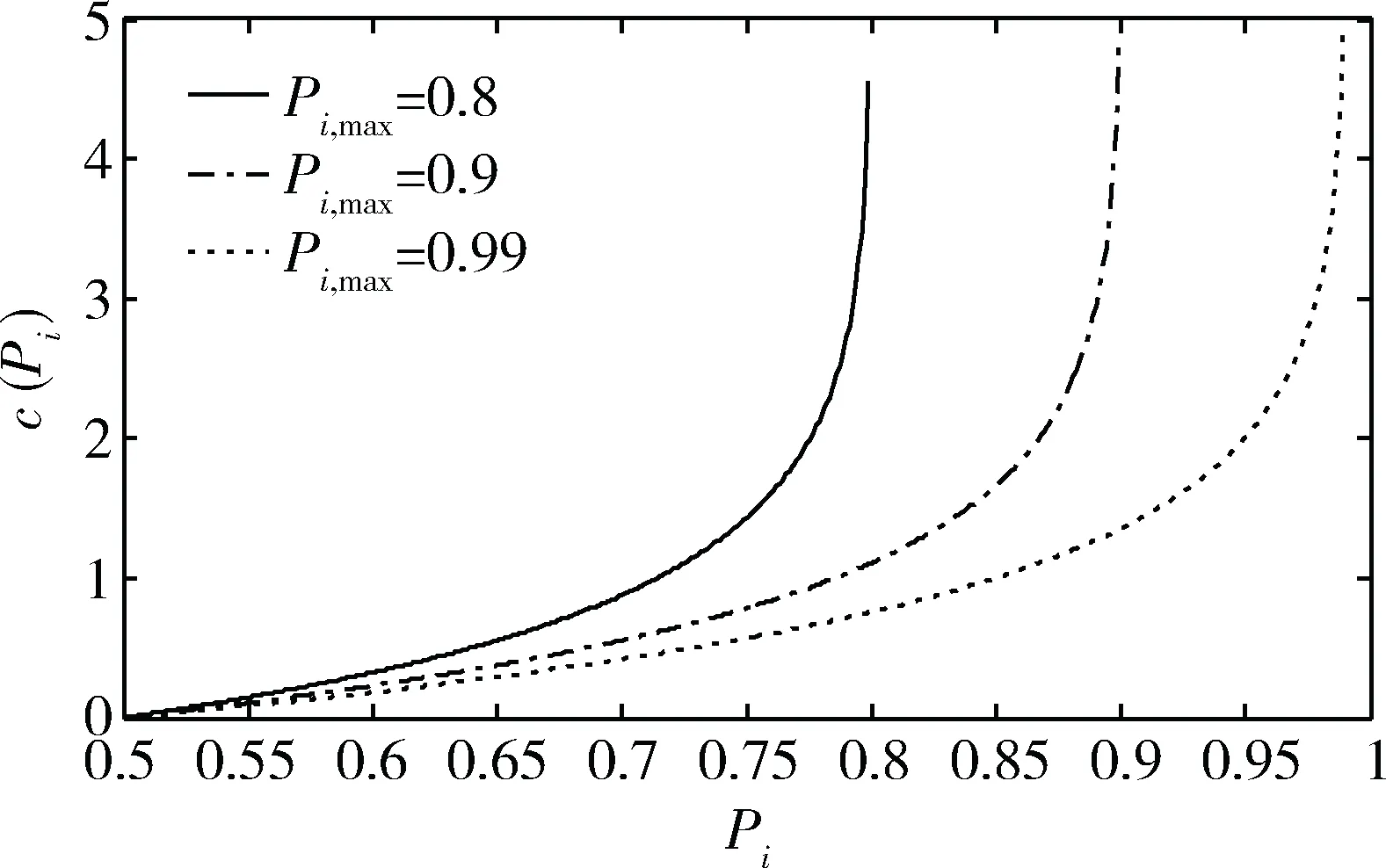
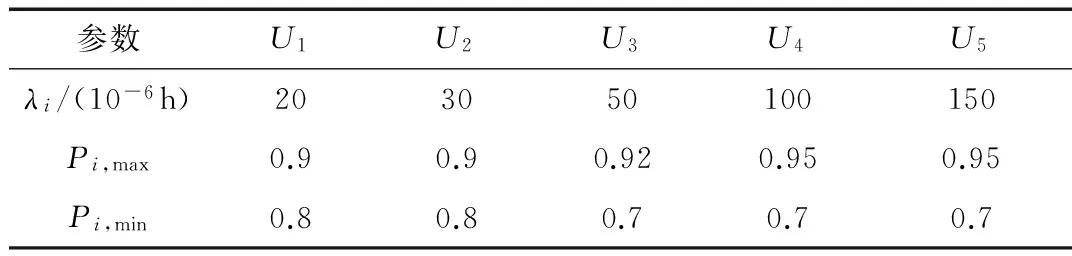
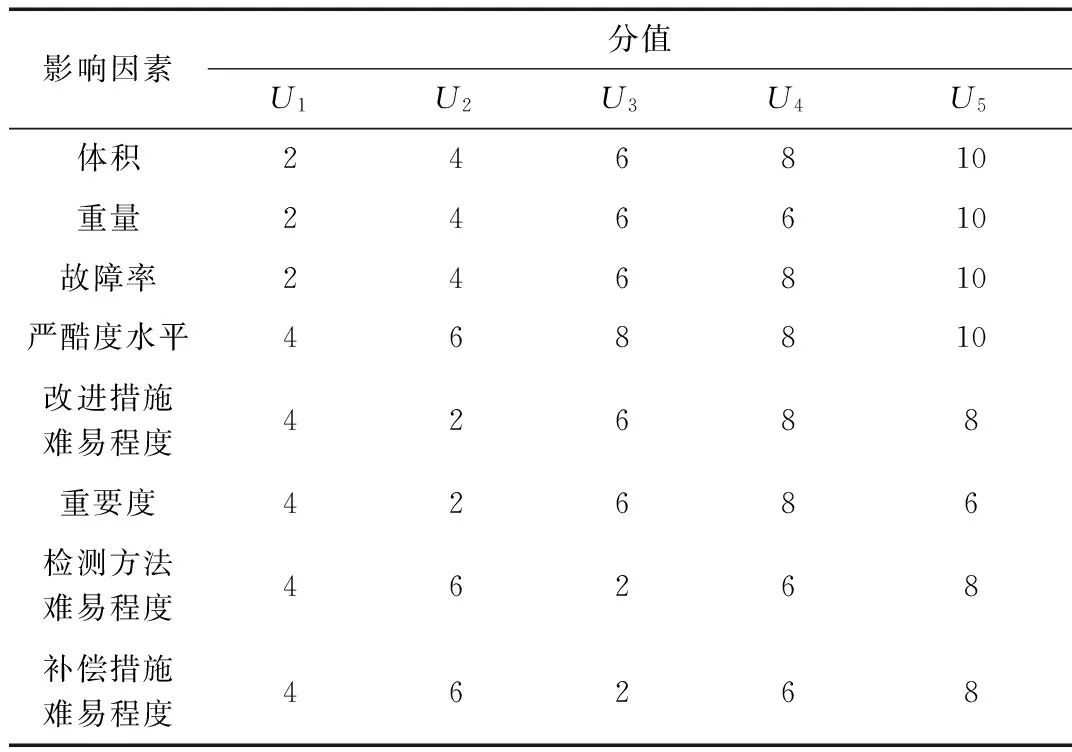
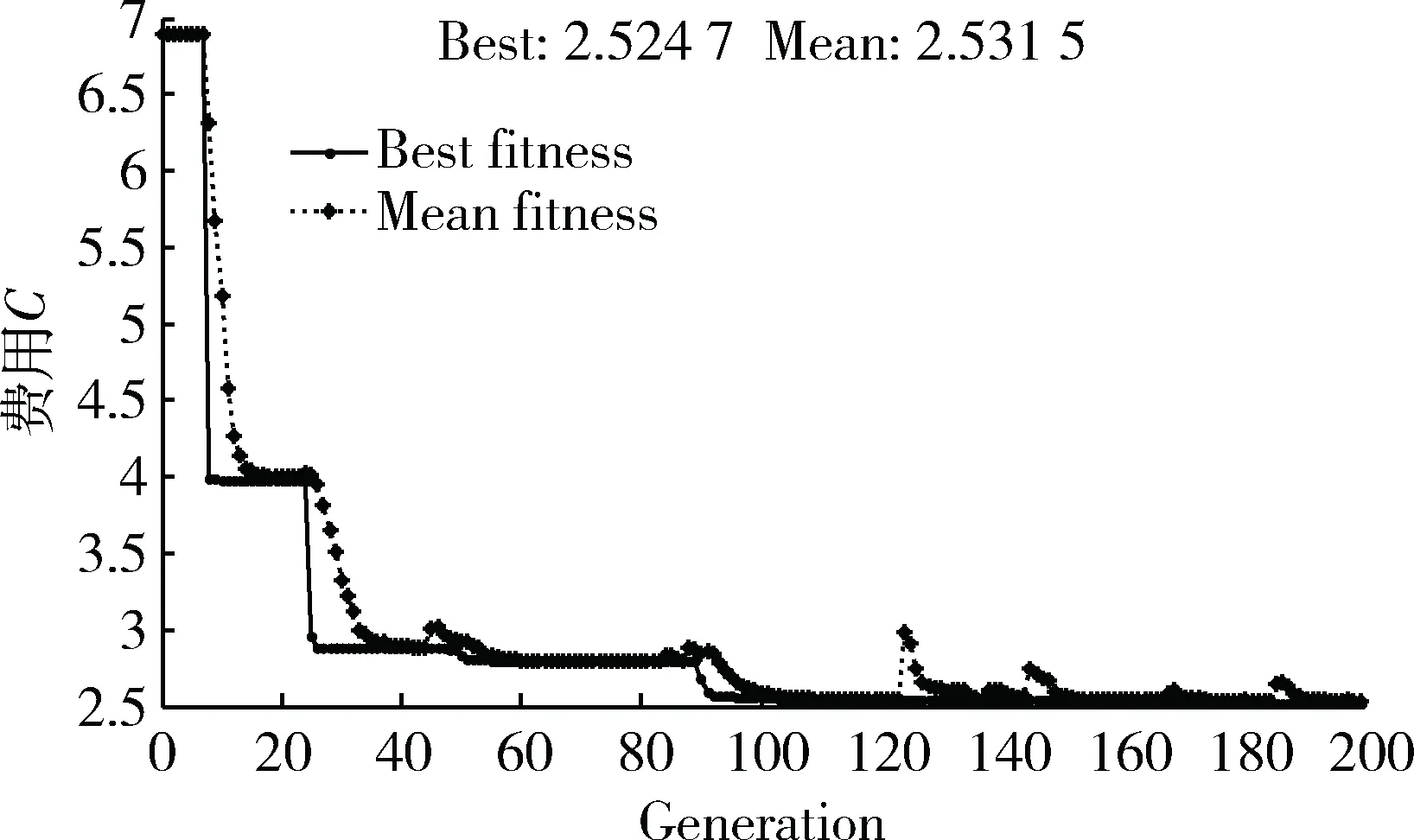
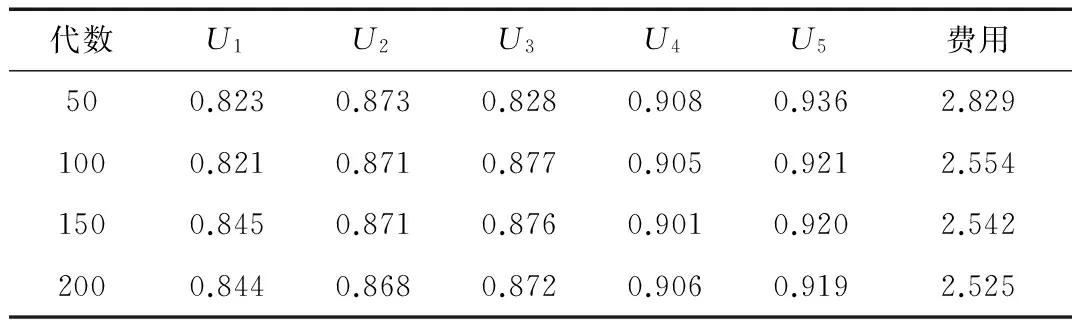
式中,fi为提高组成单元i的测试性水平的费用系数,0 例如,取fi=0.8,Pi,max=0.99,Pi,min=0.5,c(Pi)随Pi的变化曲线如图1所示。 图1 费用函数曲线图 由图1可以看出,费用函数模型有以下特点: (1)费用是关于组成单元的非线性单调递增函数; (2)达到高测试性水平所需的费用很高,要达到最高测试性水平Pi,max,理论上所需费用为无限大,在实际工程中则意味着费用非常高; (3)要求的测试性水平越高,费用增长越大。例如,一个组成单元测试性水平从0.6增加到0.7要比从0.8增加到0.9更容易。 费用系数为常量,用以表征相对于系统中其他组成单元,提高本组成单元所需费用大小的程度。 例如,取Pi,max=0.99,Pi,min=0.5,fi分别取0.1,0.5,0.9,c(Pi)随Pi的变化曲线如图2所示。 图2 不同费用系数fi下费用函数曲线图 由图2可以看出,费用系数越大,曲线越陡,费用变化越快速;反之,费用变化越缓慢。 测试性优化分配的影响因素很多,主要包括:体积、重量、设计成本、维修费用、故障率等。其中,设计成本主要考虑严酷度水平、设计改进措施的难易程度以及重要度;维修费用主要考虑故障发生时检测方法的难易程度和使用补偿措施的难易程度。采用专家评分法评分,评分标准如表1所示。 表1 影响因素评分标准 根据影响因素评分表得到影响因素评分向量: Ai=[ai1,ai2,ai3,ai4,ai5,ai6,ai7,ai8] (6) 式(6)中,Ai为组成单元i的测试性影响因素评分向量;ai1~ai8为组成单元i的表1中各影响因素评分值。 各个影响因素对不同的组成单元测试性的影响程度不同,需根据实际情况给定影响因素权值。采用专家评分法评分,将权重分为5个等级:很重要(10~9)、较重要(8~7)、一般重要(6~5)、较不重要(4~3)、很不重要(2~1),并得到影响因素权重向量: ωi=[ωi1,ωi2,ωi3,ωi4,ωi5,ωi6,ωi7,ωi8] (7) 式(7)中,ωi为组成单元i的测试性影响因素权重向量;ωi1~ωi8为组成单元i的表1中各影响因素权重值。 完成影响因素和影响因素权重的评分后,进行加权平均并归一化,得出费用系数。费用系数计算公式如下: (8) 可达到的最高测试性水平为常量,用以表征在现有理论和技术条件下,组成单元可以达到的测试性水平的极限值。最高测试性水平的理想值为1,但是,受技术或经济方面的限制,一般达不到。 例如,取fi=0.8,Pi,min=0.5,Pi,max分别取0.8,0.9,0.99,c(Pi)随Pi的变化曲线如图3所示。 图3 不同Pi,max下费用函数曲线图 由图3 可以看出,Pi,max越大,曲线越平, 费用变化越缓慢;反之,费用变化越快。 当前达到的测试性水平为常量,用以表征组成单元已经达到的测试性水平。所有组成单元当前测试性水平的极限值为0。 例如,取fi=0.8,Pi,max=0.99,Pi,min分别取0.1,0.4,0.7,c(Pi)随Pi的变化曲线如图4所示。 图4 不同Pi,min下费用函数曲线图 由图4 可以看出,Pi,min越大,曲线越陡,费用变化速度越快;反之,费用变化越缓慢。 遗传算法(Genetic Algorithm, GA)是一种基于生物遗传和进化机制的适合于复杂系统优化的自适应概率优化技术。遗传算法从任一种群出发,通过选择、交叉、变异,产生一群更适合环境的个体,并经过数代的繁衍进化,最后收敛至一群最适应环境的群体,从而求得问题的最优解[12-13]。 遗传算法的主要运算过程如下。 (1)编码:在进行搜索之前将解空间的解数据表示成遗传空间的基因型串结构数据。对于多维、高精度要求的连续函数优化模型,可以采用浮点数编码方式。 (2)生成初始种群:初始种群规模的大小可以影响遗传算法的搜索质量和速度。大群体可以改进遗传算法的搜索质量,防止成熟前收敛。但是,大群体会增加个体适应性评价的计算量,从而降低算法收敛速度。随机生成M个个体,构成初始种群。M一般取值为20~200。 (3)适应度评价:基本遗传算法按照与个体适应度成正比的概率来决定当前群体中各个个体的生存机会,要求所有个体的适应度为非负数。费用函数可直接作为适应性函数。 (4)选择:选择是在群体中选择适应性强的个体产生新的群体的过程。遗传算法使用选择算子来对群体中的个体进行优胜劣汰操作。选择算子选用不当,会造成进化停滞或产生早熟现象。 (5)交叉:交叉是指对两个相互配对的染色体按照某种方式交换部分基因,从而形成两个新的个体。遗传算法的收敛性主要取决于交叉算子的收敛性。交叉概率Pc一般取0.4~0.99。 (6)变异:变异是指将个体染色体编码串中的某些基因座上的基因值用该基因座的其他等位基因来替换,从而形成新的个体。变异算子可以改善遗传算法的局部搜索能力,维持群体的多样性,防止早熟。变异概率Pm一般取0.001~0.1。 (7)终止条件判断:最常用的终止条件是规定算法的终止进化代数T,当算法迭代次数达到T时,停止运算,输出进化过程中所得到的具有最大适应度的个体作为最优解。T一般取100~500。 考虑由5个组成单元(U1~U5)构成的系统,要求系统故障检测率指标Psr不低于90%。各组成单元故障率、可达到的最高测试性水平、当前达到的测试性水平见表2,影响因素评分和影响因素权重评分分别见表3和表4。 表2 系统测试性数据 表3 影响因素评分 表4 影响因素权重评分 遗传算法参数设置:初始种群大小M=80,交叉概率Pc=0.8,变异概率为Pm=0.01,进化代数T=200。遗传算法运行结果见图5。由图可以看出,随着逐代进化,遗传算法收敛,能够优化得到最小费用。 图5 遗传算法运行结果 计算分配结果见表5。在进化到200代时,系统费用最低,其解可作为测试性指标的最终优化分配结果。 表5 分配结果 针对传统测试性分配方法在解决系统测试性指标优化分配方面的不足,引入了费用函数的优化分配模型。采用非线性费用函数,分析费用函数中各参数对费用的影响以及各参数的获取方法。针对费用函数最小化这一非线性规划问题, 采用遗传算法求解全局最优解。结果表明遗传算法能够获得合理的测试性分配值,费用函数可以用于系统测试性指标的优化分配。 [1] 田仲,石君友. 系统测试性设计分析与验证[M]. 北京:北京航空航天大学出版社,2003. [2] 刘刚,黎放,胡斌. 基于相关性模型的舰船装备测试性分析与建模[J]. 海军工程大学学报,2012,24(8):46-51. [3] 沈亲沐. 装备系统级测试性分配技术研究及应用[D]. 长沙:国防科技大学,2007. [4] 李金龙,陶凤和,贾长治,等. 基于AHP 的测试性分配方法研究[J]. 中国测试,2010,36(2):30-33. [5] 汤文超,李文海,罗恬颖. 基于D-S证据理论的测试性分配方法研究[J]. 中国测试,2016,42(4):111-114. [6] RAJESH J K,GUPTA S K,RANGAIAH G P. Multi-objective optimization of industrial hydrogen plants [J]. Chemical Engineering Science,2001,56(3):999-1010. [7] FULYA A,MITSUO G,LIN L. A genetic algorithm approach for multi-objective optimization of supply chain networks [J]. Computers and Industrial Engineering,2006,51(1):196-215. [8] 冉红亮,张琦,朱春生,等. 一种基于多目标优化的测试性分配方法[J]. 中国机械工程,2011,22(15):1775-1778. [9] 和麟,黄潇瑶,马存宝. 基于费用函数的航电系统可靠性优化分配方法[J]. 计算机与现代化,2012(10):1-4. [10] 邱静. 装备测试性建模与设计技术[M]. 北京:科学出版社,2012. [11] 刘飞,张为华. 基于费用函数的系统可靠性优化分配方法[J]. 机械设计与制造,2005(11):11-12. [12] 张延生,黄考利,陈建辉. 基于遗传算法的测试性优化分配方法[J]. 测试技术学报,2011,25(2):153-157. [13] 刘刚,黎放,胡斌. 基于改进遗传算法的测试性优化分配方法[J]. 火力与指挥控制,2014,39(1):44-47,57.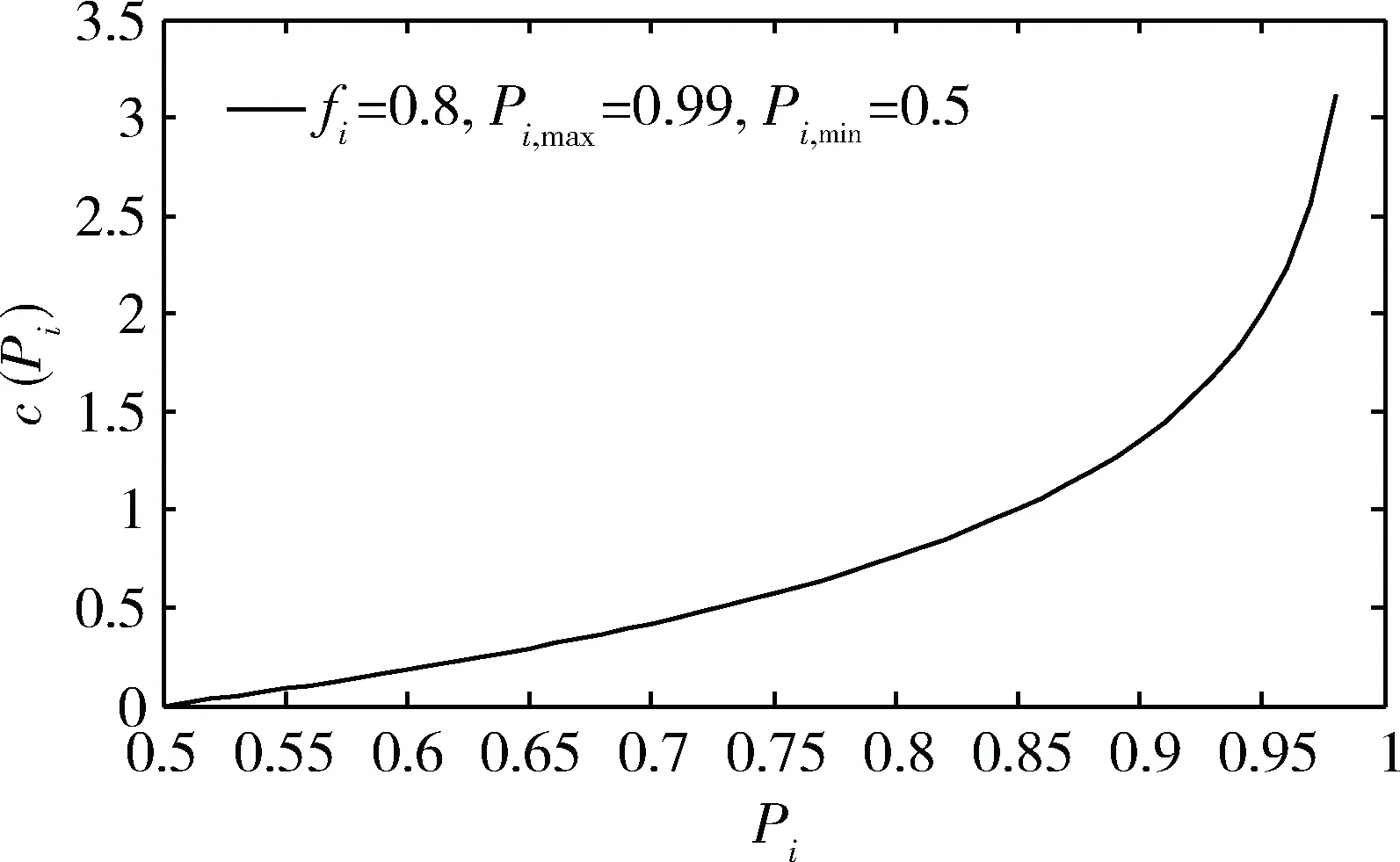
2.3 费用系数

2.4 可达到的最高测试性水平
2.5 当前达到的测试性水平

3 遗传算法
4 应用示例

5 结论
