基于非线性预处理和神经网络的字符序列单向Hash算法

朱 巍

(锐捷网络股份有限公司，福建 福州 350002)

0 引言

单向Hash函数在数字签名、身份认证、动态口令验证和完整性校验等领域中已经得到了相当广泛的应用。传统的单向Hash方法有MD5、SHA-1、RIPEMD-160和SHA-256等[1-2]，它们大多数基于复杂度的假设，需要进行大量的逻辑运算[3-4]，另外相关研究发现，这些算法已经并非足够安全[5-7]。

基于神经网络的Hash构造方法近些年来也引起了研究者的关注[8-12]。神经网络由于其内部复杂性、混沌性、扩散特性以及状态或者结构的时变性，已经被广泛地应用于数据保护和加密算法中，并且随着神经网络的单向特性(例如假设神经网络的输出层维数小于隐含层维数，那么可以很容易地通过输入得到输出值，却很难通过输出值逆向推导出输入)的不断深入研究，在密码学的单向Hash算法中，基于神经网络的方法也越来越多被提出。

然而目前大量基于神经网络的Hash方法并没有针对身份认证这一越来越广泛的使用场景进行优化，依然采用空白填充的方法将用户的密码序列进行对齐操作，这一步骤并不能增加信息的有效维度，并且加重了冗余计算，浪费了密码空间的复杂度[13-15]。另外，很多Hash方法中将原始字符序列的ASCII码直接输入到神经网络中，由于ASCII码中存在很多‘0’的二进制位[16]，并不能充分利用神经网络的输入权值，并不利于最终Hash码的鲁棒性。

本文提出了一种基于非线性预处理和递归神经网络(RNN)的字符序列的Hash构造方法，通过预先对字符序列进行非线性处理，得到字符序列的目标数值序列，并输入到RNN中，经RNN计算后得到最终的Hash值。通过理论分析和实验仿真，证明了本算法具有优秀的混沌扩散性质、抗碰撞能力以及单向特性，因此具有良好的理论研究价值以及现实应用意义。

1 Hash算法实现

1.1 非线性预处理

通过非线性预处理手段，可以将一维的字符序列映射到一个多维的混沌空间，有利于增强模型输入的复杂性，从而获得具有更加健壮的单向Hash函数构造模型。

设用户的字符序列X=[x1，x2,…，xN]T，其中N为序列的长度，序列中每个字符xi(1≤i≤N)均使用统一的字符编码集U进行二进制编码，例如ASCII编码、UTF-8编码等等。

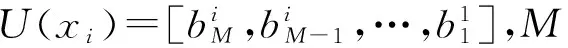
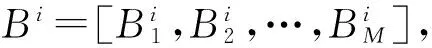
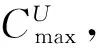
Ci=normalize(Di)

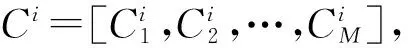
1.2 RNN的构建

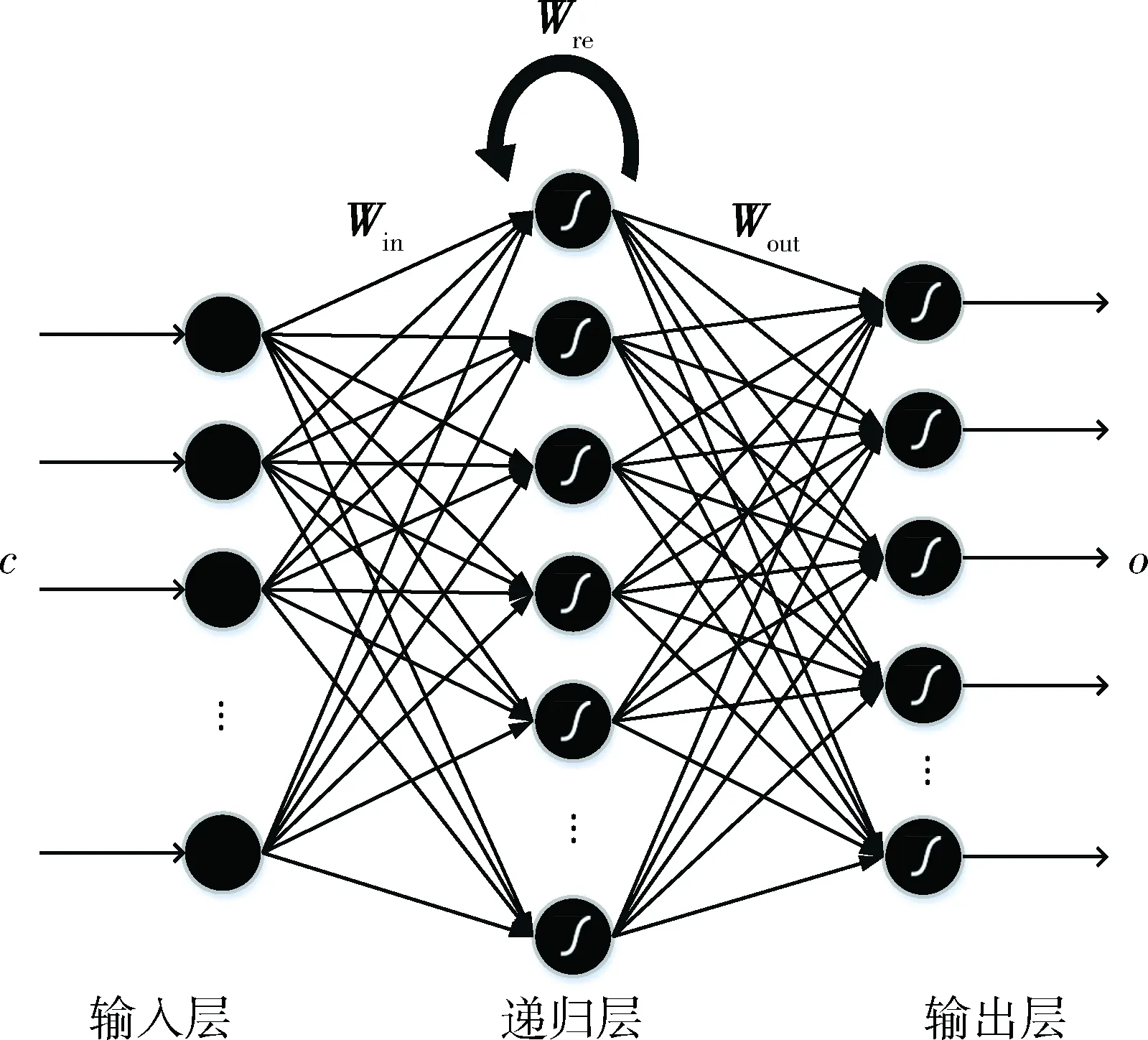
图1 网络模型

RNN结构如图1所示。其中输入层的节点数量为M(单个字符编码长度)，输出层的节点数量为期望得到的Hash码的长度的1/k(k为预设的Hash码增益长度系数)，记为L，中间递归层的节点数量记为P，且需要保证P>L。

对输入权值矩阵Win∈P×M、递归层反馈权值矩阵Wre∈P×P以及输出权值矩阵Wout∈L×P，递归层偏置值Bre∈P×1，输出层偏置值Bout∈L×1分别进行随机初始化。最后根据需要选定递归层和输出层的激活函数，例如sigmod、tanh函数。

初始情况下，RNNN的隐含层神经元状态为0，经过第一个输入c1后，状态为

S(1)=(Winc1+Bre)

(1)

从第二个输入c2到最后一个输入cN，隐含层神经元状态为

S(i)=(Winci+WreS(i-1)+Bre)

(2)

最终网络N的输出为

O(N)=(WoutS(N)+Bout)

(3)

1.3 Hash过程

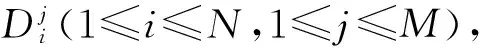
Hash的具体实施步骤如下：

(1)初始化递RNN，包括RNN的结构规模、权值初始化以及隐含层神经元状态置0。

(2)设置Hash码增益长度系数k，最终得到的Hash码长度将为k倍的RNN输出层维数，即kL。

(3)对密码字符序列进行非线性预处理，得到目标数值序列。

(4)将每个密码子夫的目标数值序列依次输入初始化好的RNN中，得到最终的网络输出O(N)。

(5)计算向量P=O(N)×10k，将P中每个元素值均转换成十六进制值，并取后位串联组成最终的Hash码。

2 实验

本文提出的算法采用MATLAB R2017a进行了实验仿真，并且取得了较好的实验效果，其相关代码可以从GitHub下载：https://github.com/JuiLangCHU/NP_ANN_HashAlgorithm。

这里假设有密码文本如下：

密码1：1b2FC1Pe6B94aZbD4740D7kd9L9B844f9g

密码2：2b2FC1Pe6B94aZbD4740D7kd9L9B844f9g

密码3：1b2FC1Pe6B94aZbD4840D7kd9L9B844f9g

密码4：1b2FC1Pe6B94aZbD4740D7kd9L9B844f9h

其中密码2与密码1仅首部第一个字符不同(1→2)，密码3与密码1仅中间第18个字符不同(7→8)，密码4与密码1仅尾部最后一个字符不同(g→h)。4组密码的Hash值如图2所示。

图2 4组密码序列的Hash值0、1序列图形

2.1 单向性分析

对于神经网络的最终输出向量O，由于从小数点后第二位开始取若干位作为Hash码，因此通过Hash值逆推网络输出的复杂度为o(24L)，L为神经网络的输出层维度，可见当网络输出层维数较大时，此步骤的计算复杂度相当高。

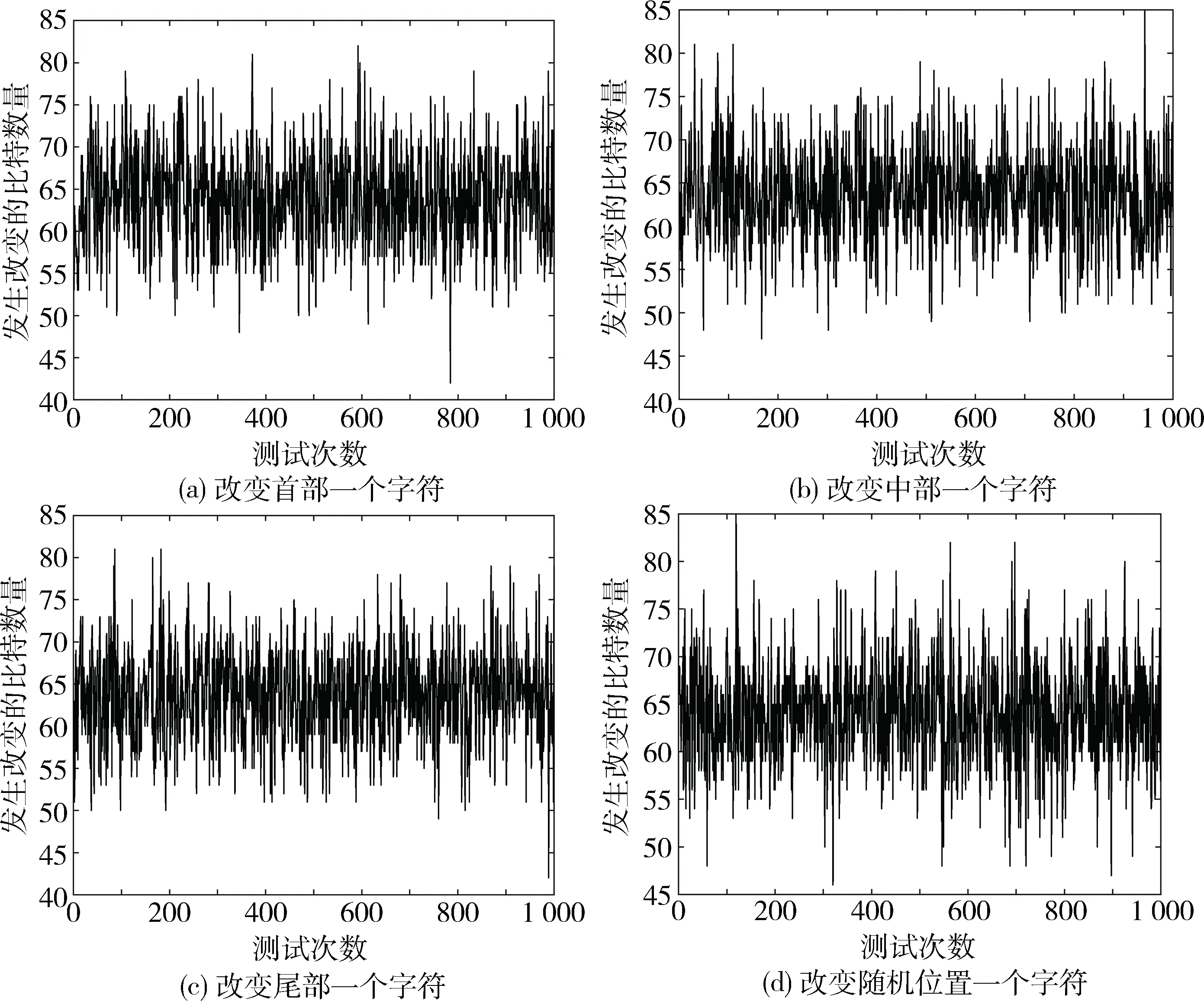
图4 改变密码序列不同位置的一个字符时，Hash码发生改变的比特数量(总Hash码长度为128)

另外，根据神经网络最终输出公式(3)得:

WoutS(N)=f-1(O)-Bout

(4)

其中，Wout∈L×P，S∈P×1，令φ=f-1(O)-Bout∈L×1，对公式(4)展开，可以得到：

⋮

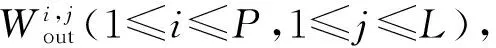
2.2 碰撞性分析

抗碰撞是指对于两个不同的原始输入序列，经过Hash算法后得到的Hash值相同的概率非常小。实验中，对于1个密码序列任意改变其中某一位置的一个字符，经过本算法得到128 bit的Hash码，并统计相同位置上对应的Hash值相同的次数，经仿真，统计结果分布如图3所示，超过18个字符相等的Hash码出现概率为0，说明算法具有良好的抗碰撞能力。

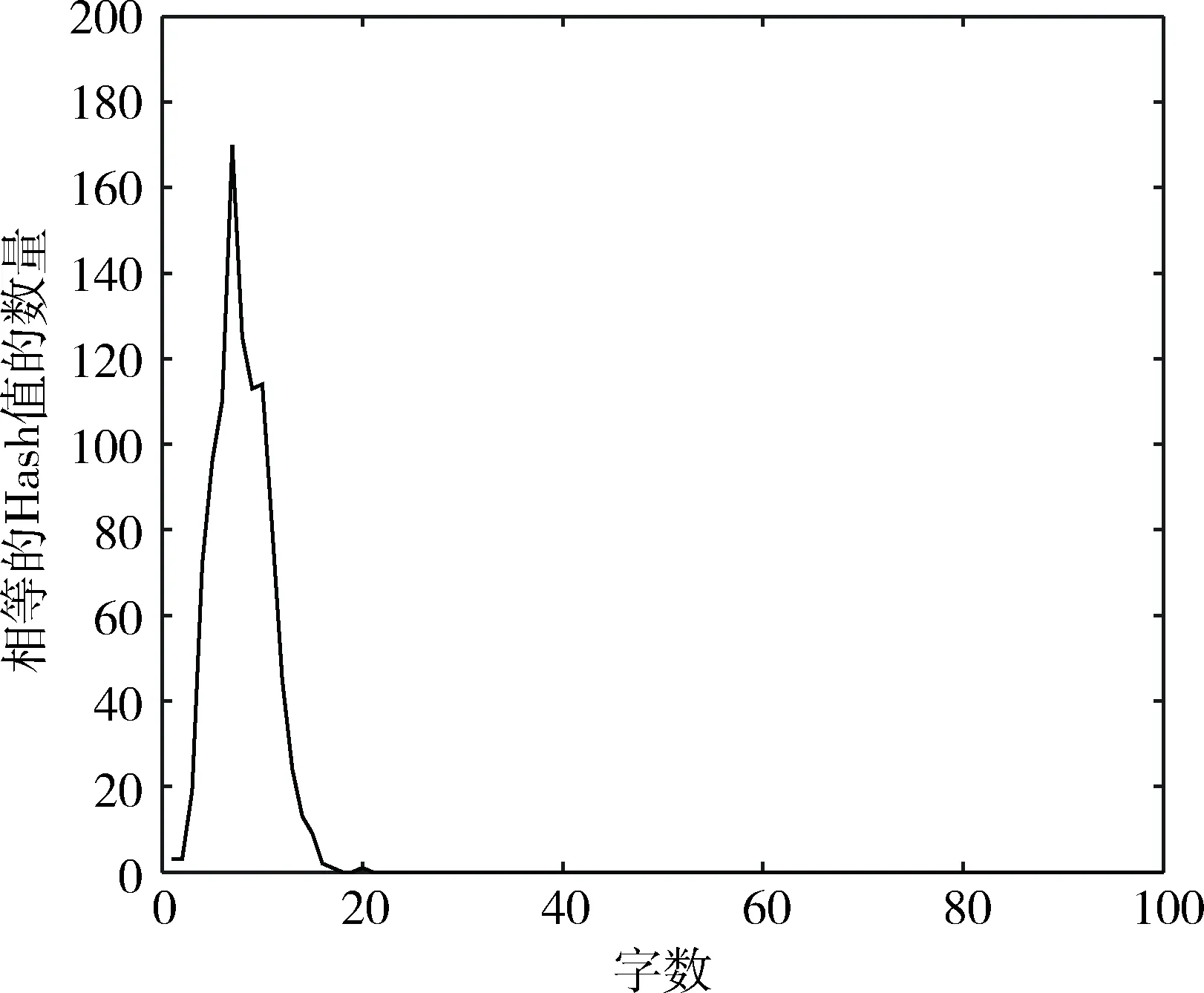
图3 相同位置具有相同Hash值的统计次数

2.3 扩散性和均衡性分析

随机取一段密码序列，并分别更改密码序列的首部、中部、尾部以及随机位置的一个字符，然后计算原始密码以及字符发生变化之后的Hash值，实验中Hash码的长度为128 bit。通过1 000次测试，计算得Hash码发生变化的比特数量分别为64.194、64.111、63.899、64.161，如图4所示。

由此可见，即使是不同位置的密码字符出现变化，对最终的Hash码的影响几乎是相同的，说明该Hash算法的平衡性非常均匀，并且最终Hash码的比特变化数量均非常接近Hash码总长度的50%，即64 bit，也说明了该Hash算法的混乱扩散性比较出色，能够敏锐地感知到原始密文序列出现的微小差异。

2.4 信息熵测试

为了度量一段消息中所含的信息容量，1948年由SHANNON C E提出了信息熵的概念，在信息论中，当熵最大时，信息量最大。对于Hash函数而言，熵最大时，Hash值的分布也越混乱，信息复杂度越高。熵的数学度量模型为：

且满足

0≤H(X)≤log|X|

其中|X|为取值个数。仅当变量X符合均匀分布时，H(X)=log|X|，即此时H(X)为最大熵。

为此，计算序列Hash码的信息熵，X为Hash码中不同字符的集合。

由于这里Hash码的取值为十六进制的0至F，理论上的熵最大值为log216=4 bit。对比以上4组密码序列的熵值(如表1所示)，可见已比较接近最大熵，表明其Hash码的混乱程度也趋近最大。

表格1 不同密码序列的信息熵值

3 结论

本文提出了一种基于非线性预处理和RNN相结合的密码文本序列Hash算法，其中非线性预处理可以显著地扩大递归神经网络输入层中不同字符的输入差异性，从而实现Hash构造函数对于微小差异的序列具有高敏感性。结合RNN中的参数敏感性、非线性等特点，可以实现安全地抗攻击的Hash构造方法，相关实验分析也证明了其有效性。此外由于RNN中的参数取值灵活，网络的规模也可以根据实际需要进行调整，因此在Hash实现中不需要对网络进行训练。综上所述，本文提出的算法具有高灵活性、易用性、扩展性和用户自定义配置性。

[1] RONALD L. RIVEST. The MD5 message-digest algorithm [R].MIT Laboratory for Computer Science and RSA Data Security, 1992.

[2] Federal information processing standards publication 180-1. secure hash standard [S]. 1995.

[3] Wang Shihong, Hu Gang. Coupled map lattice based hash function with collision resistance in single-iteration computation [J]. Information Sciences. 2012 Jul 15;195:266-76.

[4] WANG SHIHONG, LI DA, ZHOU HU. Collision analysis of a chaos-based hash function with both modification detection and localization capability [J]. Communications in Nonlinear Science and Numerical Simulation, 2012, 195(13):166-276.

[5] Wang Xiaoyun, Yao Fang. Crypt analysis of SHA-1 hash function [C].Proceedings of the 25th International Cryptology Conference, 2005:19-35.

[6] Xiao Di, Liao Xiaofeng, Wang Yong. Improcing the security of a parallel keyed hash function based on chaos map [J]. Physics Letter A, 2009:4346-4353.

[7] Yang Gang, Yi Junyan. Dynamics characteristic of a multiple chaotic neural network and its application[J]. Soft Computing, 2013:783-792.

[8] ABDOUN N, ASSAD S E, TAHA M A, et al. Secure Hash Algorithm based on Efficient Chaotic Neural Network [C]. 2016 International Conference on Communications. IEEE, 2016: 405-410.

[10] 陈军, 韦鹏程, 张伟, 等. 基于RBF神经网络和混沌映射的Hash函数构造 [J]. 计算机科学, 2006, 33(8):198-201.

[11] 李国刚, 钟超林, 蔺小梅. OHNN新的分组Hash算法 [J]. 华侨大学学报(自然科学版), 2015,36(4):393-398.

[12] XIAO D, LIAO X, WANG Y. Parallel keyed hash function construction based on chaotic neural network [J]. Neurocomputing, 2009, 72(10):2288-2296.

[13] LIAN S, SUN J, WANG Z. Secure hash function based on neural network [J]. Neurocomputing, 2006,69(16):2346-2350.

[14] HE B, LEI P, PU Q, et al. A method for designing hash function based on chaotic neural network [C]. International Workshop on Cloud Computing and Information Security (CCIS), 2013.

[15] LIAN S, LIU Z, REN Z, et al. Hash function based on chaotic neural networks [C]. Circuits and Systems, 2006.ISCAS 2006.IEEE, 2006: 4.

[16] URBANOVICH P, PLONKOWSKI M, CHURIKOV K. The appearance of conflict when using the chaos function for calculating the hash code [J]. Network, 2012, 88(11b): 346-347.