高速列车制动盘瞬态温度场分析

李 勇，祝汉燕，朱颖超

（1.中车长春轨道客车股份有限公司，长春 130062；2.中国平煤神马集团，平顶山 467000）

0 引言

制动技术是影响列车提速的重要因素。高速运行列车的制动装置或制动方式是确保列车安全运行的关键问题之一。当前世界高速旅客列车基础制动装置均采用盘形制动。某些国家在高速重载货物列车上也开始采用盘形制动，并对制动盘的材质、结构及制动闸片服役性能做了大量研究。

高速列车普遍采用摩擦盘形制动装置。随着列车运行速度的提高, 尤其是我国高速列车运营速度已经达到350km/h及以上，此时动能急剧增加，制动负荷载越来越来大，制动时产生的热能也大大增加。巨大的制动热负荷使制动盘产生很大热应力。由于热疲劳、高温蠕变、高温氧化及磨损等作用，大多制动盘已出现热疲劳裂纹。如果不加以控制，当扩展到一定程度后，可能导致整个制动盘断裂失效，直接影响着行车安全。因此高速列车在紧急制动时制动盘温度场的分布与制动盘的使用寿命密切相关。

1 能量输入模型

1.1 能量折算模型

从能量转换角度建立制动盘热输入模型[1,2]。由能量守恒定律可知，制动过程中的能量损耗（动能）转变为锻钢制动盘的输入热载荷（热能），并均匀施加在制动盘面上的接触摩擦区域。制动时，列车初速度为v0，某一时刻t时，车速变为vt，列车轴重为m ；由于制动过程热量转化为摩擦热能，取转化率为η则有下式：

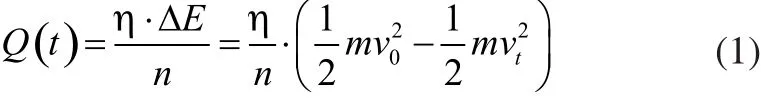
式中：n为轴闸片数。

假设热量在摩擦环上均匀分布。根据热流密度的定义，可以得到加载在每片制动盘摩擦面区域的热流密度与时间关系为：

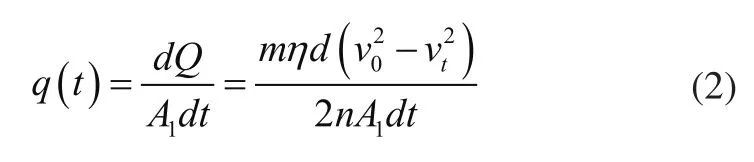
式中：A1为制动盘旋转一周闸片在制动盘摩擦面扫过的圆环面积。

1.2 摩擦功率模型

从摩擦功角度考虑制动盘的热输入[3,4]。对制动闸片摩擦半径径向方向进行环形微分，如图1所示。

以闸片距盘心r处的微分圆弧块作为研究对象[5]，则有：

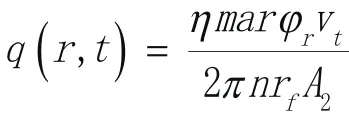
由上式可知，热流密度在制动盘径向位置的分布与

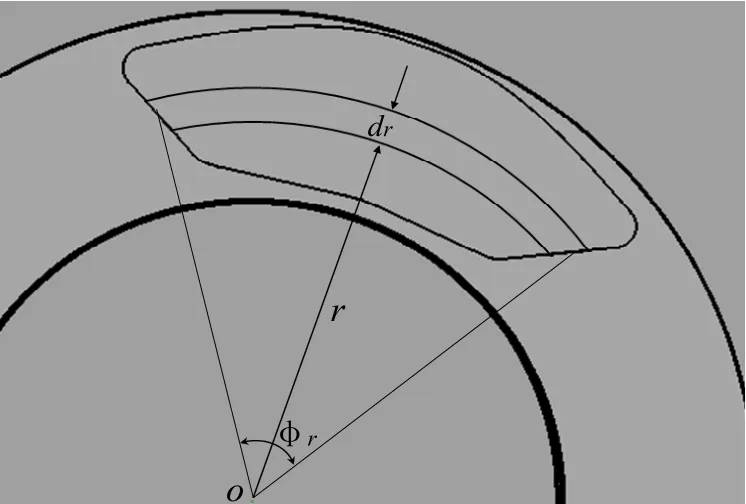
图1 摩擦面积计算原理

1.3 热流密度确定

1）列车匀减速制动

设列车运行方向为正，假定制动过程为匀减速，加速度为a，则制动过程任意时刻t的速度为可得热流密度随时间变化关系如下式：

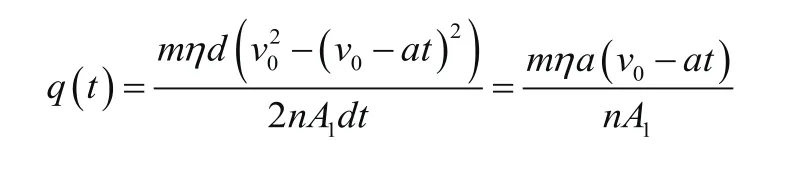
2）列车非匀速制动

初速385公里紧急制动，列车的制动速度如表1所示。

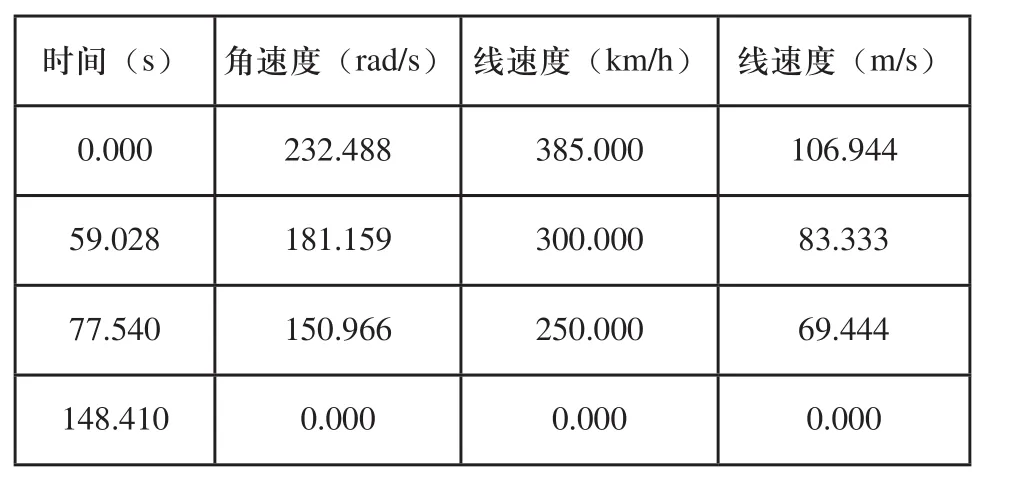
表1 速度385km/h时UB工况

轮半径r为0.46m，由线速度v=w.r可得列车速度。绘制线速度随时间变化关系曲线如图2所示。采用线性拟合，列车速度为vt=v0-at，其中a=0.7309，拟合度R2为0.9453。

采用二次多项式拟合，列车速度如下式：

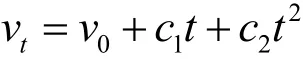
式中： c1=-0.2087，c2=-0.0035。

拟合度R2为0.9999，结果更好。研究中采用二次曲线表达列车制动过程中的速度变化以及热流密度变化。

于是可得热流密度随时间变化关系如下式：

式中：v0、c1和c2为与速度有关的常数；

A1为摩擦面积。

通过速度的线性和二次曲线拟合得到随时间变化的热流密度q(t)，如图3所示。

由图3可知，采用线性拟合速度得到的热流密度随时间是线性递减过程；而采用二次多项式拟合得到的热流密度则是随时间先增大后减少。这主要是因为制动时热能快速累积至一定程度，制动盘温度急剧上升达到峰值，随后在热对流和辐射作用下热流密度将逐渐降低，与实际情况相符。

2 热损失边界

在动车制动及停车过程中，制动盘内存储的巨大能量会散到空气中。制动过程为强迫对流，停车后为自然换热，必须考虑随列车行进速度变化的热量损失。

2.1 热对流模型

在制动过程中盘体对流散热时，空气流动的Rem数[6,7]：

式中：v为空气来流速度；

L为盘的特征长度，取该点所在位置的圆周周长；

υ为空气运动粘滞系数。

混合边界层平均对流传热系数：

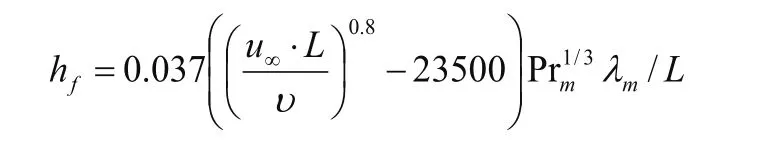
式中：Prm为普朗特常数；

λm为空气导热系数。

2.2 热辐射模型

Newton定律和Stefan-Boltzmann方程，将热辐射折算成换热系数为：

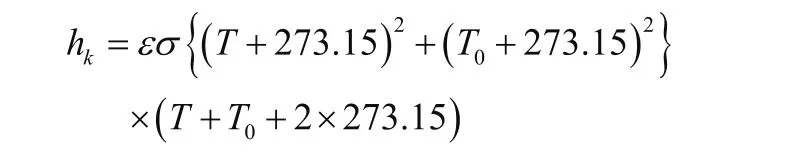
式中：ε为辐射率；

σ为斯蒂芬-玻尔兹曼常数。

2.3 综合换热系数

制动盘表面换热系数由表面与环境的对流换热和辐射换热两部分组成[4]，即：

由对流换热系数与辐射换热系数累加得到表面综合换热系数，其随温度变化曲线，如图4所示。这里，对流换热系数随时间逐渐减少，取制动中间时刻的对流换热系数来换算表面综合换热系数。

图4 制动盘表面综合换热系数变化

3 仿真计算分析

3.1 制动盘分析模型

将建立的制动盘三维模型，然后导入ABAQUS软件中，考虑到几何结构的对称性，以及方便在热应力分析中加对称约束，取四分之一作为有限元输入几何模型，如图5所示。

图5 制动盘模型

分析选用线性四面体单元，设置网格整体尺寸为0.006m，模型包含19166个节点和90289个单元，图6为制动盘1/4有限元模型图。

图6 制动盘1/4有限元模型

3.2 锻钢制动盘材料物理特性

高速列车在制动过程是一个摩擦过程，摩擦产生的热使制动盘温度急剧上升，引起了制动盘材料在制动过程中其物理特性变现为非线性，如图7所示为材料的弹性模量、线性膨胀系数、导热系数、比热容随温度的变化曲线。

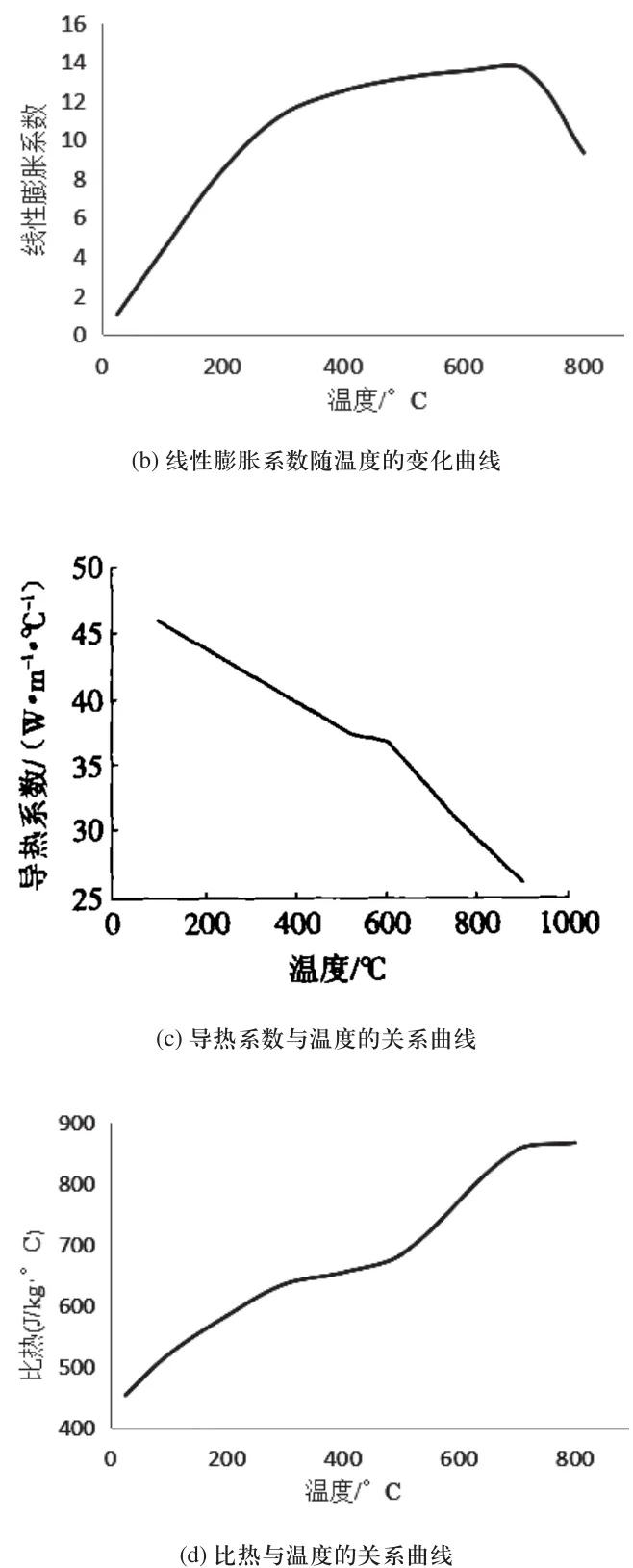
图7 材料参数随温度变化曲线

3.3 边界条件设置

温度约束设置，环境温度设置为25℃，根据前面分析得到表面综合换热对流系数，热输入载荷设置中，采用能量折算和摩擦功率模型以及匀减速或者变减速得到不同情况下的热流密度变化，如图8所示。

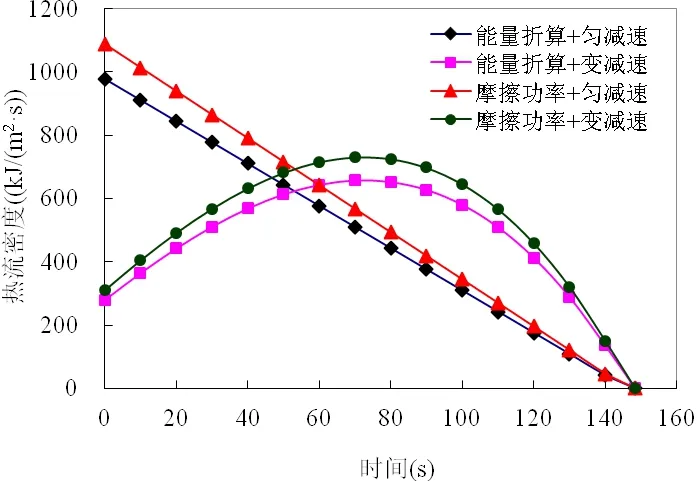
图8 载荷输入数据热流密度

由图8可知，列车均减速时制动盘累积的热量能够得到及时的释放，而在变减速时，由列车动能转化的巨大热能来不及散发至空气中，因此使得制动盘温度迅速升高，这是影响制动盘寿命的重要工况。

3.4 仿真计算结果分析

以初速度385公里紧急制动计算得到制动过程节点号7593（如图9所示）对应的温度变化曲线图10所示。计算中考虑了能量折算和摩擦功率以及采用匀减速和变减速的四种不同组合。

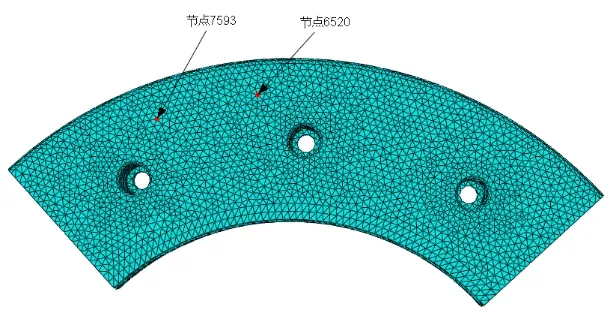
图9 节点号7593在模型中位置

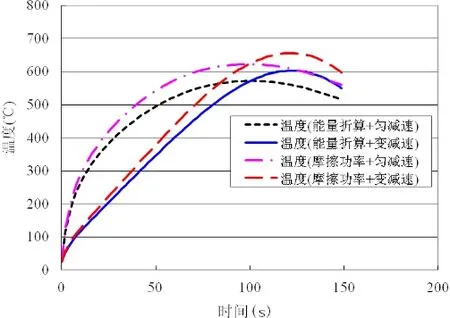
图10 节点7593对应的温度变化曲线

由图10可知，变减速条件下无论是采用能量折算法还是摩擦功率法，制动过程的最高温度约为600℃，这与实验检测结果基本一致。

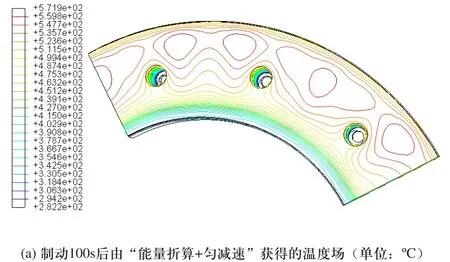
针对匀减速和变减速两种工况，采用不同的能量计算方法的组合，取最高温度时刻的温度场绘制等高线图，如图11所示。

【】【】

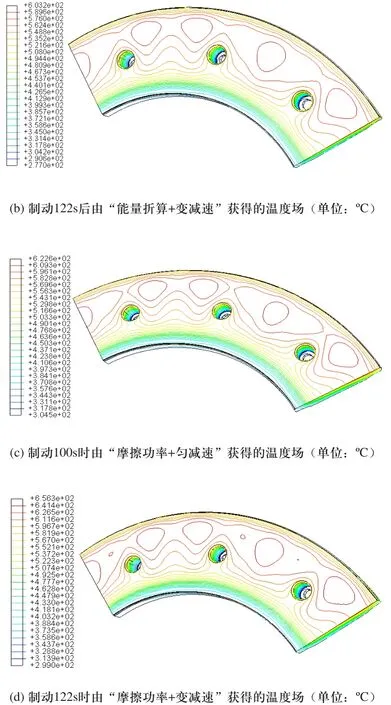
图11 温度场等高线图

由图11可知，四种模型对应最大瞬态温度从高到低依次是：摩擦功率+变减速、摩擦功率+匀减速、能量折算+变减速、能量折算+匀减速。最大瞬态温度总是出现在摩擦面中央到外径侧处。从以上四种能量计算方法获得的峰值温度场分布可以看到，不同制动盘热输入模型热分析得到的最大瞬时温度区域皆位于散热孔的中间靠上部的微小局部区域，并不是均匀分布。据此可以推测，该局部微小区域的热应力亦将表现出较大的梯度变化，从而容易引起热疲劳裂纹。

4 结论

1）研究表明，由于考虑了摩擦副周向接触长度对接触面摩擦生热热流密度分布的影响，所得的摩擦面中央到外径侧处的盘体温度要高于能量折算法的计算值，而盘体内侧的温度则低于能量折算法的计算值。

2）研究中采用摩擦半径rf为0.305m时的热流密度整个加到摩擦环上，并提取最高温度点（在中央到外径之间）温度，从而得到“摩擦功率”模型的最大瞬时温度普遍高于“能量折算”模型。但真正是否“摩擦功率”法获得的结果是否偏危险还要重点考察由各工况下的瞬时温度场引起的热应力场以及缺陷所在位置、方位和尺寸等因素的影响。

3）制动盘最大瞬时温度区域皆位于散热孔的中间靠上部的微小局部区域，并不是均匀分布。据此可以推测，该局部微小区域的热应力亦将表现出较大的梯度变化，从而容易引起热疲劳裂纹。

[1]张新芳.160km/h货车制动盘热-应力及强度分析[D].成都:西南交通大学,2012.

[2]李继山.高速列车合金锻钢制动盘寿命评估研究[D].北京:铁道科学研究院,2006.

[3]杨强.列车制动盘温度场和应力场仿真与分析[D].北京:北京交通大学,2009.

[4]张乐乐,杨强,谭南林,李卫京.基于摩擦功率法的列车制动盘瞬态温度场分析[J].中国铁道科学,2010,31(1):99-104.

[5]孙新海.盘形制动及其配套技术[M].北京:中国铁道科学,1998.

[6]罗继华,杨美传.动车组拖车制动盘有限元热分析[J].铁道车辆,2009,47(4):22-25,48.

[7]曹玉璋.传热学[M].北京:北京航空航天大学出版社,2001.