变式数学真奇妙，颠来倒去皆可照——暨观摩公开课《15.4角的平分线》后的一点感想

安徽省宣城市绩溪县适之中学 吕国梅

近期有幸观摩市骨干教师张晓峰的公开课——《15.4角的平分线（习题课）》。随着教学年份的增长，我越来越感到教学的茫然和无所适从，在教育方面层出不穷的新问题曾一度让我对教学产生倦怠、困惑、迷茫，站在轰轰烈烈新课改的浪潮中，我被一波又一波的巨浪席卷致晕眩——教育未来的模式到底是什么样的？尤其是对我们初中数学课堂而言，又有什么样独特的教育方式能够改变？学生头脑中根深蒂固，现实中又是真真切切的令人觉得枯燥无味，更为关键的是被众多人认为 “百无一用是数学”，更何况是初中数学。二十多年的初中数学教学生涯以及那点所谓的教学经验，说得直白一些就是残酷的教学现实——理想很丰满，现实很骨感。想成为一名成功的好老师那，可不是一件容易的事，所以才有这样到处求学的需求。

张老师的课成功之处首先在于他敢于挑战这种我们大多数老师都认为最难 “表演”的习题课——15.4角的平分线（习题课）。角的平分线从性质定理到判定定理都有非常充实的内容可讲，可我们的张老师偏偏选择了习题课。最为关键的也是这节课最大的亮点就是张老师选了一个变式练习作为这节课的主基调，最大程度地凸显了数学的奥妙与神奇——万变不离其宗，数学知识之间存在着某种内在的、相互转换的联系。变式练习平时我也操作，但像张老师这样利用一节公开课的时间和大家共同探究、研学，我还是有些顾忌的。最后让所有老师啧啧称赞的是张老师那精湛绝伦的高超的多媒体使用技术，让我们后面这些对几何画板一窍不通的老师看得目瞪口呆。

下面我把张老师这节课的大致环节和成功亮点用我的拙笔记录下来与大家共同分享。首先张老师按照常规教学复习回顾了角平分线的性质定理和判定定理。

张老师在多媒体上用几何画板呈现图1，并和同学们一起简要温习整个定理的推导过程，学生集体口头叙述，张老师在黑板左侧整齐规范地板书证明过程。

性质定理：∵∠1=∠2，PD⊥OA，PE⊥OB，

∴PD=PE。

判定定理：∵PD⊥OA，PE⊥OB，PD=PE，

∴∠1=∠2。

一、解题过程中的几大亮点

（1）复习导入式常规教学非常符合学生的认知规律，也正体现了知识的积累与循序渐进的习得过程。学生在这一环节表现出了极高的热情与参与程度，由此也正恰恰能够体现张老师平时的课堂教学深受学生喜爱的程度。

（2）张老师在板书时兼顾了大多数同学的表述，对于表述有错误瑕疵的地方，老师都做了详细的解说，再次更正了同学们的错误理解。对于上一节课的知识也是最好的巩固和提高方式。

（3）这大概是这个环节最吸引大家眼球的地方，当张老师动态演示P点的位置时，性质定理显示动画PD=PE并且等于某个具体的长度，当改变点P的位置 ，PD与PE的长度也会随之发生改变，但始终保持PD=PE这个结论不变。判定定理中同样利用几何画板动态演示改变P点的位置，可见∠1=∠2这个结论，并且同样用表格的形式呈现这个等量关系。随着点P的运动，∠1、∠2的度数也会随之发生改变，但∠1=∠2这个结论始终保持不变。

二、习题的变式应用

接下来便是这节课的正题，同一道题，张老师通过一题多解、交换题目条件与结论构成互逆命题、稍微改动题目的条件和结论衍生出若干个系列题系，也正是借助这种题目的讲解对学生进行知识系统化。

例1 如图2所示，已知OP是∠AOB的角平分线，OA＜OB,PA=PB，求证：∠OAP+∠B=180°。

方法一：过点P分别作PD⊥OA,PE⊥OB于点D、E，

∵OP是∠AOB的角平分线，

∴PD=PE，

∵PA=PB，

∴△PAD≌△PBE（HL）。

∴∠B=∠PAD，

∵∠OAP+∠PAD=180°，

∴∠OAP+∠B=180°。

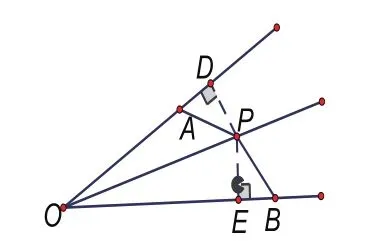
图2

方法二：如图3，在OB上截取OC=OA，

∵OP是∠AOB的角平分线，

∴△OAP≌△OCP（SAS）。

∴∠OAP=∠2，∴PA=PC，

∵PA=PB，

∴PC=PB，

∴∠1=∠B，

∵∠2+∠1=180°，

∴∠OAP+∠B=180°。

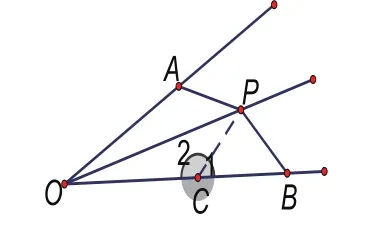
图3

变式1：（交换题目条件与结论，形成互逆命题）如图4所示，已知OP是∠AOB的角平分线，OA＜OB,∠OAP+∠B=180°，求证：PA=PB。

证明：过点P分别作PD⊥OA,PE⊥OB于点D、E，

∵OP是∠AOB的角平分线，

∴PD=PE，

∵∠OAP+∠B=180°，

又∵∠OAP+∠PAD=180°，

∴∠PAD=∠B，

∴△PAD≌△PBE（AAS），

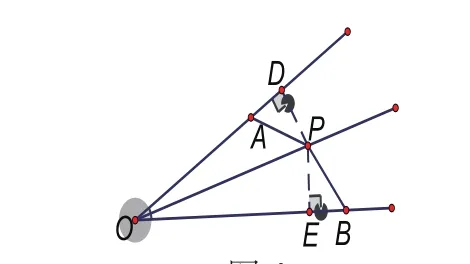
图4

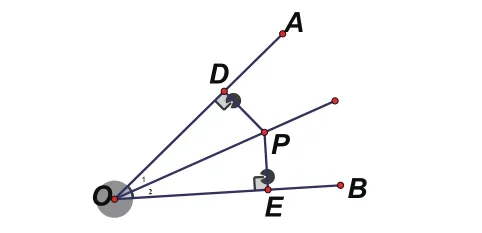
图1

∴PA=PB。

变式2：（题目条件不变，结论改变）如图5所示，已知OP是∠AOB的角平分线，OA＜OB,PA=PB，求证：OA+OB=2OE。

证明：过点P分别作PD⊥OA,PE⊥OB于点D、E，

∵OP是∠AOB的角平分线，

∴PD=PE，

∴△PAD≌△PBE，△POD≌ΔPOE（HL），

∴AD=BE，OD=OE，

∴OA+OB=（OD-AD）+（OE+BE）=OE-BE+OE+BE=2OE。

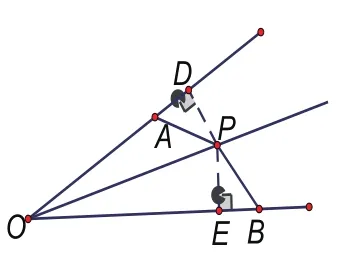
图5

三、变式训练在数学教学中的思考

教学活动是教师的教与学生的学的“双向”活动。授之以鱼不如授之以渔，教学的目的不在于“鱼”而在“渔”，数学习题教学更应如此。习题作为课本的有机组成部分之一，蕴涵着丰富的内涵和背景，教学中若能充分挖掘课本习题的潜在功能，像张老师这样进行一题多解和一题多变，定会收到事半功倍的教学效果。数学习题教学的目的是使学生牢固掌握数学知识，提高学生的数学能力。

总之，在数学教学过程中可以根据不同情况采取变条件、变结论、变形式、变图式等方法，使学生对所学的知识进行分析、综合、归纳、整理，使之系统化、深刻化，掌握各部分知识之间的内在联系，提高自己的思维能力。而变式训练同样是帮助学生提出问题、分析问题、解决问题。从一题多解、一题多变、多题一解、一题多图、多图一解等多角度进行变式训练。通过种种训练引导学生多侧面、多角度、多渠道地思考问题，让学生多探讨、多争论，能有效地训练学生思维的完备性、深刻性和创造性，大大激发了学生的兴趣，从而培养了学生的创新能力。