探究三元函数最值的求解策略

江苏省盱眙中学高三（21）班 叶泞珲

最值问题是高中数学学习的重点和热点问题，处理多变量函数的最值问题通常需要减元。在高三复习中发现，近几年在高考中经常出现三元函数(含有三个变元的函数)的最值问题，而且难度较大，同学们对这类问题感觉比较棘手，本人对此问题做了一些探究，以几例分析求解策略如下，仅供参考。

一、代入减元

解后反思：当给出三元条件等式求一个三元函数的最值时，通常将三元条件等式中的两个变元用另外一个变元表示代入减元，转化为二元函数求最值问题。

二、重组变元

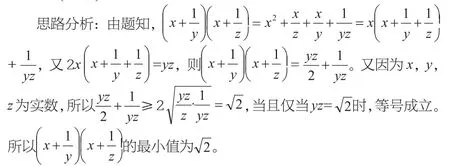
解后反思：初看这是一个三元式的最值问题，无法直接利用基本不等式来解决。换个思路，可考虑将展开重新组合，变于是就可以利用二元基本不等式求解了。

三、“1”的代换

例3.（2013苏南四校12月检测）设正实数x，y，z满足

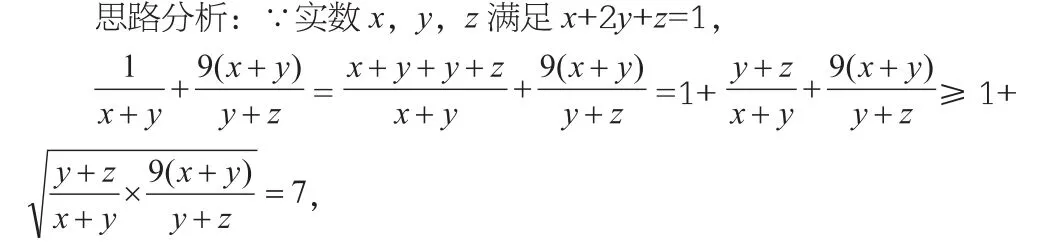
解后反思：本题直接用条件等式x+2y+z=1，将三元函数中的“1”换成条件等式的左边，然后分离，把“x+y”和“y+z”当作整体，转化为二元函数求最值问题。

四、并元处理

思路分析：根据题意可得f '（x）=ax2+bx+c≥0在R上恒成立，则a＞0，Δ=b2-4ac≤0。

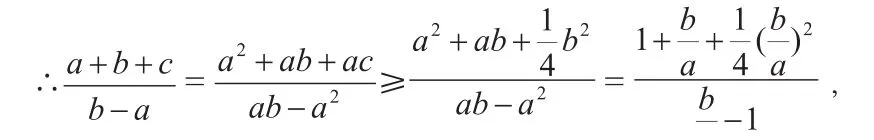
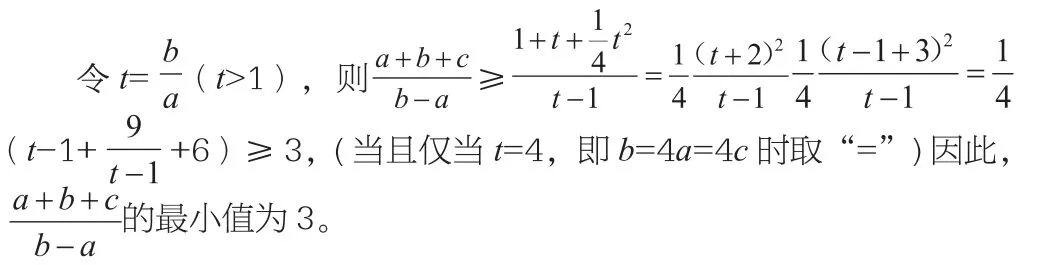
五、数形结合

例5.已知实数a，b，c满足a2+b2=c2，c≠0，则的取值范围为_____ 。

解后反思：本题考查了三角函数换元法、直线的斜率计算公式、直线与圆的位置关系、点到直线的距离公式，考查了数形结合及转化思想，考查了推理能力与计算能力。

六、两次变形

例6.(2017无锡期末）已知a＞0，b＞0，c＞2，且a+b＝2，则的最小值为 。

思路分析：根据目标式的特征，进行恰当的变形，利用基本不等式知识求解。

解后反思：本题的关键是首先通过固定变量c(视a，b为主元)，然后利用代换(齐次化)、配凑等技巧对代数式进行两次变形使用二元基本不等式，并结合不等式的性质巧妙地求得了最小值。

七、逐步消元

例7.已知x，y，z∈R，且x+y+z=1，x2+y2+z2=3，令xyz的最大值是_______。

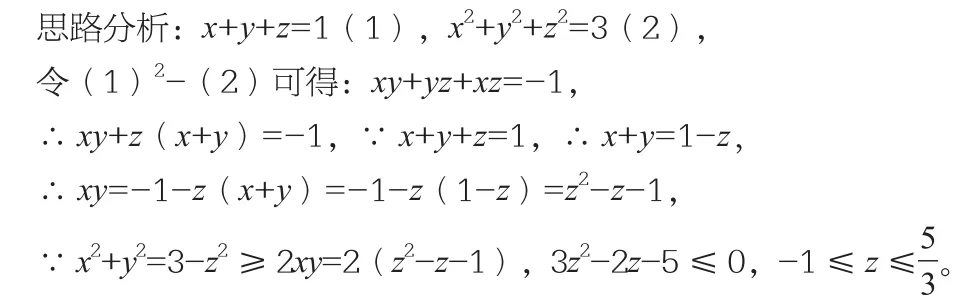
令 f（x）=xyz=z3-z2-z，则 f'（x）=3z2-2z-1=（z-1）（3z+1），

解后反思：由条件可得xy+yz+xz=-1，利用x+y+z=1，逐步消元可得xyz=z3-z2-z，利用导数的方法，可求出xyz的最大值。

八、各个击破

例8.（2017泰兴中学）已知x，y，z均为非负数且x+y+z=2，则的最小值为 。

思路分析：∵x≥0，y≥0，z≥0，且x+y+z=2，∴z=2-x-y≥0，即x+y≤2。令函数则 f′ (x)=x2-1， 当 x∈ (0，1)时，f′(x)＜0，∴f(x)在(0，1)上单调递减；当x∈(1，2)时，f′(x)＞0，∴f(x)在(1，2)上单调递增，∴f(x)min=f(1)。同理：令g(y)=y2-y，则g′(y)=2y-1，当时，g′ (y)＜0，∴ g(y)在上单调递减；当时，g′(y)＞0，∴g(y)在上单调递增，

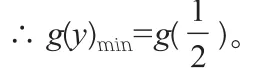
解后反思：本题求解不知道如何下手，但是容易想到将z=2-x-y代入化为二元问题，突破口是分别把x，y当作主元，得到个一元函数分别利用导函数研究单调性，求其最小值即可。