页岩压裂裂缝渗透率的测试与分析

尹 丛 彬

中国石油天然气集团有限公司川庆钻探工程公司井下作业公司

0 引言

页岩储层的基质渗透率极低，通常作为有效储层的盖层，其天然裂缝/层理缝发育，一定程度上改善了局部渗透率[1-4]，但仍无法满足页岩气开采所需的有效流动通道需求。为实现商业开采，需要水力压裂形成大规模的裂缝网络，即体积压裂[5-8]。目前，体积压裂的增产机理尚不明确，如压后形成的大量闭合裂缝、剪切微裂缝、充填裂缝对渗透率的贡献以及各种措施对这些微裂缝渗透率的影响等[9]。体积压裂的成功很大程度上是基于油田现场的经验。需要通过设计一系列的实验来研究这些影响因素，提高体积压裂的有效性。

先前一些研究描述过裂缝渗透率的特点。Kranzz等[10]研究过有效应力、粗糙度对花岗岩裂缝渗透率的影响，发现裂隙岩体相比全岩来说对压力更敏感，认为裂缝表面的平板模型是不充分的。Tsang和Witherspoon的模型[11]认为，裂缝的不匹配减小了应力—裂缝闭合行为的非线性特征；他们还认识到粗糙度的重要性，注意到当存在大尺寸波状面时，在剪切位移超过1/2个大波长后，流量随着剪切位移的增大而降低。Gangi[12]认为，一个裂缝和它对压差的依赖性可用“二度梳状函数模型”更好地反映出来。笔者选择用Walsh模型[13]解释裂缝渗透率与压力的关系，因为该模型是连接渗透率和围压的最简单模型。

裂缝导流能力和支撑剂充填渗透率的影响因素研究也有文献报道。在无支撑剂充填情况下，诸如裂缝错位、裂缝粗糙度、岩石力学性质和闭合压力对导流能力的影响已经被研究[14-16]。当出现支撑剂时，注入支撑剂强度、浓度和闭合压力这些参数展示了重要性[17-18]。然而，这些研究都是用平板岩心开展的。Fredd等[9]利用劈裂的砂岩，研究了低铺砂浓度下，裂缝性质对导流能力的影响，探讨了支撑剂和粗糙度对导流能力的作用效果；但对于不同的页岩，剪切错位与渗透率的关系、支撑剂的铺置等影响都没有研究。

以四川盆地下寒武统鲁家坪组、上奥陶统五峰组、下志留统龙马溪组和上三叠统须家河组页岩为研究对象，综合应用裂缝渗透率测试与CT扫描手段，系统研究了页岩裂缝类型（原位闭合型、剪切自支撑型、单层支撑型）、裂缝面粗糙度、碳酸盐矿物含量、页岩层理、围压等因素对裂缝渗透率的影响，以期为页岩压裂工艺优选、参数优化提供指导。

1 不同层组页岩的特征

1.1 矿物组成及特征

为研究页岩矿物组成、天然裂缝/层理缝对裂缝渗透率的影响，以四川盆地鲁家坪组、五峰组、龙马溪组和须家河组页岩为研究对象，各层组取8块页岩岩样，包括平行层理4块和垂直层理4块（图1），对每组岩样进行岩石组成矿物分析，得到结果如下：①鲁家坪组。黏土含量为22.5%，碳酸盐含量为25%，石英含量为40.5%。②五峰组。黏土含量为14.5%，碳酸盐含量为2%，石英含量为68.1%。③龙马溪组。黏土含量为31%，碳酸盐含量为15%，石英含量为43.3%。④须家河组。黏土含量为40.6%，碳酸盐含量为10%，石英含量为44.3%。岩心外观观测发现：五峰组、龙马溪组页岩层理缝，高角度天然裂缝较发育；鲁家坪组、须家河组页岩裂缝欠发育。对每组岩样采用劈裂的方式得到不同人造裂缝类型（原位闭合型、剪切自支撑型、单层支撑型），以实现不同裂缝渗透率测试与评价。

图1 典型层组页岩岩心图

1.2 微观孔隙及裂缝特征

对4个层组岩样外观观察分析发现：五峰组和龙马溪组均有天然裂缝，而且是贯穿整个岩样的，而鲁家坪组岩样仅有1条非贯穿的有白色胶结物质的裂缝。借助CT扫描进行岩心裂缝及孔隙分析表明（图2）：五峰组和龙马溪组岩样均有贯穿的连通裂缝，其余基质部分十分致密，难以观察到大的孔喉。鲁家坪组2 mm小岩心纳米CT扫描（绿色部分代表基质，红色部分代表孔隙）结果显示：该岩心仅有少量分散的孔隙存在，其余为致密的基质，只有在非贯穿裂缝的裂缝面上有较多的非连通孔隙。

1.3 裂缝壁面粗糙度

采用三维激光扫描仪对岩样进行扫描，基于扫描数据，利用Surfer软件绘制裂缝表面形貌图（图3）。岩石裂缝壁面粗糙度可由表面分形维数（以下简称分维数）表征[19]，采用立方体覆盖法计算出了16组岩心裂缝壁面的分维数[20-22]。结果表明：岩心裂缝面形貌各异，壁面粗糙度可用分维数来定量描述，分维数越大，壁面粗糙度越大，4组岩样的分维数范围为2.035 1～2.109 1。将每组岩样平行层理和垂直层理的分维数分别取平均值，绘制分维数与碳酸盐矿物含量的关系图（图4）。从图3可以看出：①每组岩心内（矿物含量相近），与层理垂直的裂缝面粗糙度大于平行于层理的裂缝面粗糙度；②裂缝面分维数基本随碳酸盐岩含量的增加而增大，主要是因为碳酸盐矿物颗粒晶体的尺寸相对较大，且圆球度较低，当含量增加时，局部集中胶结可能导致裂缝壁面粗糙度更大。

2 页岩压裂裂缝渗透率测试

2.1 原位闭合型裂缝渗透率

断裂后裂缝面原位对准，且没有任何充填称为原位闭合型裂缝，参考威远浅层目标井区储层埋深为1 525 m左右，最小水平主应力为29 MPa左右，生产初期气水同产阶段井底压力为12～14 MPa，生产后期产气阶段井底压力为9～10 MPa，不同生产阶段作用在支撑剂上的有效闭合应力为17～20 MPa，因此，对上述页岩样品在3～20 MPa的围压范围内进行渗透率的测试，实验结果如图5所示，所测32组岩样原位闭合型裂缝渗透率范围为0.15～16.75 mD，各组岩样原位闭合型裂缝渗透率规律如下所述。

2.1.1 五峰组

各组岩样渗透率差别较大，最大的差距是在3 MPa围压下，相差幅度达8.40 mD，随着围压的增大，各组渗透率的差值逐渐减小。渗透率受围压影响的敏感性有较大差异，最大变化幅度为94.92%，最小变化幅度为60.78%，其中，平行层理1和垂直层理3的渗透率随围压变化很小，主要是因为该两组岩心被劈裂后，裂缝面没有受到太大的伤害，导致其裂缝的原位闭合渗透在小围压下就维持在较低的水平。

图2 页岩岩样CT扫描结果图

图3 裂缝表面形貌图

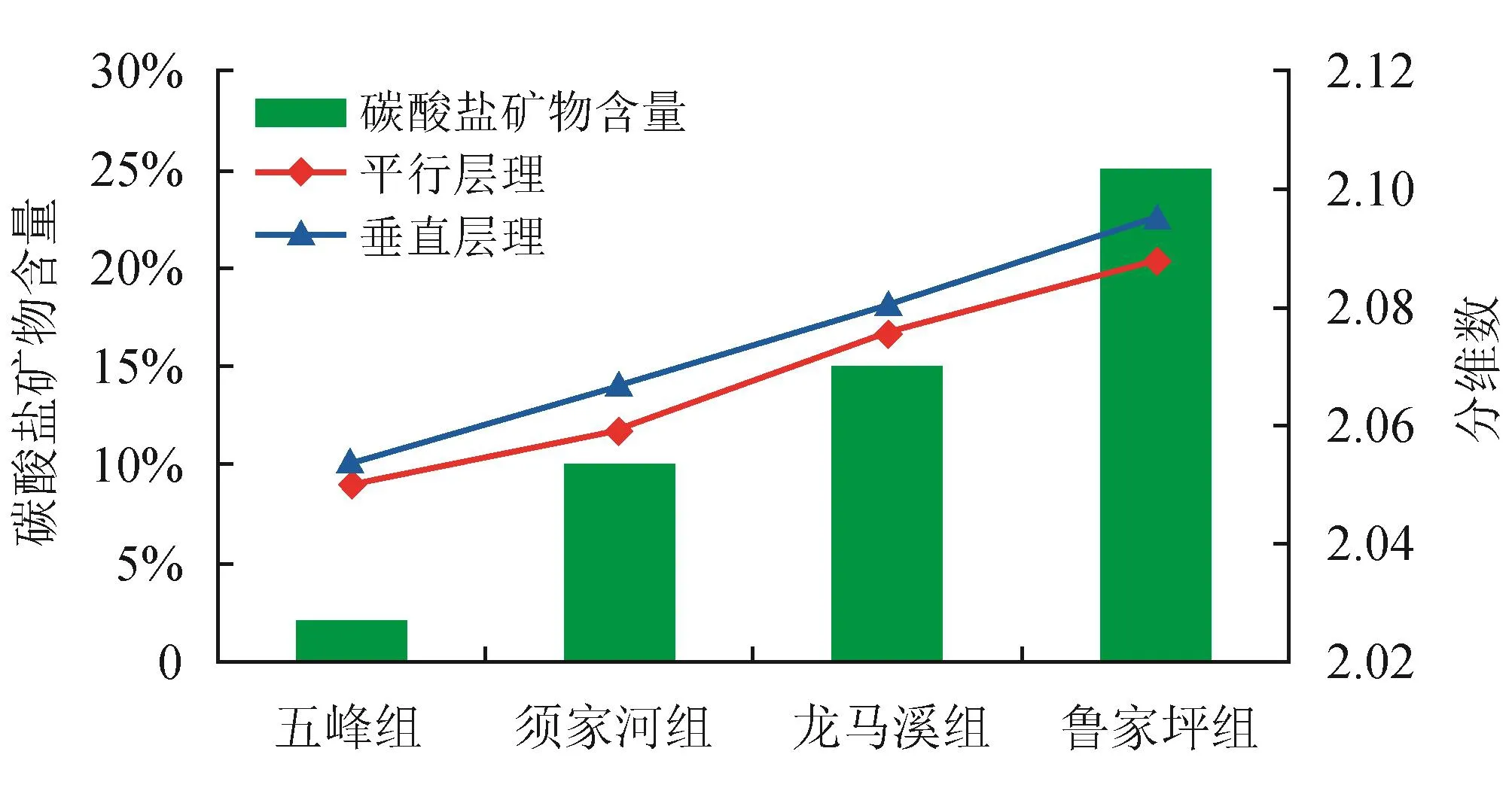
图4 裂缝壁面分维数与碳酸盐矿物含量、层理关系图

2.1.2 须家河组

各组岩心渗透率随围压变化的趋势较为一致，在3 MPa下，组内渗透率差距很大，变化幅度高达13.7 mD，随着围压的增加，在每一围压下组内的渗透率差距迅速减小，在20 MPa围压下，渗透率集中在0.20～0.44 mD，组内差距很小。

2.1.3 龙马溪组

各组渗透率在各个压力点均表现出较大的差距，最大相差15.72 mD。岩样渗透率随围压变化较小，不管初始围压（3 MPa）及高围压（20 MPa）下的渗透率均表现出较小变化幅度，主要是因为龙马溪组岩样硬度较大，即使围压增大，原位闭合裂缝壁面凸起也基本不发生破坏。

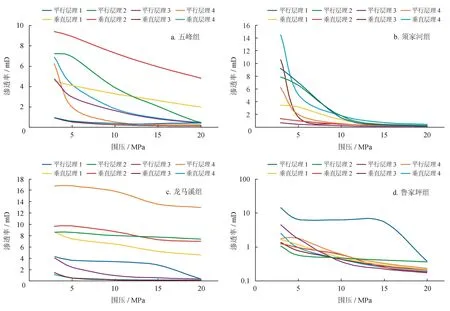
图5 原位闭合型裂缝渗透率测试结果图

2.1.4 鲁家坪组

除平行层理1号岩样外，各组岩心随围压的变化趋势基本一致，在各压力点的差距也不大，最大相差幅度为3.48 mD。对于平行层理1号岩样，主要是因为裂缝面的粗糙度较大，裂缝面上的凸起的结构硬度较大，在较低围压（15 MPa以下），壁面高强度凸起支撑裂缝，高围压（15 MPa以上），壁面高强度凸起破坏，2个裂缝面闭合得更加紧密，渗透率降低。

上述4个页岩层组的岩样，原位闭合型裂缝渗透率与围压的关系，基本符合经典的Walsh理论。

岩样的渗透率与裂缝面分维数关系如图6所示，综合4组岩样结果，岩样的粗糙度越大，岩样的渗透率越大，岩样粗糙度和裂缝渗透率表现出较好的相关性。裂缝的渗透率受表面形貌或粗糙度的控制，根据本文参考文献[8,18]可知平行光滑板之间的流量与缝宽的经典关系式为：

式中Q表示平行光滑板之间的流量，m3/s；h表示平行光滑板之间的距离，m；μ表示流体黏度，mPa·s；p表示压差，Pa；x表示平行光滑板长度，m。

由式（1）可知：缝宽控制裂缝渗透率，原位闭合型裂缝面并不光滑，裂缝表面越粗糙，凸起点越多，缝宽越大，原位闭合裂缝渗透率越高。页岩体积压裂产生了大量壁面比较粗糙的原位闭合裂缝，即使没有支撑剂充填和错位，对于提高储层的产能也同样重要、有效。

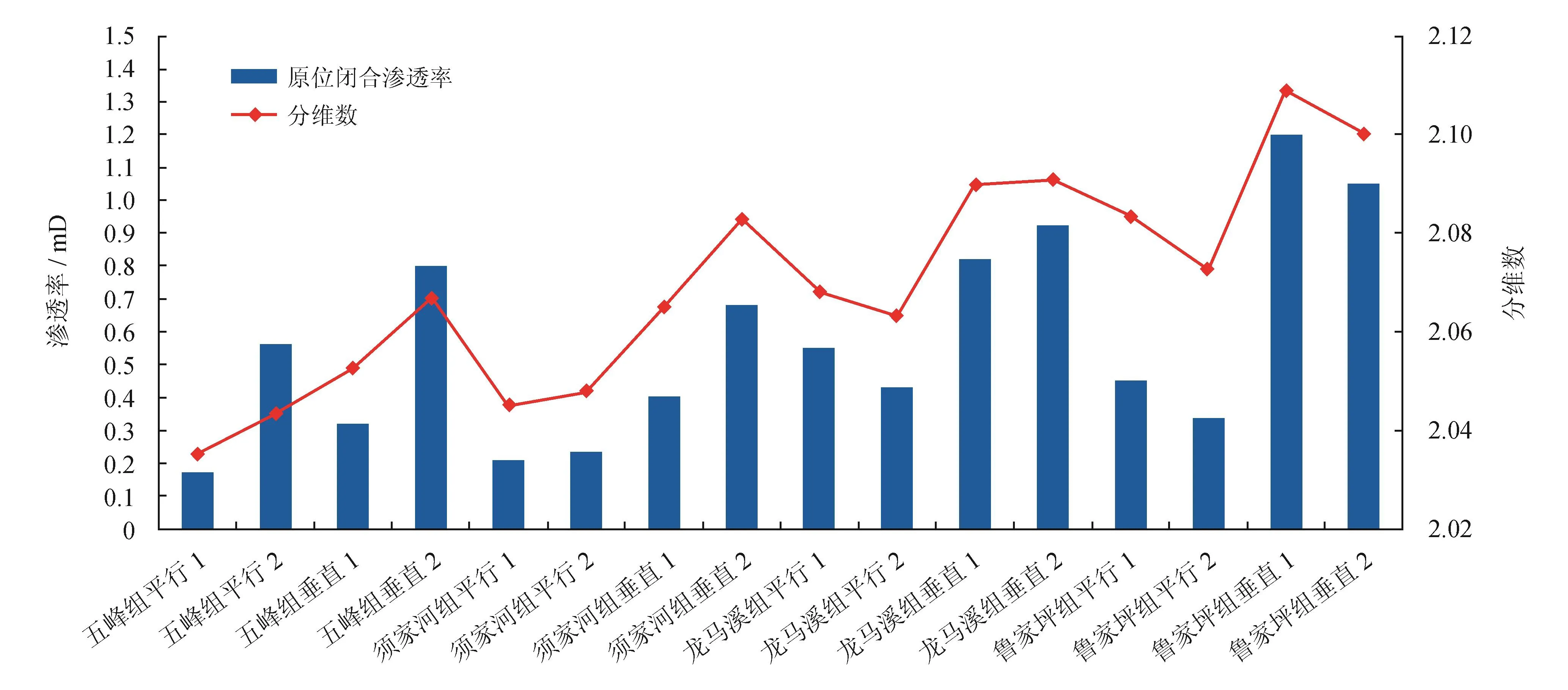
图6 岩样渗透率与分维数关系图

2.2 剪切自支撑型裂缝渗透率

当裂缝的一个面向左或向右发生轻微移动时，缝隙将被错位的凸起点支撑，这种类型的裂缝称为剪切自支撑型裂缝，通过在相反的断面处贴铜箔垫片的方法来产生错位，在3～20 MPa的围压下进行裂缝渗透率测试，实验结果如图7所示。

所测剪切自支撑裂缝渗透率范围为7.53～88.48 mD，较原位闭合渗透率提高1～2个数量级。各层组页岩裂缝渗透率测试结果如下：①五峰组岩样裂缝渗透率明显提高，最大渗透率达到88.48 mD，提高了14.22倍，相对原位闭合型裂缝渗透率结果，8组岩样剪切自支撑裂缝渗透率的差距大幅度减小，每组岩样的渗透率随围压的变化也大幅度减小；②须家河组剪切自支撑裂缝渗透率较原位闭合渗透率在低围压（小于10 MPa）下提高较多，在高围压（大于10 MPa）下提高较少，渗透率随围压的增大而减小得较快；③龙马溪组剪切自支撑裂缝的渗透率，分类比较明显，平行层理的自支撑裂缝渗透率基本不随围压变化，垂直层理的自支撑裂缝渗透率随围压变化较明显；④鲁家坪组剪切自支撑裂缝渗透率整体处于较高的水平，且随围压的增加渗透率变化不大。

剪切自支撑型裂缝渗透率与裂缝面分维数关系如图8所示。图8表明：相同页岩层组岩样，剪切自支撑裂缝渗透率与裂缝面粗糙度表现出正相关关系，但是在不同组之间，高的裂缝表面粗糙度不能完全代表高的渗透率，主要是因为不同组内的岩石矿物组成所表现的粗糙度并不是完全等量，不同矿物组成的岩样的表面凸起等结构的强度不同，其在相同的围压下破碎程度是不同的，因此裂缝的渗透率与岩石的矿物组成及粗糙度均有较大关系。

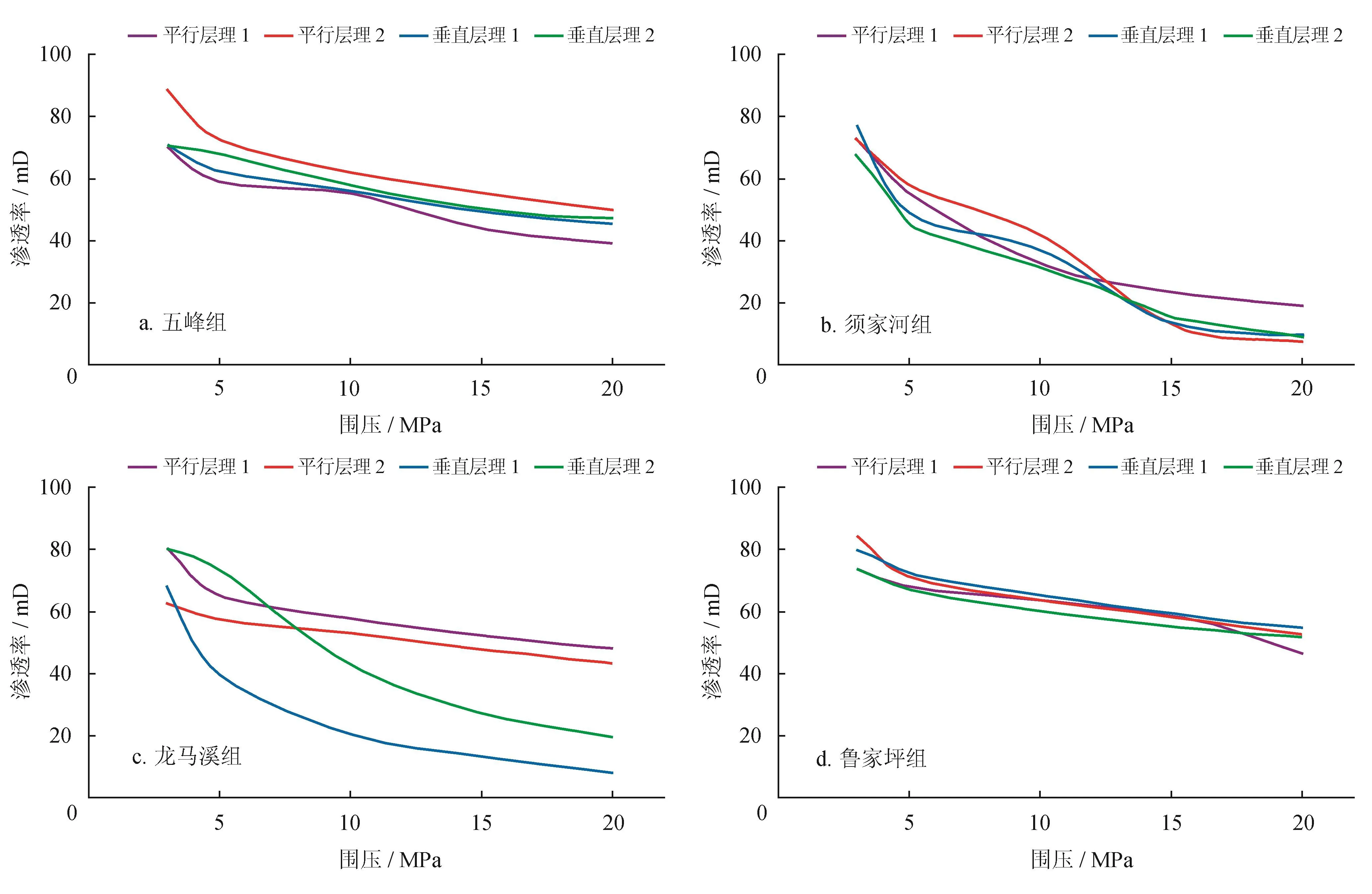
图7 剪切自支撑型裂缝渗透率测试结果图

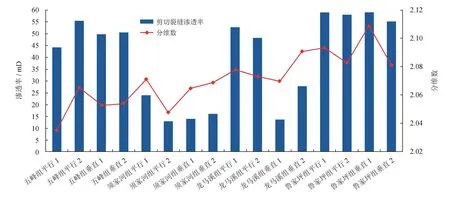
图8 剪切自支撑型裂缝渗透率与分维数关系图

2.3 单层支撑型裂缝渗透率

在剪切自支撑裂缝的基础上，采用40/70目的陶粒，铺砂浓度为0.25 kg/m2进行单层均匀铺置，所测单层支撑型裂缝渗透率值如图9所示。

所测单层支撑型裂缝渗透率的范围为9.98～771.82 mD，较原位闭合型裂缝渗透率提高2～3个数量级，对渗透率的提高效果明显。表现在：①五峰组渗透率提高率幅度最大，五峰组平行层理2号岩样3 MPa下的渗透率达到771.82 mD，较原位闭合渗透率提高2个数量级，组内渗透率差别不大，且随围压变化的趋势相同；②须家河组组内渗透率差别不大，且其随围压变化的趋势呈现一致性；③龙马溪组除平行层理1号岩样外，其余岩样的渗透率随围压变化不大，平行层理和垂直层理之间渗透率差距较大；④鲁家坪组组内渗透率基本一致，随围压变化的趋势也基本一致。

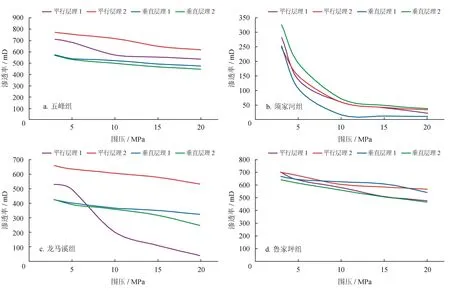
图9 单层铺置支撑剂裂缝渗透率测试图

3 裂缝渗透率变化规律

裂缝渗透率的压力依存性控制着最终的增产表现。笔者利用Walsh理论模型对实验结果进行了分析，该模型用于描述两个粗糙表面间的裂缝渗透率与压力的关系。即

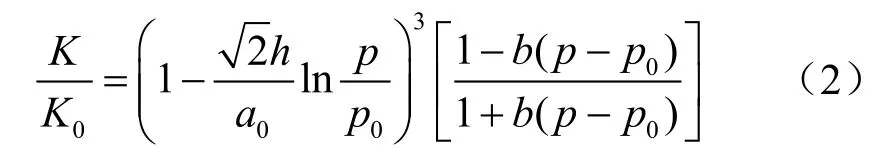
式中K表示瞬时裂缝渗透率，D；K0表示裂缝初始渗透率，D；h表示粗糙高度，m；a0表示初始缝宽，m；p表示瞬时压力，MPa；p0表示初始压力，MPa；b表示接触面积与裂隙面积的比值随压力的变化值，无量纲。

如果b=0，则表明粗糙度几乎不随压力而改变。于是，公式简化为：

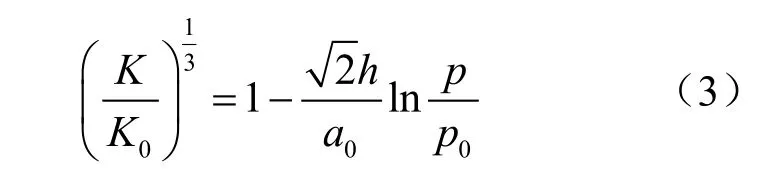
以鲁家坪组岩样渗透率与压力变化关系为例，按照上述方法进行分析，分析结果如图10所示。图10表明：①原位闭合型裂缝。渗透率在3～20 MPa的范围内基本表现呈线性，渗透率与压力的关系符合Walsh理论。②剪切自支撑裂缝。平行层理1号岩样在5～15 MPa范围内表现出线性，主要因为构成裂缝面粗糙高度的凸起的破坏存在阶段性，在小围压下，凸起的部分被破坏，剩余凸起有一定的强度，在5～15 MPa范围内不发生破坏，围压大于15 MPa后凸起被进一步破坏，使裂缝面的粗糙度产生变化，进而导致裂缝的渗透率变化，其余3组岩样在10～20 MPa表现出线性，因为裂缝面的凸起在低于10 MPa的围压下不断被破坏，大于10 MPa后不被破坏。③单层支撑型裂缝。垂直层理1号岩样在5～15 MPa范围表现出线性，低于或高于此范围为非线性，低压下可能反映裂缝的闭合和支撑剂的重新排列等，而高压下可能反映支撑剂的嵌入和部分破碎等，其余3组岩样在10～20 MPa范围表现线性，分析认为，围压大于10 MPa后，裂缝内的支撑剂已稳定不再发生运移等，裂缝面的粗糙度不发生变化，相应的渗透率也基本不发生变化。

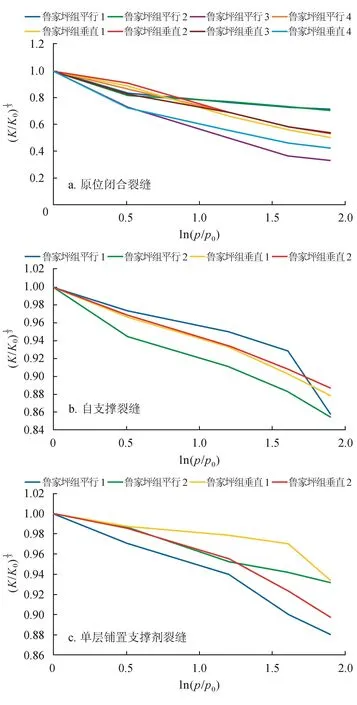
图10 鲁家坪组页岩裂缝渗透率与压力关系图

4 认识与结论

本文针对不同类型页岩压裂裂缝的渗透率进行了测试，测试条件参考威远浅层页岩的埋深、地应力及压后生产压力，得出的实验结果对1 500 m左右的浅层页岩的压裂设计有较好的指导意义。

1）同组页岩垂直层理的裂缝面粗糙度大于平行层理的裂缝面粗糙度，同时裂缝面的粗糙度基本随碳酸盐岩含量的增加而变大。

2）页岩原位闭合裂缝渗透率范围为0.13～16.75 mD；同组页岩原位闭合裂缝渗透率和粗糙度基本呈现正相关关系；不同组之间页岩由于岩石物理力学性质不同，裂缝渗透率随围压增大而减小的幅度不同，组内渗透率的差异也不同；页岩体积压裂产生了大量壁面粗糙的原位闭合裂缝，该类型裂缝即使没有支撑剂充填和错位，对于提高储层的产能也同样重要、有效。

3）页岩自支撑裂缝渗透率范围为7.53～88.48 mD，较原位闭合裂缝渗透率提高了1～2个数量级；同组页岩表面粗糙度大的裂缝，其自支撑裂缝渗透率也较高；不同组内，因岩石矿物组成不同，无此规律。

4）页岩单层铺置支撑剂裂缝渗透率范围为9.98～771.82 mD，较原位闭合渗透率提高2～3个数量级，对渗透率的提高效果非常明显。

5）原位闭合裂缝渗透率与压力的关系符合Walsh理论，而自支撑裂缝渗透率和单层铺置支撑剂渗透率只在一定的压力范围内符合Walsh理论，偏移反映了支撑剂的不稳定排列、嵌入和破碎，自支撑点破碎、颗粒运移等现象，这与渗透率的不断变化相吻合。

[ 1 ] Bowker KA. Barnett shale gas production, Fort Worth Basin: Issues and discussion[J]. AAPG Bulletin, 2007, 91(4): 523-533.

[ 2 ] Gale JFW, Reed RM & Holder J. Natural fractures in the Barnett shale and their importance for hydraulic fracture treatments[J].AAPG Bulletin, 2007, 91(4): 603-622.

[ 3 ] 姜在兴, 张文昭, 梁超, 王永诗, 刘惠民, 陈祥. 页岩油储层基本特征及评价要素[J]. 石油学报, 2014, 35(1): 184-196.Jiang Zaixing, Zhang Wenzhao, Liang Chao, Wang Yongshi, Liu Huimin & Chen Xiang. Characteristics and evaluation elements of shale oil reservoir[J]. Acta Petrolei Sinca, 2014, 35(1): 184-196.

[ 4 ] 刘玉章, 修乃岭, 丁云宏, 王欣, 卢拥军, 窦晶晶, 等. 页岩储层水力裂缝网络多因素耦合分析[J]. 天然气工业, 2015,35(1): 61-66.Liu Yuzhang, Xiu Nailing, Ding Yunhong, Wang Xin, Lu Yongjun, Dou Jingjing, et al. Multi-factor coupling of hydraulic fracture network in a shale gas reservoir[J]. Natural Gas Industry,2015, 35(1): 61-66.

[ 5 ] 尹丛彬, 李彦超, 王素兵, 熊雨然, 何封, 秦俐. 页岩压裂裂缝网络预测方法及其应用[J]. 天然气工业, 2017, 37(4): 60-68.Yin Congbin, Li Yanchao, Wang Subing, Xiong Yuran, He Feng& Qin Li. Methodology of hydraulic fracture network prediction in shale reservoirs and its application[J]. Natural Gas Industry,2017, 37(4): 60-68.

[ 6 ] Martineau DF. History of the Newark East Field and the Barnett shale as a gas reservoir[J]. AAPG Bulletin, 2007, 91(4): 399-403.

[ 7 ] Cipolla CL, Weng Xiaowei, Mack MG, Ganguly U, Gu Hongren,Kresse O, et al. Integrating microseismic mapping and complex fracture modeling to characterize hydraulic fracture complexity[C]//paper 140185-MS presented at the SPE Hydraulic Fracturing Technology Conference, 24-26 January 2011, The Woodlands, Texas, USA. DOI: http://dx.doi.org/10.2118/140185-MS.

[ 8 ] 曾顺鹏, 张国强, 韩家新, 袁彬, 王彦鹏, 冀政. 多裂缝应力阴影效应模型及水平井分段压裂优化设计[J]. 天然气工业,2015, 35(3): 55-59.Zeng Shunpeng, Zhang Guoqiang, Han Jiaxin, Yuan Bin, Wang Yanpeng & Ji Zheng. Model of multi-fracture stress shadow effect and optimization design for staged fracturing of horizontal wells[J]. Natural Gas Industry, 2015, 35(3): 55-59.

[ 9 ] Fredd CN, McConnell SB, Boney CL & England KW. Experimental study of fracture conductivity for water-fracturing and conventional fracturing applications[J]. SPE Journal, 2001, 6(3):288-298.

[10] Kranzz RL, Frankel AD, Engelder T & Scholz CH. The permeability of whole and jointed Barre Granite[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1979, 16(4): 225-234.

[11] Tsang YW & Witherspoon PA. The dependence of fracture mechanical and fluid flow properties on fracture roughness and sample size[J]. Journal of Geophysical Research, 1983, 88(B3):2359-2366.

[12] Gangi AF. Variation of whole and fractured porous rock permeability with conf i ning pressure[J]. International Journal of Rock Mechanics and Mining Science & Geomechanics Abstracts,1978, 15(5): 249-257.

[13] Walsh JB. Effect of pore pressure and conf i ning pressure on fracture permeability[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1981, 18(5):429-435.

[14] 唐颖, 邢云, 李乐忠, 张滨海, 蒋时馨. 页岩储层可压裂性影响因素及评价方法[J]. 地学前缘, 2012, 19(5): 356-363.Tang Ying, Xing Yun, Li Lezhong, Zhang Binhai & Jiang Shixin.Inf l uence factors and evaluation methods of the gas shale fracability[J]. Earth Science Frontiers, 2012, 19(5): 356-363.

[15] Barton N, Bandis S & Bakhtar K. Strength, deformation and conductivity coupling of rock joints[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1985, 22(3): 121-140.

[16] Makurat A, Gutierrez M & Backer L. Fracture fl ow and fracture cross fl ow experiments[J]. Norwegian Petroleum Society Special Publications, 1996, 7: 139-148.

[17] 郭天魁, 张士诚, 刘卫来, 赖文旭. 页岩储层射孔水平井分段压裂的起裂压力[J]. 天然气工业, 2013, 33(12): 87-93.Guo Tiankui, Zhang Shicheng, Liu Weilai & Lai Wenxu. Initiation pressure of multi-stage fracking for perforated horizontal wells of shale gas reservoirs[J]. Natural Gas Industry, 2013,33(12): 87-93.

[18] Penny GS. An evaluation of the effects of environmental conditions and fracturing fluids upon the Long-term conductivity of proppants[C]//paper 16900-MS presented at the SPE Annual Technical Conference and Exhibition, 27-30 September 1987,Dallas, Texas, USA. DOI: http://dx.doi.org/10.2118/16900-MS.

[19] Brown SR. Fluid fl ow through rock joints: the effect of surface roughness[J]. Journal of Geophysical Research, 1987, 92(B2):1337-1348.

[20] Zhou HW & Xie H. Direct estimation of the fractal dimensions of a fracture surface of rock[J]. Surface Review and Letters, 2003,10(5): 751-762.

[21] 张亚衡, 周宏伟, 谢和平. 粗糙表面分形维数估算的改进立方体覆盖法[J]. 岩石力学与工程学报, 2005, 24(17): 3192-3196.Zhang Yaheng, Zhou Hongwei & Xie Heping. Improved cubic covering method for fractal dimensions of a fracture surface of rock[J]. Chinese Journal of Rock Mechanics and Engineering,2005, 24(17): 3192-3196.

[22] Guo Tianku, Zhang Shicheng, Gao Jun, Zhang Jingchen & Yu Haiqing. Experimental study of fracture permeability for Stimulated Reservoir Volume (SRV) in shale formation[J]. Transport in Porous Media, 2013, 98(3): 525-542.