人口结构变动对时间偏好的影响分析

欧明青，倪宣明，韦 江

(1.清华大学经济管理学院，北京 100084；2.北京大学软件与微电子学院，北京 100871)

1 引言

如果一个国家或地区60周岁及以上老年人口占人口总数的10%，或者65岁及以上老年人口占人口总数的7%，该国家或地区就被认为进入了老龄化社会。根据当前我国统计局对老年人口的统计，2001年我国65岁及以上老年人口占总人口的比例为7.1%，表明我国已正式进入老龄化社会。而且这个老年人口比例还在逐年上升，依据《2016年社会服务发展统计公报》，我国60周岁及以上老年人口占总人口比例为16.7%，65周岁及以上老年人口占总人口比例已达10.8%，并预期未来老龄化程度会进一步加深。因此人口老龄化已成为影响我国经济发展的重要因素之一。

老年人占比的变化即人口结构的变动形成了当前的人口老龄化问题。而我国老年人口基数大，增长速度较快，老年人的养老支出逐年上升，使得经济的总储蓄率下降，资本积累速度下降，投资也下降，从而导致经济增长速度下滑。近年来我国GDP整体增速变缓，人口老龄化程度不断加深显然是重要因素之一。这种人口结构的老龄化变动使得劳动生产力的供给整体下滑，劳动人口占总人口的比重越来越低，并具有持续下降趋势，也会使得政府的政策与人们的观念均发生变化，因此人口结构的变化会影响人们对未来的看法，即人口结构的变化会影响时间偏好，即影响效用贴现因子。因此本文从人口结构和时间偏好的角度来建立老龄化的经济增长模型。

对经济增长理论的分析始于Harrod[1]，基于“资本产出比不变”这一关键假设，将经济增长率分为实际增长率、均衡增长率与自然增长率，这三个增长率均由外生参数决定，很难同时相等，因此，增长路径呈现“刀锋式”形态，难以稳定。Solow[2]用新古典生产函数代替了Harrod[1]的生产函数假设，构建了新古典增长理论，即经济系统全局稳定，在该平衡增长路径上，人均产出唯一取决于技术进步率，从而改变了Harrod[1]的悲观结论。随后，Cass[3]和Koopman[4]在Ramsey[5]研究的基础上，将Solow模型中外生的储蓄率内生化，引进代表性家庭假设，并在Samuelson[6]效用可加、时间可分、偏好一致及效用贴现因子不变的假设下，将Solow模型的一维微分系统拓展为二维微分系统，得出鞍型(Saddle)的平衡增长路径，这种鞍型路径正反映了代表性家庭的理性。Ramsey模型还可以对家庭的效用函数及企业的生产函数进行拓展，如Sidrauski[7]基于Tobin[8]模型将货币引入效用函数，Kurz[9]将财富引入效用函数，Arrow和Kurz[10]和Barro[11]将政府公共支出引入效用函数和生产函数，Cole等[12]将社会地位引入效用函数，Turnovsky[13]将劳动引入效用函数等。

但利用Ramsey模型求解家庭效用最大化问题时，若不考虑人口增长、技术进步等因素，给定资本回报率为常数，那么微分系统中资本回报率与效用贴现因子这两个外生参数如果不相等，将会产生动态无效，但相等又将出现无动态。因此，需要对Samuelson[6]的效用贴现因子假设进行拓展，主要有内生和外生两个方向。效用贴现因子反映家庭对未来的看法，内生化方向上将效用贴现因子表示为系统内生变量的函数，效用贴现因子随着内生变量的变化加以调整。Uzawa[14]指出，效用贴现因子受家庭效用的影响，而效用受消费影响。Obstfeld[15]将Uzawa[14]的研究方法直接推广到开放经济系统。Becker和Barro[16]指出幸福程度影响贴现因子。Becker和Mulligan[17]指出健康、不确定性、死亡率等都会影响效用贴现因子，家庭可以通过投资来改变对未来的看法。Gootzeit等[18]指出储蓄水平影响家庭对未来的耐心程度，并认为这是Marshall的观点，因此将这种贴现因子称为Marshall贴现因子。Kam[19]指出财富会影响贴现因子。但是，内生化方向在技术上难以处理，对效用贴现因子函数的假设也更为严格，不如外生化方向便利。Laibson[20]提出了双曲线贴现因子(Hyperbolic discounting)，认为家庭在今天和明天之间耐心程度较低，更为看重今天，但明天和将来之间耐心程度较高，甚至未来无差异。Barro[21]在Laibson[20]基础上研究承诺能力(Commitment)。Takashi[22]提出非线性贴现因子(Nonlinear discounting)。Krusell和Smith[23]提出拟几何级数贴现因子(Quasi-geometric discounting)。

Ramsey模型将经济增长归结为外生的技术进步率，内生增长率理论则将技术进步率内生化，探究经济增长的微观机制，将技术进步主要归结为人口的增长。Arrow[24]提出了干中学(Learning by doing)模型，指出技术可以在生产产品的过程中附带产生，这就改变了新古典生产函数的基本假设，如使用AK型生产函数。Uzawa[25]建立了产品生产和人力资本生产的两部门经济模型，人力资本的生产过程与物质产品的生产过程类似。这两个基本模型均指出，技术进步唯一取决于人口增长。显然，若发明技术的成本独立于使用技术的人数，随着人口规模的增加，技术发明的潜在人数将会增加，技术的总量将会上升。随后，Romer[26-27]和Lucas[28-29]分别对这两个基本模型加以拓展，前者指出除人口增长外，政府对研发的投入、制度建设及经济一体化等因素也会促进技术进步，后者指出人力资本存在溢出效应，分别形成了Arrow-Romer模型与Uzawa-Lucas模型。Aghion和Howitt[30]也给出类似的观点。人口增长促进技术进步的同时，技术进步也会影响人口增长，Kremer[31]研究指出，在几乎全部的人类历史中，技术进步主要用于人口增加而非人均收入增加。

Ramsey模型假定了代表性消费者的同质性，并认为消费者永续存在(Infinite horizon)，要想在经济系统中分析老年人，需要对这种假设加以改变。Ramsey模型中与人口相关的基本假设，有代表性家庭假设与总人口增长率与劳动人口增长率相等假设。Samuelson[32]和Diamond[33]改变代表性消费者永续存在假设，直接引入老年人，指出代表性消费者只存在两期，分别表示为年轻人和老年人，年轻时进行储蓄以便老年时消费，在两类人口结构平稳的前提下建立OLG模型进行分析。这是当前国内外研究老龄经济的主流范式，例如在OLG模型基础上，Futagami和Nakajima[34]结合生命周期假说分析老龄化问题，刘穷志和何奇[35]、Nishiyama[36]研究老龄化与财政政策的关系，胡翠和许召元[37]研究老龄化与储蓄率之间的关系，Mao Rui和Xu Jianwei[38]研究老龄化与消费率之间的关系，Fougere等[39]、Choi和Shin[40]直接进行实证分析。此外，Blanchard[41]在Yarri[42]的基础上，在经济模型中引入死亡率假设，这改变了代表性家庭永续存在这一假设，以间接的方式变相引入了老年人。另一种间接方式由武康平等[43-44]给出，通过放宽Ramsey模型中“总人口增长率与劳动人口增长率相等”这一假设，引入人口结构变动，指出人口老龄化的形成总与人口某一阶段快速增长相关，并将总人口增长率与劳动人口增长率之差定义为老龄化率，在此基础上分析老龄经济，此时将经济系统中未被劳动吸收的新增加的人口视为老年人，而且人口结构持续变动，这样不必引入年龄结构参数。本文正是在这一假设基础之上研究人口结构变化对效用贴现因子及经济增长与社会福利的影响，并从以下方面区别于既有文献的研究工作。

第一，我们从人口结构的持续变动出发，在经济学上而非统计学意义上定义老龄化率，并在此基础上定义人口结构变动参数。第二，人口结构变动会影响人们对未来的看法，即影响效用贴现因子，我们引入人口结构的变动对既有的增长理论模型进行了拓展。因为增长理论一般都假设一个代表性家庭和一个代表性企业，即经济系统中的家庭或企业是同质的。但由于代表性家庭又被假定永续存在，那么人口结构变动对代表性的家庭或者个体没有意义，因此在这种假定下人口增长率的变化、人口结构的变动等都无法影响效用贴现因子，而这与现实的经济运行不符合。我们引入人口结构变动后，可以刻画人口结构对效用贴现因子的影响，从而拓展现有的增长理论模型使之更符合实际情况。第三，根据我们的模型可以直观的从理论上探讨人口结构变动对社会福利及经济增长的影响。更进一步的证明如果用代表性家庭的终身效用来度量社会福利，由于人口结构也影响效用贴现因子，社会福利最大化与经济增长速度最大化将会呈现不一致。第四，从社会福利最大化和经济增长速度最大化两个角度出发，我们给出了对人口政策及老龄化问题相应的政策建议，并在一定的假设下，给出了最优的人口结构参数。

本文的内容安排如下：给出理论分析所需要的基本假设，包括老龄化率、人口结构变动、效用贴现因子等；建立分散经济框架下的理论模型，探讨人口结构变动对经济增长及社会福利的影响，并给出相应的数值模拟。另一方面，理论分析和数值模拟的结果也可以为政府制定相应的政策提供依据。

2 模型假设

通过放宽Ramsey模型中“总人口增长率与劳动人口增长率相等”这一假设，引入人口结构变动，将总人口增长率与劳动人口增长率之差定义为老龄化率，将经济系统中未被劳动吸收的新增加的人口视为老年人，而且人口结构持续变动，这样不必引入年龄结构参数，在此基础之上研究人口结构变化对效用贴现因子及经济增长与社会福利的影响。

2.1 老龄化率

假设劳动人口是总人口的一定比例，即L(t)=φ(t)P(t)，L(t)与P(t)表示t时刻的劳动人口与总人口。比例φ(t)并非常数，总人口增长率与劳动人口增长率不相等，将经济系统中持续增加的非劳动人口定义为老年人，则老龄化率θ的定义如下：

(1)

2.2 人口结构参数

因为我国已经进入老龄化社会，也即θ>0，但是经济系统中老年人口总量以增速θ持续上升，也意味着我国的人口结构也在持续发生变动，这种结构变化可以用老年人口与劳动人口的增速之比来度量。又因为二者增速之间满足关系式θ+l=n，因此我们将人口结构参数λ定义为老年人口与总人口的增长速度之比：

(2)

2.3 技术

内生增长理论将技术进步主要归结为人口的增长。Arrow-Romer的干中学模型表明知识可以在生产物质产品过程中伴随产生，而Uzawa-Lucas的两部门经济模型表明技术的生产过程与物质产品的生产过程类似，两部门之间的资源配置对经济系统有影响。由于知识普遍具有非竞争性和非排他性的公共品属性，既有的知识存量也会对技术进步产生影响。

如果忽略财富、研发投入、基础教育投入、制度等因素对技术进步的影响，仅考虑人口因素，则技术进步率可以表示为：

(3)

其中，A表示技术或知识，初始的技术存量为A0。n-θ是劳动人口的增长速度，可以视为干中学效应。老年人往往拥有较高的人力资本，尤其体现在智慧上，如大学教授、中医等，因此θ某种程度上也可视为两部门模型中生产技术的资源投入。这里，技术进步率使用人口结构参数来度量，因此(3)式可改为：

(4)

参数θ与n已外生给定，则g(λ)>0也为外生给定。

2.4 效用贴现因子

时间偏好，即效用贴现因子，反映代表性家庭对未来的看法。假设效用贴现因子ρ受人口结构的影响，即：

ρ=ρ(λ)

(5)

假设ρ(λ)在[0,1]上可导，并在(0,1)上该导数连续。假设人口增长率小幅上升，形成的额外的老龄化率的上升超过人口增长率，当λ小幅上升，人们预期额外增加的人口所形成的技术进步成果更高，会对未来极为有耐心，更看重未来，此时ρ′(λ)<0；但是如果经济系统中老龄化率占人口增长率的比例过高，人们预期未来的技术进步率不足以支撑老年人口，从而会担心未来，此时更看重当前，即ρ′(λ)>0。假设这种不安会随着老龄化率占比上升而加深，因此不妨假设ρ″(λ)>0。例如，放开二胎政策，一对夫妇可生两胎时，相比较一胎而言，对未来的担心程度会降低，比如至少“失独”家庭的可能性会降低。但若夫妇生五六胎甚至更多时，如类似建国后初期人口的快速增长，则会使社会形成对未来养老问题的担忧，甚至会担心进入马尔萨斯陷阱，从而更会看重当前。

当人口结构参数λ给出时，ρ(λ)也为外生常数。

2.5 其它相关假设

假设代表性消费者具有CRRA型效用函数为u(C)=C1-δ/(1-δ)，δ∈(0,1)为常数表示不变的相对风险规避倾向。经济系统中代表性家庭永续存在且家庭数量Z不发生变化，人口在家庭内增长，则代表性家庭的终身效用可以表示为：

(6)

家庭的收入来源包括劳动(L)收入与资产(B)收入，有效劳动(AL)的工资率w，资产的收益率为常数r，初始资产为B0。

假设代表性企业的生产函数Y=F(K,AL)满足新古典函数假设，即生产函数对资本和劳动一次齐次、K与L的边际生产率为正并递减、Inada条件等。

经济系统不考虑政府、折旧等因素。

3 理论模型与福利分析

3.1 理论模型

首先定义有效劳动人均下的集约形式：k=K/(AL)，c=PC/(AL)，b=B/(AL)，f(k)=Y/(AL)=F(k,1)，在代表性家庭与代表性企业优化行为的基础上，分析平衡增长路径。

代表性家庭考虑终身效用最大化，优化问题如下：

(7)

其中，D=(A0φ0)1-δP0/Z，β=ρ(λ)-n-(1-δ)(g(λ)-θ)为有效劳动人均化后的效用贴现因子，假设β>0，用以保证广义积分收敛，b0=φ(c0)表示代表性家庭收支平衡下，初始有效劳动资产与初始有效劳动人均消费所满足的函数关系。

定义Hamilton函数为H=Dc1-δe-βt/(1-δ)+μ(rb+w-c-(n+g(λ)-θ)b)，其中μ为Hamilton乘子，表示有效劳动人均资产b的边际值。

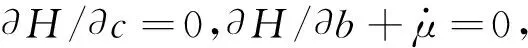
(8)

这里未给出生产函数的具体形式，微分系统难以求出显式解，仅考虑稳态点及平衡增长路径，并忽略对横截性条件的讨论。

代表性企业追求利润最大化，优化问题如下：

(9)

一阶必要条件在集约化下的形式为：

r=f′(k)，w=f(k)-kf′(k)

(10)

市场出清要求企业资本需求与家庭资产供给相等，即：

b=k

(11)

结合式(8)与式(10)，经济系统由下述微分方程组决定：

(12)

3.2 平衡增长路径

(13)

由生产函数的单调性假设f′(k)>0，均衡点的存在需要满足以下前提条件：

ρ(λ)+δ(g(λ)-θ)>0

(14)

基于式(14)，均衡点满足存在性和唯一性，进一步分析考虑经济系统的稳定性。将式(12)中的微分方程组在均衡点(k*,c*)附近一阶泰勒展开，对应系数矩阵的特征方程为：

η2-βη+c*f″(k*)/σ=0

(15)

其中，η表示系数矩阵的特征根，由η1η2=c*f″(k*)/σ<0和η1+η2=β>0，可知特征根一正一负，表明经济系统在均衡点附近鞍点稳定，与标准的Ramsey模型类似，且这种鞍型路径正反映了代表性家庭的理性选择行为。不妨假设η1<0，则-η1可以表示经济系统从初始状态到均衡点的近似收敛速度。

(16)

此时，总产出与总资本均以n+g(λ)-θ的速度增长，但劳动人均产出的增长率与人均产出的增长率并不相同。劳动人均产出的增长率为：

(17)

而人均产出(yP)的增长率为：

(18)

即人均产出增长率取决于技术进步率和老龄化率之差，显然，人均产出持续上升，前提条件必须满足：

g(λ)>θ

(19)

技术增长率必须超过老龄化率。一旦g(λ)=θ，人均产出陷入停滞，技术进步带来的成果由老龄化率完全吸收，而若g(λ)<θ，人均产出将持续下降，最终将会陷入马尔萨斯陷阱。

平衡增长路径的基本分析由定理1总结：

定理1：给定ρ(λ)+δ(g(λ)-θ)>0，总产出和总资本以n+g(λ)-θ的速度增长，若g(λ)>θ，人均产出以g(λ)-θ的速度增长，取决于技术进步率与老龄化率之差；若g(λ)=θ，技术进步带来的成果完全由老龄化率吸收；若g(λ)<θ，经济会陷入马尔萨斯陷阱。

3.3 社会福利与经济增长

基于代表性家庭存在，社会福利可以由家庭的终身效用表示，在平衡增长路径上，社会福利表示为：

U*=Du(c*)/β

(20)

由式(18)，经济增长速度可由人均收入(产出)的增长速度表示：

γ=g(λ)-θ

(21)

经典的Ramsey模型中一般假设β为常数，社会福利仅取决于效用，基于效用函数的单调性，效用u(c*)最大化意味着c*的最大化，而后者与y*的最大化一致，此时社会福利最大化与经济增长速度一致。当效用函数或生产函数发生变化时，如Sidrauski或Barro，二者会呈现不一致。但在本模型中，由于人口结构影响了效用贴现因子ρ进而影响β，此时，福利最大化与增长速度最大化将会呈现不一致。

依式(2)中人口结构参数的定义，人口结构受总人口增长率及老龄化率的影响。依式(1)老龄化率的定义，总人口增长率分解为老龄化率与劳动人口增长率，因此，可以假设θ与l均为n的函数，分别表示为θ(n)与l(n)，进而人口结构参数λ也为总人口增长率n的函数。假设λ(n)、θ(n)和l(n)在[0,∞)上可导，并在(0,∞)上导数连续，θ′(n)∈[0,1]。当θ′(n)=0时，表明总人口增长率上升全部为劳动人口增长率所吸收；当θ′(n)=1时，表明总人口增长率上升全部为老龄化率所吸收；当θ′(n)∈(0,1)时，总人口增长率上升使得老龄化率与劳动人口增长率同时上升。下面考虑人口增长率变化对经济系统的影响。

定理2：若(ρ′(λ)+δg′(λ))λ′(n)-δθ′(n)>0，则劳动人均资本随总人口增长率上升而下降，∂k*/∂n<0；若(ρ′(λ)+δg′(λ))λ′(n)-δθ′(n)<0，则∂k*/∂n>0。若β∂k*/∂n-k*(1+g′(λ)λ′(n)-θ′(n))<0，则劳动人均消费随总人口增长率上升而下降，∂c*/∂n<0；若β∂k*/∂n-k*(1+g′(λ)λ′(n)-θ′(n))>0，则∂c*/∂n>0。其中，∂k*/∂n=(ρ′(λ)+δg′(λ))λ′(n)/f″(k*)-δθ′(n)/f″(k*)。

证明：式(13)两边同时对n求导，可得：

(22)

整理可得定理2。证毕。

下面考虑社会福利最大化。式(20)对总人口增长率求导可得：

(23)

其中，εnc、εcu与εnβ分别表示总人口增长率n对有效劳动人均消费c、有效劳动人均消费c对代表性消费者效用u和总人口增长率n对调整后效用贴现因子β的弹性。式(23)表明，人口增长率对社会福利的影响，取决于其对效用和对效用贴现因子的影响之差。在代表性家庭假设中使用了CRRA型效用函数，易得：

εcu=1-δ

(24)

定理3：若(1-δ)εnc>εnβ，则社会福利随人口增长率上升而上升，∂U*/∂n>0；若(1-δ)εnc<εnβ，∂U*/∂n<0；社会福利最大化的必要条件为：(1-δ)εnc=εnβ。

其中：

(25)

基于定理2及β的定义，对n求偏导并整理，即可完成定理3的证明。

从式(25)可以看出，n对调整后的效用贴现因子β的影响分为三部分：首先是对效用贴现因子ρ(λ)的影响；其次是人口增长的直接影响，因为人口在代表性家庭中增长；最后是对技术进步率的影响，因为分析中使用了劳动人均的集约形式。

由于ρ(λ)的存在，社会福利最大化与经济增长最大化呈现不一致。人口增长率对经济增长的影响由定理4给出：

定理4：若g′(λ)λ′(n)>θ′(n)，人均收入增速随人口增长率上升而上升，∂γ/∂n>0；若g′(λ)λ′(n)<θ′(n)，则∂γ/∂n<0；人均收入增速最大化必要条件为g′(λ)λ′(n)=θ′(n)。

式(21)中对n求导并整理，即可完成定理4的证明。

定理3与定理4比较易得，社会福利最大化和人均产出增速最大化所要求的总人口增长率很难一致，不一致的条件由定理5给出。

定理5(不一致定理)：总人口增长率不能同时满足社会福利最大化和人均收入增长速度最大化的充分条件为：(1-δ)(βρ′(λ)λ′(n)/f″(k*)-k*)/c*-(ρ′(λ)λ′(n)-1)/β≠0。

定理5的证明中，将人均收入增速最大化必要条件代入社会福利最大化的必要条件，即可证得。

3.4 最优人口结构

前面分析中，人口结构λ取决于人口增长率n，社会福利或人均收入增速最大化决定了最优的人口增长率n，进而也决定了最优的人口结构λ。

这里考虑一种特殊情形以分析人口结构的影响：人口增长率的变动不影响人口结构，λ′(n)=0，即εnθ=1，这表明老龄化率始终为人口增长率的不变比例λ∈(0,1)，θ=λn。

此时，考虑人口结构变动，定理2相应调整为：

定理2’：若ρ′(λ)+δ(g′(λ)-n)>0，则∂k*/∂λ=(ρ′(λ)+δ(g′(λ)-n))/f″(k*)<0；若ρ′(λ)+δ(g′(λ)-n)>0，则∂k*/∂λ<0。若β∂k*/∂λ-k*(g′(λ)-n)<0，则∂c*/∂λ<0；若β∂k*/∂λ-k*(g′(λ)-n)>0，则∂c*/∂λ>0。

人口结构对社会福利的影响相应调整为：

定理3’：若(1-δ)ελc>ελβ，则社会福利随人口结构参数上升而上升，∂U*/∂λ>0；若(1-δ)ελc<ελβ，∂U*/∂λ<0；社会福利最大化的必要条件为：(1-δ)ελc=ελβ。

其中：

(26)

人口结构对经济增长的影响相应调整为：

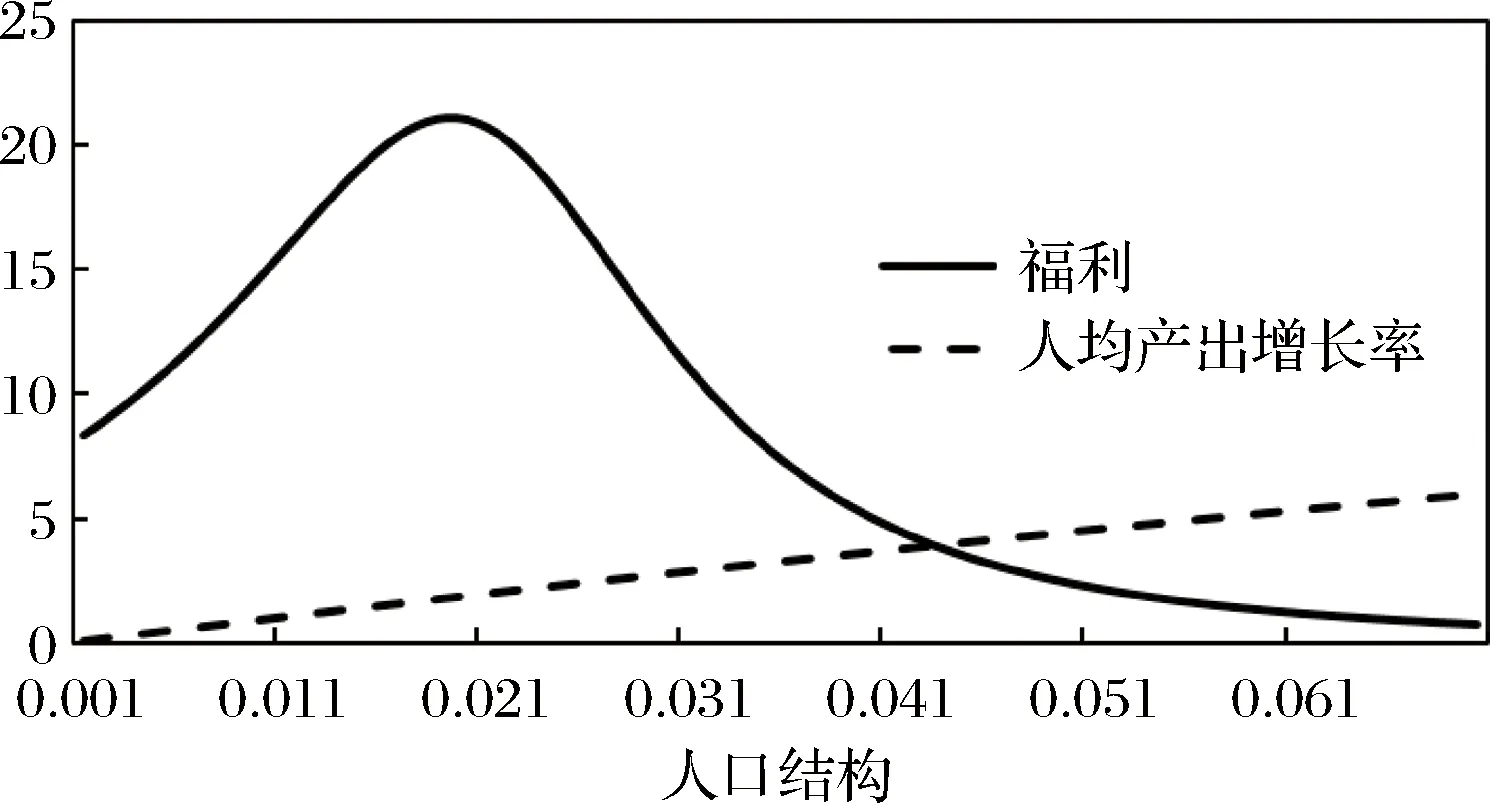
定理4’：若g′(λ)>n，人均收入增速随人口结构参数上升而上升，∂γ/∂n>0；若g′(λ)

为给出人均收入增速最大化下的最优人口结构参数显式解，不妨假设最优技术进步率的函数为：

g(λ)=(1-dλ)λ，d>0

(27)

易得人均收入增速最大化下的最优人口结构参数为：

(28)

式(28)要求n<1，实际经济中，这一条件很容易满足。

为简化分析社会福利，将式(27)给出的技术进步率函数调整为：

g(λ)=λn=θ

(29)

式(29)表明，技术进步率是总人口增长率的固定比例，但低于人口增长率，而且此时技术进步带来的成果完全为老龄化率所吸收，人均产出维持不变。

定理6：若g(λ)=λn，则社会福利最大化的充分条件为：ρ′(λ)=0。

证明：给定g(λ)=λn，依据式(20)及定理3’，整理可得：

(30)

由f″(k*)<0、1-δ>0及效用贴现因子ρ(λ)的相关假设可知，ρ′(λ)=0为社会福利最大化的充分条件。证毕。

这里给出一个简单的函数模拟，假设效用贴现因子的函数为：

ρ(λ)=ρ0+λ(qλ-p)

(31)

其中，ρ0>0，0

当λ

0，最优的人口结构参数为λ=p/2q。

3.5 参数模拟

为了更直观地观察人口增长率对社会福利和经济增长速度的影响，我们采用数值计算来说明。选取参数ρ0=0.02，δ=0.75，λ=0.3，d=2，p=1，q=4，则g(λ)=(1-2λ)λ，ρ(λ)=0.02+λ(4λ-1)。如图1所示，社会福利最大化和经济增长速度最大化所要求的人口增长率是不同的。在选取的参数下，人口结构参数超过p/2q，代表性消费者对未来较为悲观，转而越来越看重当前。

图1 人口增长率对社会福利和人均产出增长率的影响

类似的，用数值模拟的方法观察人口结构对社会福利和人均产出增长率的影响，选取参数ρ0=0.02，δ=0.75，n=0.002，d=2，p=1，q=30，则g(λ)=(1-2λ)λ，ρ(λ)=0.02+λ(30λ-1)。如图2所示，社会福利最大化和经济增长速度最大化所要求的人口结构是不同的。

图2 人口结构对社会福利和人均产出增长率的影响

4 结语

本文根据老龄化这一实际社会现象，从人口结构持续变动出发，放宽“总人口增长率与劳动人口增长率相等”这一基本假设，从经济学角度定义老龄化率，并将人口结构参数定义为老龄化率与人口增长率的比例。人口结构变动不仅影响人们对未来的看法，即效用贴现因子，还影响技术进步率。在一定假设下，我们将人口结构参数引进Ramsey模型，得出鞍型的平衡增长路径。并发现在该路径上，人均产出增长率取决于技术进步率与老龄化率之差。在既定的人口结构下，技术进步除用于提高收入水平外，还用于赡养经济中的老年人口。由于人口结构参数受总人口增长率影响，又影响效用贴现因子，因此经济增长速度最大化与福利最大化所要求的总人口增长率不一致，本文也给出了相应的边界条件。

为分析人口结构参数对经济系统的影响，本文随后考虑一种特殊情形，老龄化率是总人口增长率的固定比例，此时总人口增长率不影响人口结构参数。在给出经济增长速度最大化和社会福利最大化所需人口结构参数的一阶条件基础上，本文进行了相应的函数模拟。经济增长速度最大化要求人口结构参数对技术进步率的边际影响等于总人口增长率。为简化为社会福利的分析，本文给出技术进步率与老龄化率相等的假设，得出对应社会福利最大化的最优人口结构参数的一阶条件，此时人口结构参数对效用贴现因子的边际影响应该等于零。

[1] Harrod R F. An essay in dynamic theory[J]. The Economic Journal, 1939, 49(193):14-33.

[2] Solow R. A contribution to the theory of economic growth[J]. Quarterly Journal of Economics, 1956, 70(1):65-94.

[3] Cass D. Optimum growth in an aggregative model of capital accumulation[J]. Review of Economic Studies, 1965, 32(3):233-240.

[4] Koopmans T C. On the concept of optimal economic growth[M]//Koopmans T C. The Econometric Approach to Development Planning， Amsterdam: North Holland Press, 1965.

[5] Ramsey F P. A mathematical theory of saving[J]. The Economic Journal, 1928, 38(152):543-559.

[6] Samuelson P A. A note on measurement of utility[J]. Review of Economic Studies, 1937, 4(2):155-161.

[7] Sidrauski M. Rational choice and patterns of growth in a monetary economy[J]. American Economic Review, 1967, 57(2):534-544.

[8] Tobin J. Money and economic growth[J]. Econometrica, 1965, 33(4):671-684.

[9] Kurz M. Optimaleconomic growth and wealth effects[J]. International Economic Review, 1968, 9(3):348-357.

[10] Arrow K J, Kurz M. Optimal growth with irreversible investment in a Ramsey model[J]. Econometrica, 1970, 38(2):331-344.

[11] Barro R J. Government spending in a simple model of endogenous growth[J]. Journal of Political Economy, 1990, 98(5):103-125.

[12] Cole H L, Mailath G J, Postlewaite A. Social norms, savings behavior, and growth[J]. Journal of Political Economy, 1992, 100(6):1092-1125.

[13] Turnovsky S. The impact of terms of trade shocks on a small open economy: A stochastic analysis[J]. Journal of International Money and Finance, 1993, 12(3):278-297.

[14] Uzawa H.Time preference, the consumption function and optimum asset holdings[M]//Wolfe J N. Value, capital and growth: Papers in honor of Sir John Hicks, Chicago: Aldine Press, 1968.

[15] Obstfeld M. Macroeconomic policy, exchange-rate dynamics, and optimal asset accumulation[J]. Journal of Political Economy, 1981, 89(6):1142-1161.

[16] Becker G S, Barro R J. A reformulation of the economic theory of fertility[J]. Quarterly Journal of Economics, 1988, 103(1):1-25.

[17] Becker G S, Mulligan C B. The endogenous determination of time preference[J]. Quarterly Journal of Economics, 1997, 112:729-758.

[18] Gootzeit M, Schneider J, Smith W. Marshallian recursive preferences and growth[J]. Journal of Economic Behavior and Organization, 2002, 49(3):381-404.

[19] Kam E. A note on time preference and the Tobin effect[J]. Economics Letters, 2005, 89(1):127-132.

[20] Laibson D. Golden eggs and hyperbolic discounting[J]. Quarterly Journal of Economics, 1997, 112(2):443-477.

[21] Barro R J. Ramsey meets Laibson in the neoclassical growth model[J]. Quarterly Journal of Economics, 1999, 114(4):1125-1152.

[22] Takashi K. Externalities and nonlinear discounting: Indeterminacy[J]. Journal of Economic Dynamics and Control, 2002, 26(1):141-169.

[23] Krusell P, Smith A. Consumption-savings decisions with quasi-geometric Discounting[J]. Econometrica, 2003, 71(1):365-375.

[24] Arrow K J. The economic implication of learning by doing[J]. Review of Economic Studies, 1962, 29:155-173.

[25] Uzawa H. Optimal technical change in an aggregative model of economic growth[J]. International Economic Review, 1965, 6(1):18-31.

[26] Romer P. Increasing return and long-run growth[J]. Journal of Political Economy, 1986, 94(10):1002-1037.

[27] Romer P. Endogenous technological change[J]. Journal of Political Economy, 1990, 98(5):71-102.

[28] Lucas R. On the mechanics of economic development[J]. Journal of Monetary Economics, 1988, 22(1):3-42.

[29] Lucas R. Making a miracle[J]. Econometrica, 1993, 61(2):251-272.

[30] Aghion P, Howitt P. A model of growth through creative destruction[J]. Econometrica, 1992, 60(2):323-391.

[31] Kremer M. Population growth and technological change: One million BC to 1990[J]. Quarterly Journal of Economics, 1993, 108(3):681-716.

[32] Samuelson P A. An exact consumption-loan model of interest with or without the social contrivance of money[J]. Journal of Political Economy, 1958, 66(6):467-482.

[33] Diamond P. National debt in a neoclassical growth model[J]. American Economic Review, 1965, 55(5):1126-1150.

[34] Futagami K, Nakajima T. Population aging and economic growth[J]. Journal of Macroeconomics, 2001, 23(1), 31-44.

[35] 刘穷志, 何奇. 人口老龄化, 经济增长与财政政策[J]. 经济学(季刊), 2013, 12(1):119-134.

[36] Nishiyama S. Fiscal policy effects in a heterogeneous-agent OLG economy with an aging population[J]. Journal of Economic Dynamics and Control, 2015, 61:114-132.

[37] 胡翠, 许召元. 人口老龄化对储蓄率影响的实证研究——来自中国家庭的数据[J]. 经济学(季刊), 2014, 13(4):1245-1364.

[38] Mao Rui, Xu Jianwei. Population aging, consumption budget allocation and sectoral growth[J]. China Economic Review, 2014, 30:44-65.

[39] Fougere M, Harvey S, Mercenier J, et al. Population ageing, time allocation and human capital: A general equilibrium analysis for Canada[J]. Economic Modelling, 2008, 26(1):30-39.

[40] Choi K H, Shin S. Population aging, economic growth, and the social transmission of human capital: An analysis with an overlapping generations model[J]. Economic Modelling, 2015, 50(2):138-147.

[41] Blanchard O J. Debt, deficits, and finite horizons[J]. Journal of Political Economy, 1985, 93(2):223-247.

[42] Yaari M E. Uncertain lifetime, life insurance, and the theory of the consumer[J]. Review of Economic Studies, 1965, 32(2):137-150.

[43] 武康平, 倪宣明, 殷俊茹. 浅析人口老龄化对经济发展的影响[J]. 中国人口、资源与环境, 2014, 24(12):103-108.

[44] 武康平, 倪宣明, 殷俊茹. 人口老龄化, 经济增长与社会福利——基于内生经济增长理论的分析[J]. 经济学报, 2015, 2(1):47-60.