需求率受推广努力水平影响的新能源汽车租赁系统协调契约
2018-03-29经有国郭培强秦开大
经有国,郭培强,秦开大
(昆明理工大学管理与经济学院,云南 昆明 650093)
1 引言
进入新世纪以来,随着国家经济实力和人民生活水平的显著提高,汽车已经普遍成为人们日常出行的伐步工具,我国各大城市的汽车保有量也随之逐年激增。然而,随着城市汽车数量和尾气排放的剧增,带来了诸如城市空气加剧恶化、交通日益拥堵等一系列严重问题。对于一个城市而言,大力发展高效的新能源汽车租赁服务业,有利于提高汽车使用效率、改善空气质量以及缓解交通拥堵。
当前新能源汽车租赁市场尚处于成长阶段的培育期,消费者对新能源汽车的购买和使用等方面存有疑虑,因此需要政府出台有效的扶持政策以提高新能源汽车的市场占有率和使用率;新能源汽车相对于传统的交通工具具有替代性,且能降低环境污染成本,间接创造环保效益,因此各级城市政府都在大力推广新能源汽车,并为新能源汽车的购买和使用提供一定额度的补贴政策。由于新能源汽车租赁企业注重自身利益以及政府对环保效益的高度重视,使得政府和租赁企业之间的合作显得顺理成章。
许多学者从不同角度对汽车租赁问题进行了深入研究。在车队配置方面,Kochel和Kunze[1]基于仿真优化方法研究了租赁企业的车队配置和车辆动态调度模型。陈旭[2]通过建立车队配置和定价模型,采用收益管理的思想对汽车租赁企业的最优选择进行了定量研究。Fink和Reiners[3]通过运用最小费用网络流优化模型提升了汽车租赁商的车队利用效率。在此基础之上,George和Xia[4]则从车辆的角度来观察系统,并设计了一个封闭的排队网络模型,从而求解出了汽车租赁公司的最优车队配置。You和Hsieh[5]则在需求不确定的情况下,运用整数规划模型确定了汽车租赁公司的最优车队配置,并且证明了模型的有效性和鲁棒性。在最优决策和收益方面,Wu和Hartman[6]运用Benders分解和拉格朗日松弛思想研究了汽车租赁企业的最优决策问题,并给出了最优运营方案。刘德文和鲁若愚[7]基于粒子群算法研究了短期汽车租赁服务的调度优化问题。Li和Pang[8]则综合考虑了汽车租赁的时间长度以及车队运送的灵活性,并运用动态规划的方法,研究了汽车租赁企业的最大收益。然而,以上文献只是通过运用不同的优化方法使得租赁企业利润最大化,主要针对传统租赁企业进行研究的,并没有考虑新能源汽车对环境的影响以及政府的政策因素。事实上,新能源汽车租赁作为推广新能源汽车的新商业模式,得到了政府和企业的广泛认可与重视,像北京、上海、杭州及昆明众多城市已经开始实施该商业模式,由于该商业模式具有正的外部性以及政府对环保的高度重视,使得政府与租赁企业之间有意愿开展合作,因此本文将主要研究新能源汽车租赁企业和政府之间的合作与协调机制,并通过创新性运用供应链契约理论,使得系统和双方都能实现利益最大化。
在有关需求依赖努力水平的供应链协调契约方面。一些学者从回购契约角度出发,研究了需求受努力水平影响的回购策略,如Krishnan和Kapuscinski[9]、Xing和Liu[10]。Bernstein和Federgruen[11]、Giri和Bardhan[12]、何丽红和廖茜[13]在需求依赖价格和努力水平的情况下,研究了零售商与供应商之间的合作协调机制。此外,曲道钢与郭亚军[14]、胡本勇与陈旭[15]、庞庆华和蒋晖[16]、曹二保和郑健哲等[17]、时茜茜和朱建波等[18]则以收益共享契约为基础,分别研究了需求依赖努力水平情况下的两渠道间收益共享协调契约、收益共享和努力成本共担的协调契约、回馈与惩罚策略的收益共享契约、双渠道供应链的收益共享契约以及最优收益分配机制。以上文献主要研究供应链下零售商的促销努力水平,对本文研究新能源汽车租赁模式下政府的推广努力水平具有一定的借鉴价值。综上所述,本文将推广努力水平纳入决策模型,通过推广努力水平的变化,分析它对新能源汽车租赁企业车队配置的影响,从而更加深入的研究两者的合作与协调机制。
2 问题描述及假设
考虑一个城市范围内由新能源汽车租赁企业和当地政府组成的二级系统。系统中新能源汽车租赁企业与政府的决策行为可用纳什博弈来描述,政府和新能源汽车租赁企业的地位均等,其中政府的目标是追求城市环保效益最大化;新能源汽车租赁企业的目标则是追求自身利润最大化。两者作为相互联系的利益主体,政府可通过提供相应激励政策(如补贴、奖励政策)、向市民宣传推广的方式来影响新能源汽车租赁企业的车队配置和市场需求率,从而影响新能源汽车租赁企业的收益;租赁企业又能够通过调节车队配置的规模对城市的环保效益产生直接的影响。双方为了获取更多的利益,在合作周期内通过相应的合作与协调机制达到互利共赢,并且实现系统整体利益最大化。
事件发生的时序如图1所示:

图1 事件发生的时序图
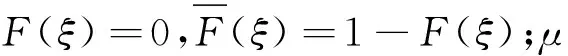
假设1:新能源汽车租赁企业和政府满足理性人、风险中性及信息对称的假设。
假设2:g(e)表示政府推广努力水平为e时的努力成本,随着政府推广努力水平的提高,努力成本也随之增大,为不失一般性,存在g′(e)>0,g″(e)>0,且g(0)=0。
假设3:单位时间内的平均需求率λ(e,ξ)是推广努力水平e与随机变量ξ的函数,两个变量相互独立,设λ(e,ξ)=y(e)+ξ,即平均需求率函数满足推广努力水平与随机变量的加法形式。假设y'(e)>0,为了便于研究,假设y(e)=a+be,a表示市场容量,b表示与推广努力水平相关的需求弹性,即λ(e,ξ)=a+be+ξ。
3 基本决策模型
单位时间内有效出租时间函数τ(λ(e,ξ),q)表示为:
(1)

那么,单位时间内有效出租时间的期望函数E[τ(λ(e,ξ),q)]可表示为:
(2)
3.1 分散决策模型
在分散决策情况下,新能源汽车租赁企业根据自身利益选择最优车队配置,政府也会根据自身的实际情况来确定最优推广努力水平,两者分别以各自利益最大化为前提进行决策。此时新能源汽车租赁企业的期望收益函数为:
πr(q,e)=E{[(p-c1)τ(λ(e,ξ),q)T-c2]q}=
(3)
在城市内部总需求既定的情况下,新能源汽车的使用率越高,所创造的环保效益就越大,因此政府的环保效益与合作周期内q辆新能源汽车行驶的总里程正相关,且取决于出租计费时间τ(λ(e,ξ),q)、单位时间内平均行驶距离d和单位距离所创造的环保效益r。因此政府的期望环保效益函数表示为:
R(τ(λ(e,ξ),q),d,r)=E{τ(λ(e,ξ),q)Tdrq-
(4)
命题1:在分散决策情况下,根据新能源汽车租赁企业的期望收益函数和政府的环保效益函数可得其最优车队配置和推广努力水平同时满足:

证明:在给定推广努力水平e下,由式(3)可求解出πr(q,e)关于q的一阶、二阶导数:
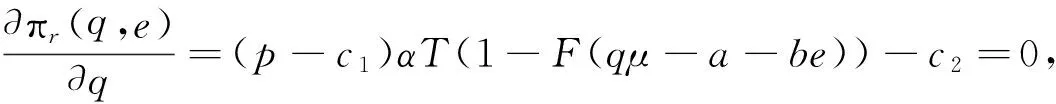
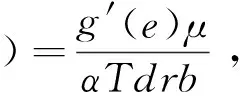
3.2 集中决策模型
在集中决策情况下,新能源汽车租赁企业和政府作为一个整体,共同制定系统的最优车队配置和推广努力水平。下面将统一用上标c来表示集中决策,此时系统期望收益函数为:
πc(q,e)=(p-c1+dr)
(5)
根据式(5)可得总体期望收益函数关于q,e的海赛(Hessian)矩阵:
(6)

对式(5)分别求关于q,e的一阶导数,可得到在集中决策下的最优解(qc,ec)同时满足以下两个等式:
(7)
(8)
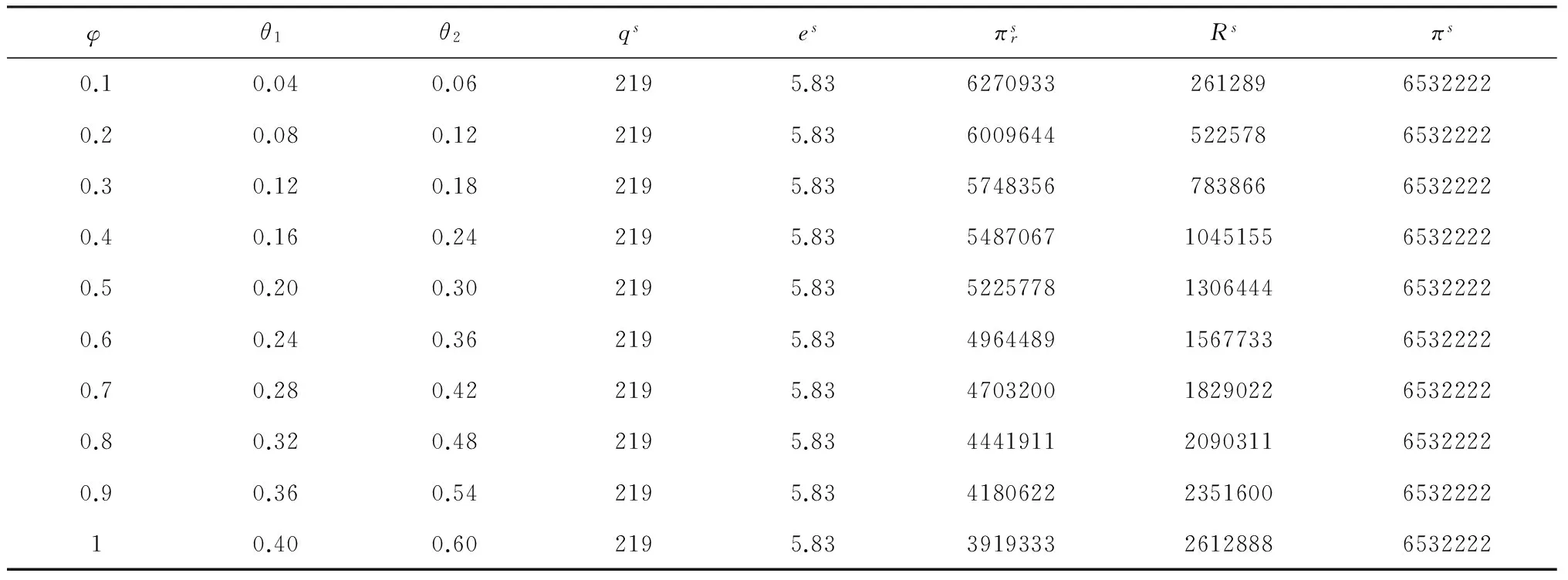
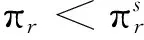
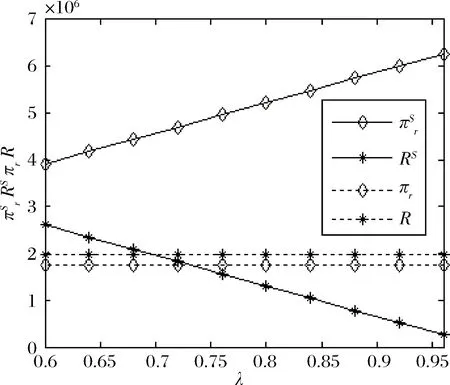
命题2:当e*=ec,则q* 由命题2可知,分散决策时的最优车队配置与最优推广努力水平无法同时等于集中决策时的相应最优决策,因此不能实现系统的协调,故需要进一步研究一种合作与协调机制。 为此,本节提出一种基于收益共享与成本共担的组合契约模型。假设政府将其环保效益的1-φ(0<φ<1)作为激励政策分享给新能源汽车租赁企业,在此基础上政府为新能源汽车租赁企业承担折旧费用的比例为θ1,而新能源汽车租赁企业则为政府承担努力成本的比例为θ2,0<θi<1(i=1,2)。下面将统一用上标s来表示,此时新能源汽车租赁企业和政府的期望收益函数分别如式(9)、(10)所示: (9) Rs(τ(λ(e,ξ),q),d,r)=E{φτ(λ(e,ξ),q)Tdrq-φg(e)-θ1c2q+θ2g(e)} (10) 命题3: 当契约参数{φ,θ1,θ2}满足式(11)、(12): (11) (12) 收益共享与成本共担的组合契约能够实现新能源汽车租赁系统的协调。 证明:为实现系统协调,就要使得协调契约与集中决策下的最优车队配置和推广努力水平相等,即需要同时满足以下两个等式: (13) (14) 命题4:当契约参数{φ,θ1,θ2}满足: (15) 由命题(4)可知,新能源汽车租赁企业和政府的利润分配由λ来决定,一方的讨价还价能力越强,λ越大,获得的利润也会越多;一方的讨价还价能力越弱,情况与之相反。总体而言,系统的总利润维持不变。 出于理性人的考虑,要使协调契约模型具有帕累托改进,必须满足以下条件: 命题5:当收益共享参数φ满足: 基于成本共担的收益共享契约对新能源汽车租赁企业和政府具有帕累托优势。 E{[(p-c1)τ(λ(e,ξ),q)T-(1-θ1)c2]q+ (1-φ)R(τ(λ(e,ξ),q),d,r)-θ2g(e)}≥ E{[(p-c1)τ(λ(e,ξ),q)T-c2]q} (16) 将式(11)、(12)中θ1,θ2分别由φ替换并代入式(16),可得: 令Rs(τ(λ(e,ξ),q),d,r)≥R(τ(λ(e,ξ),q),d,r),由式(10)和式(4)可得式(17): E{φτ(λ(e,ξ),q)Tdrq-φg(e)-θ1c2q+θ2g(e)}≥E{τ(λ(e,ξ),q)Tdrq-g(e)} (17) 将式(11)、(12)中θ1,θ2分别由φ替换并代入式(14),可得: 综上分析,本文所提出的协调契约满足以上条件,该契约能够实现系统协调和帕累托改进。 为了验证以上模型的可行性,下面将进行数值分析进行验证。假设单位时间内的平均需求率λ(e,ξ)=200+100e+ξ,ξ服从均匀分布,即ξ~U(0,400)。T=300天,p=200元/天,μ=5人/天,α=0.6,c1=50元,c2=10000元,d=200公里,r=0.5元/公里,g(e)=10000e2。将以上参数代入基本决策模型进行求解,通过运用MATLAB7.0软件,可以得到以下研究结果: 在分散决策下,根据建立的基本决策模型可计算出此时的最优车队配置q*=128辆,最优推广努力水平e*=3.98,(验证了命题1的正确性)。新能源汽车租赁企业的期望利润πr(q,e)=175万元,政府的期望环保效益R(τ(λ(e,ξ),q),d,r)=199万元,系统的期望利润(收益)π(q,e)=374万元;在集中决策下,由集中决策模型可得系统的最优车队配置qc=219辆,最优推广努力水平ec=5.83,系统的总体期望利润πc(q,e)=653万元;通过具体的算例分析可以看出,分散决策下新能源汽车租赁企业的最优车队配置和推广努力水平都低于集中决策,即q* 在收益共享与成本共担的协调契约模型下,通过调整契约参数{φ,θ1,θ2}的大小来实现系统协调;通过调整λ的大小,来实现利润在新能源汽车租赁企业和政府之间的利益分配。最优决策如表1所示: 表1 协调契约模型下的最优决策 由表1可知,协调契约下的最优车队配置和推广努力水平始终与集中决策下的相等,当0<φ<1时,可求解出成本共担的契约参数的取值范围为:φ=2.5θ1,φ=1.67θ2,满足0<θi<1(i=1,2),说明收益共享与成本共担组合契约可以使利润达到系统最优。(验证了命题3的正确性)。与集中决策相比,无论契约参数如何变化,基于成本共担和收益共享组合契约下的整体利润维持不变,当0.76<φ<1时,新能源汽车租赁企业和政府的利润都大于分散决策下的利润,因此能够实现帕累托改进(验证了命题5的正确性)。 图2 成本共担系数θ2的变化对新能源汽车租赁企业和政府收益的影响 图3 利润分配系数λ的变化对新能源汽车租赁企业和政府收益的影响 由图3可知,新能源汽车租赁企业和政府的利润随着λ的变化而变化,当λ逐渐变大时,新能源汽车租赁企业的利润也随之增大,政府的利润随之减小;当λ逐渐减小时,情况与之相反。其中λ的取值范围为0.6<λ<0.95,在此区间内λ可以对系统的整体利润进行分配,而且总体利润保持不变(验证了命题4的正确性)。 为了满足节能减排、可持续发展的需要,国家已经将新能源汽车定位为战略性新兴产业,并通过政府的扶持政策来促进新能源汽车租赁行业的发展,但是由于当前汽车租赁市场尚处于成长阶段的培养期,探讨新能源汽车租赁具有重要的理论和现实意义。本文在需求不确定且与推广努力水平相关的情况下,分析了新能源汽车租赁企业和政府之间的合作协调机制,并确定了最优车队配置和推广努力水平。研究发现基于成本共担的收益共享契约能够实现系统协调和帕累托改进。需要说明的是,文章假设信息对称且风险中性的,并未考虑信息不对称问题以及决策者的风险偏好问题,因此,在后续的研究中将会对这些问题展开深入的探讨。 [1] Köchel P, Kunze S, Nieländer U. Optimal control of a distributed service system with moving resources: Application to the fleet sizing and allocation problem[J]. International Journal of Production Economics, 2003, 81-82: 443-459. [2] 陈旭. 基于收益管理的汽车出租定价与车辆配置[J]. 系统工程理论与实践, 2005, 03: 264-267. [3] Fink A and Reiners T. Modeling and solving the short term car rental logistics problem[J]. Transportation Research Part E: Logistics and Transportation Review, 2006,42(4): 272-292. [4] George D K and Xia C H. Fleet-sizing and service availability for a vehicle rental system via closed queueing networks [J]. European Journal of Operational Research, 2011,211(1): 198-207. [5] You P and Hsieh Y. A study on the vehicel size and transfer policy for car rental problem[J]. Transportation Research Part E: Logistics and Transportation Review, 2014, 64: 101-121. [6] Wu P L, Hartman J C, Wilson G R. An integrated model and solution approach for fleet sizing with heterogeneous assets[J]. Transportation Science, 2005,39(1): 87-103. [7] 刘德文, 鲁若愚. 基于粒子群算法的短期汽车租赁服务的调度优化问题研究[J]. 管理评论, 2011, 12(2): 166-173. [8] Li D and Pang Z. Dynamic booking control for car rental revenue management: A decomposition approach[J]. European Journal of Operational Research, 2017, 256: 850-867. [9] Krishnan H and Kapuscinski R. Coordinating contracts for decentralized supply chains with retailer promotional effort[J]. Management science, 2004, 50(1): 48-63. [10] Xing D and Liu T. Sales effort free riding and coordination with price match and channel rebate[J]. European Journal of Operational Research. 2012, 219(2): 264-271. [11] Bernstein F and Federgruen A. Coordination mechanisms for supply chains under price and service competition[J]. Manufacturing & Service Operations Management, 2007, 09(3): 242-262. [12] Giri B C and Bardhan S. Coordinating a two-echelon supply chain through different contracts under price and promotional effort-dependent demand[J]. Journal of Systems Science and Systems Engineering. 2013, 22(3): 295-318. [13] 何丽红, 廖茜等. 两层供应链系统最优广告努力水平与直接价格折扣的博弈分析[J]. 中国管理科学,2017,25(2):130-138. [14] 曲道钢, 郭亚军. 分销商需求与其努力相关时混合渠道供应链协调研究[J]. 中国管理科学, 2008, 16(3):89-94. [15] 胡本勇, 陈旭. 考虑努力水平和决策风险偏好的供应链期权销量担保模型[J]. 管理工程学报, 2012, 26(3):184-190. [16] 庞庆华, 蒋晖. 需求受努力因素影响的供应链收益共享契约模型[J]. 系统管理学报, 2013, 22(3):371-378. [17] 曹二保, 郑健哲等. 双渠道供应链应对需求扰动的协调机制研究[J]. 管理学报, 2014, 11(2):267-273. [18] 时茜茜, 朱建波等. 重大工程供应链协同合作利益分配研究[J]. 中国管理科学,2017,25(5):42-51.4 基于收益共享与成本共担的协调契约模型

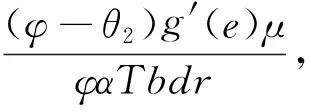
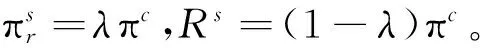
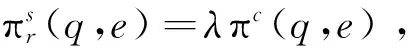


5 算例分析

6 结论
