基于动态因子Copula模型的行业间系统性风险分析
2018-03-29叶五一谭轲祺缪柏其
叶五一,谭轲祺,缪柏其
(中国科学技术大学管理学院,安徽 合肥 230026)
1 引言
经济全球化的疾速发展及金融一体化趋势使得各国金融市场逐渐突破时间和空间的局限,产生了前所未有的相依关联。任何地区的市场局部波动都可能迅速传染到与其相关程度较高的其他地区,造成深远影响,甚至演化成全球性的金融危机。例如,1987年10月19日发生的“黑色星期一”股灾,受到道琼斯工业平均指数暴跌的影响,全球股市也全面下泻,引致全球金融恐慌及随之而来八十年代末的经济衰落;2007年起源于美国住房市场的次贷危机,不仅引发了美国本土股市的剧烈震荡与金融投资的大量损失,随即通过国际贸易体系国际化扩散,也产生了金融蔓延和心理蔓延,给全球其它国家和地区各市场造成了重创。无论是实体经济还是虚拟经济,当面临国际金融危机时,各国市场无法独善其身,严重时会出现多米诺骨牌效应。
次贷危机之后,对系统性风险的识别、测度等方面的研究成为各国学者和政府监管机构共同关注的焦点。传统的风险监管观点侧重于对单个行业机构的风险度量,并假定行业之间风险无溢出效应。而大量金融危机的实例证明,不同于个体风险,系统性金融风险是由单个金融子市场引发,会在不同金融子市场甚至非金融市场之间相互传导,导致整体金融系统不稳定并产生溢出效应的风险[1]。关于金融传染和检验的研究,已有大量的文献。陈九生和周孝华[2]对我国股票市场与ETF市场的风险溢出效应做了研究。Eross等[3]对于银行间市场的流动性风险做出了分析。股票市场行业之间也存在显著的相依关系,关于行业之间相依关系以及在此基础上的系统性风险的分析的文献则相对较少。本文将对上述问题基于动态因子Copula方法进行研究,在此背景下,探析不同行业之间的风险溢出对评估系统性风险大有裨益。
学术界一直尝试采用不同的方法测度系统性风险[4],其中基于市场数据的方法因采用高频数据而受到广大学者推崇。例如,Engle[5]提出DCC-GARCH模型来估计风险传染的时变性。Adrian和Brunnermeier[6]在VaR模型基础上提出了CoVaR方法,具体为给定某一机构遇险条件下,用分位点回归来估计其他机构或市场收益的下位分位点。这是一种“自下而上”的分析方法,用于测度某一金融机构陷入困境后给其它机构带来的风险溢出效应。Acharya等人[7]于2012年提出的边际预期损失法(MES),是“自上而下”的分析方法,通过计算预期损失(ES),反映系统性风险对单个金融机构相对风险变化的敏感程度。这些方法虽然精简,但都有明显不足(例如:CoVaR不能捕捉极端情况下尾部风险;MES无法反映单个机构的风险特质如杠杆程度),这都会造成系统性风险重要信息遗漏。
目前已有学者从同行业公司之间的相依的角度研究某一行业的系统性风险,如宋清华和姜玉东[8]对中国上市银行系统性风险的实证研究。范小云等[9]比较了CoVaR方法与MES方法,并对次贷危机前后我国银行业的系统性风险变化进行了测度。周天芸等[10]以香港银行业为背景,研究了外部冲击之后商业银行系统脆弱性的内生性和传染机理,运用分位数回归方法判定了系统性风险。同时也存在不少分析金融子市场间相互影响的讨论,如沈悦等[11]采用GARCH-Copula-CoVaR模型测度金融四大子市场之间的风险溢出程度。白雪梅和石大龙[12]采用CoVaR法讨论国内金融系统的稳定性,并建立了风险预测模型。曾裕峰等[13]基于非对称MVMQ-CAViaR模型分析了中国金融业不同板块之间风险传导的非对称性。然而较少文献关注市场各行业内部之间系统性风险传导效应,基于时变角度的实证研究则更少。本文的主要目的是结合因子Copula模型和GAS动态模型,处理高维行业间数据,提升系统性风险的估计精度。
为了预测系统性风险,需要得出行业股票收益率的联合分布,但在实际中这很难直接得到,尤其当维数增加时,联合分布的估计更难。当研究高维金融变量时,由于大量参数需要估计,很多学者倾向于使用高斯类方法[12]。然而多元正态分布并不能准确地描述金融变量的特征,因为金融变量的分布大多是非对称的,并且具有厚尾和非对称尾部相依性。为了能够准确地刻画这些特征,通常应用连接边缘分布和联合分布的Copula函数。同时,为了解决高维问题所带来的计算负担,本文采用了因子Copula模型进行实证分析。此外,在相依结构的设定时,借鉴了Dong和Patton[15]的方法,即假定三种形式的相依结构:等相依性、分块相依性和异构相依性。为了得到动态相依结构的估计,本文将基于由Creal等[16]提出的GAS模型,并将其运用到因子Copula中,对行业之间的动态Copula结构进行估计,进而捕捉行业间风险溢出的动态相依性。
因子Copula模型在金融领域已经有了一些应用,但是国内外的文献主要是基于该模型对信用违约互换 (CDS)、债务抵押证券 (CDO) 等进行实证研究,如秦学志和陈田[17],Wu等人[18],没有发现相关文献基于该方法研究市场行业之间的联动效应。因此本文主要有三点贡献:1)创新地结合GAS动态性和因子Copula模型来研究申万一级行业指数间的系统性风险,丰富了当前学者对系统性风险的研究;2) 将因子Copula模型运用于非信用风险的的风险测量上,进一步拓展了该方法的应用范围;3) 新建了系统性风险测量方法——风险预期占比(EPR),可根据模型拟合出的结果得到了28个行业的风险占比,以及与其他行业的关系是否稳定。此外,由于金融行业对于市场经济影响较大,文章将28个行业分为金融行业和非金融行业,并得到了金融行业和非金融行业间的关系。
2 动态因子Copula模型
2.1 Copula函数与条件Copula介绍
Copula函数是把随机变量的联合分布同其边缘分布连接起来的函数,它将单个变量的边缘分布结合成一个多元联合分布,能准确描述变量之间的相依关系[19-20]。
具体来说,对于服从多元累积分布函数F的连续型随机向量具体来说,对于服从多元累积分布函数F的连续型随机向量Y=(Y1,…,Yn)T,Fi为Yi的边缘分布,其中i∈{1,…,n},则必存在一个Copula函数C:[0, 1]n→[0,1],对于所有y=(y1,…,yn)∈n都有F(y)=C{F1(y1),…,Fn(yn)},通常记为Y~F=C(F1,…,Fn)。
因此可以通过N维Copula模型对任意n个随机变量的联合分布进行建模,因为任何一个随机变量都可通过本身的累积分布函数转换成[0,1]上的均匀分布,这一过程通过概率积分变换即可得到。
对于多元时间序列,可以基于条件联合分布,借助于条件Copula来捕捉其相依模式。Patton[20]和Silva Filho等[21]曾对其进行研究。条件Sklar定理如下:


(1)

2.2 因子Copula模型
就金融市场的随机性与资产多样性而言,高维度的联合分布很难确定,参数的估计也是任务繁重,因此高维数据分析的关键是对模型进行维数缩减。在金融领域中,常用的方法是因子分析,它可用于分析资产收益与公共因子之间的相关结构[22]。为了得到多个时间序列的联合分布,Dong和Patton[23]提出用因子Copula模型,可将高维问题转化为若干低维问题来处理。对于n个时间序列或者变量的单因子Copula模型结构如下:
Xit=λit(γλ)Zt+εit,i=1,2,…,n
(2)
其中Zt~Fzt(γz),εit~Fεt(γε),Zt⊥εi∀i。Fzt(γz)和Fεt(γε)分别是公共因子Zt和非公共因子εit的分布函数,λit是公共因子在t时刻的因子负荷(权重)。Xt=(X1t,…,Xnt)是潜在因子变量,它的Copula函数Ct(γ)与观测变量Yt的Copula相同。Xt的条件联合分布可通过Sklar定理应用分解为条件边缘分布和条件Copula:
Xt~Ht=Ct(F1t(γ),…,Fnt(γ);γ)
(3)
在(2)式中,可通过公共因子负荷λit随时间变化来分析因子Copula模型的动态性,也可由公共因子分布Fzt和非公共因子分布Fεt的时变性来产生动态。例如,固定Fzt和Fεt,因子负荷λit增加,就说明变量之间的整体相依水平增加。在文章2.3部分将会描述如何模拟这些动态性。
2.3 广义自回归得分 (GAS) 动态模型
为了研究Copula相依参数可能随时间变化,Patton和Irving[24]提出新的时变Copula。对于高维的情况,可采用GAS模型[16,25]来描述因子Copula的时间动态性。对于一个含有时变参数δt,常量参数γ的Copula,有

δt=ω+Bδt-1+Ast-1
(18)
st-1=St-1t-1
其中St是刻度矩阵 (如Hessian矩阵的逆或它的平方根)。
为了简化模型,这里设定公共因子变量和非公共因子变量的参数形态是恒定的,即γz和γz不随时间变化。同时,假定FZ为自由度参数为νz,非对称参数为ψz的偏t分布,Fε为标准t分布。把(18)式GAS结构应用于(2)式的因子负荷中,简化的模型如下:
logλit=ωi+βlogλi,t-1+αsi,t-1,i=1,2,…,n
(19)
其中si,t=∂logc(ut;λt,γz,γε)/∂logλit,λt=[λ1t,…,λnt]′,γλ=[ωi,β,α]′,ωi是n维的。负荷因子取对数后,权重为正,在实证应用中结果更好。
模型中有n+2个参数需要估计。当n很大时,会产生巨大的计算负担。由此,Dong和Patton[26]基于λt为严格平稳序列的假设,提出了减少待估参数的“方差针对法”。同时结合Creal等对GAS模型的研究所得Et-1[si,t]=0,可推出:
E[logλit]=ωi+βE[logλi,t-1]=ωi/(1-β)
(20)
因此ωi=E[logλit](1-β),则(19)式可改写成(21)式,以便根据观测数据来估计E[logλit],减少待估参数个数。
logλit=E[logλit](1-β)+βlogλi,t-1+αsi,t-1
(21)
假定ρt,X为观测值Xt的秩相关系数向量,则logλt为关于ρt,X的线性函数。相关系数为:
(22)
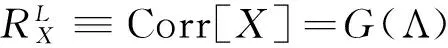
H(ρX)=argmin(vech{φ(G(expa))}-
ρX)′(vech{φ(G(expa))}-ρX)
(23)
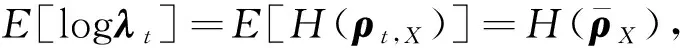

(24)
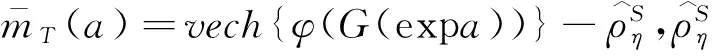
2.4 相依结构类型的设定
随着时间序列的个数增加,模型需要估计的参数也相应增加,这给优化过程带来了更多复杂性。Dong和Patton[26]提出了三种不同的相依结构来达到缩减模型参数个数同时保持模型灵活性的平衡。
考虑(19)中的限制条件,若使ωi=ω∀i,则每组变量间的相依性将会一致,形成等相依结构。这种情况下,只需要估计6个参数,将大大减少模型估计的计算负担。但是等相依结构模型灵活性差,它假设所有的时间序列是同等力度相互依赖的,即对所有序列都是单一的因子负荷,这多少有些过于严格。最灵活的是异构相依结构,它使每个时间序列的因子负荷和其他时间序列的负荷相互独立。这种结构有很多参数,随着时间序列增加,可能增加计算负担。另一种的是Engle和Kelly[27]提出的分块等相依结构,利用事前信息根据相依性对时间序列进行分组,同组中的时间序列有相同的相依关系,只在组内具有同质性。
因此,因子Copula模型可写成如下形式:
Xit=λg(i),t(γλ)Zt+εit,i=1,2,…,n
(25)
logλg,t=ωg+βlogλg,t-1+αsg,t-1
g(i)∈{1,2,…,G}是第i个变量所在的组,G是所分组的个数。当G=1时为等相依结构;当G=n时为异构相依结构;当1 本文选取申万28个一级行业指数日数据进行实证分析,区间为2006年1月4日至2016年7月1日,每个时间序列对应有2550个观测值。数据来源于WIND数据库。28个行业包括:农林牧渔、采掘、化工、黑色金属、有色金属、电子元器件、家用电器、食品饮料、纺织服装、轻工制造、医药生物、公用事业、交通运输、房地产、商业贸易、餐饮旅游、综合、建筑材料、建筑装饰、电气设备、国防军工、计算机、传媒、通信、银行和非银金融。 表1给出了28个行业两两间相关系数的基本统计量。从表中可以看出28个行业间相关系数较大,各行业间存在较强的相依性。 表1 相关系数的基本统计量 图1 等权重组合收益率 图2 市值加权组合收益率 为了对28个行业收益率有一个初步的了解,表2给出了28个行业等权重收益率的基本统计信息。每一行是对收益率基本统计量的描述,例如第一行的均值为28个行业收益率时间序列的均值。如果按列分析,则能找到更详细的描述,如均值的均值、均值的最小值等。值得注意的是,股价对数收益率的偏度均为负数(偏度最大值为-0.0290),呈现出左偏的非对称性;峰度均大于3(峰度最小值为4.5168,标准正态分布峰度为3),因此行业收益率分布呈现明显的“尖峰厚尾”性,显著异于正态分布。 表2 收益率的基本统计量 在建造因子Copula模型前,首先需要将收益率数据通过经验分布变换成均匀分布数据,即估计各行业股票指数收益率的边缘分布。在进行边缘分布估计前,本文采用ADF检验对各收益率序列进行了单位根检验,结果表明各序列皆是平稳序列。 从上面分析可知,传统的模型并不能很好地描述具有尖峰厚尾特征、异方差以及非对称性的收益率数据, 因此需要应用合适的模型来对数据进行建模。自Engle[28]于1982年提出了ARCH模型来分析时间序列异方差性后,Bollerslev[29]在其基础上又提出了GARCH模型,该模型能够很好地处理金融收益率序列的异方差等特性。对于每一个收益率序列,用ARMA(1,0)-GARCH(1,1)来做拟合,模型设定如下: Yit=φ0i+φ1iYit-1+εit,i=1,2,…,28 εit=σitηit 其中,ηit~i.i.d.(0,1)是标准化残差。通常假定ηit服从标准正态分布,但考虑到金融时间序列具有尖峰厚尾性和波动聚集性,标准化残差的边缘分布本文中假定在t-1期信息集下服从均值为0,方差为1的广义误差分布(GED,Generalized Error Distribution),ηit|Fit-1~GED(γi)。当参数γi<2时,GED比正态分布(γi=2)有更厚的尾部。表3中给出了28个行业GARCH模型的参数估计。 表3 GARCH模型的参数估计 续表3 GARCH模型的参数估计 注:表中给出了28个行业的股票指数在样本区间内的边缘分布参数估计结果。***、**、*和·分别表示在0.1%、1%、5%和10%的水平下显著。 表4 各参数的描述性统计量 从表3中可以看出,几乎所有参数估计在0.1%水平和1%水平下都是显著的。28个行业股指的φ0值均接近于零,这表明所研究的各行业的长期收益都趋于零。除此之外,参数α和β值在各行业间相差不大,且α+β<1且接近1,说明这些指数收益率具有积聚效应和较强持续性;另外,所有行业股指收益率GARCH模型中误差项GED分布的参数γ的估计值均小于2,再一次说明了股票市场的收益率确实有尖峰厚尾的特点。基于GARCH模型建立了行业收益率的边际分布以后,下一步将对行业之间的相依结构进行分析。 在对一级行业分类的过程中,投资人可以根据自己的经验定性对行业进行分类,但是这具有一定的主观性。本文基于聚类分析方法对行业进行了分类,并根据经验对一些明显不恰当的分组做出了适当的调整,将28个一级行业均匀分成了7组。行业名称与具体的分组情况如表5所示。 表5 行业及分组 图2给出了7组两两之间的动态60天滚动窗口秩相关系数图,反映了各分组之间的相关程度。对角线上的7个图代表同组间不同行业相关系数的平均值;非对角线上的图代表不同组间不同行业相关系数的平均值。如:第一行第一列的图代表化学工业组内各行业相关系数的平均值;第一行第二列的图代表化学工业与电子与电器两个分组间不同行业相关系数的平均值。可以看出,各行业间均存在不同程度的相依关系。如:电子与电器类和新兴产业之间的相关系数非常显著。这是由于电子行业分组中包括电子元器件,家用电器等一级行业,而新兴行业中包括计算机、通信等行业。21世纪进入互联网时代,高速信息传递成为了社会生活的常态,而这些都是以计算机和通信行业这些新兴行业为基础。计算机和通信行业都是电子元器件的下游行业,电子元器件被广泛应用于各类电子设备,如计算机、通信设备、消费类电子产品中。可以说这两类行业联系的极为紧密,所以电子行业与新兴行业之间存在较高的相关性。 下面将基于因子Copula模型对行业做分块相依性研究。为了便于分析,我们初始假设νz=ν∈,同时在对自由度参数ν做估计时,选用其倒数形式,这样利于避免出现待估自由度参数ν趋于正无穷的情况。关于参数初值的选择,在等相依结构模型中,初始选择ω=0,α=0.05,β=0.95,ν=10,φ=0.1;在分块相依模型中,设定ω1=-0.03,ω7=0.03,在此区间内等间距的取ω2~ω6的值;在异构相依模型中,则类似设定ω1=-0.03,ω28=0.03,并在此区间内等间距的定义ω2~ω27的值。给定初值以后,通过极大似然估计方法可以得到动态因子Copula中各参数的估计值,三种相依结构下的参数估计值如表6所示。 由表6中各相依结构下的AIC值可知,数据拟合最好的相依结构是异构相依,即使在这种结构下有许多惩罚参数。从表5可以看出,对于三种相依结构,β的估计值都非常接近于1(尤其是在异构相依结构下参数估计值β=0.9685),因此,时变参数都表现出很强的短期持续性。ω值代表某一时刻因子负荷的演进过程的截距,因子负荷代表1个行业与其他27个行业的相依性,所以ω的大小在一定程度上代表某一行业在某一时刻受其他行业之间相依性的大小。由异构相依得到的ω值可以得出,化工行业对应的ω值最大,因此与其他行业有着最强的相依关系。化工行业是一个关联性很强的行业,涵盖非常广泛,对于食品、纺织、汽车等行业都需要化工原料的产出与加工,与其他行业的联系也非常的紧密。而且化工产业生产布局较为分散,产品结构与市场需求不匹配,导致化工产业与其他行业的关系非常紧密。 图3 60天滚动窗口秩相关系数图 参数估计值参数估计值ω0.01551/ν∈0.3373α0.0128φ-0.1321β0.9422LL4163.071/νz0.1388AIC-3.2617 分块相依结构 异构相依结构 续表 异构相依结构 下面对Copula的因子负荷参数(λt)进行分析,图4给出了在等相依结构下,动态偏t-t因子Copula的因子负荷(λt)的变化图。可以看出,λt变化范围大多在2.5到2.7之间,并且在2009年中,因子负荷达到峰值。 图5则给出了,异构相依情况下,动态因子负荷(λit)估计值变化趋势。因子负荷(λit)代表了t时刻变量i与其他变量之间的整体相依水平。为了表述更为清晰,这里只选取了农林牧渔、采掘、医药生物、餐饮旅游、汽车与银行业的因子负荷变化图进行展示。可以看出,医药生物业的因子负荷值整体最高,在2012年年初峰值接近4.9,说明医药生物业较样本内其他行业来说受公共因子影响最大。其次是农林牧渔业和采掘业,因子负荷值在4.5左右徘徊。汽车行业因子负荷值最低,区间内最大值仅约3.6,说明汽车行业较样本内其他行业而言,受公共因子的影响最小。 图4 等相依结构下因子负荷(λt)变化图 图5 异构相依下因子负荷(λt)变化图 根据上文介绍的动态因子Copula模型及估计结果,可以对系统性风险进行估计。在估计Copula参数时,首先需要得到个行业指数收益率的边际分布,即将原数据转换为均匀分布数据。本文以均匀分布数据中各行业均值的5%分位点值(约0.0543)作为风险阈值,定义行业未来一年(取250天)超过这一阈值的风险为Ri,t+250=1{Ci,t+250>0.0543},Ci,t+250是实证中所用的均匀分布数据。随后,可以定义测量方法EPR (Expected proportion of industries at risk) 为风险预期占比。给定某一行业i,可以计算出其他行业的EPR。 式中选取每个行业权重相等,EPR值最小可取1/n,最大可取1。这种测量方法本质上与Adrian和Brunnermeier所提出的CoVaR方法相似,都是考虑了个体对市场整体风险溢出的情况。 作为示例,我们给出了在给定农林牧渔业处于风险的条件下,其它行业处于风险预期占比的估计结果,如图6所示,给出了不同时间风险测量(EPR)结果的均值,25%和75%分位点图像。可以观察到,整体EPR均值有起伏但变动不大,最低达到约18%,最高达到约26%。这说明农林渔牧业处于风险对其它行业确有影响,影响比例大概在22%附近。可以按照相同的方法,类似地给出单个行业对其他行业的影响。 图6 农林牧渔业的风险预期占比EPR 以单个行业为出发点研究其对整体行业影响可为风险溢出提供参考依据,但无法准确反映不同行业间的相互影响。2008年金融危机使全球市场经济整体走低,可见金融行业对于市场经济有着非常大的影响,因此研究金融行业与非金融行业间的关系对于行业的风险规避是十分有必要的。已有众多学者对金融行业间的风险溢出效应进行了深入的研究,本文则将重点放在金融行业对非金融行业风险影响、非金融行业对金融行业的风险影响以及非金融行业对其它非金融行业风险影响三个方面上。 本文研究的28个样本行业包括了2个金融行业(银行和非银金融)和26个非金融行业,将行业分为金融行业和非金融行业两大分类后,可以得出下面的EPR图。图6中有三条时间序列线,可以清晰地观察到同类别行业之间以及不同类别行业间的溢出影响。从动态走势来看,有如下的几个特点。 总体来说,非金融行业间的风险影响占比(虚线)在三种情况中较高,在2007年、2013年至2015年间有较明显起伏。下面将结合实际情况对数据结果进行推测说明。以钢铁行业为例,我国作为世界上最大的钢材生产和出口国,在对外出口上受到制约。2008年钢材出口4184万吨,同比减少325万吨,下降7.2%,在国内汽车、造船业均不景气的情形下,国内钢材需求量也急剧下滑,房地产、汽车等行业均进入低谷期。有色金属价格暴跌,居民压缩非必需性的消费,纺织业、食品制造业、电器设备等行业都遭遇风险。由此可解释非金融行业间也存在较高的风险溢出,风险溢出曲线变化可以为行业投资提供指导。 从非金融行业对金融行业风险溢出曲线(红线)中可以看出,非金融行业对金融行业的影响一直处在不稳定的状态。结合实际进行分析,在2007年至2010年和2013年至2015年年间,震动较剧烈。2007年美国次贷危机使市场流动性下降,阻碍了各行各业生产增长,同时大大限制了中国的出口,对经济造成严重负面影响。作为世界出口大国,国内汽车、纺织等行业产量的下降导致经济受到沉重打击,进而抑制了金融行业发展,这必然会导致非金融行业与金融行业关系一直处于不稳定状态。 反观金融行业对非金融行业的影响,风险溢出曲线一直处于较平稳且较大的状态,说明金融行业对其他行业的影响较为显著且平稳。下面将以非金融行业中的钢铁业为例来分析金融行业对于非金融行业的影响,钢铁业和银行业之间一直处于微妙的平衡关系。钢铁业一直是产能过剩的重灾区,有着高产能、高成本、低价格、低效益的特点。从上游的采掘到下游的销售,风险最大的是钢贸信贷部分,一旦资金链出问题将迅速致使企业倒闭,银行大面积抽贷也会对其本身带来巨大的损失。类似于银行业与黑色金属业风险关联平衡,其它行业也处在类似的情形中。所以非金融行业对金融行业对风险影响一直处于较高且平稳的状态,预期风险占比保持在20%至25%之间。 图7 金融行业与非金融行业的风险溢出EPR 为了研究中国股市行业之间的动态相关关系以及系统性风险溢出变化趋势,本文取申万28个一级行业2006年1月4日至2016年7月1日的28个行业指数日数据,从动态的角度基于因子Copula模型,实证研究了行业日收益率指数的动态相关性,其中在实证时将GAS分为等相依、分块相依、异构相依三种结构进行了比较分析。首先对于单个行业与其他行业间的相关性做出了分析。化工行业与其他行业的关系动荡较大,ω值达到0.0336,最为不稳定。医药生物行业受其他行业影响,因子负荷值整体最高,在2012年年初峰值接近4.9;汽车行业因子负荷值最低,区间内最大值仅约3.6,较样本内其他行业而言受公共因子的影响最小。在对动态因子Copula模估计的基础上,通过定义风险预期占比(EPR)可以对行业间的系统性风险溢出进行度量。实证结果表明,三种情况风险溢出效应皆十分显著,其种非金融行业间的EPR相对最高,非金融行业对金融行业风险溢出影响不稳定,而金融行业对非金融行业的风险影响一直处于较平稳且较大的状态。由于金融行业的特殊地位,同时考虑到2008年金融危机对全球经济的冲击,衡量金融行业对其他行业间的风险溢出效应是非常必要的。金融行业对于非金融行业的影响处在较为平稳且影响较大的状态,非金融行业间的风险占相对高,非金融行业对于金融行业的影响则处在较不稳定的状态。对于投资者和金融风险管理者来说,行业之间的风险溢出效应研究至关重要。只有把握行业间动态相互影响程度以及行业间风险占比,才能对于行业的风险做出准确且及时的预测,进而更好的做出投资决策。 [1] 张晓朴. 系统性金融风险研究:演进、成因与监管[J]. 金融监管, 2010,(7): 58-67. [2] 陈九生, 周孝华,. 基于单因子MSV-CoVaR模型的金融市场风险溢出度量研究[J]. 中国管理科学, 2017,25(1): 21-26. [3] Eross A, Urquhart A, Wolfe S. Liquidity risk contagion in the interbank market[J]. Journal of International Financial Markets, Institutions and Money, 2016,45: 142-155. [4] Schwaab B.New quantitative measures of systemic risk[M]. Financial Stability Review Special Feature E, European Central Bank, 2010: 147-153. [5] Engle R. Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models[J]. Journals of Business & Economic Statistics, 2002,20(3): 339-350. [6] Adrian T, Brunnermeier M K. CoVaR Staff Report 348[J]. Federal Reserve Bank of New York, 2009. [7] Acharya V, Pedersen L H, Philippon T, et al. Measuring systemic risk[J]. The Review of Financial Studies, 2017, 30(1):2-47. [8] 宋清华,姜玉东. 中国上市银行系统性风险度量[J]. 财经理论与实践,2014,35(192):1-3. [9] 范小云,王道平,方意. 我国金融机构的系统性风险贡献测度与监管——基于边际风险贡献与杠杆率的研究[J]. 南开经济研究, 2011,(4): 3-20. [10] 周天芸,周开国,黄亮. 机构集聚、风险传染与香港银行的系统性风险[J]. 国际金融研究, 2012,(4): 77-87. [11] 沈悦,戴士伟,罗希. 中国金融业系统性风险溢出效应测度基于GARCH-Copula-CoVaR模型的研究[J]. 当代经济科学, 2014,36(6): 30-38. [12] 白雪梅,石大龙. 中国金融体系的系统性风险度量[J]. 国际金融研究, 2014,(6): 75-85. [13] 曾裕峰, 简志宏, 彭伟. 中国金融业不同板块间风险传导的非对称性研究——基于非对称MVMQ-CAViaR模型的实证分析[J]. 中国管理科学, 2017,25(8): 58-67. [14] Bradley B O, Taqqu M S. Financial risk and heavy tails[K]. In: Handbook of Heavy Tailed Distributions in Finance. Elsevier, 2003: 27-33. [15] Dong H O, Patton A J. Time-varying systemic risk: Evidence from a dynamic copula model of CDS spreads[J]. Journal of Business & Economic Statistics, 2017: 1-15. [16] Creal D D, Koopman S J, Lucas A. Generalized autoregressive score models with applications[J]. Journal of Applied Econometrics, 2013, 28(5): 777-795. [17] 陈田,秦学志. 债务抵押债券CDO定价模型研究综述[J]. 管理学报, 2008, 5(4):616-624. [18] Wu P C, Kao L J, Lee C F. Factor copula for defaultable basket credit derivatives[M]. New York: Springer New York, 2015: 639-655. [19] Patton A J. A review of Copula models for economic time series[J]. Journal of Multivariate Analysis, 2012, 110(2012): 4-18. [20] Patton A J. Modeling asymmetric exchange rate dependence[J]. International Economic Review, 2006, 2(47): 527-556. [21] Silva Filho O C, Ziegelmann F A. Assessing some stylized facts about financial market indexes: A Markov Copula approach[J].Journal of Economic Studies, 2014, 41(2): 253-271. [22] 陈志平,宋振霞. Copula函数在多因子模型系数估计中的应用[J]. 系统工程理论与实践, 2013, 33(10): 2471-2473. [23] Dong H O, Patton A J. Modelling dependence in high dimensions with factor copulas[R]. working paper, Duke University, 2012: 4-5. [24] Patton A J, Irving D L S. Dynamic Copula models and high frequency data[J]. Journal of Empirical Finance, 2015, 30(1): 120-135. [25] Blasques F, Koopman S J, Lucas A. Specified generalized autoregressive score models: Feedback effects, contraction conditions and asymptotic properties [R]. Tinbergen Institute Discussion Paper, 2014, 74(3). [26] Dong H O, Patton A J. Time-varying systemic risk: Evidence from a dynamic copula model of CDS spreads[R]. Working paper, Economic Research Initiatives at Duke, 2013: 28-30. [27] Engle R F, Kelly B. Dynamic equicorrelation[J]. Journal of Business and Economic Statistics, 2012, 30(2): 212-228. [28] Engle R F. Autoregressive Conditional Heteroskedasticity with Estimates of the Variance of UK Inflation[J]. Econometrica, 1982, 50(4): 987-1007. [29] Bollerslev T. Generalized autoregressive conditional Heteroskedasticity[J], Journal of Econometrics, 1986, 31(3): 307-327.3 实证分析
3.1 数据描述与预处理

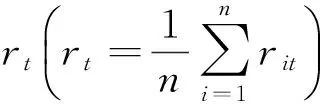
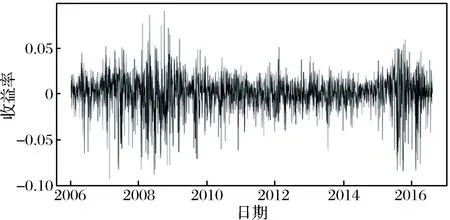


3.2 边缘分布估计
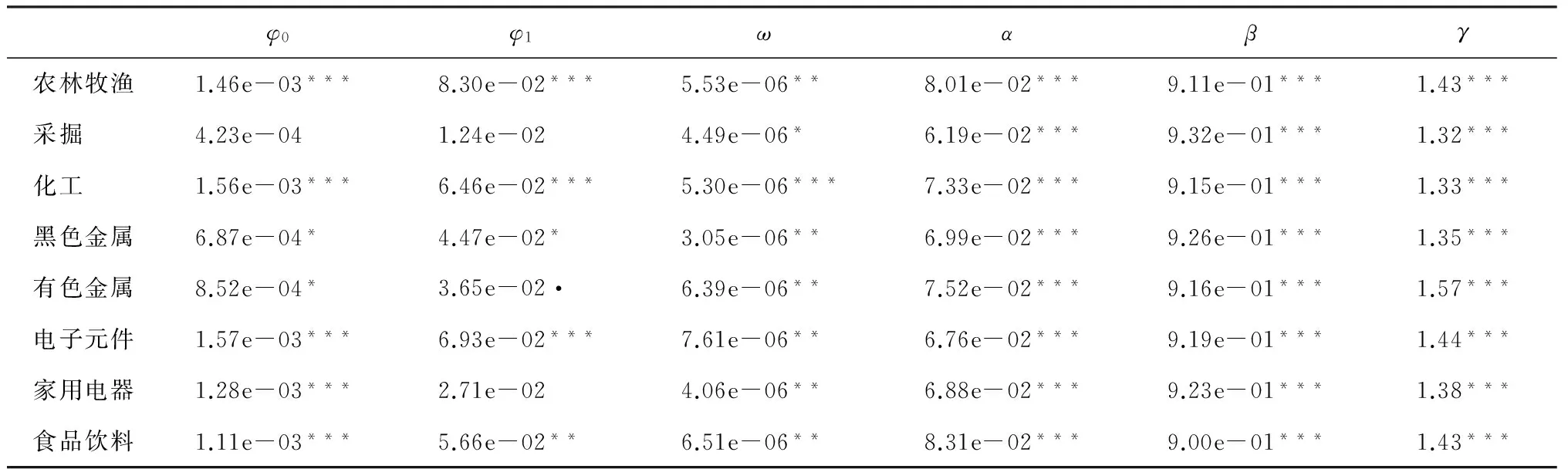
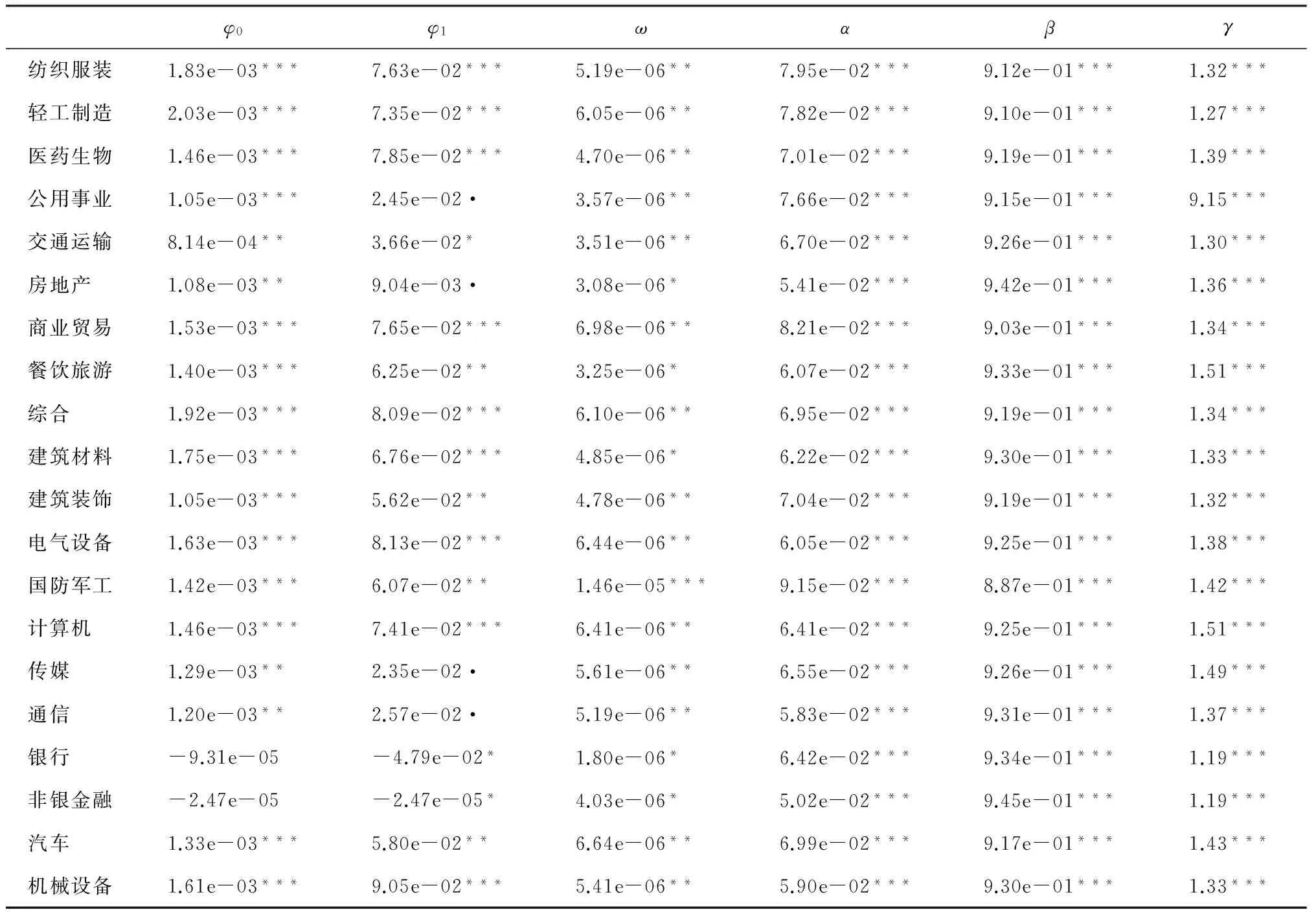

3.3 动态因子Copula分块相依研究
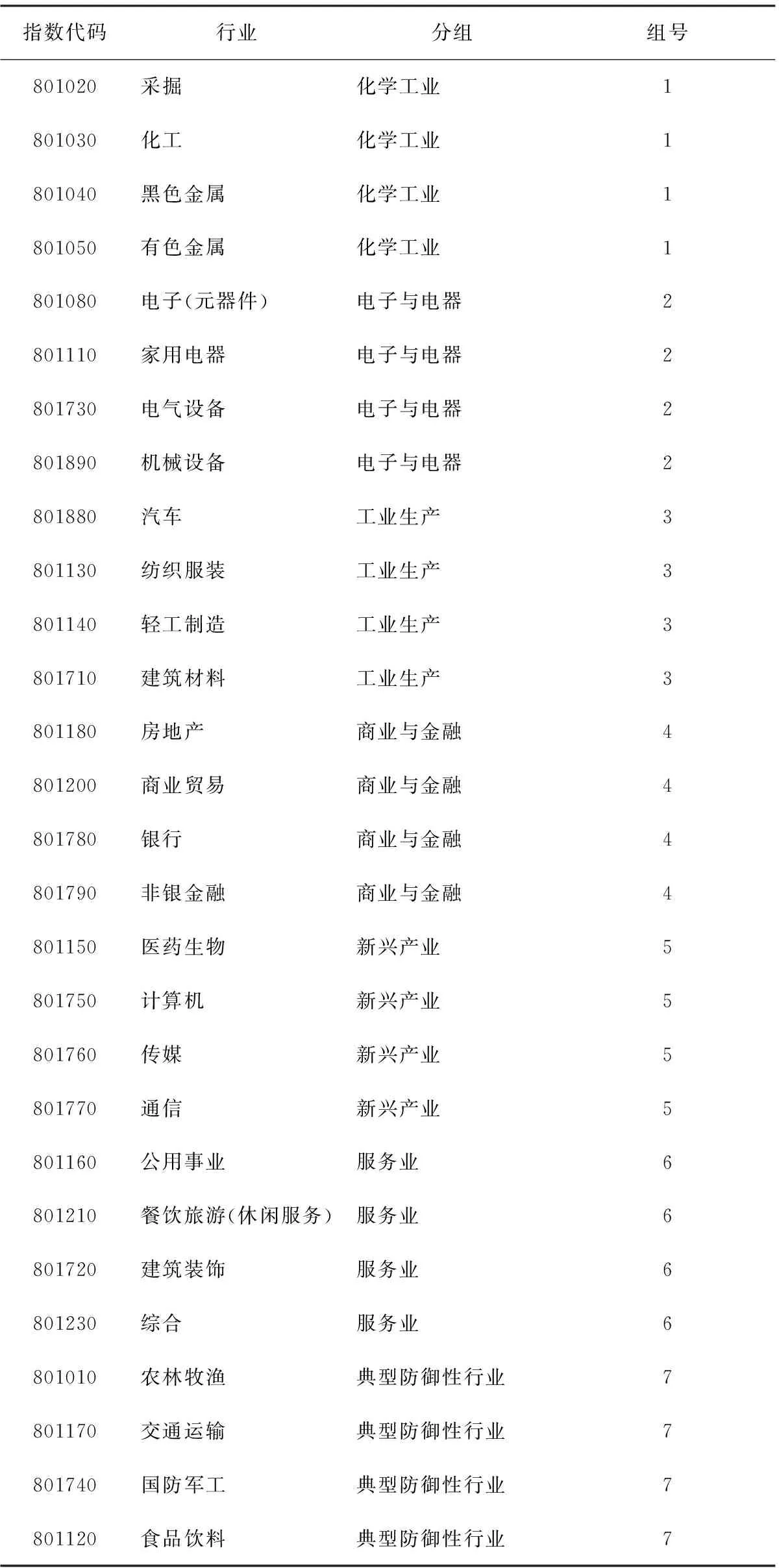


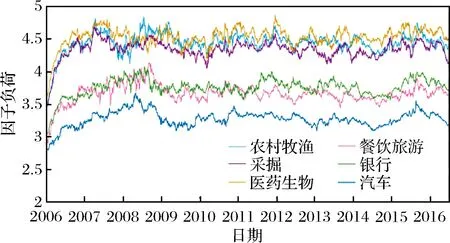
3.4 风险预期占比

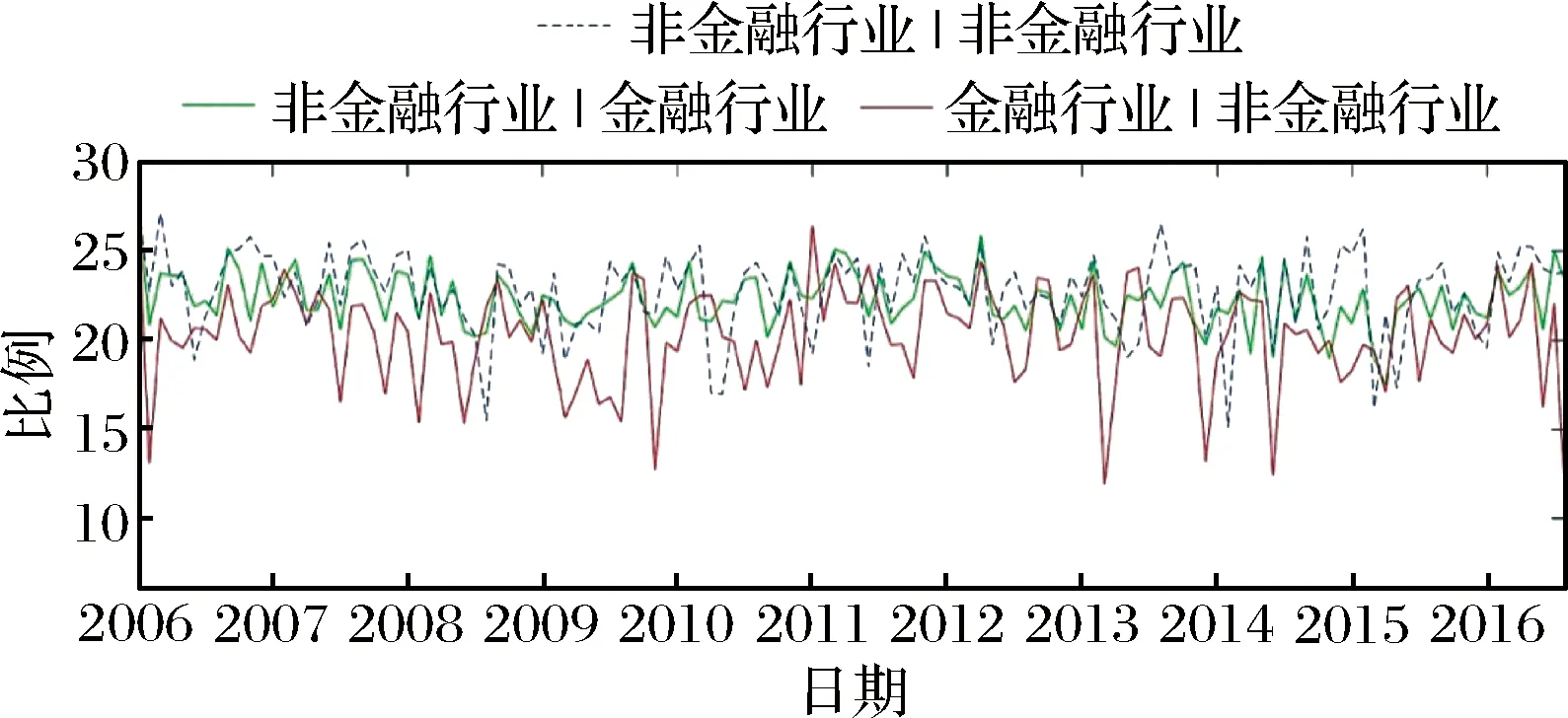
4 结语
