三级装备制造业供应链质量管理行为研究

2018-03-29孙健慧张海波赵黎明

中国管理科学 2018年3期

孙健慧，张海波，赵黎明

(1.天津商业大学会计学院，天津 300134；2.北京师范大学经济与管理学院，北京 100875； 3.天津大学管理与经济学部，天津 300072)

1 引言

作为我国独有的专业名词，装备制造业是指为国民经济和国家安全提供各种生产技术类装备的工业的总称，具有资本、技术和劳动密集等特性。装备制造业是我国制造业的重要组成部分，肩负着我国工业发展和国防建设的重要使命。经济一体化背景下，我国对外开放的程度不断加深，装备制造企业之间的市场竞争也日趋激烈，当前企业所面临的竞争已扩展到企业所在供应链之间的竞争。这其中，产品质量作为装备制造企业的立足之本，能够有效提高企业的核心竞争力，增加企业经济效益。在供应链中，产品的生产工艺流程决定了最终的产品质量不仅取决于制造商的质量管理，还有赖于供应商的质量控制。因此，产品质量突破了单个企业的边界，供应链上任一环节的质量问题都会造成产品的质量隐患，如2009年丰田汽车召回门事件就是由于供应商提供了不合格的配件。可见，供应链环境下，装备制造企业的产品质量不仅依赖于企业内部的质量管理，还需要供应链上下游企业的共同参与[1]。因而，基于供应链视角研究装备制造企业质量管理行为是解决产品质量问题、赢得供应链竞争优势的有效途径。

目前，供应链质量管理作为供应链运营的关键问题，受到国内外学者的普遍关注。Kaynak等[2]通过实证检验明确了质量管理实践对供应链绩效提升的重要意义。Kuei等[3]在传统供应链管理的基础上提出了供应链质量管理的研究框架。Cachon等[4]考察了供应链成员产品质量决策中，收入共享契约相较于其他契约的优势和局限性。Handley等[5]重点考察了供应链业务外包过程中的质量管理活动，阐述了契约激励和监测机制的效用机理。Chao等[6]设计了道德风险下制造商和供应商的契约形式和合同菜单，以推动产品质量改进。Hsieh等[7]探讨了信息不对称条件下制造商和供应商的质量投入和检验策略。Xie Gang等[8]研究了需求不确定情形下供应商和制造商的质量决策问题，进而基于制造商主导和供应商主导两种情形考察了质量改进策略的实施效果[9]。Shi Hongyan等[10]探讨了基于消费者异质性的不同分销渠道下供应链成员的产品质量决策问题。El Ouardighi等[11]考察了二级供应链在不同契约类型下的质量改进情况。Liu Weihua等[12]研究了二级供应链中供应商和制造商的质量控制问题。Giri等[13]探讨了不同质量条件下供应商和制造商的均衡决策问题。Liu Guowei等[14]重点分析了二级供应链中制造商的短视行为对产品质量的影响。

国内学者也对此类问题进行了分析与探讨。周明等[15]探讨了不同委托代理模型下供应商和制造商的质量合同设计问题。但斌等[16]研究了二级供应链管理中的产品质量决策问题。蒲国利等[17]通过对国内外关于供应链质量管理文献的梳理和总结，提出了学科的发展方向。胡军等[18]通过引入收益共享、奖励惩罚和特许经营契约研究了二级供应链质量管理的协调机制。夏兆敏等[19]重点分析了二级猪肉供应链中企业质量行为的协调问题。于荣等[20]采取蜈蚣博弈方法考察了食品供应链质量管理中的多主体合作问题。朱立龙等[21]分析了两级供应链产品质量控制的契约模型，进而考察了非对称信息条件下产品质量的控制策略[22]。申强等[23]讨论了道德风险下制造商和供应商的质量控制与协调机制。石丹等[24]分析了契约治理和关系治理在供应链质量管理中的应用。刘威延等[25]探究了由不完全信息转化为完全信息时，供应商和生产商的质量合同设计问题。古川等[26]重点考察了消费者质量识别对于供应链成员质量管理决策的影响。马鹏等[27]探究了不同公平偏好行为下制造商和零售商的质量投资策略问题。高鹏等[28]分析了不同市场领导结构下二级供应链的质量决策问题。洪江涛等[29]运用微分博弈方法研究了两级供应链质量管理过程中博弈结构对均衡结果的影响。刘云志等[30]考察了基于损失规避与产品质量的二级供应链协调问题，研究了不同情形下供应链成员的行为策略。

综上可见，国内外学者对一般供应链的质量管理问题做了较多研究，但对于装备制造业供应链的质量管理行为研究较少。且现有关于供应链质量管理问题的研究大多基于单期时间的静态博弈分析，忽视了质量形成的长期性、复杂性和动态性特点，少量着眼于动态框架的文献也仅仅是对制造商和供应商组成的二级供应链进行研究。但现实中，由于装备制造业的生产工艺更为精细，生成流程更为复杂，生产所需原材料更为繁多，简单的二级供应链已不能满足其生产需求，也不符合现实情况，需要更多上下游企业间的分工合作，因而供应链层级也就更多，一般为三级。根据装备制造业供应链的现实特点，通常是将供应商进一步细分为部件供应商与零件供应商。其中，零件供应商是负责装备最小组成部分——零件生产的企业，部件供应商是负责利用零件供应商提供的零件，进一步生产更高级别的产品单元——部件的企业。如我国轨道交通装备制造业的产品——高速列车，由中国中车组装生产(制造商)；而列车所需的基础制动装置(部件)则是由下一级供应商——克诺尔公司(部件供应商)提供；进而，基础制动装置中的核心材料如制动盘、夹钳、闸片、电机、变压器、齿轮箱等等(零件)，又是由再下一级的供应商(零件供应商)提供给克诺尔公司的。

鉴于此，本文将装备制造业的质量管理问题作为研究对象，考虑时间效应的影响，基于装备制造业的现实特点，构建三级装备制造业供应链质量管理的微分博弈模型，研究制造商、部件供应商和零件供应商在不同博弈情形下的最优质量管理行为、最优收益及供应链的整体收益状况，探究装备制造业供应链产品质量的影响因素，分析供应链合作质量管理行为的协调机制，以期对装备制造业产品质量的提升和供应链整体收益的增加提供科学指导。

2 模型构建

2.1 问题描述

装备制造业供应链是以装备制造商为核心企业，包含零件供应商、部件供应商、销售商和最终顾客，如图1所示。其中，零件供应商应承担零件的质量管理并提供给部件供应商，部件供应商应承担部件的质量管理并提供给制造商，制造商应承担产品的整体质量管理并通过销售商卖给最终顾客。因而，产品质量仅与零件供应商、部件供应商和制造商的质量管理行为有关。基于此，为进行装备制造业质量管理研究，本文构建由一个制造商、一个部件供应商和一个零件供应商组成的三级装备制造业供应链系统。

图1 装备制造业供应链

2.2 研究假设

(1)假设供应链上三方均为追求各自收益最大化的理性决策者，且t时刻制造商在质量管理上的努力程度为Am(t)，部件供应商在质量管理上的努力程度为As1(t)，零件供应商在质量管理上的努力程度为As2(t)，其中t(t∈[0,+∞))为时间变量。

(2)装备制造业的产品质量取决于零件供应商、部件供应商和制造商在质量管理上的努力程度，且均严格下凸。借鉴洪江涛[16]和夏兆敏[18]的研究假设，可用如下微分方程表示产品质量随时间的变化规律：

(1)

其中λm、λs1和λs2分别代表制造商、部件供应商和零件供应商的质量管理行为对装备制造业产品质量的影响程度，即质量影响系数；δ代表由于设备老化、技术落后等原因造成的供应链质量的相对衰减率，即质量衰减系数；Q0代表供应链的初始质量水平。

(3)假设供应链上三方的质量管理成本是关于各自质量管理努力程度的二次函数，即：

Cm(t)=μm2A2m(t)；Cs1(t)=μs12A2s1(t)；

Cs2(t)=μs22A2s2(t)

其中μm、μs1和μs2分别代表制造商、部件供应商和零件供应商的质量管理成本系数；而努力成本的上凸特性反映了企业边际成本递增原则，即企业的质量管理行为越好，进一步提升所需要付出的成本越大。

(4)装备制造业产品质量的改善可提高供应链的总收益，参考张雄会等[31]关于“产品质量与供应链收益呈线性函数关系”的研究假设，可得：

π(t)=φ+ηQ(t)

(2)

其中η代表产品质量对供应链整体收益的影响程度，即质量收益系数；φ是常数。

(5)假设制造商、部件供应商、零件供应商三方的信息是完全的，且拥有相同的贴现率r(r>0)。三方按照事先商定的比例分配供应链的总收益，其中部件供应商获得α1(0<α1<1-α2)，零件供应商获得α2(0<α2<1-α1)，则制造商获得(1-α1-α2)。同时，制造商对部件供应商质量管理成本的分担比例为β1(t)，部件供应商对零件供应商质量管理成本的分担比例为β2(t)，其中β1(t)，β2(t)∈[0,1]。假设上述模型中的所有参数均为与时间无关的正常数。(下文将省略时间t)

3 分散式决策

3.1 Nash非合作博弈

假设制造商、部件供应商和零件供应商地位平等，同时行动、独立决策以实现自身收益最大。此时，理性的决策者将不替其他企业分担质量管理成本，因而有β1=β2=0，则制造商、部件供应商、零件供应商的决策问题分别为：

结论1：Nash非合作博弈情形下，三级装备制造业供应链中制造商、部件供应商和零件供应商的最优质量管理行为分别是：

(3)

(4)

(5)

证明：假设制造商、部件供应商和零件供应商各自的最优收益函数为Vm(Q)、Vs1(Q)和Vs2(Q)，其应满足如下HJB方程，即：

(6)

(7)

(8)

使式(6)、(7)、(8)最大化成立的必要条件是一阶偏导为零，整理可得：

(9)

(10)

(11)

将式(9)、(10)、(11)分别代入HJB方程的右端部分，可得：

(12)

(13)

(14)

根据方程的特点可知，线性最优收益函数Vm(Q)=f1Q+f2、Vs1(Q)=g1Q+g2和Vs2(Q)=h1Q+h2满足式(12)、(13)、(14)，其中f1、f2、g1、g2、h1、h2为常数。将Vm(Q)、Vs1(Q)、Vs2(Q)和它们的导数代入式(12)、(13)、(14)，整理可得：

r(f1Q+f2)=[(1-α1-α2)η-δf1]Q+

(15)

(16)

(17)

分别对比式(15)、(16)、(17)左右两边Q的系数项和常数项，可求得参数值为：

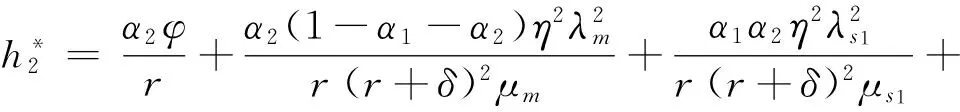
结论2：Nash非合作博弈情形下，制造商、部件供应商、零件供应商和三级装备制造业供应链的最优收益分别是：

(18)

(19)

(20)

(21)

证明：将式(3)、(4)、(5)代入式(1)，得：

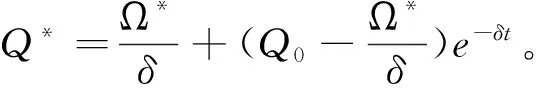
3.2 Stackelberg主从博弈

假设制造商是供应链的领导者，部件供应商和零件供应商是跟随者，供应链成员均以各自收益最大化为目标独立决策，决策时依照主从关系进行。首先制造商确定自身的最优质量管理行为Am及对部件供应商质量管理成本的分担比例β1；接着部件供应商在观察到制造商的决策结果后，选择自身的最优质量管理行为As1及对零件供应商质量管理成本的分担比例β2；最后零件供应商根据部件供应商的决策再决定自身的最优质量管理行为As2。

则制造商、部件供应商、零件供应商的决策问题分别为：

结论3：Stackelberg主从博弈情形下，三级装备制造业供应链中制造商、部件供应商和零件供应商的最优质量管理行为分别是：

(22)

(23)

(24)

(25)

(26)

证明：假设制造商、部件供应商和零件供应商各自的最优收益函数为Vm(Q)、Vs1(Q)和Vs2(Q)，均应满足HJB方程。采用逆向归纳法，首先分析零件供应商的最优收益问题：

使式(27)最大化成立的必要条件为As2的一阶偏导为零，可得：

(28)

进而分析部件供应商的最优收益问题：

(29)

理性的部件供应商应根据零件供应商的反应函数来确定自己的最优策略，即将式(28)代入式(29)，进而由最大化成立的一阶偏导条件，得：

(30)

(31)

最后分析制造商的最优收益问题：

(32)

理性的制造商应根据零件供应商的反应函数来确定自己的最优策略，即将式(30)代入式(32)，进而由最大化成立的一阶偏导条件，可得：

(33)

(34)

将式(28)、(30)、(31)、(33)、(34)分别代入HJB方程的右端部分，可得：

(35)

(36)

(37)

根据方程的特点可知，线性最优收益函数Vm(Q)=f1Q+f2、Vs1(Q)=g1Q+g2和Vs2(Q)=h1Q+h2满足式(35)、(36)、(37)，其中f1、f2、g1、g2、h1、h2为常数。将Vm(Q)、Vs1(Q)、Vs2(Q)和它们的导数代入式(35)、(36)、(37)，整理可得：

(38)

(39)

(40)

分别对比式(38)、(39)、(40)左右两边Q的系数项和常数项，可求得参数值为：

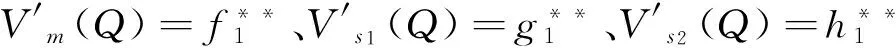
结论4：Stackelberg主从博弈情形下，制造商、部件供应商、零件供应商和三级装备制造业供应链的最优收益分别是：

(41)

(42)

(43)

(44)

证明：将式(28)、(30)、(33)代入式(1)，可得：

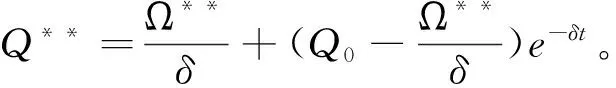
3.3 比较分析

推论1：分散式决策下，制造商的质量管理行为在两种博弈情形下相同；而与Nash非合作博弈相比，在Stackelberg主从博弈中，部件供应商与零件供应商的质量管理行为均得到改善，改善强度等于各自质量管理成本被分担的比例。

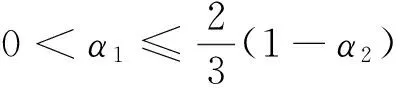
由推论1可知，制造商在供应链中处于核心地位，首先进行策略选择，因而其为部件供应商分担质量管理成本并不会影响自身在质量管理上的努力程度；而成本分担作为激励机制，可有效提高部件供应商和零件供应商在质量管理上的努力水平，充分调动双方质量管理的积极性。

推论2：分散式决策下，与Nash非合作博弈相比，在Stackelberg主从博弈中，制造商、部件供应商、零件供应商的最优收益及供应链整体收益状况均得到改善。

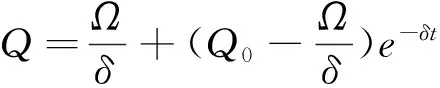
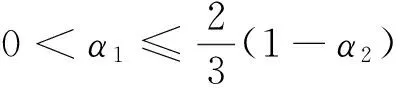
由推论2可知，成本分担可实现供应链成员及供应链整体的Pareto改进，形成共赢局面，因而与Nash非合作博弈相比，供应链成员更倾向于选择Stackelberg主从博弈。

4 集中式决策

4.1 协同合作博弈

假设制造商、部件供应商和零件供应商构成一个统一的利益主体，以供应链整体收益最大化为目标共同协商确定各自的最优质量管理行为，提高产品的整体质量。此时，成本分担仅属于供应链内部的资金转移，因而分担比例可在[0，1]上任意取值，不影响各参与方的策略选择。则供应链系统的决策问题为：

结论5：协同合作博弈情形下，三级装备制造业供应链中制造商、部件供应商和零件供应商的最优质量管理行为分别是：

(45)

(46)

(47)

证明：假设三级装备制造业供应链的最优收益函数为V(Q)，其应满足如下HJB方程，即：

(48)

使式(48)最大化成立的必要条件为Am、As1和As2的一阶偏导均为零，整理可得：

(49)

(50)

(51)

将式(49)、(50)、(51)分别代入HJB方程的右端部分，可得：

(60)

根据方程特点可知，线性最优收益函数V(Q)=k1Q+k2满足式(60)，其中k1、k2为未知常数。将V(Q)和它的导数代入式(60)，整理得：

(61)

分别对比式(61)左右两边Q的系数项和常数项，可求得参数值为：

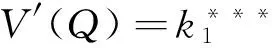
结论6：协同合作博弈情形下，三级装备制造业供应链的最优收益是：

(62)

证明：将式(45)、(46)、(47)代入式(1)，可得：

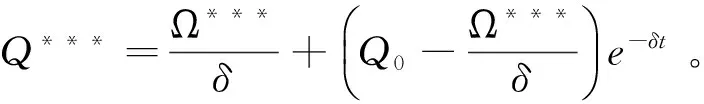
4.2 比较分析

推论3：集中式决策下制造商、部件供应商和零件供应商的质量管理行为均优于分散式决策。

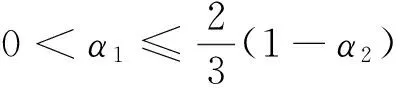
由推论3可知，集中式决策下，各参与方以整个供应链作为决策对象，因而可有效协调供应链成员间的质量管理行为，使得各参与方在质量管理上的努力程度达到最高，共同推进产品质量的提升。

推论4：集中式决策下三级装备制造业供应链的整体收益高于分散式决策。

由推论4可知，集中式决策下，供应链成员不再局限于自身收益的大小，而是以供应链整体收益最大化为目标进行决策，因而可实现供应链整体收益的增加，达到Pareto最优。

值得注意的是，虽然集中式决策下制造商、部件供应商和零件供应商的质量管理行为达到最优，供应链的整体收益达到最高，但各参与方还有自身的利益诉求。当各参与方在集中式决策下各自的最优收益低于分散式决策时，理性的决策者不会选择协同合作，即使一开始建立了合作关系，也不会长久。因而，为实现三级装备制造业供应链中制造商、部件供应商和零件供应商的质量管理行为协调，须满足如下参与约束条件：

方案一：延续之前的收益分配比例(α1、α2)，当某一方不满足参与约束条件时，通过其他成员的转移支付来解决。方案二：延续主从博弈中供应链成员的收益状况，并根据三方的讨价还价能力，通过协商确定协同合作超额收益(ΔV=V***(Q)-V**(Q))的分配比例。从而保证供应链成员的个体Pareto最优，进而实现装备制造业供应链质量管理行为协调。

推论5：Am与λm、η成正比，与μm、δ、r成反比；As1与λs1、η成正比，与μs1、δ、r成反比；As2与λs2、η成正比，与μs2、δ、r成反比。可由结论1、结论3和结论5分别求导得证。

由推论5可知，制造商、部件供应商和零件供应商的最优质量管理努力水平与质量影响系数、质量收益系数正相关，与质量管理成本系数、质量衰减系数、贴现率负相关。

综上所述，当制造商、部件供应商和零件供应商刚刚开始合作时，会选择“Nash非合作博弈的分散式决策”模式；随着合作的加深，各参与方会采取“Stackelberg主从博弈的分散式决策”模式以增加各自的收益；进而为适应现代市场竞争、实现合作关系深化，供应链各参与方将不再各自为政，而是加强战略合作，选择“协同合作博弈的集中式决策”模式以提高供应链整体收益水平。

5 算例分析

为了直观地表述制造商、部件供应商和零件供应商在不同博弈情形下最优质量管理行为和收益水平的比较分析结果，可利用算例对上述微分模型进行说明。假设模型中的参数设置如下：μm=0.5，μs1=0.4，μs2=0.2，λm=0.4，λs1=0.3，λs2=0.1，δ=0.1，φ=0.5，η=0.4，r=0.1，Q(0)=Q0=3，其中取α1=0.24和α2=0.16可同时满足限制条件0<α1≤(2/3)(1-α2)和α2/2≤α1<1-α2。则通过计算可得三种博弈情形下三级装备制造业供应链中制造商、部件供应商和零件供应商的均衡结果如表1所示。

表1 三种博弈情形下均衡结果的比较分析

图2 分散式决策下不同主体最优收益的比较分析

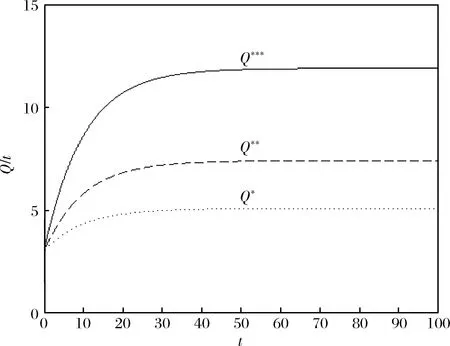
图3 三种情形下供应链产品质量的比较分析

图4 三种情形下供应链整体收益的比较分析

由图2和图4可知，分散式决策下制造商、部件供应商和零件供应商各自的最优收益，以及三种博弈情形下装备制造业供应链的整体收益水平均具有时间稳定趋向，随时间递增，前期波动剧烈，后期逐渐趋于平缓，最终收敛于均衡状态，说明供应链系统的动态变化得到了有效调控。且Stackelberg主从博弈情形下，制造商、部件供应商和零件供应商各自的最优收益水平及供应链整体收益水平始终高于Nash非合作博弈情形；而集中式决策下，供应链的整体收益达到最高，优于分散式决策。与推论2和推论4的结论相符。由图3可知，供应链产品质量的最优轨迹虽然随时间递增，但递增的速度越来越慢，表明随着供应链成员质量管理工作的不断投入，质量改善效果呈现边际递减趋势。

对于不满足限制条件的参数设定，一方面缺乏合适的图形界面，另一方面不是本文的研究重点，因而没有给出相应的算例分析。

6 结语

为提高装备制造业的产品质量，本文探讨了由制造商、部件供应商和零件供应商为节点成员的三级装备制造业供应链质量管理行为的协调问题。本文构建基于连续时间的微分对策模型，依次考察了Nash非合作博弈、Stackelberg主从博弈(分散式决策)和协同合作博弈(集中式决策)三种情形下供应链成员的最优质量管理行为、最优收益及系统整体收益状况，通过比较分析和数值模拟可以得到以下结论：(1)当供应链成员由Nash非合作博弈过渡到Stackelberg主从博弈时，制造商的质量管理行为保持不变，部件供应商和零件供应商的质量管理行为将得到改善，改善强度等于各自质量管理成本被分担的比例，而当供应链成员进行协同合作博弈时，各参与方的质量管理行为达到最优；(2)Stackelberg主从博弈情形下，制造商、部件供应商和零件供应商的最优收益均高于Nash非合作博弈，实现了Pareto改进，而对供应链系统整体收益而言，协同合作博弈结构最优，但前提是必须同时满足供应链成员的参与约束条件；(3)无论供应链成员选择何种博弈结构，其质量影响系数λ越高、质量收益系数η越大，则各参与方在质量管理上的努力程度越高；相反其质量管理成本系数μ越高、质量衰减系数δ越大、贴现率r越大，则各参与方在质量管理上的努力程度越低。

本文运用微分对策模型所得研究结论对于装备制造业供应链中企业的质量管理行为具有重要的现实指导意义。(1)分散式决策下，制造商通过分担部件供应商的质量管理成本以改善其质量管理行为，同理部件供应商通过分担零件供应商的质量管理成本以改善其质量管理行为，改善强度正好为各自质量管理成本被分担的比例，因而，成本分担比例越高，部件供应商和零件供应商质量管理行为的改善强度越大，产品质量越优；(2)分散式决策下，供应链成员均从各自收益最大化角度出发进行决策，成本分担使得制造商、部件供应商和零件供应商所获得的收益增加，实现了供应链成员收益及供应链整体收益的帕累托改进，因而成本分担是符合企业发展现状的供应链合作机制；(3)集中式决策下，供应链成员间将形成更紧密的合作关系，各个环节衔接的更好，使得制造商、部件供应商和零件供应商的质量管理行为达到最优、产品质量达到最高，因而协同合作可有效改善供应链成员的质量管理行为，提升产品质量；(4)集中式决策下，供应链成员均从整体收益最大化角度出发进行决策，实现了供应链整体收益的增加，但需要注意的是，必须采取科学合理的收益分配方案，以保证所有供应链成员的收益均得到提高，否则理性的决策者将选择通过成本分担实现自身收益最大化，因而满足供应链成员参与约束的协同合作才是供应链发展的最优模式；(5)质量影响系数、质量收益系数、质量管理成本系数和质量衰减系数是影响供应链成员质量管理行为的关键因素，因而企业可通过扩大质量影响程度、增加质量边际收益、降低质量管理成本、减缓质量衰减比率等措施来改善其质量管理行为。

当部件供应商和零件供应商为一个供应商时，即λs2=0且α2=0，通过数理计算可以发现，计算结果与洪江涛[16]和夏兆敏[18]的一致，说明二级供应链质量管理问题的研究是本文研究内容的一种特定情形，而本文构建的模型与研究结论更具有普适性，也更符合装备制造业的现实情况，是对普通二级供应链研究的进一步深化和扩展。

本文的不足之处在于：(1)为了便于计算与推导，对模型和参数进行了简化，因而后续研究可针对动态参数条件求解微分对策模型，也可考虑随机干扰因素对模型结果的影响，还可探讨产品质量服从一定概率分布时的均衡策略。(2)本文仅研究了一个制造商、一个部件供应商和一个零件供应商的质量管理行为协调问题，而复杂供应链网络中上下游之间如何进行质量管理也是值得研究的方向。(3)本文在构建模型时，只考虑了产品质量对供应链收益的影响，并未考虑其他变量，因而未来可进一步考虑引入产量、价格、广告等因素的作用。(4)在实践调研的基础上，如何将理论模型得到的一般结论应用于解决具体的供应链质量管理问题，也有待今后的深入探讨。

[1] Xu Lida. Information architecture for supply chain quality management [J].International Journal of Production Research, 2011, 49(1): 183-198.

[2] Kaynak H, Hartley J L. A replication and extension of quality management into the supply chain[J]. Journal of Operations Management, 2008, 26(4): 468-489.

[3] Kuei C, Madu C N, Lin C. Developing global supply chain quality management systems[J]. International Journal of Production Research, 2011, 49(15): 4457-4481.

[4] Cachon G P, Lariviere M A. Supply chain coordination with revenue-sharing contracts: Strengths and limitations[J]. Management Science, 2005, 51(1): 30-44.

[5] Handley S M, Gray J V. Inter-organizational quality management: The use of contractual incentives and monitoring mechanisms with outsourced manufacturing[J]. Production and Operations Management, 2013, 22(6): 1540-1556.

[6] Chao G H, Iravani S M R, Savaskan R C. Quality improvement incentives and product recall cost sharing contracts[J]. Management Science, 2009, 55(7): 1122-1138.

[7] Hsieh C C, Liu Y T. Quality investment and inspection policy in a supplier-manufacturer supply chain[J]. European Journal of Operational Research, 2010, 202(3): 717-729.

[8] Xie Gang, Yue Wuyi, Wang Shouyang, et al. Quality investment and price decision in a risk-averse supply chain[J]. European Journal of Operational Research, 2011, 214(2): 403-410.

[9] Xie Gang, Yue Wuyi, Wang Shouyang. Quality improvement policies in a supply chain with Stackelberg games[J]. Journal of Applied Mathematics, 2014, (3): 1-9.

[10] Shi Hongyan, Liu Yunchuan, Petruzzi N C. Consumer heterogeneity, product quality, and distribution channels[J]. Management Science, 2013, 59(5): 1162-1176.

[11] El Ouardighi F, Kogan K. Dynamic conformance and design quality in a supply chain: An assessment of contracts’ coordinating power[J]. Annals of Operations Research, 2013, 211(1): 137-166.

[12] Liu Weihua, Wang Yijia. Quality control game model in logistics service supply chain based on different combinations of risk attitude[J]. International Journal of Production Economics, 2015, 161: 181-191.

[13] Giri B C, Chakraborty A, Maiti T. Quality and pricing decisions in a two-echelon supply chain under multi-manufacturer competition[J]. The International Journal of Advanced ManufacturingTechnology, 2015, 78(9): 1927-1941.

[14] Liu Guowei, Sethi S P, Zhang Jianxiong. Myopic vs. far-sighted behaviours in a revenue-sharing supply chain with reference quality effects[J]. International Journal of Production Research, 2016, 54(5): 1-24.

[15] 周明，张异，李勇，等．供应链质量管理中的最优合同设计[J]．管理工程学报，2006，20(3)：120-122．

[16] 但斌，任连春，张旭梅．质量影响需求下的二级供应链协调模型研究[J]．工业工程与管理，2010，15(4)：1-4．

[17] 蒲国利，苏秦，刘强．一个新的学科方向——供应链质量管理研究综述[J]．科学学与科学技术管理，2011，32(10)：70-79．

[18] 胡军，张镓，芮明杰．线性需求条件下考虑质量控制的供应链协调契约模型[J]．系统工程理论与实践，2013，33(3)：601-609．

[19] 夏兆敏，孙世民．基于微分博弈的二级猪肉供应链质量行为协调机制研究[J]．运筹与管理，2014，23(2)：198-205．

[20] 于荣，唐润，孟秀丽，等．基于行为博弈的食品安全质量链主体合作机制研究[J]．预测，2014，33(6)：76-80．

[21] 朱立龙，于涛，夏同水．两级供应链产品质量控制契约模型分析[J]．中国管理科学，2013，21(1)：71-79．

[22] 朱立龙，夏同水，许可．非对称信息条件下两级供应链产品质量控制策略研究[J]．中国人口资源与环境，2014，24(5)：170-176．

[23] 申强，侯云先，杨为民．双边道德风险下供应链质量协调契约研究[J]．中国管理科学，2014，22(3)：90-95．

[24] 石丹，李勇建．基于契约和关系治理的供应链质量控制机制设计[J]．运筹与管理，2014，23(2)：15-23．

[25] 刘威延，苏秦．不完全信息均衡向完全信息转化的供应链质量合同设计[J]．系统管理学报，2015，24(5)：748-755．

[26] 古川，罗峦．消费者质量识别对农产品供应链质量和价格决策的影响[J]．管理评论，2016，28(12)：225-234．