基于韧性城市视角的冰雪天气下路网恢复问题研究

王 晶,刘昊天,朱建明

(1．北京工商大学商学院，北京 100048；2.中国科学院大学工程科学学院，北京 100049)

1 引言

随着城市化的快速发展，当今城市越来越依赖于水、电、燃气、交通、通讯、等城市重要基础设施提供的服务。因此，关键基础设施保护和恢复是应急管理的重要内容[1]。当城市受到外界冲击后，如果关键基础设施不能快速恢复，极易造成严重损失。在城市保障运行的各子系统中，交通系统是极其重要的。相比于降雨天气，在冰雪天气下城市道路基础设施面临更严峻挑战，极易造成整个路网交通的混乱乃至中断。然而，全球气候变暖逐年加剧，导致冬季极端冰雪天气事件频发，给城市交通路网带来严重威胁。2011年1月26日，一场雨夹雪袭击了美国东北部三州，纽约市区道路积雪厚度一度达到20厘米，市区公交全部暂停运营，华盛顿地区在降雪三小时后交通就陷入瘫痪，连总统车队也被困于拥堵之中，降雪结束12小时后，市区交通才逐渐恢复正常。2015年11月22日，京津冀普降大雪，北京市启动道路结冰黄色预警，路网交通运行面临严峻挑战。为应对突如其来的冰雪天气，防止路面积雪结冰，北京市共出动专业作业人员3.7万人，发动扫雪铲冰群众4.7万人，施撒融雪剂13824吨，缓解了次日早高峰的交通拥堵。由此可见，极端冰雪天气已经成为影响全球大中型城市交通运行的重大威胁，而准确高效的应急准备工作尤为关键。因此，研究如何降低冰雪天气对城市路网系统的冲击并使路网快速恢复对于城市交通系统平稳运行具有重要意义。

路面融雪除冰工作是应对冬季冰雪天气的关键。对于冬季路网除雪问题，有众多学者进行了研究。在优化目标方面，一些学者以作业车辆空驶、行驶距离最短或除雪作业成本最小作为优化目标。例如，Fu Liping等[2]以车辆空驶距离最短为优化目标，研究了基于实时信息的冬季路网维护作业优化问题。Dussault[3]等研究了冬季机械除雪作业问题，并提出使除雪车的上坡作业路段里程最小化的优化目标，以降低融雪除冰成本。Muyldermans等[4-5]以除雪成本最小化为目标，研究了融雪剂布撒作业的区域划分问题，以及基于弧路径优化的融雪剂布撒车辆路径规划方法。Perrier等[6]以除雪作业经济成本最低为目标，提出了冬季除雪作业分区设计方法及其求解算法。这些文献更多地是从成本角度优化路网除雪问题。而在极端冰雪天气条件下，应急管理的弱经济性凸显，因此一些学者便从除雪作业时间的角度对策略进行优化。例如，Quirion-Blais等[7]提出在紧急情况下，应以各优先级路段的加权作业时间最短为目标求解大规模除雪车辆路径优化问题。谢秉磊等[8]对融雪剂布撒优化问题进行了研究，提出了带临时补充点的融雪剂撒布车辆路径优化问题，增强了车辆作业的持续性，缩短除雪作业总时间。然而，无论是经济成本还是作业时间，这些优化目标仅能够从单一方面反映除雪作业的需求，缺乏除雪作业对路网交通恢复的整体性和系统性考量。

随着城市化进程加快，如何降低城市自身脆弱性并提升城市系统面对突发事件的恢复能力，日益受到了学界和政府的高度关注，“韧性城市”这一概念应运而生。自1973年Holling[9]将韧性概念引申到生态学后，韧性概念在众多领域内不断发展。当韧性与城市学结合后，开始出现“韧性城市”的概念。目前，新加坡、日本等已经将打造韧性城市列为国家战略，国内的通州，海盐等城市均已提出建设韧性城市的目标。韧性一词目前尚无统一定义，但可解释为城市系统能够消化吸收外界干扰，保持原有结构、功能和主要特征的能力。此概念将城市视为一个复杂系统，重点强调系统整体在受冲击后的承载能力和恢复能力两方面[10]。

生命线基础设施是城市的命脉，韧性城市的建立与其基础设施的韧性息息相关。关于基础设施的韧性评价方法，有众多学者对其进行研究。城市路网韧性与配电网韧性有较高的相似性，高海翔等[11]对配电网的韧性及相关研究进行了梳理，利用配电网在灾难后的动态响应曲线，从鲁棒性和迅速性两方面定义用于配电网调度运行的韧性指标。这两方面代表了配电网的对突发灾害的承载能力和灾后恢复能力。Aven[12]对风险、脆弱性和韧性的概念、定义和分析框架进行了评述，分析了这三者之间的联系和区别，并初步提出了韧性的度量方法。Cen和Sansavini[13]将基础设施的韧性分解为三个指标：吸收能力、适应能力和恢复能力，并以瑞士配电网模型为例分析了韧性的度量方法并提出了增强配电网韧性的策略建议。关于路网韧性。Tran[14]等提出了一种衡量系统韧性的度量方法，该方法主要集中在系统对外界扰动的吸收性、恢复性和适应性上，并对信息交换网络进行建模仿真，结果表明提高系统韧性可以增强系统对随机或目标性威胁的应对能力。

然而，以往文献在研究冬季路网除雪作业优化问题时，多以作业车辆空驶、行驶里程最短[2-3]、除雪作业成本最低[4-6]除雪作业时长最短[7-8]作为优化目标，难以系统性地评价除雪作业对路网的动态恢复过程。另外目前的冰雪天气下路网恢复应对策略中仅考虑了除雪作业车辆的路径优化，较少考虑到对除雪物资的提前布局，而应急物资的有效布局不仅实际上是城市突发事件响应的前提，是突发事件快速响应的有效保障。应对冰雪天气的城市路网恢复问题应将除雪应急物资布局与冰雪天气后作业车辆路径规划进行集成优化研究。

为此，本文在研究中提出几点新思路。在优化目标方面，本文提出以韧性增强作为城市路网恢复的优化目标，利用韧性所包含多个指标来动态地、系统地衡量城市路网的突发事件承受能力与恢复过程，全面提升城市路网对抗极端冰雪天气的能力；在韧性恢复措施的创新方面，本文将冰雪天气前的除雪应急物资布局与冰雪天气后车辆作业路径安排进行集成优化研究，保证决策方案的全面性，同时将机械式铲雪和融雪剂融雪两种融雪除冰方法有机结合，提高除雪作业的有效性；另外，利用独立路径而非传统路径的通行速度评价城市路网服务能力，提高了模型求解的效率。本文将从韧性的角度出发，优化除雪应急物资布局，并在既定布局方案下规划除雪车辆作业路径，有利于提高城市路网路网冰雪天气下的抗冲击能力和恢复能力，提高城市整体韧性，为城市交通与应急管理部门制定有关决策提供参考。

2 冰雪天气下的城市路网韧性概念与度量方法

本节对城市路网韧性的概念进行分析和阐述，结合以往研究成果，建立冰雪天气下城市路网韧性的评价指标，分析得出其度量方法，为优化冰雪天气下的城市路网恢复策略优化奠定基础。

2.1 城市路网服务能力评价方法

本文主要研究冰雪天气下的城市路网系统的恢复问题。这里的恢复主要是指路网服务能力的恢复。考虑到城市路网的服务主要是帮助交通参与者快速有效地从路网中某个节点到达另一节点[15]，我们提出一种假设，即采用平均车速衡量路网服务能力。

由于城市路网是一个复杂的网络系统，抽象出的网络图中包含了大量的起点-终点点对(Origin- Destination pair),简称OD点对。每个OD点对之间可能包含了大量可行路径。如果对每条可行路径的平均车速都进行考察，将消耗较长的计算时间，难以满足应急管理的要求。而独立路径(Independent Pathway，IPW)相比于一般路径，由于其具有数量较少，易寻找，重复信息较少等特点，更适合作为评价城市道路系统的研究对象[16]。因此，本文只考察路网中全部OD点对间所有独立路径上的平均车速，以此评价路网系统功能水平。

城市路网由交叉口(节点)和路段(弧)共同构成，可以将其抽象成加权无向网络图，权重代表道路长度，假设所有路段均为双向车道，某简单路网可如图1所示。

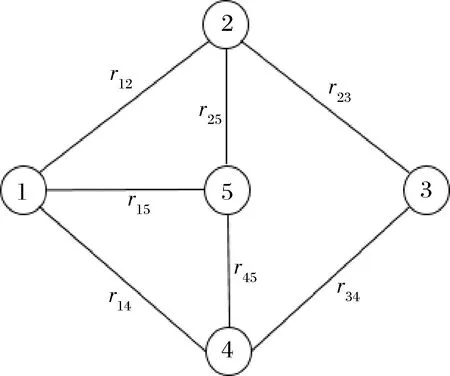
图1 路网拓扑结构示意图

城市路网系统中，两节点间的路径由多个路段连接而成。独立路径是指两点之间互不与其他路径共享路段的一类路径集合[15]。一个OD点对间的所有独立路径组成了属于该OD点对的独立路径集合。例如，图1中，点2至点4的某个可能的独立路径集合内共有三条独立路径，分别是2-1-4、2-5-4和2-3-4。在此集合内，2-5-1-4只是点2和点4之间的一条普通路径而非独立路径，因为其与独立路径2-1-4共同包括了路段r14。当然，路径2-5-1-4也可以与其他路径共同构成一个满足要求的独立路径集合。

一个OD点对间的最大独立路径数量被公式1约束。

N(i,j)=min{di,dj,nc(i,j)}

(1)

其中，N(i,j)为点i和点j间独立路径数量的上限。di,dj分别为点i和点j的度，nc(i,j)为点i和点j间的割的最少边数。nc(i,j)满足公式(2)。

N(i,j)=min{|Ck||Ck∈Ci,j}

(2)

其中Ci,j为点i和点j间的割集。

实际上城市路网的拓补结构通常是非完全图，为简化计算可以将OD点对间的独立路径数量上限等同于等于两点的度的最小值。利用Ip和Wang Dingwei[17]提出的独立路径搜索算法可以较快速地寻找路网中独立路径。在度量城市路网韧性之前，需要从路网中获取所有OD对间的独立路径，再对每个OD点对的独立路径进行分析。这样可以大大减少决策制定的运算量，同时不影响分析过程的准确性。

基于上述分析，本文将城市道路基础设施服务能力定义为所有独立联通路径上的平均车速。平均速度反映了某一路段对于交通参与者的服务能力。平均车速越高，则交通参与者能够越快地从出发点抵达目的地。而冰雪天气造成的路面积雪会严重影响车辆行驶。驾驶者为保证车辆安全，会根据积雪厚度情况适当降低行车速度。因此路段平均车速会随积雪厚度增加而降低，即路段服务能力随积雪厚度增加而降低。

《美国道路通行能力手册2010》指出: 小雪和大雪天气下车辆行驶速度分别下降8%～10%和30%～ 40%[18]。由此可见，路面积雪厚度是影响车辆平均速度的主要原因之一。为便于计算，假设路段平均车速与路段积雪厚度呈简单线性关系且积雪越厚路段平均车速越慢，根据《美国道路通行能力手册2010》的相关数据进行拟合车辆平均速度与积雪厚度的关系，可得公式(3)表示：

(3)

其中，vij为路段rij的平均车速，hij为路段rij的积雪厚度。

路段平均车速与路段积雪厚度的关系可用图像表示。如图2所示。当路段积雪深度大于20cm时，将导致路段交通瘫痪，此时路段平均车速为0Km/h。

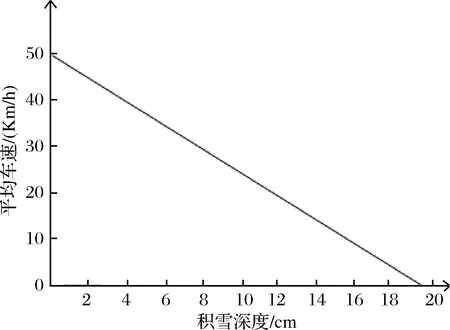
图2 不同积雪厚度下行驶车辆的平均车速

由独立路径中的各路段平均车速vij和路段长度lij可以求得该独立路径的整体平均车速用公式(4)表示：

(4)

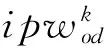
把全部独立路径考虑在内，我们认为路网系统中的总平均车速越高，则该路网的服务能力值MOP(Metric of Performance)越强。

(5)

其中，N为路网中点对数量。

2.2 冰雪天气下城市路网韧性的概念

本文依据城市路网在冰雪天气下的系统服务能力动态响应数据，从吸收能力和恢复能力两方面来定义冰雪天气下的城市路网韧性[19]，将这两方面能力有机结合，多角度系统性地度量路网恢复过程的有效性。

典型的冰雪天气下城市路网的系统功能变化曲线如图3所示，其中包含了路网对外来冲击的吸收能力和恢复能力。

如图3所示，路网在正常状态下初始服务能力值为MOP0。本文假设冰雪天气在T0时刻开始对路网造成冲击，路网服务能力不断下降，同时道路融雪除冰作业开始进行。至Td时刻，路网服务能力降至最低值MOPmin，我们将T0至Td这段时间称为吸收期(absorbing period)。之后随着天气好转以及道路疏通作业的不断进行，路网服务能力开始恢复。至Tmax时刻，系统功能恢复为新的稳定值MOPnew，此时路网恢复过程结束。我们将Td至Tmax这段时间称为恢复期(Recovering Period)。冰雪天气下的路网波动过程由T0时刻开始至Tmax时刻结束。

路网对冰雪天气冲击的吸收能力表现在吸收期时长和系统服务能力初始值与最低值之差两个指标中。对此我们可以理解为：吸收期越长，则路网服务能力从正常状态(初始值)到崩溃(最低值)的时间越久，表现为路网服务能力的衰退是缓慢的，路网可以在较长时间内不断吸收来自冰雪天气的冲击，保持较高的服务能力。这反映了路网对冲击的吸收能力较强；路网服务能力初始值与最低值的差越小，说明路网系统在面外来冲击时的服务能力损失越小，说明路网的吸收能力较强；路网的恢复能力则由恢复期时长和最终系统功能值两个指标体现。恢复期越短，表明路网在受冲击后恢复迅速，恢复能力强；最终服务能力值越高，则说明路网系统在受冲击后能较好地恢复至系统正常水平，说明恢复能力较强。

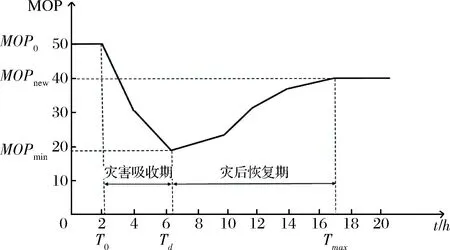
图3 某冰雪天气情景下的路网服务能力随时间变化情况

2.3 冰雪天气下城市路网韧性的度量方法

对于系统韧性的度量方法，众多学者通过研究给出了自己的观点，但目前尚无统一公式。其共性是从系统功能随时间的动态响应情况中提取关键指标，量化系统韧性。Francis和Bekera[19]在其研究中将度量路网系统韧性的公式简化为：

(6)

其中，ρi为系统韧性，Fd为系统能力恢复过程中的最差值，Fo为系统能力遭受冲击之前的初始状态值。

本文基于上文对城市路网韧性的概念的分析，在公式6中引入时间指标，将路网韧性(Res)用如下公式表示，公式符号参照图3。

(7)

其中，(Td-T0)为吸收期时长，(MOP0-MOPmin)为冰雪天气冲击下路网服务能力的最大损失值。在其他指标不变的情况下，吸收期时长与路网韧性呈正比关系，路网服务能力的最大损失值与路网韧性呈反比关系；(Tmax-T0)为路网波动过程总时长，其值为吸收期时长与恢复期时长之和，(MOPnew-MOPmin)为最终路网服务能力稳定值与最低值的差。当其他指标不变的情况下，路网恢复总时长与路网韧性呈反比关系，最终路网服务能力稳定值与最低值的差与路网韧性呈正比关系。由公式(7)可知，Res∈[0,1]，Res值越高表示路网韧性越强。

在实际决策时，往往需要在冰雪天气信息不确定的条件下，制定强鲁棒性的策略。本文利用离散情景集合表示冰雪天气的不确定性，集合中每个情景具有其特性与预期发生概率。采用情景识别技术对某地区历年冰雪天气事件的相似度进行分析，建立具有当地特点的冰雪天气情景库[20]。库内冰雪天气的特征参数包括降雪速度、降雪范围、持续时间、情景发生概率等。

在冰雪天气下的路网恢复问题中，城市路网韧性的内涵是指多种可能情景下的韧性期望值。如果考虑冰雪天气的不确定性，用S代表冰雪天气情景集合，则公式7应改进为：

(s∈S)

(8)

其中Ress为冰雪天气情景s下的路网韧性值。进而，路网韧性期望值可用公式表示如下：

(9)

其中ps为情景s的发生概率。

本章明确了城市路网服务能力的评价方法以及城市路网韧性的度量方法，确定了路网恢复作业决策的优化目标，为冰雪天气下城市路网恢复优化模型的建立奠定基础。

3 冰雪天气下的城市路网恢复优化模型

冰雪天气导致城市路网路面积雪结冰，路网内平均车速严重下降，导致路网服务能力急剧下降甚至完全瘫痪。为此，城市管理部门须根据该地区历史气象数据，建立符合当地特点的冰雪天气情景集合。在冰雪天气来临前完成对除雪应急物资的布局工作，并在此布局的基础上制定各情景下的融雪除冰工作预案。实现冰雪天气发生后路网恢复工作的快速启动，帮助城市路网抵抗外界冲击。

3.1 问题描述与模型假设

本文中的路网恢复问题决策包括以下两个方面：降雪前除雪应急物资布局方案和降雪后除雪作业车辆的路径规划。其中布局方案包括物资中心的选址和物资储存量决策；除雪作业路径规划包括机械除雪车和融雪剂布撒车的行驶路径和作业路段。

某路网恢复方案示意图如图4所示，该路网中共有三个备选物资中心可供选择，其中站点1和站点2为实际建立的物资中心。空心箭头表示除雪车辆的空驶路径，而蓝色箭头代表除雪车辆的作业路段(进行铲雪或融雪剂布撒)。

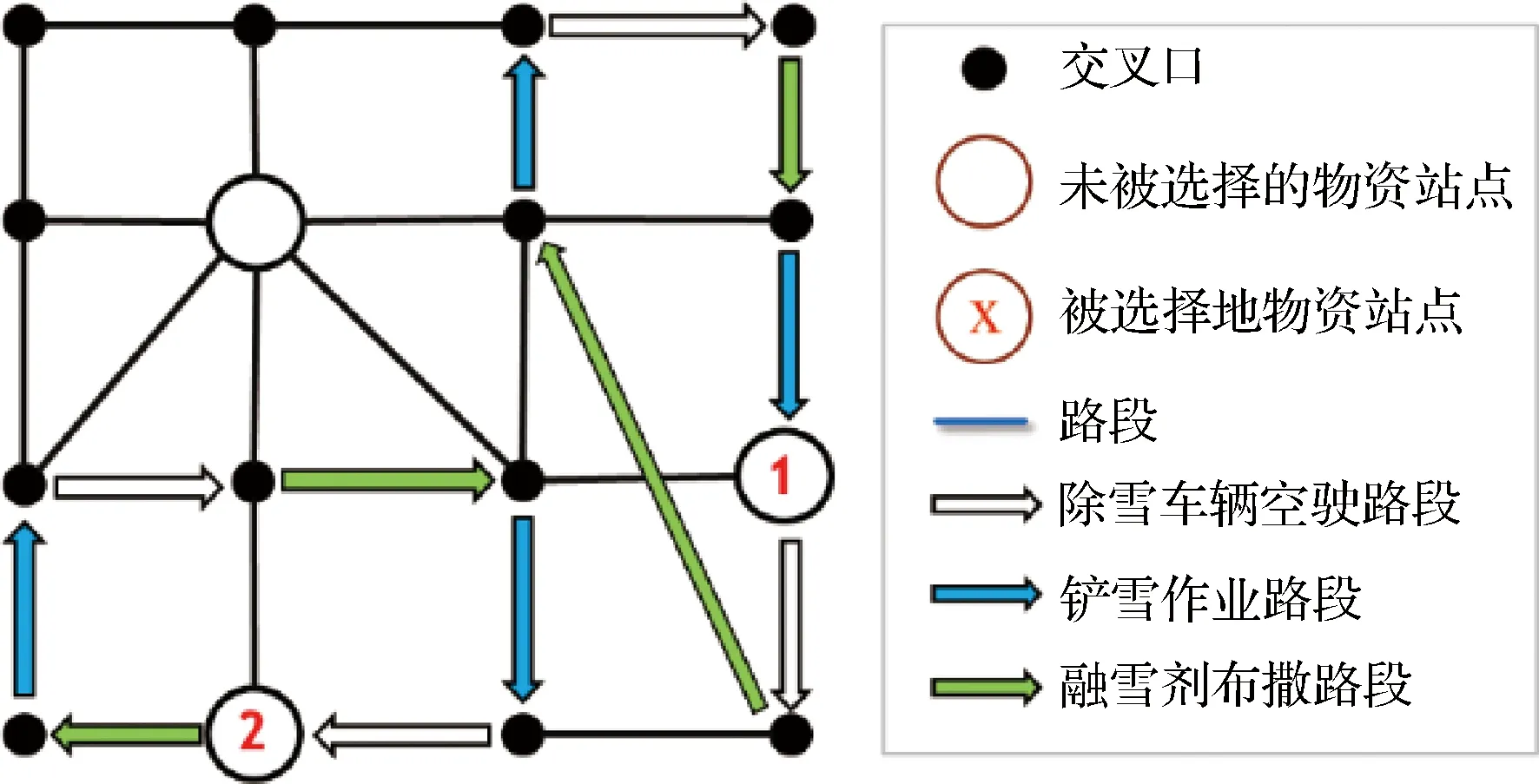
图4 路网恢复方案示意图

模型假设：

(1)除雪物资站没有容量上限，每个物资站内配备融雪剂布撒车和机械铲雪车各一台；

(2)除雪车辆配备有移动补给车保障资源供给，因此除雪车辆没有行驶里程上限，且作业过程中无需返回站点补给；

(3)作业车辆在空驶与作业两种状态下的行驶速度不同，空驶状态下的速度与当时道路平均车速相等，作业状态下的行驶速度为定值；

(4)路网在除雪作业完成后其服务能力一定能够达到新的稳定值。

集合与参数：

S：冰雪天气情景集合.

V：道路交叉口节点集合.

R：路段集合.

V*：备选应急物资中转中心集合.

IPWkj中转点k到交叉口j的独立路径中的路段集合，如果k点与j之间不存在独立联通路径，则IPWkj=∅。

IPWij:交叉口i到交叉口j的独立路径中的路段集合，如果i点与j之间不存在独立联通路径，则IPWij=∅。

rij：节点i和节点j之间的路段,rij∈R。

ps：冰雪天气情景s出现的概率。

li,j：路段rij的长度。

vij,s,t：情景s下t时刻路段rij的行车速度。

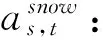
avehi：除雪车除雪速率(avehi=-M)。

amelt：融雪剂除雪速率。

tmelt：融雪剂的有效融雪时长。

aij,s,t：情景s下t时刻路段rij的积雪堆积速度。

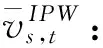
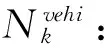
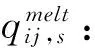
P：该年度冰雪天气道路保障总预算。

Pmelt：单位数量的融雪剂成本。

Pvehi：除雪车行驶的单位距离成本。

MOPs,t情景s下t时刻的路网服务能力。

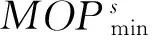
Ress：情景s下的路网韧性。

Res：天气情景集合下的路网期望总韧性。

决策变量：

xk：是否选择备选点k作为除雪物资站。

qk：除雪物资站的融雪剂储备量。

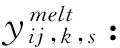
yij,k：情景s下rij是否在物资中转点k的覆盖范围之内。

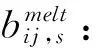
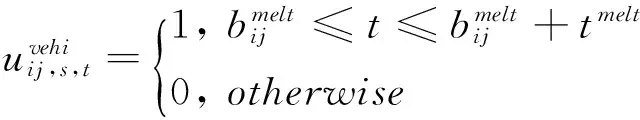
3.2 约束条件

(10)

qk≤xk*M

(11)

(12)

(13)

(14)

(15)

(16)

h,i∈V;j∈V∪V*,s∈S

(17)

h,i∈V;j∈V∪V*,s∈S

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

(26)

由目标函数式10可知，该路网恢复问题的数学模型优化目标为各情境下的路网期望韧性最大。在模型约束部分中，式11表示只能在被选中的备选物资点处储备除雪应急物资；式12和式13表示融雪剂布撒车和机械铲雪车只能对其行驶路径中的部分路段进行融雪除冰作业；式14表示每个路段只进行一次除雪作业；式15说明每个路段只能隶属于一个物资中转点;式16表示物资中心k的车辆只能在负责路段内实施作业；式17和式18为路段rij被融雪剂布撒车和机械铲雪车疏通的完成时间约束;式19和式20为路段rki被雪剂布撒车和机械铲雪车疏通的完成时间; 式21约束了预算总成本，总成本P为应急预案中的给定值;式22为路段rij的积雪堆积速度表达式，若aij,s,t为正表示路段积雪加深，若aij,s,t为负表示路段积雪融化；式23表示路段rij在情景s时刻t的积雪深度; 式24给出了除雪工作完成总时间；式25表示情景s下的路网服务能力最差值；式26表示除雪完成后的路网服务能力稳定值；

4 基于路段等级划分禁忌搜索的模型求解算法

城市路网恢复包括除雪物资布局优化和除雪车辆作业规划这两方面问题。在韧性视角下对城市路网应急除雪物资布局与除雪作业安排的集成优化属于典型的LRP(Resource Location and Vehicle Routing Problem)，可将其拆分为LAP (Location and Allocation Problem)和VRP两个子问题来求解[21]。LAP负责对除雪应急物资进行定位和分配；在LAP求解物资布局的基础上，求解VRP对每个物资中心内除雪车和融雪车的作业路径进行规划。两个子问题紧密联系，随迭代而同步优化。由于LAP和VRP均属NP-难问题，因此需要设计启发式算法进行求解。另外，还需要考虑到路段位置对路网韧性恢复的影响。由于路网中某些路段处在“枢纽”位置，其路况对路网服务能力的影响较一般路段更大，这类关键路段的物资需求应被优先满足。因此，路段等级划分就显得尤为重要。

4.1 路段等级划分方法

为了更好地应对可能发生的极端天气所带来的冲击，在极端天气潜在发生区域内考虑道路特征进行应急设施的选址是非常必要的[22]。本文在LAP和VRP的优化过程中引入路段等级作为参考，保证关键路段被优先分配资源。各路段的关键程度由该路段在路网中所有独立路径中的出现频次决定，以分级阈值α作为路段等级划分标准。出现频次高于阈值的路段为关键路段，出现频次低于阈值的路段为非关键路段，路段分级模型表示如下：

模型参数：

Lij：路段rij的等级数。

α：路段分级阈值。

nij：包含路段rij的IPW数量。

rij∈R

(27)

经过上式划分服务等级后，路段等级将作为分配除雪资源的重要参考指标，关键路段能优先获得融雪物资并予以优先除雪作业。关于路段关键度的服务等级划分，目前尚没有明确的划分标准，需要根据实际情况设定分级阈值。

4.2 LAP子问题与VRP子问题求解方法

冰雪天气发生前设立的应急物资储备中心是应对天气冲击的重要保障，其选址的合理与否直接关系到对突发情况的应急响应能力[23]。除雪物资布局的原则是每条待疏通路段只由一个应急除雪物资中心负责且各物资站的作业负担应尽量接近。因此应首先确定各个冰雪天气情景下每个物资中心的负责路段。进而由各路段对融雪剂的需求量并结合成本总预算进行物资中心的选址和资源量的分配。

依次将每个关键路段分配给距离其最近的物资站点，直到所有关键路段被分配完毕。在有作业负担的备选点处建立除雪物资站点，物资站点数量为k，k∈K。之后为每个物资站点分配非关键路段。依次为每个物质站点分配一条非关键路段，如此循环，直到所有非关键路段都被分配，构建情景s下物资站点k的服务路段集合Ck.s。某情景下的各物资站点融雪剂最佳储备量即为其所负责路段的融雪剂需求量之和。

(28)

由于存在多个冰雪天气情景且物资布局须在极端天气发生前完成，所以应根据每种情景下各站点的融雪剂储备量以及各情景发生概率，制定较为权衡的物资布局方案。设Qk为最终物资布局方案中物资站k的融雪剂储存量，则：

(29)

在完成除雪物资中心定位和服务路段分配之后，需要对除雪车辆的路径进行优化，即求解|K|个独立的VRP。为了便于算法中的搜索和迭代操作，需要对车辆的行车路径算子进行编码。

作业车辆由场站出发，对场站负责路段进行融雪除冰作业，完成后返回场站。路径算子的编码均可分为三部分：首位、中间部分和末位。其中首位和末尾的编码分别表示作业车辆出发的场站和结束后返回的场站。本文中所有算子的首位码和末位码相同。对于中间部分的编码，在每次产生新的搜索算子时都要保证关键路段出现在非关键路段之前，保证关键路段被优先疏通。例如某算子编码为。

4-8-5-7-9-4

表示该车辆从4号场站出发，最后返回4号场站。中间首先优先对关键路段r48和r85进行疏通，空驶路段r79后，对非关键路段r79进行疏通，再空驶路段r94返回4号场站。

4.3 改进的禁忌搜索模型求解算法

在除雪物资布局分配以及待服务路段子集划分完成之后，实际上模型被分解成了多个子模型，每个子模型都可看作为独立的除雪车辆路径优化问题。禁忌搜素的思想最早由Glover提出，是一种全局逐步寻优的启发式算法。该算法通过引入一个灵活的存储结构和相应的禁忌准则来避免迂回搜索，并通过藐视准则来赦免一些被禁忌的优良状态，进而保证多样化的有效探索以最终实现全局优化。本文的模型求解算法步骤如下。

步骤1：生成新的物资中心位置选择方案并为各中心分配作业路段

步骤2：在步骤1中的定位-分配方案下生产车辆作业路径的初始解并将其指定为当前解。

步骤3：对当前解进行扰动随机生成一组邻域解。扰动包括交叉、对调、删除等操作，并且从邻域解中剔除不可行解。

步骤4：从邻域解中选择并指定其作为当前解，重置禁忌表为空。根据目标函数值评估当前候选解。如果当前候选解的目标函数值优于当前最优值，前往步骤5；否则前往步骤8。

步骤5：查找当前候选解是否包含在禁忌表

中。如果是则前往步骤6；否则转

步骤7。如果某个候选解在步骤3

中的n次迭代内曾为最优解，则其

储存在禁忌表中。

步骤6：进行特赦准则检查。如果通过则前

往步骤7；否则转至步骤8。禁忌

表中的解如果通过了特赦准则，则

转化为当前最优解。

步骤7：将该候选解设置为当前可行解，更新禁忌表中的当前最优值。

步骤8：检查是否遍历所有邻域解。如果是则前往步骤9，否则返回步骤4；

步骤9：指定当前解(包括资源定位-分配方案)为最优可行候选解。更新禁忌表。

步骤10：检查是否达到算法停止准则。若则结束算法，输出结果；否则转至步骤1。

5 算例仿真

5.1 模型构建

以我国北方某城市路网为研究对象构建算例，将其城区内局部交通网络抽象为加权无向图，如图5所示。该路网中共有21个交叉口，29个路段，节点4、9、12、15、17 为备选物资中心，假设每个选取的物资中心拥有1辆除雪车辆。各路段长度如表1所示。通过独立路径搜索算法可以找出该路网中所有OD对间的独立路径。

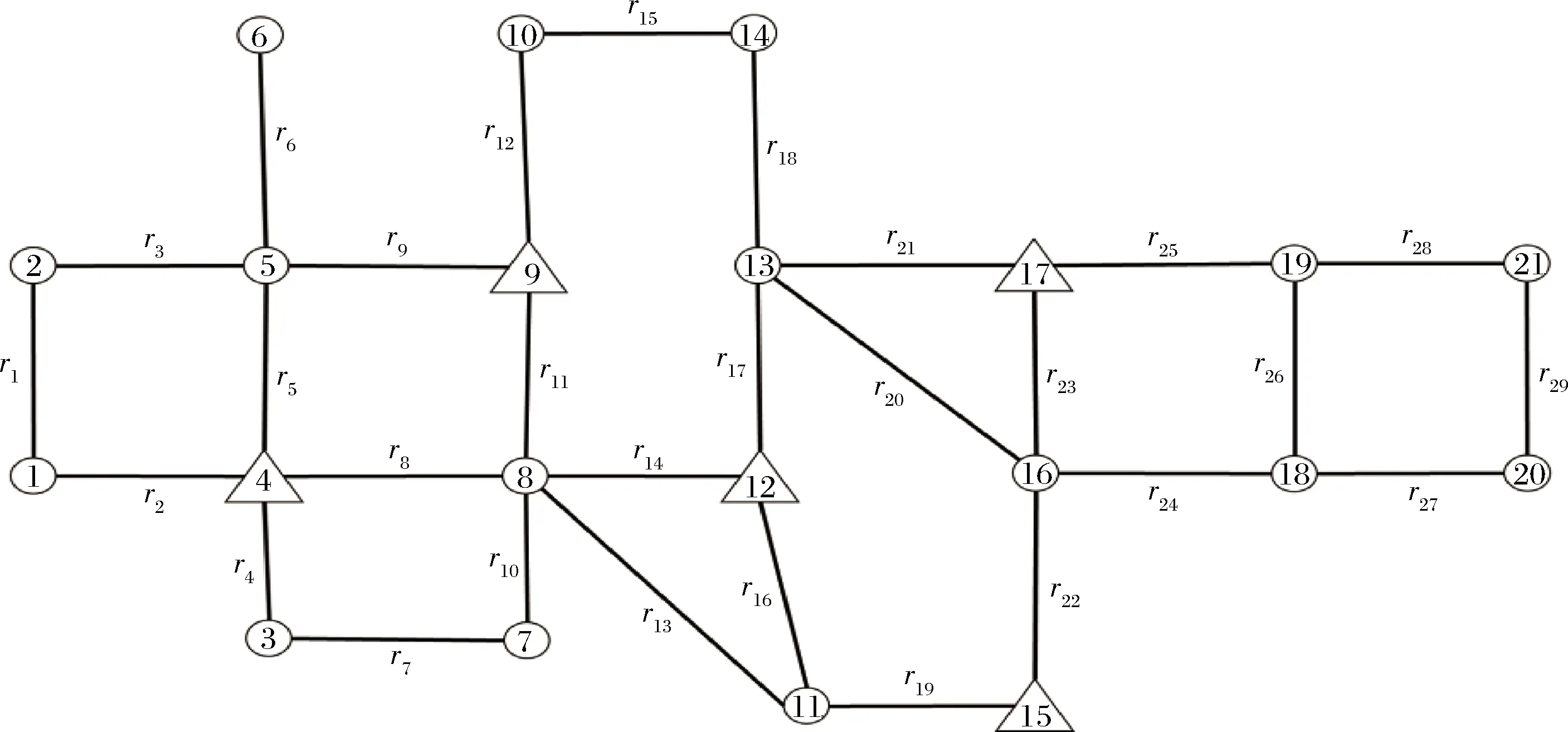
图5 路网拓补结构示意图

路段编号路段长度/Km路段编号路段长度/Km路段编号路段长度/Km1411421625127227331310235421442445415525566167263741742758518728396194294103209\

面向城市灾害情景，应急决策者需结合历史案例构建合理的知识系统以提升灾害应对能力[24]。本文根据该城市的冬季历史天气信息，建立起包含十种天气情景的冰雪天气情景库，这些离散情急基本能够代表该城市所有可能发生的冰雪天气。在情景库中，假设存在两种降雪速度，分别为5cm/h和10cm/h。每种天气情景的特征还包括影响路段和降雪持续时间以及其发生概率。某次天气预报显示未来几天内可能出现情景库内的三种冰雪天气，其预报信息如表2所示。

此外，除雪作业过程中的参数包括：除雪车和融雪剂布撒车在路网中的除雪速度取10km/h，空驶速度等于所在路段的平均行驶速度；单位融雪剂的融雪速率取1cm/h,有效融雪时长取3小时；除雪车除雪速度取-M，表示机械除雪车能够完全清除路段上的积雪；单位长度道路的融雪剂需求量最大值为1吨/公里，融雪剂价格为100元/吨；除雪车作业成本为200元/公里。除雪应急物资中心的固定费用为2000元/处，该冰雪天气下年度道路保障总预算为130万元。

表2 三种可能的冰雪天气情景信息

在模型中设定以上参数，经模型求解算法计算，获得融雪物资布局方案(三种物资数量均为0表示该物资中心未被选取)，如表3所示：

表3 融雪物资布局优化方案

表4 不同冰雪天气情景下的除雪作业路径优化方案

5.2 结果分析

经过模型求解算法计算，路网期望韧性最大值稳定在0.91，对应的除雪作业车辆路径如表4所示。从除雪物资布局优化结果来看，在冰雪天气情景预测信息较为模糊的情况下，物资布局应避免过于集中，应根据情景特征有所侧重地对物资站选址布局。从融雪除雪作业安排优化结果来看，在道路作业前期应多安排融雪剂除雪作业，降雪后期应以机械除雪作业为主。这样合理安排两种作业方式可节约除雪作业成本，避免重复低效作业，有利于提高冰雪天气下城市路网服务能力的快速恢复，增强城市韧性。算例结果证明了本文提出的模型与求解方法对于增强城市路网韧性是有效的。

本文模型中将年度冰雪天气道路保障总预算作为参数处理。显然，总预算额的大小将影响路网恢复工作安排，进而影响该年度冰雪天气下路网期望韧性。为了进一步研究年度道路保障总预算P对该年度冰雪天气下的城市路网期望韧性的影响，本文选取十个不同预算额参数，代入数学模型，运行模型求解算法进行反复运算，得到了该模型下的道路保证预算额与路网期望韧性的帕累托前沿，如图6所示。

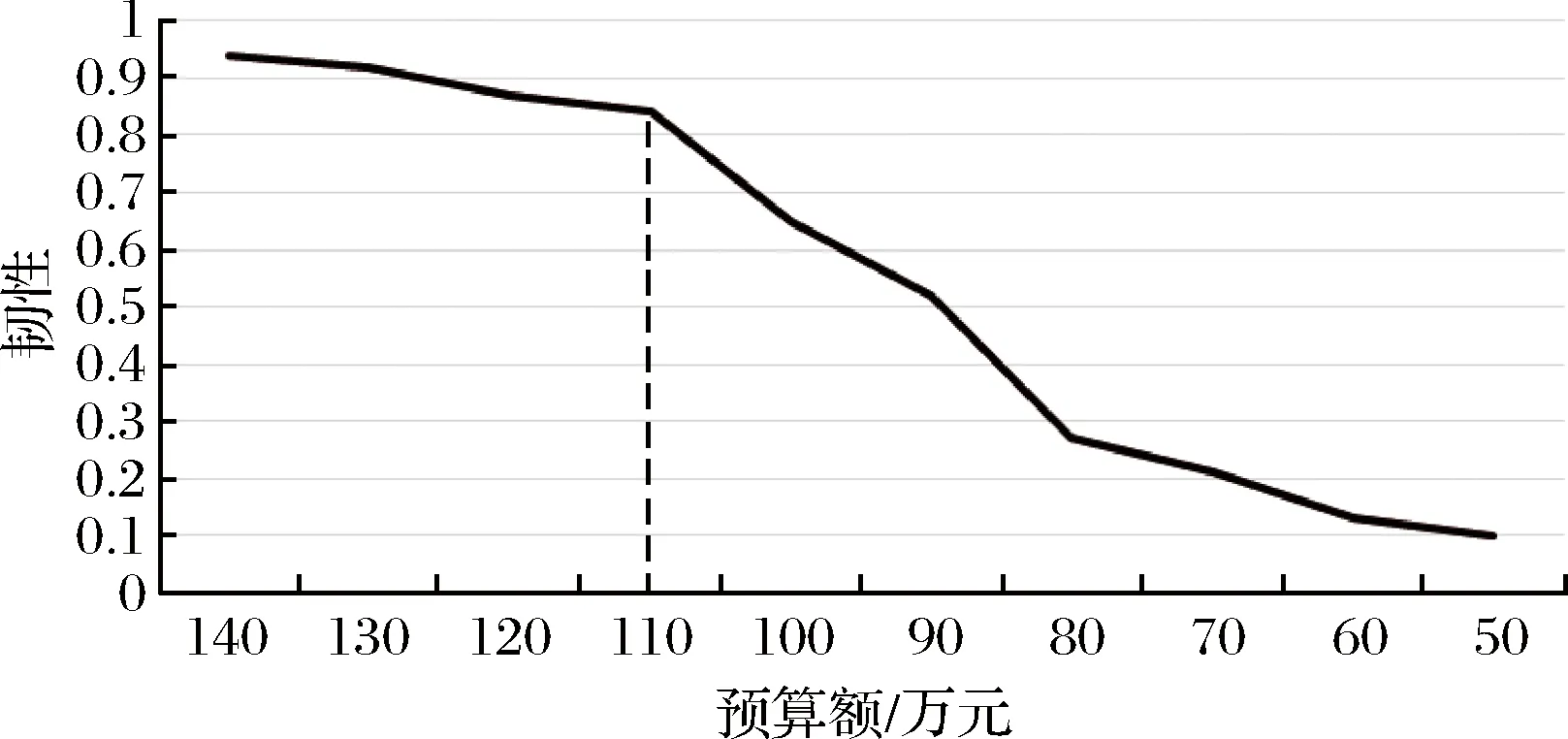
图6 韧性-预算的帕累托前沿

数据结果显示，预算额在140万元至110万元时，路网期望韧性随预算减少而下降缓慢；预算额低于110万元时，韧性下降速度明显加快。而本算例中关键路段的保障费用约为110万元。由此可知，在实际决策中，冰雪天气下的路网保障预算至少应满足关键路段的需求，才能更好的提升路网期望韧性。

6 结语

随着全球气候变暖逐年加剧，冬季的极端冰雪天气频繁发生，对城市基础设施安全构成严重威胁，“韧性城市”受到社会各界的广泛关注。城市道路网络是城市内重要的生命线基础设施，即便是微弱的冰雪天气冲击也可能使其陷入瘫痪。研究如何在冰雪天气来临之前，根据城市历年冬季气象数据布局应急除雪物资并以物资布局为基础制定各天气情景下除雪作业预案，提高城市路网在冰雪天气下的快速恢复能力，具有极高的现实价值。本文从“韧性城市”的视角出发，选取路网中独立路径作为评价对象，以平均车速代表路网对交通参与者的服务能力，考虑了路面积雪厚度对车辆行驶速度的影响，提出冰雪天气下的城市路网系统韧性的度量方法，解决极端冰雪天气不确定信息下的城市路网除雪应急物资布局问题及其除雪作业优化问题；利用冰雪天气离散情景表构建算例进行仿真实验，验证了模型的可行性和恢复策略的有效性。本文充分借助了韧性概念的系统性、全局性的优势进行优化研究，对冬季路网恢复和城市韧性提升决策具有较强的指导意义。

本文在模型中未考虑应急除雪物资中心的容量上限，且对道路恢复的决策只限于铲雪除冰等“硬手段”，未来研究应考虑如何将交通疏导等“软措施”与路面除雪工作相结合，更加有效地降低极端冰雪天气对城市路网运转的不利影响。另外，应当从目前仅加强单个城市基础设施的韧性，扩展到对包含多个城市基础设施的城市生命线系统的恢复韧性优化研究，这样更能体现出韧性概念的系统性、全局性的优点，也将是未来关于城市基础设施韧性的一个研究方向。

[1] 李军,李向阳,张佰尚.自然异动下关键基础设施网络风险研究[J].中国管理科学. 2014, 22(9):66-73.

[2] Fu Liping. Optimizing winter road maintenance operationsn under real-time information[J]. European Journal of Operational Research , 2009,196(1): 332-341.

[3] Dussault B, Golden B, Wasil E. The downhill plow problem with multiple plows[J] Journal of The Operational Research Society ,2014, 65(10):1465-1474.

[4] Muyldermans L, Cattrysse D, Oudheusden D V, et al. Districting for salt spreading operations[J]. European Journal of Operational Research 2002,139(3):521-532.

[5] Muyldermans L, Cattrysse D, Oudheusden D V. District design for arc-routing applications[J]. Journal of the Operational Research Society, 2003,54(11):1209-1221.

[6] Perrier N, Langevin A, Campbell J F. The sector design and assignment problem for snow disposal operations[J].European Journal of Operational,2008,189(2):508-525.

[7] Quirion-Blais O, Langevin A, Lehuede F，et al. Solving the large-scale min-max K-rural postman problem for snow plowing [J]. Networks, 2017,70(3):195-215.

[8] 谢秉磊,李颖.刘敏.带临时补充点的融雪剂撒布车辆路径问题[J]系统工程理论与实践.2016,34(6):1593-1598.

[9] Holling C S. Resilience and stability of ecological systems[J].Annual Review of Ecology and Systematics.1973, 4(4):1-23.

[10] 李亚,翟国方,顾福妹.城市基础设施韧性的定量评估方法研究综述[J].城市发展研究,2016,23(6):113-122.

[11] 高海翔,陈颖,黄少伟,等.配电网韧性及其相关研究进展[J].电力系统自动化，2015,39(3):1-8.

[12] Aven T. On some recent definitions and analysis frameworks for risk, vulnerability, and resilience[J].Risk Analysis,2011,31(4):515-522.

[13] Cen Nan, Sansavini G. A quantitative method for assessing resilience of independent infrastructures[J]. Reliability Engineering and System Safety,2017,157:35-53.

[14] Tran H T, Balchanos M, Domerçant J C,et al. A framework for the quantitative assessment of performance-based system resilience[J].Reliability Engineering & System Safety,2017,158:73-84.

[15] 朱吉双,张宁.可变需求结构下城市路网的通行能力与服务水平模型[J].系统工程理论与实践.2008,6:170-176.

[16] Zhang Weili, Wang Naiyu.Resilience-based risk mitigation for road networks[J].Structural Safety,2016,62:57-65.

[17] Ip W H, Wang Dingwei. Resilience and friability of transportation networks: Evaluation, analysis and optimization[J].IEEE Systems Journal, 2011, 5(2):189-198.

[18] Highway capacity manual[M].Washington D C: Transportation Research Board,2010．

[19] Francis R, Bekera B. A metric and frameworks for resilience analysis of engineered and infrastructure systems[J]. Reliability Engineering and System Safety ,2014,121:90-103.

[20] 张明红,佘廉,耿波.基于情景的结构化突发事件相似度研究[J].中国管理科学. 2017,25(1):151-159.

[21] 刘长石,彭怡,寇纲.震后应急物资配送的模糊定位-路径问题研究[J].中国管理科学. 2016,21(5): 111-118.

[22] 杨锋,梁樑,毕功兵,等.考虑道路特性的多个应急设施选址问题：基于DEA的研究[J].管理评论.2008,20(12): 41-44.

[23] 张敏，张玲.基于失效情景的应急设施选址评估指标体系与模型[J].中国管理科学. 2016,24(11): 129-136.

[24] 于峰,李向阳,刘昭阁. 城市灾害情景下应急案例本体建模与重用[J].管理评论, 2016, 28(8):25-36.