属性集容量确定的夹挤式测度模式及其推算模型

李春好，李孟姣，田 硕

(吉林大学管理学院，吉林 长春 130022)

1 引言

针对建立在属性偏好独立假设基础上的传统多属性决策模型即属性权重固定不变的加权平均模型不能反映决策者关于属性偏好的关联关系问题，Grabisch提出了取代属性权重的属性集容量概念，并在此基础上通过引入Choquet积分算子，建立了适用于属性偏好关联情形的多属性决策模型(下文称作多属性决策Choquet积分模型)[1]。该模型自提出后便受到学术界的高度关注，专家和学者在对其开展应用研究的同时也进行了相关理论扩展研究[2-3]。特别地，赵树平等[2]基于多属性决策Choquet积分模型提出了偏好关联情形下的多属性群决策方法。

需要指出，无论是多属性决策Choquet积分模型还是基于多属性决策Choquet积分模型的多属性群决策方法，在实际决策应用时均可能出现不可行问题。具体地讲，对于属性有n个的多属性决策问题应用多属性决策Choquet积分模型，需要决策者给出的属性集容量个数为指数量级的2n个，因此当n的取值较大时模型会因决策者判断工作过于繁重而失去应用的可行性[4-7]。目前，学术界通常将这种过于繁重的属性集容量判断称为多属性决策Choquet积分模型的指数复杂性难题。

为解决属性集容量判断的指数复杂性难题，Sugeno基于“任意两属性集的交互作用同两属性集容量乘积之比为常数λ”的假设(下文称比例假设)，提出了关于容量判断与推算的λ模糊测度模式(有时也简称为λ模糊测度)[8]。虽然该模式能够明显降低决策者的容量判断工作量(需要决策者判断给出的容量仅为n个)，但受比例假设的影响，相对于多种多样的实际决策问题而言其适用性较差[4,9]。对此问题，武建章、张强进一步指出λ模糊测度模式只能表示一类交互作用(即偏好关联关系要么全部是正向的要么全部是负向的)，因而当决策者的偏好结构中既存在正向交互作用又存在负向交互作用时该模式并不适用[10]。与λ模糊测度模式不同，Grabisch[11]基于“k个以上属性间无交互作用”的假设(下文称无交互作用假设)提出了k-可加模糊测度模式(有时也简称为k-可加模糊测度)。在该模式基础上，学术界结合决策者给出的判断信息构建了多种容量推算模型，如Marichal和Roubens[5]提出的容量推算优化模型等等。然而，k-可加模糊测度模式的容量推算模型有时并没有可行解，因而其决策适用性也会受到限制。对此问题，尽管Grabisch等[6]建议采用k+1-可加模糊测度等高阶可加模糊测度构建模型，但他自己也承认上述做法并不能一定保证引入高阶可加模糊测度后的容量推算模型具有可行解。为发展k-可加模糊测度模式，章玲和周德群[12]通过引入属性间关联矩阵和关联关系阈值λ来推算确定属性集容量。虽然他们所给出的方法仅要求决策者给出属性间的直接关联度及阈值λ，能够降低决策者的判断工作量，但也存在两方面不足。其一，关于属性间关联矩阵没有区分属性关联与属性偏好关联之间的内涵差异。其二，阈值λ需要由专家或决策者凭经验加以设定，因而所推算确定出的属性集容量具有较强的经验随意性。

为解决上述问题，下文以平衡容量判断的数量可操作性和容量推算的准确性为视角，在简要介绍相关基础知识的基础上，提出一种新容量测度模式，即关于容量判断与推算的夹挤式测度模式，并在此基础上给出属性集容量的推算模型，之后采用数值模拟的方式对夹挤式测度模式、λ模糊测度模式、k-可加模糊测度模式进行对比分析，以验证夹挤式测度模式的决策适用性。

2 相关基础知识

设多属性决策问题有n个属性，分别为C1,…,Cn，并将属性全集{C1,…,Cn}记为N；将属性全集N除去属性Ci外的属性集记为N{Ci}，i∈{1,…,n}；将任意属性集A中属性的个数记为|A|；将包含k个属性的属性集容量简称为k阶容量，k∈{1,…,n}。

2.1 容量

容量，又称模糊测度，是一个非负次可加集函数。其定义如下：

定义1[13-14]对于有限属性全集N及其幂集P(N)，若存在集函数μ:P(N)→[0,1]满足：①边界条件，即μ(Ø)=0，μ(N)=1；②单调性条件，即∀A,B⊆P(N)，且A⊆B，有μ(A)≤μ(B)，则称μ为定义在P(N)上的容量。

类似于传统多属性决策模型中属性权重的可操作性内涵解释，Grabisch[1]将属性集容量解释为属性集的重要性或重要程度。此外，由于随着属性个数的增多，需要决策者予以判断给出的容量个数会呈指数性增长，而从容量判断的数量可操作性上看，要求决策者对过多的容量开展判断并不具有具体实施的可操作性，因而如何减少容量判别的个数便成为学术界关于容量确定的难题。

2.2 λ模糊测度模式

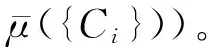
(1)

由于当Sλ=N时有μ(Sλ)=μ(N)=1，因此式(1)可转化为：

(2)

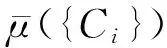
(3)

需要指出，由于λ模糊测度模式建立在比例假设基础上，只能应用于属性间偏好关联关系要么全为正向的要么全为负向的决策问题，而对于属性间偏好关联关系既有正向的又有负向的决策问题，采用式(3)推算出的属性集容量会因误差过大而失去决策的适用性[4,9-10]。

2.3 k-可加模糊测度模式

为减少容量判断的个数，Grabisch[11]通过容量的Möbius变形及无交互作用假设提出了k-可加模糊测度模式。从原理上讲，该模式仅需要决策者判断给出1阶至k阶容量μ(Dk)(Dk⊆P(N)且|Dk|≤k)的判断信息。对于k阶以上的容量μ(Sk)(Sk⊆P(N)且|Sk|>k)，通过无交互作用假设和μ(Dk)的Möbius变形由式(4)予以推算确定：

(4)

其中a(Dk)为容量μ(Dk)的Möbius变形，其表达式为

(5)

在使用k-可加模糊测度模式时，为了尽可能使得容量的推算误差最小化，一般可采用式(6)所示优化模型进行容量推算。

(6)

需要指出，式(6)有时并没有可行解。为此，Grabisch等[6]建议使用k+1-可加模糊测度等高阶可加模糊测度来克服式(6)无解问题。但是，Grabisch等[6]也承认，即使使用高阶可加模糊测度(甚至n-可加模糊测度)，式(6)优化模型也并不能保证一定有解。由此可见，k-可加模糊测度模式并不能保证对任何实际决策问题均适用，尚存在着应用可行性较差的技术缺陷。

3 容量确定的夹挤式测度模式

多属性决策要求决策者判断给出的偏好信息一般有数值信息和序信息两种类型[17]。不同于数值信息的给出需要决策者承受较大的判断压力，采用序信息进行偏好描述对决策者而言其判断压力较小，因而相对于数值信息决策者更易于判断给出其偏好描述的序信息[18-22]。由此并为克服λ模糊测度模式与k-可加模糊测度模式采用人为假设、过于追求容量判断的可操作性而牺牲容量推算准确性的技术不足，下文以平衡容量判断的可操作性与容量推算的准确性为视角，提出一种既能保证容量判断的可操作性又能提高容量推算准确性的新容量测度模式，并在此基础上通过引入决策者较易判断给出的容量序信息构建相应的容量推算模型。新容量测度模式由容量序判断、低阶容量(1阶和2阶容量)数值判断、高阶容量(3阶及3阶以上容量)序的端点容量数值判断和容量推算模型四部分组成。其技术核心是通过确定同阶容量(阶数相同的容量)中的最大值和最小值而将其他同阶容量的取值夹在两个边界值之间，并且通过决策者给出的属性集容量排序将各属性集容量的推算值挤到特定取值区间内。基于上述技术核心，我们将所给出的新容量测度模式称为夹挤式测度模式。

3.1 容量序判断

请决策者按照容量的可操作性定义(即属性集的重要性)对l(l∈{1,…,n-1})阶容量开展容量序判断，并将其由小到大的排序记为RANKn,l。需要指出，当属性个数n较小时，可以直接对l阶容量开展容量序判断；当n取值较大时，为降低决策者的判断难度，首先请决策者按照非常不重要、较不重要、中等程度重要、较重要、非常重要五个等级对l阶容量进行重要程度划分，然后分别对每个重要程度等级内的容量排序，进而得到l阶容量的排序。

3.2 低阶容量数值判断

以1阶容量数值判断为例，其步骤为：首先请决策者相对于属性全集重要性μ(N)=1对RANKn,1排序端点的容量(即1阶容量中的最大容量和最小容量)在[0,1]上赋值，然后请决策者按照RANKn,1对其余1阶容量在两个边界值之间赋值。2阶容量和1阶容量的赋值步骤类似。1阶容量和2阶容量赋值完成后需要检验其是否满足定义1中单调性条件的数量关系。若不满足，则需要重新对其赋值。

3.3 高阶容量序的端点容量值判断

对于3阶及3阶以上容量，请决策者相对于属性全集容量μ(N)=1在[0, 1]上对各阶容量排序RANKn,m(m∈{3,…,n-1})的端点容量(即m阶容量中的最大容量和最小容量)赋值。

3.4 夹挤式容量推算模型

利用决策者给出的容量序信息、低阶容量数值信息、高阶容量序的端点容量数值信息等判断信息，建立如下容量推算模型：

(7)

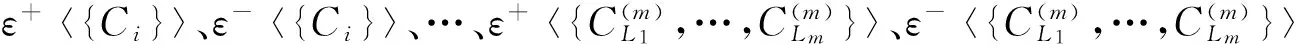
需要强调指出，与k-可加模糊测度模式所依赖的推算模型类似，建立夹挤式容量推算模型的意义在于保证推算出的容量符合定义1的理论关系，并使容量推算误差最小化，从而提高容量推算的准确性。

3.5 夹挤式测度模式的技术优势

4 数值模拟对比分析

数值模拟对比分析旨在通过对属性个数不同的多属性决策问题开展多次模拟，来验证夹挤式测度模式在决策适用性(包括决策应用可行性和容量推算准确性)方面相对于原有容量判断模式的比较优势。

为使模拟对比接近具体决策的实际情况，下文分别按照多属性决策问题有5个属性、7个属性和9个属性共三种情形进行模拟。此外，为保证对比分析更具有一般性，在借鉴Bottomley和Doyle[23]的模拟研究基础上，针对每种情形分别模拟5000次(Bottomley和Doyle[23]中的模拟次数为1000次)。

由于夹挤式测度模式需要决策者判断给出的容量个数略多于2-可加模糊测度，可能会导致前者的容量推算准确性高于后者，因此为更苛刻地检验夹挤式测度模式的容量推算准确性，下文在对比夹挤式测度模式和k-可加模糊测度模式时，不仅将夹挤式测度模式和2-可加模糊测度模式进行对比，而且还将夹挤式测度模式同3-可加模糊测度(需要决策者进行数值判断的容量的个数多于夹挤式测度模式)进行对比。此外，由于在λ模糊测度模式下只要决策者判断给出1阶容量值就能相应地确定出λ*值及各阶容量的推算值，从形式上看该模式对于任何决策问题均具有应用可行性，因此下文在对比夹挤式测度模式和λ模糊测度模式时仅比较两者在容量推算准确性方面的差异。

步骤1：令h=0，hSMP=0，h2=0，h3=0，zSMP,λ=0，zSMP,2=0，zSMP,3=0。

步骤2：使用Matlab中rand函数随机生成一组符合定义1数量关系的基准容量组，并令h=:h+1。

步骤3：将基于基准容量组中1阶至n-1阶属性集容量值得到的各阶容量排序视为决策者基于夹挤式测度模式判断给出的容量序，将基准容量组中的1阶和2阶容量值视为决策者基于夹挤式测度模式判断给出的1阶和2阶容量值，并将基准容量组中m(m∈{3,…,n-1})阶容量排序的端点容量值视为决策者基于夹挤式测度模式判断给出的m阶容量序的端点容量值；类似地，将基准容量组中的1阶容量值视为决策者基于λ模糊测度所给出的1阶容量值；将基准容量组中的1阶和2阶容量值视为决策者基于2-可加模糊测度所给出的1阶和2阶容量值；将基准容量组中的1阶至3阶容量值视为决策者基于3-可加模糊测度所给出的1阶至3阶容量值。

如果Mn在成岩过程中活动性较强，可用Al2O3/(Al2O3+Fe2O3)代替Al2O3/(Al2O3+Fe2O3 +MnO)[11]，另外MnO含量极低，远远低于Al2O3、Fe2O3含量，对最终结果并无影响。研究区硅质岩Al2O3/(Al2O3+Fe2O3)比值为0.39～0.87，平均为0.71，除样品化-49-8其余样品均大于0.5，位于大洋盆地(0.4～0.7)和大陆边缘(0.5～0.9)硅质岩范围内，说明研究区硅质主要形成于大陆边缘，而处于石炭系与泥盆系分界处的样品化-49-8比值0.39，可能形成于大陆边缘到大洋盆地的过渡地带。

步骤4：将决策者基于夹挤式测度模式判断给出的各阶容量序、1阶和2阶容量值、m阶容量序的端点容量值输入到该模式的容量推算模型(见式(7))，并利用matlab中求解线性规划的linprog函数对其求解：若该模型有解(即linprog函数的输出结果中优化指示参数exitflag值为1)，则令hSMP=:hSMP+1，并计算推算出的1阶至n-1阶容量值与基准容量组中相应容量值的均方根值(将其记为RMSSMP)；若该模型无解(即exitflag≠1)则直接进入步骤5。

步骤5：将决策者基于λ模糊测度模式判断给出的1阶容量值输入式(2)计算λ*值，然后由其容量推算模型(见式(3))推算得出2阶至n-1阶容量值，最后计算推算得出的2阶至n-1阶容量值与基准容量组中相应容量值的均方根值(将其记为RMSλ)。

步骤6：将决策者基于2-可加模糊测度模式判断给出的1阶和2阶容量值输入该模式下的推算模型(见式(6))，并利用matlab中的linprog函数对该模型求解：若该模型有解，则令h2=:h2+1，并计算其推算出的1阶至n-1阶容量值与基准容量组中相应容量值的均方根值(将其记为RMS2)；若该模型无解，则直接进入步骤7。

步骤7：将决策者基于3-可加模糊测度判断给出的1阶至3阶容量值输入该模式下的推算模型(见式(6))，并利用matlab中的linprog函数对该模型求解：若该模型有解，则令h3=:h3+1，并计算推算出的1阶至n-1阶容量值与基准容量组中相应容量值的均方根值(将其记为RMS3)；若该模型无解，则直接进入步骤8。

步骤8：若步骤4中夹挤式测度模式的推算模型有解，则令zSMP,λ=:zSMP,λ+1，并计算RMSSMP减RMSλ的值(将其记为ΔRMSSMP,λ)，否则直接进入步骤9。

步骤9：若步骤4中夹挤式测度模式的推算模型有解，同时步骤6中2-可加模糊测度的推算模型也有解，则令zSMP,2=:zSMP,2+1，并计算RMSSMP减RMS2的值(将其记为ΔRMSSMP,2)，否则进入步骤10。

步骤10：若步骤4中夹挤式测度模式的推算模型有解，同时步骤7中3-可加模糊测度的推算模型也有解，则令zSMP,3=:zSMP,3+1，并计算RMSSMP减RMS3的值(将其记为ΔRMSSMP,3)，否则直接进入步骤11。

步骤12：对夹挤式测度模式、λ模糊测度模式、k-可加模糊测度模式的推算模型在5000次模拟中能够给出最优解的次数(即hSMP、h2、h3)及均方根之差(即ΔRMSSMP,λ、ΔRMSSMP,2、ΔRMSSMP,3)进行统计。

经上述步骤，最终给出的h值为对模拟次数的计数，hSMP值、h2值、h3值为对夹挤式测度模式、2-可加模糊测度模式、3-可加模糊测度模式分别对应的容量推算模型求得最优解次数的计数，zSMP,λ值为对夹挤式测度模式与λ模糊测度模式容量推算准确性对比次数的计数，zSMP,2值为对夹挤式模糊测度模式与2-可加模糊测度模式容量推算准确性对比次数的计数，zSMP,3值为对夹挤式测度模式与3-可加模糊测度模式容量推算准确性对比次数的计数。经统计，在5000次模拟中，各种容量测度模式(不含λ模糊测度模式)能够给出最优解的次数及比例如下表1所示；关于夹挤式测度模式对应的均方根值与其他两种容量测度模式对应的均方根值之差的统计结果如下表2所示。

表1 夹挤式测度模式、k-可加模糊测度在5000次模拟中得到最优解次数及比例

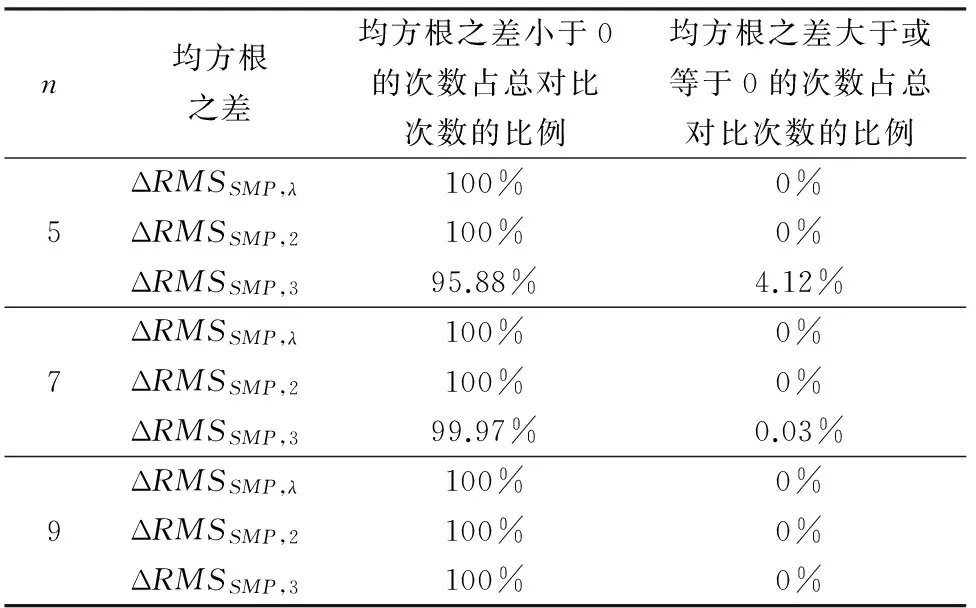
表2 夹挤式测度模式相对于λ模糊测度和k-可加模糊测度的均方根之差

由表1可知：尽管随着属性个数的增加(即属性个数由5个增加为9个)，2-可加模糊测度模式和3-可加模糊测度模式获得最优解的比例(即模式可行的比例)呈现出先减后增的态势，但它们均没有保证所采用的容量推算模型对每次模拟均可行。而夹挤式测度模式针对三种模拟情形无论属性个数怎样变化每次模拟均给出了最优解，没有类似于k-可加模糊测度模式出现不可行问题。这表明，夹挤式测度模式相对于k-可加模糊测度模式具有更高的决策应用可行性。由表2可知：在绝大多数情况下，夹挤式测度模式对应的均方根值不仅小于λ模糊测度模式、2-可加模糊测度模式对应的均方根值，而且也小于3-可加模糊测度模式所对应的均方根值。这表明夹挤式测度模式要比λ模糊测度模式、k-可加模糊测度模式具有更高的容量推算准确性。综上可知，夹挤式模糊测度模式在决策适用性上明显优于λ模糊测度模式和k-可加模糊测度模式。

5 结语

现有文献针对属性集容量确定的指数复杂性难题提出的容量测度模式(即λ模糊测度模式和k-可加模糊测度模式)，虽然在一定程度上提高了决策者容量判断的可操作性，但由于其中采用了较为武断的人为假设(即比例假设和无交互作用假设)，因而在实际决策应用中存在着适用性差的缺陷。为此，上文以平衡容量判断的可操作性和容量推算的准确性为视角给出了一种新容量确定模式，即夹挤式测度模式，并在此基础上通过引入决策者较易判断给出的容量序信息构建了相应的容量推算模型。新模式具有如下两方面技术优势：其一，从降低容量判断的指数复杂性上看，具有与2-可加模糊测度模式相近的应用可操作性；其二，不再引入武断的人为假设，而是直接采用更符合决策者偏好描述的容量序信息及序端点容量值信息，因而相对于λ模糊测度模式和k-可加模糊测度模式具有更高的容量推算准确性。基于数值模拟的对比分析表明，夹挤式测度模式不仅在应用可行性上高于k-可加模糊测度模式，而且从容量推算的准确性上看也明显优于λ模糊测度模式和k-可加模糊测度模式。综上所述，夹挤式测度模式较之于λ模糊测度模式和k-可加模糊测度模式具有更强的决策适用性。

需要强调指出，与k-可加模糊测度模式仅适用于k个及k个以下属性间偏好具有交互作用而在k个以上属性间偏好相互独立的决策场合不同，也与λ模糊测度模式仅适用于偏好关联关系要么全是正向的要么全是负向的决策场合不同，夹挤式测度模式因其中不再引入人为假设，只要决策者能够判断给出容量序、低阶容量值、高阶容量序端点容量值，它便可以适用于具有各种偏好关联关系的决策场合。换言之，夹挤式测度模式具有逾越λ模糊测度模式和k-可加模糊测度模式仅适用于特殊场合的决策应用一般性。

[1] Grabisch M. The application of fuzzy integrals in multicriteria decision making[J]. European Journal of Operational Research, 1996, 89(3):445-456.

[2] 赵树平,梁昌勇,罗大伟.基于VIKOR和诱导广义直觉梯形模糊Choquet积分算子的多属性群决策方法[J].中国管理科学, 2016, 24(6): 132-142.

[3] 常志鹏,程龙生.灰模糊积分关联度决策模型[J].中国管理科学, 2015, 23(11): 105-111.

[4] Grabisch M, Labreuche C. A decade of application of the Choquet and Sugeno integrals in multi-criteria decision aid[J]. Annals Operations Research, 2010, 175(1):247-286.

[5] Marichal J L, Roubens M. Determination of weights of interacting criteria from a reference set[J]. European Journal of Operational Research, 2000, 124(3):641-650.

[6] Grabisch M, Kojadinovic I, Meyer P. A review of methods for capacity identification in Choquet integral based multi-attribute utility theory： Applications of the Kappalab R package[J]. European Journal of Operational Research, 2008, 186(2): 766-785.

[7] Anath R K, Maznah M K, Engku M N E A B. A short survey on the usage of Choquet integral and its associated fuzzy measure in multiple attribute analysis[J]. Procedia Computer Science, 2015, 59:427-434.

[8] Sugeno M. Theory of integral and its applications[D]. Tokyo: Tokyo Institute of Technology,1974.

[9] David S, Martin H. Dynamic classifier aggregation using interaction-sensitive fuzzy measures[J]. Fuzzy Sets and Systems, 2015, 270:25-52.

[10] 武建章, 张强. 基于2-可加模糊测度的多准则决策方法[J]. 系统工程理论与实践, 2010, 30(7):1229-1237.

[11] Grabisch M. K-order additive discrete fuzzy measure and their representation[J]. Fuzzy Sets and Systems, 1997, 92(2): 167-189.

[12] 章玲,周德群.基于k-可加模糊测度的多属性决策分析[J].管理科学学报, 2008, 11(6): 18-24.

[13] Yager R R. Modeling multi-criteria objective functions using fuzzy measure[J], Information Fusion, 2015, 29(3):105-111.

[14] Wu Yunna, Geng Shuai, Xu Hu, et al. Study of decision framework of wind farm project plan selection under intuitionistic fuzzy set and fuzzy measure environment[J]. Energy Conversion and Management, 2014, 87:274-284.

[15] Yang J L, Chiu H N, Tzeng G H, et al. Vendor selection by integrated fuzzy MCDM techniques with independent and interdependent relationships[J]. Information Sciences, 2008, 178(21):4166-4183.

[16] Chen T Y, Wang J C. Identification ofλ-fuzzy measures using sampling design and genetic algorithms[J]. Fuzzy Sets and Systems, 2001, 123(1):321-341.

[17] Xu Xiaozhan, Martel J M, Lamond B F. A multiple criteria ranking procedure based on distance between partial preorders[J]. European Journal of Operational Research, 2001, 133(1):69-81.

[18] Lahdelma R, Miettinen K, Salminen P. Ordinal criteria in stochastic multicriteria acceptability analysis (SMAA)[J]. European Journal of Operational Research, 2003, 147(1):117-127.

[19] Punkka A, Salo A. Preference programming with incomplete ordinal information[J]. European Journal of Operational Research, 2013, 231(1):141-150.

[20] Sarabando P, Dias L C. Simple procedures of choice in multicriteria problems without precise information about the alternatives’ values[J]. Computer and Operations Research, 2010, 37(12):2239-2247.

[21] Fitousi D. Dissociating between cardinal and ordinal and between the value and size magnitudes of coins[J]. Psychonomic Bulletin & Review, 2010, 17(6):889-894.

[22] Ahn B S, Park K S. Comparing methods for multiattribute decision making with ordinal weights[J]. Computers & Operations Research, 2008, 35(5):1660-1670.

[23] Bottomley P A, Doyle J R. A comparison of three weight elicitation methods: Good, better, and best[J]. Omega, 2001, 29(6): 553-560.

[24] Saaty T L. The analytic hierarchy process[M]. New York: McGraw-Hill, 1980.

[25] Saaty T L. A scaling method for priorities in hierarchical structures[J]. Journal of Mathematical Psychology, 1977, 15(3): 234-281.