基于Logistic生长方程—马尔可夫模型的港口投资风险测度
2018-03-29李电生张腾飞
李电生,张腾飞
(中国海洋大学经济学院,山东 青岛 266100)
1 引言
随着习总书记“一带一路”战略构想的提出,港口作为“一带一路”的核心节点受到国内外学者关注,同时随着世界经济和我国经济的深入调整,我国经济从高速增长逐渐向经济新常态发展转变,港口的发展也需要相应的调整和转变,传统的港口投资模式正面临着潜在风险,港口转型升级成为必然要求,因此科学有效地预测港口投资风险,对港口投资和管理有着极其重要的价值。
风险通常分为内生性风险和外生性风险。内生性风险是企业经营过程中存在的风险,国内外学者对港口的内生性风险进行了一系列研究,主要从技术手段、方法模型创新、投资决策、管理经营等方面进行深入研究。比如Frankel[1]分析港口和航运项目决策后的风险评估,充分考虑到需求、成本和技术的不确定性带来的风险,从项目决策后的视角分析风险因素,没有分析港口和航运在投资之前是否存在风险。van Ham等[2]定性分析港口中存在的风险,通过设计公私合营的模式来规避港口运营中的风险。Lam等[3]研究亚洲港口运营风险,采用风险矩阵得出可能性与严重性的相关关系,并对港口出现不可预测风险进行分类。Asteris等[4]分析出英国集装箱港口市场投资规模扩大,需要根据市场需求进行投资和公平竞争,集装箱港口投资不能只依赖于政府调控,从市场需求角度降低投资风险。投资行为的发生导致事件的不确定性,进而产生一定的风险,一些学者从风险事件的根源入手即投资角度,降低风险发生的概率。比如Koh[5]评估集装箱港口投资方案与风险,得出最优投资决策,但没有从度量投资风险的大小值角度入手。Rodrigue等[6]分析了港口投资风险与技术、市场以及金融等存在密切内在联系,并重点从金融化视角研究港口和海运中的风险,通过金融与港口相结合更好的降低经济波动给港口带来的风险。Simkins等[7]分析在港口投资决策中,标称值会误导投资决策的制定尤其是在经济通货膨胀期,而实际值才是投资决策的依据,并能够降低港口的投资风险。从上面这些文献可知,对于港口风险的探讨,无论是采用何种研究方法,还是研究角度变化,港口的风险研究均侧重于经营、管理等方面,很少涉及宏观经济带来的外生性风险。
外生性风险是指受宏观经济影响较大的系统性风险。改革开放后我国经济高速增长,尤其是加入世界贸易组织(WTO)后我国对外贸易得到飞速发展,港口也相应的得到快速发展,港口投资风险没有受到业界和学者足够重视。但随着我国经济结构的调整,经济高速增长带动大规模港口投资时期已经过去,研究外生性港口投资风险对推动港口转型升级具有重要的现实意义。
目前对于外生性投资风险研究,主要集中在金融、保险等领域,与国家宏观经济变化密切相关,易受到经济波动、政策调整的影响较大,因此成为风险研究者们的青睐。目前这类文献研究较多,典型的文献主要有,Chen[8]研究了经济周期内金融市场的投资问题,使用马尔可夫切换模型预测经济增长状态转折点,为金融市场投资规避风险。王春峰等[9]针对现有的风险价值模型(VaR)计算中缺陷,创新性地提出了一种基于马尔科夫链蒙特卡洛模拟的VaR计算方法,以克服传统蒙特卡洛模拟的高维、静态性缺陷,提高风险度量精度,在金融风险预测中广泛应用。Siu等[10]将多元马尔可夫模型运用到信用风险度量中,将历史数据纳入风险评级当中,建立了经验转换矩阵,得到了预期度量效果。高金余等[11]通过马尔可夫切换模型较好的刻画了不同时期股市波动的阶段性特征。杨继平等[12]为了更精确估计结构转换的我国股市收益率波动的特征,把广义自回归条件异方差(GARCH)模型及GARCH的三种改进模型与马尔可夫转换模型结合,最后比较各模型估计的准确率。陈守东等[13]在系统性金融风险度量中引入极值理论,采用极端分位数回归技术分析我国33家上市金融机构对金融系统风险的影响。Liang Xue等[14]研究信用违约风险中的交易风险,并通过连接函数(Copula)分析交易双方相关关系,结合马尔可夫模型预测违约风险状态。
综上所述,由于金融风险具有发生频率高、周期短、与经济波动变化较为明显等特点而受到广泛重视,而港口的外生性投资风险具有一定的独特性,因具有投资金额大、潜伏性周期长、受经济波动影响大和短期不易爆发等特点,因此港口外生性投资风险研究相对较少。黄杰[15]分析出英国、美国以及日本等发达国家的港口投资建设已经进入成熟期,这些发达国家大型港口投资项目建设逐渐减少,国外学者对国外港口投资风险研究较少。而我国高度关注港口对经济的贡献率,忽视经济发展水平对港口规模需求的约束作用,同时我国经济的高速增长带动了港口的发展,使地方政府和港口企业淡化了港口投资的风险意识。
国内学者对我国港口的研究主要集中在港口与区域的互动发展、港口经营管理以及港口间竞争与合作三个层面。其中港口与区域协调发展方面的研究文献有,钟铭等[16]研究了港口与经济腹地的协调发展问题。王洪青等[17]发现一元三次非线性方程模型符合宁波港口与腹地间经济关系,并且对腹地经济贡献弹性有U型特征。而港口的经营管理主要侧重在港口效率测度方面,这类文献相对较多,主要的文献有,李电生等[18]对港口进行效率测度,解决港口设施设备经营管理问题。张小蒂等[19]对中国主要港口三个层次方面进行效率测度,得出投入拥挤与产出不足是港口效率低下主要成因。最后一个层面是港口间的合作竞争,从既有的文献看合作与竞争相辅相成,比如,汪传旭等[20]采用区域港口合作竞争模型研究了港口协调发展问题。丁国蕾等[21]分析上海港、宁波舟山等九大主要港口,认为港口间存在长期均衡关系。以上学者从不同角度和层面研究了港口的发展问题。
从既有文献可知,港口投资风险问题很少受到学者关注,因此这类文献的研究相对缺乏,这与港口独特的外生性投资风险特点有直接关系。2016年7月中国科学院预测科学研究中心发布了“2016年全球Top20集装箱港口预测报告”,报告分析了集装箱吞吐量在缓慢增长的同时,也指出我国港口产能过剩问题开始显现,港口投资风险需引起重视。
本文主要贡献如下:世界经济和我国经济的深入调整,港口也从高速增长逐渐趋近平稳,通过梳理我国港口研究和发展过程,提出了港口产能过剩引发外生性投资风险问题。由于港口的发展同中国经济发展相似,呈现非常明显的非线性发展特点,这样采用传统的单一模型很难刻画这一现实问题。为此,本文首次构造了Logistic生长方程—马尔可夫组合模型,通过Logistic生长方程生成马尔可夫模型所需要的状态参数,在此基础上构造风险转移概率矩阵,有效的解决了港口投资风险的测度问题。本文的研究结果显示港口投资风险在2016开始显现,并将持续较长一段时期。表明我国港口正处在转型升级的关键时期,需加快从外延式扩张向内涵式发展转变,从粗放式到精细化管理转变,港口业务结构优化调整,码头资源重新配置。
2 港口投资风险度量模型的选择与构建
2.1 模型的选择
目前研究外生性风险的方法主要有网络模型、Copula函数与蒙特卡洛等。隋聪等[22]通过网络模型研究银行系统性风险的因素,把违约银行数量或违约银行比率作为衡量风险的指标,但在风险度量中缺少系统性的方法。张晨等[23]用Copula函数度量碳金融市场风险多因子的相关性,Copula函数可以描述非线性、非对称问题,但很难描述随机动态过程,单纯用静态的相关性研究问题也存在缺陷。吴建华等[24]使用蒙特卡洛方法数值分析预期回收率和违约风险之间内在关系,蒙特卡洛方法可以处理某个随机变量的数学期望,但仍然存在高维静态不足等问题。
而马尔可夫模型处理问题时能较好地刻画出系统状态从一个阶段到另一个阶段的演化发展过程,通过状态转移概率矩阵预测系统的变化。但马尔可夫模型在某些问题上无法直接获得状态参数,需要借助其他模型对原始数据进行预处理。如Ramchand等[25]通过SWARCH方法对数据指标预处理,将处理的数据序列结合马尔可夫模型,并估计和预测股市的波动率。罗平等[26]通过多元回归模型解决分类变量与连续变量,与马尔可夫模型组合确定每一个土地利用单元转移概率,进而实现对空间分布的预测。张桦等[27]根据变压器故障机理的复杂性特征,提出马尔可夫过程的状态评估模型,运用熵权模糊计算法量化变压器设备风险等级,构造风险评价矩阵。上述论文针对特定的问题选取了不同的方法组合,解决了相应地问题。本文通过Logistic生长方程与马尔可夫模型组合,弥补了马尔可夫模型的不足。
2.2 基于Logistic生长方程的港口吞吐量增长率预测
从我国GDP增长趋势来看,经济发展水平经历高速增长后逐渐趋于减缓,最后经济增长速度将会达到平衡状态。这充分说明了我国经济发展趋势与Logistic生长模型是相吻合的。与此同时港口的吞吐量变化与经济发展水平密切相关,其变化趋势与我国经济发展水平是相一致。因此用Logistic模型预测我国港口吞吐量变化趋势。
1)本文采用Logistic生长模型研究我国沿海港口吞吐量增长率的变化趋势。Logistic生长方程的微分形式为:
(1)
式中z为种群数量即港口吞吐量增长率,t为时间即不同年份,r为港口吞吐量瞬时增长率,q为常数,表示经济环境最大容纳量。
从Logistic生长方程的一阶导数和二阶导数可以看出Logistic方程的轨迹是一种s形曲线。同时港口吞吐量随着我国经济变化也呈现出s曲线特征,即在开始时港口吞吐量基数较小,则增长速度较慢,中间段港口吞吐量基数达到一定规模且整体的生存空间最大,即港口承受能力最大,因此增长速度较快,末段时间港口吞吐量达到环境最大容量时候其生存空间减少,因此增长速度越来越慢,直至趋近于0,最后达到平衡状态。
为确定Logistic生长方程中z变量的计算公式,在这里首先运用灰色系统理论的方法确定Logistic模型的参数,然后再对Logistic模型的微分形式进行求解。
2)以我国沿海港口吞吐量变化率数据为基础的Logistic模型,首先令a=r,b=r/q将其代入(1)式中,则有:
(2)
按照灰色系统建模的方法则有:
(3)
其中,
B=
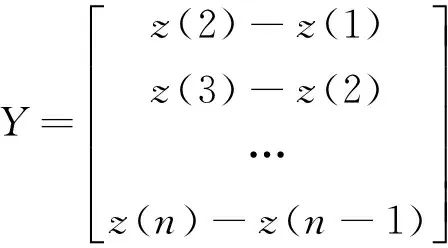
(4)
将参数a,b代入(2)式,解微分方程可得:
z(t)=a·z(1)/(b·z(t0)+(a-b·z(t0))·e-a(t-t0))
(5)
其中z(t)表示t时间港口吞吐量增长率,t0表示初始时间的年份。
离散形式可以表述为:
z(t)=a·z(1)/(b·z(1)+(a-b·z(1))·e-at(i))
(6)
3)精度检验:常用的精度检验方法有关联度法和后验差法,本文采用后验差对模型拟合精度进行评价,主要通过后验差比值c与小误差概率p判断模型精度。后验差检验的具体检验过程见附录1:
(7)
②计算小误差概率p:
(8)
2.3 基于马尔可夫模型的风险转移概率矩阵构造
主要通过观测港口实际投资风险状态预测在未来阶段的港口投资风险状态发生概率,为把投资风险定量化处理,这里给出一个港口投资风险值的定义,即港口投资风险值是港口吞吐量增长率与港口通过能力增长率的比值R。根据港口投资风险值历史数据的划分来构造转移概率矩阵。
首先需要Logistic生长模型预测港口吞吐量增长率,作为给出定义中的投资风险值的一个变量,通过Logistic生长方程生成马尔可夫模型所需要的状态参数,即 Logistic生长模型预测港口吞吐量增长率,然后计算所有观测年份与预测年份的港口吞吐量增长率与港口通过能力增长率的比值建立投资风险值R。然后需要通过聚类分析方法将不同年份对应的投资风险值划分为若干个不同的风险等级,最后采用马尔可夫模型将不同的风险等级之间状态转换过程构造出风险转移概率矩阵。聚类分析方法划分风险状态等级具体详见附录2。

(9)

(10)
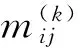
其中港口投资风险转移概率具有以下性质:
(11)
(12)
3 实证分析
本文采用风险度量值R来衡量港口投资风险所处状态程度,港口风险度量值R是指港口吞吐量增长率与港口通过能力增长率的比值,比值R越大表明港口吞吐量增长速度大于港口通过能力增长速度,港口投资风险越小,反之越大。其中港口通过能力与港口吞吐量数据获取来源于《交通部沿海港口通过能力核查报告》和《中国交通信息统计中心》。
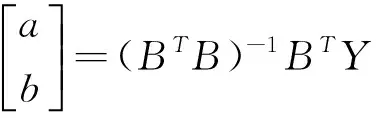
s(t)=a·s(1)/(b·s(1)+(a-b·s(1)·e-at(i))。
整理出的预测吞吐量增长率函数形式为:
s(i)=0.0291/(0.2544/e(0.2646·t(i))+0.0102)其Matlab编程得到预测结果如图1,及港口吞吐量变化预测如图2所示。

图1 港口吞吐量年增长率预测
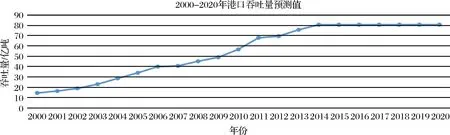
图2 港口吞吐量年增长值预测
运用后验差检验法对港口吞吐量增长率的拟合结果进行检验,得到检验参数c小于0.35 ,p大于0.95对照表6,说明拟合精度较高,应用Logistic生长模型具有较高可靠性;从图1中我们可以看出:吞吐量增长率经历2001至2004年和2007至2011年两个阶段高速增长后,在2013年之后一段时间增长率一直趋于下降,逐步达到平衡状态,这和我国经济发展过程总体是相适应的。从图2可以得出:港口吞吐量增长具有s型曲线特征,从2000到2014年增长较快,然而在经历高速增长后达到一个接近饱和的状态,此时2015年后吞吐量变化将会比较稳定。
根据交通部统计年鉴计算1985—2014年数据与2015—2017年预测数据,最后确定1985至2017年的投资风险值,将风险值大小用聚类划分状态,根据需要确定分类数,系统自动确定初始聚类中心,迭代27次达到收敛标准,确定最终聚类中心以及聚类分级标准,自动形成六个等级标准,1代表风险等级最低,6代表风险等级最高,如表1所示。先计算投资风险值R,再进行状态划分,最后确定样本数据的状态等级,由于投资风险值与风险状态等级可以合并在同一张表中,故把投资风险状态分级标准作为表1,为了清楚表达不同年份的投资风险值处在何种风险状态,构建表2。

表1 投资风险状态分级标准

表2 1985-2017年我国沿海港口投资风险值、风险状态等级
数据来源:交通部沿海港口通过能力核查报告。
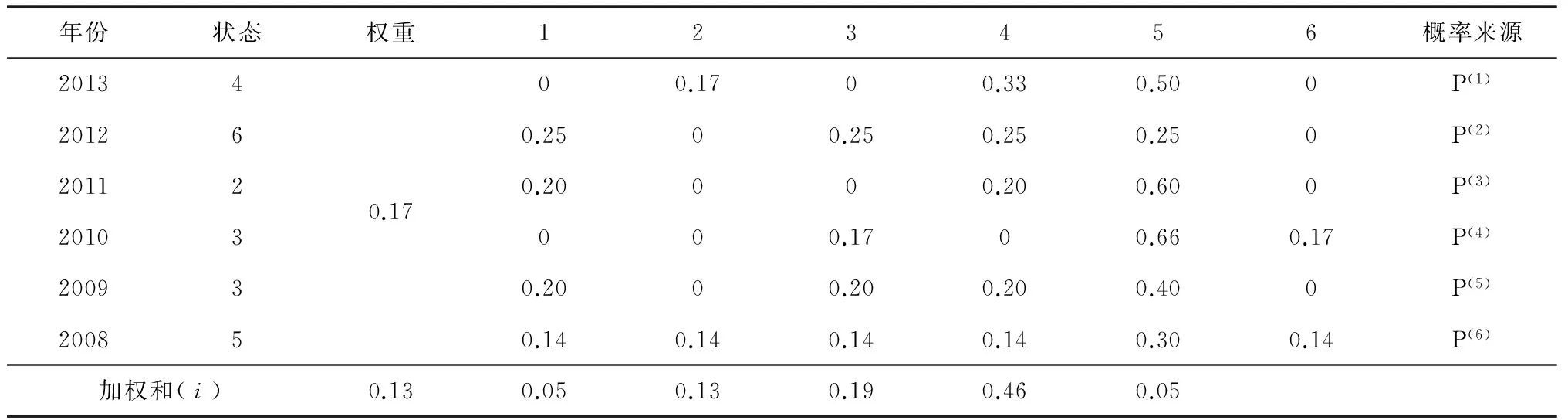
表3 2014年港口投资风险状态等级的预测
通过实际观测数据以及预测数据进行计算,并构造系统六步状态转移概率矩阵,矩阵各元素都是非负的,并且各行元素之和等于1,各元素用概率表示,在一定条件下是互相转移的,其中位于矩阵中第i行与第j列交叉点上的元素是所得概率,根据马尔可夫模型六步转移概率矩阵计算结果如下所示(结果保留两位小数)。
根据投资风险六步状态转移概率矩阵,通过加权马尔可夫模型预测未来一段时间内的投资风险状态空间。针对每一年的风险状态等级,都相对应的存在不同的风险相互转移概率值,但六步转移概率值为1,正如表3所示。为了预测某一年的风险概率,需要该年之前的六年风险状态等级数据作基础,而预测该年的风险状态理论上只存在这六种情况,所以在此把权重系数设置为六种可能状态概率的平均值即权重系数约为0.17。对2014年实际风险状态进行验证以及2020年、2025年的风险状态预测,计算结果如表3、4、5所示。
表3分析得出结论,i=0.46时加权概率值最大,此时对应的风险状态等级为5,即加权马尔可夫模型预测2014年的风险状态与实际观测的风险状态(表2所示)相一致,表明了马尔可夫模型预测结果具有较高的可靠性和稳定性。由马尔可夫模型确定的等级标准,其等级数值越大代表风险越大,同样由表4和5分析可知,2020和2025年港口投资风险状态等级分别为6级和5级,表明具有相对较高的投资风险。
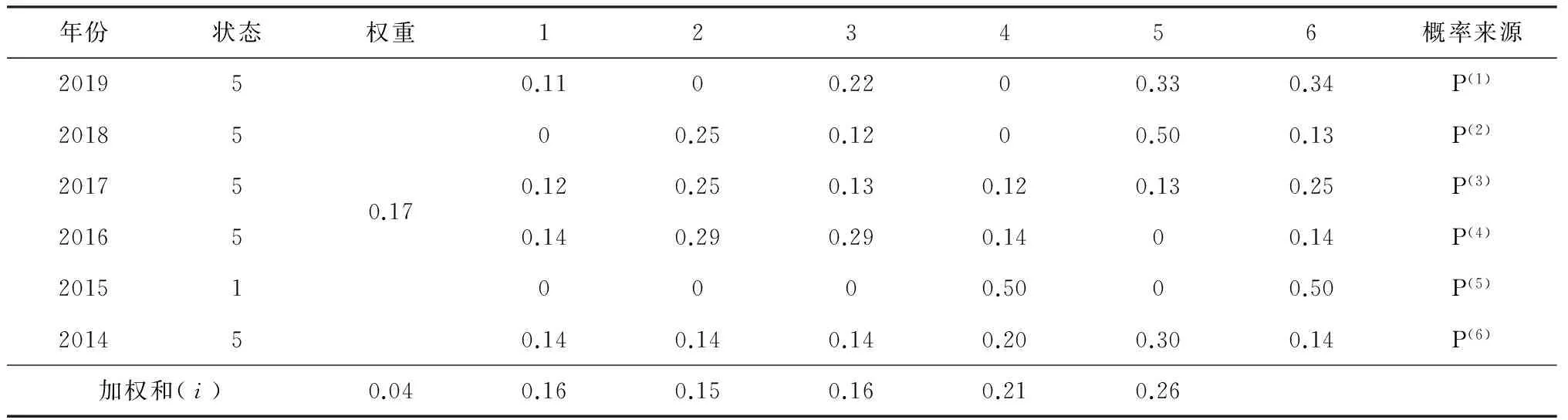
表4 2020年港口投资风险状态等级的预测
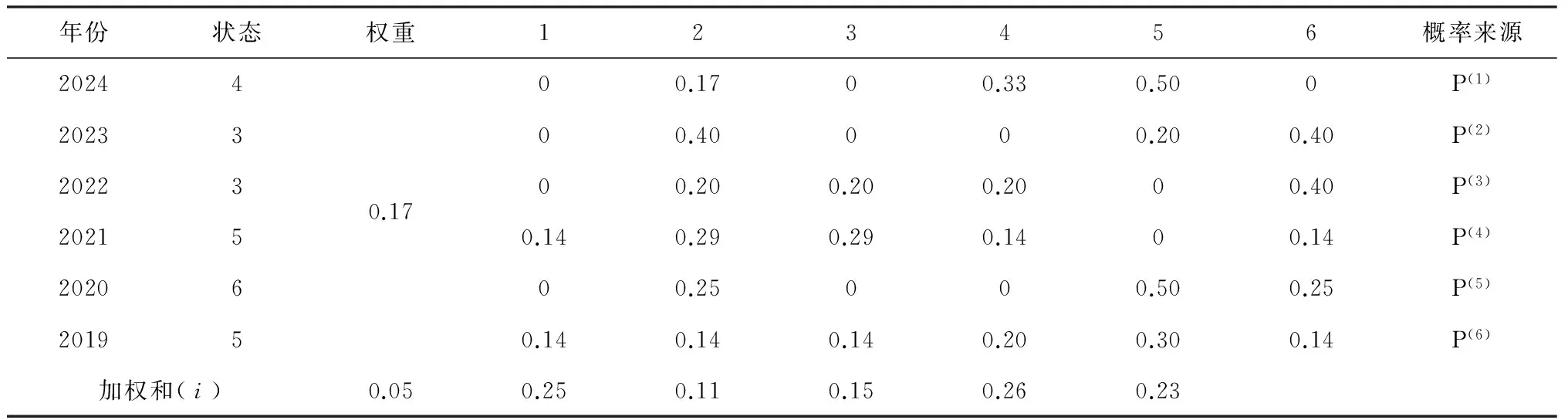
表5 2025年港口投资风险状态等级的预测

表6 拟合精度等级
同理可以预测出2018—2025年的风险状态等级依次为5、5、6、5、3、3、4、5,如图3所示。从图3可以看出,未来我国港口投资风险的整体形式居高不下,由于港口投资属于重资产项目回收期较长,目前继续对港口投资必然存在很大风险。
造成港口投资风险居高不下的原因有:2005—2008年之间,随着经济的飞速发展,港口码头的建设进入新的高潮,港口吞吐量通过能力年均增长率为0.16,而港口实际吞吐量年均增长率为0.12,同比高出4个百分点,这种较大力度的港口投资建设,给港口的发展埋下了风险隐患。由于2008年金融危机的爆发,港口在2009与2010年港口投资建设出现短暂的调整,港口通过能力增长率与吞吐量实际增长率基本平衡。
受金融危机的影响,政府出台了一系列刺激经济的措施,并取得了一定的效果,在2011—2014年港口投资建设又达到了一个新的高度,通过能力增长率高出实际吞吐量增长率2个百分点,并且在建和规划审批中的港口码头泊位100多个,同比增长2.5个百分点,造成了港口事实上的产能过剩。经济新常态下,随着“三去一降一补”、“供给侧改革”等政策的出台,我国经济一直处在下行期,受经济波动影响较大的港口业面临发展瓶颈,低附加价值的大宗物资贸易量大幅下滑,铁矿石、煤炭等主要货种旺季不旺,其港口吞吐量必然增长缓慢,一些大宗商品依赖程度较大的北方港口,全年出现了负增长,直接影响了整体港口货物吞吐量,2015年全年吞吐量仅增长1.1%,较去年缩水4.6个百分点,其中煤炭及其制品吞吐量增长率为负7.3%。随着国家推行创新发展机制,以高新技术产品、机电产品等高附加值的集装箱吞吐量增长较快,2015年集装箱吞吐量增长4.1%,但集装箱吞吐量只占港口总吞吐量的19%,大幅下滑的煤炭、铁矿石等大宗货物占港口总吞吐量的58%,同时这些高附加值的货物具有体积小、重量轻、价值大的特点,所以造成港口吞吐量的规模很难增长,并且开始出现下降态势。
经济深度调整导致港口投资风险在2016年后逐渐显现出来,使得投资回收期与投资风险发生期相一致,投资风险会在较长一段时间内存在。而通过本文预测的未来投资风险状态等级都处在3至6级之间,这里认为风险等级达到4级以上即视为具有较高的投资风险。值得注意的是,未来我国需要适当降低港口建设规模,港口投资风险才会逐步地降低。
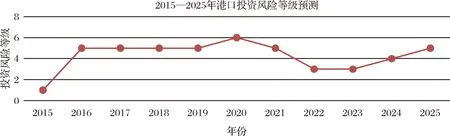
图3 2015—2025年港口投资风险状态等级
4 结语
本文首先应用Logistic生长模型预测港口吞吐量增长率,然后计算港口吞吐量增长率与港口综合通过能力增长率比值,建立港口投资风险值R,最后通过马尔可夫模型模拟预测港口投资风险的转移概率,使得投资风险预测结果具有较强的科学性和准确度。Logistic生长模型预测港口吞吐量增长率一直趋于下降,与我国转型时期的经济发展要求同步,通过马尔可夫模型预测出未来港口投资风险转移到风险等级较高的状态,表明我国港口投资目前存在巨大的潜在风险。由于大型港口投资项目建设期和回收期较长,投资规模大短期内难以回收的特点,同时我国又处在转型时期,尽管进出口仍在小幅增长,但在2016年后风险会突显出来,因此现在对港口投资需慎重而行。
改革开放后我国港口承载力从严重不足变为基本满足经济需求,到现在经济发展放缓港口建设出现过剩,对港口规模和数量过度扩张只能导致资源严重浪费和加剧港口间恶性竞争,片面关注港口建设规模对经济总量的贡献率,忽视我国经济发展水平对港口建设规模的需求度,从而加大对港口投资过剩调控的难度。基于实证分析结果,本文形成以下政策建议:1当前对港口建设发展模式已经不可持续,那么港口未来发展方向需要从外延式扩张向内涵式发展道路转变,更多通过市场配置手段实现港口资源整合与协同发展,2货种结构与经营水平之间关系不协调,导致吞吐量与经济效益严重脱节,优化港口业务结构,重新配置港口码头资源,3港口间也需要进一步形成分工明确,喂给港、支线港和枢纽港层次合理的发展体系,进而提升我国港口综合效率和国际竞争力。
附录1
本文采用后验差法对模型拟合精度进行评价,后验差检验的原理如下:
设e(i)为原始数据列z0(i)与拟合数据列z1(i)的残差,即e(i)=z0(i)-z1(i)。
(7)
式中z1为原始序列均方差,z2为残差序列均方差。
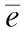
(8)
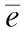
通过后验差比值c和小误差概率p,判断模型的预测精度,c和p值获取源于邓聚龙的《灰色预测与决策》。预测精度等级如下表6所示。
附录2
系统状态即风险值划分方法主要有样本方差、相对误差和聚类,方差和相对误差划分港口投资风险状态与实际状态相差较大,聚类分析既能将相似性较高样本聚集又能克服与实际状态相差较大的弊端,聚类分析划分风险状态标准比样本差划分风险状态标准更加合理。因此本文采用聚类分析方法划分港口风险分级状态。
聚类分析是把研究对象按照性质相似聚为一类,性质差异较大聚在不同的类,建立在样本“距离”基础上的表示方法。因此投资风险值“距离”较近的聚为一类,风险值“距离”较远的聚在不同类。K-均值聚类适用于对港口历年的投资风险数据进行有效的聚类,合理划分出风险值的状态等级。
[1] Frankel E G. Port or shipping project appraisal under risk[J]. Maritime Policy &Management, 1989, 16(3): 213-221.
[2] van Ham H, KoppenjanJ. Building public-private partnerships: Assessing and ma-naging risks in port development[J]. PublicManagement Review, 2001, 3(4): 593-616.
[3] Lam J S L, Su S. Disruption risks and mitigation strategies: An analysis of Asian ports[J]. Maritime Policy& Management, 2015, 42(5): 415-435.
[4] Asteris M, Collins A. UK container port investment and competition: Impediments to the market[J]. Transport Reviews, 2010,30(2): 163-178.
[5] Koh Y K. Optimal investment priority in container port development[J]. Maritime Policy & Management, 2001, 28(2): 109-123.
[6] Rodrigue J P, Notteboom T, Pallis A. The financialization of the port and terminal industry: Revisitingrisk and embeddeness[J].Maritime Policy & Management,2011,38(2):191-213.
[7] Simkins Z S, Stewart R D.Factoring a real value of cargo in port investment a-nd funding decisions[J]. Maritime Policy &Management, 2015, 42(7): 712-728.
[8] Chen M. The use of the interest rate spread for forecasting business cycle turning points and asset allocation: A Markov switch approach[R]. Working Paper, 2000.
[9] 王春峰, 万海辉, 李刚. 基于MCMC的金融市场风险VaR的估计[J]. 管理科学学报,2000, 3(2): 54-61.
[10] Siu T K, Ching W K, Fung S E, et al. On a multivariate Markov chain model for credit risk measurement[J]. Quantitative Finance, 2005, 5(6): 543-556.
[11] 高金余, 陈翔. 马尔可夫切换模型及其在中国股市中的应用[J]. 中国管理科学, 2007, 15(6): 20-25.
[12] 杨继平, 张春会. 基于马尔可夫状态转换模型的沪深股市波动率的估计[J]. 中国管理科学, 2013, 21(2): 42-48.
[13] 陈守东, 王妍. 我国金融机构的系统性金融风险评估—基于极端分位数回归技术的风险度量[J]. 中国管理科学, 2014, 22(7):10-17.
[14] Liang Xue, Dong Yinghui. A Markov chain copula model for credit default swa-ps with bilateral counterparty risk[J]. Communications in Statistics Theory and Meth-ods, 2014,43(3): 498-514.
[15] 黄杰. 沿海港口吞吐量与国民经济关系研究[D]. 大连:大连海事大学博士论文, 2011.
[16] 钟铭, 吴艳云, 栾维新. 港口物流与城市经济协同度模型[J]. 大连海事大学学报, 2011, 37(1): 80-82.
[17] 王洪青, 祁春节, 刘欢. 港口对腹地经济贡献弹性的U型曲线及其理论解释[J].地域研究与开发, 2013, 32(2): 22-26.
[18] 李电生, 员丽芬. 港口群物流系统效率评价[J]. 北京交通大学学报, 2010, 9(2): 42-47.
[19] 张小蒂, 邓娟. 中国港口效率测度及提升研究[J]. 浙江大学学报(人文社会科学版), 2013, 43(4): 39-51.
[20] 汪传旭, 崔建新. 长江三角洲港口群物流系统动力学分析模型[J]. 交通运输工程学报,2007, 7(5): 77-83.
[21] 丁国蕾,刘云啸,王晓光. 长江三角洲主要港口间的协调发展机制[J]. 城市发展研究,2016, 23(3): 64-71.
[22] 隋聪, 谭照林, 王宗尧. 基于网络视角的银行业系统性风险度量方法[J]. 中国管理科学, 2016, 24(5):54-64.
[23] 张晨, 杨玉, 张涛. 基于Copula模型的商业银行碳金融市场风险整合度量[J].中国管理科学, 2015, 23(4): 61-69.
[24] 吴建华, 王新军. 内生性回收率与信用风险违约度量研究[J].中国管理科学, 2016, 24(1): 1-10.
[25] Ramchand L, Susmel R. Variance and covariances of international stock returns: The international capital asset pricing model revisited[J]. Journal of International Financial Markets, 1998, 8(1): 39-57.
[26] 罗平, 姜仁荣, 李红旮, 等. 基于空间Logistic和Markov模型集成的区域土地利用演化方法研究[J]. 中国土地科学, 2010, 24(1): 31-36.
[27] 张桦, 魏本刚, 李可军, 等. 基于变压器马尔可夫状态评估模型和熵权模糊评价法的风险评估技术研究[J]. 电力系统保护与控制, 2016, 44(5): 134-140.
