栈式降噪自编码器的标签协同过滤推荐算法

霍 欢,郑德原,高丽萍,杨沪沪,刘 亮,张 薇

1(上海理工大学 光电信息与计算机工程学院,上海 200093) 2(复旦大学 上海市数据科学重点实验室,上海 201203)

1 引 言

协同过滤算法通过矩阵分解技术挖掘出用户和推荐对象的隐含特征,帮助用户在海量过载的互联网信息中获取对自己有用的信息,是近年来推荐系统研究的热点.但协同过滤算法对于稀疏的评分矩阵没有很好的解决方案.目前有不少较新的协同推荐技术都在这方面做了努力,如[1]考虑到了推荐对象的标签特征,[2]引入了混合推荐技术等,这在一定程度上能缓解评分矩阵稀疏的问题,但同时标签矩阵大多同样是非常稀疏的,所以仅仅依靠引入原生标签信息不足以克服协同过滤算法的缺点.

推荐系统的另一个方法是基于内容的推荐.[3]通过用户或推荐对象的肖像刻画,维护一个特征向量或属性集来构建推荐系统.基于内容的推荐缺点在于不能自动抽取深层特征,无法挖掘出对象的深层隐式特征和用户的潜在兴趣,再加上业界对互联网隐私问题的考虑,导致这种问题更加严重.所以基于内容的推荐需要和协同过滤配合,构建混合推荐系统以产生更好的推荐效果.

如何增加推荐数据的信息量和挖掘内容信息深层特征,是提升推荐算法性能表现的关键.基于内容推荐的算法在抽取特征时,通常会采用LDA(Latent Dirichlet Allocation)[4]等模型,此类模型在传统基于内容的推荐中有着不错的表现.另一方面,深度学习具有自动学习深层特征的能力,非常适合与协同过滤算法配合,应用于基于内容信息的推荐模型上.本文提出基于深度学习的DLCF(Deep Learning for Collaborative Filtering)算法,首先利用栈式降噪自编码器SDAE(Stacked Denoising Auto Encoders)[5]训练出推荐对象和其标签的特征向量,得出新的标签物品矩阵,将信息量较少稀疏标签矩阵转化为具有深层特征信息的标签矩阵,大幅度增加了原始数据的信息量,然后再和原始评分矩阵结合进行协同过滤处理.

本文的贡献主要包括以下三个方面:

1)将深度学习算法应用于基于内容的推荐模型上,通过抽取深层特征,大幅提升了原始数据的信息量;

2)通过构建辅助矩阵,将先前训练得到的物品和标签特征向量与原始评分矩阵结合,最大限度发挥了数据标签的作用,将数据标签、内容信息与评分矩阵统一到算法框架中去;

3)在真实数据上对算法性能进行了实验,通过多种评估方法分在横向和纵向上对比了不同算法的表现,并且指出了模型参数对算法性能的影响.

文章第2节介绍了背景知识,第3节阐述了DLCF算法的具体细节,第4节在真实数据集上进行了实验验证.

2 背景知识

目前的协同推荐技术主要结合协同过滤模型和基于内容模型进行尝试[6,7].对于辅助信息的使用,[8]提出物品标签可以应用于协同过滤算法中,[9]通过项目类型信息来降低矩阵的稀疏性和冷启动问题,[10]通过分析标签系统中的对象的关系提出了社会化标签推荐方法,[11]提出了一种基于标签的系统同推荐方法Tag-CF.但这些方法只能利用数据已经提供的辅助信息,无法挖掘出数据隐含的深层信息,效果并不理想.

由于深度学习具备充分挖掘数据隐含信息的能力,文献[12] 使用DBN(Deep Belief Networks)来挖掘深层内容信息,[13]提出一种基于关系的Relational SDAE算法.但这些算法仅仅应用了深度学习的特征,而没有将其与协同过滤算法有机结合起来.

将深度学习模型应用于基于内容的推荐中,并将其与协同过滤算法相结合,是本文提出的DLCF算法核心.本文采用的深度学习模型SDAE是将多个DAE(Denoising Auto Encoder)[14]堆叠起来形成的一种模型,能抽取内容信息的深层特征,同时拥有较强的可解释性和较低的模型复杂度.SDAE能从原始内容信息中抽取新的特征维度,训练出标签内容矩阵,大大增加了原始数据的可用信息量,再将新的内容标签矩阵融入到概率矩阵分解模型PMF(Probabilistic Matrix Factorization)中,使得基于内容的推荐模型和协同过滤完美结合在一起.同时,本文采用SGD(Stochastic Gradient Descent-随机梯度下降) 通过最小化损失函数来训练模型参数,克服了深度学习算法迭代速度慢的问题,完美解决了传统协同过滤算法中矩阵稀疏的问题和基于内容推荐算中存可用内容信息不足的缺点.

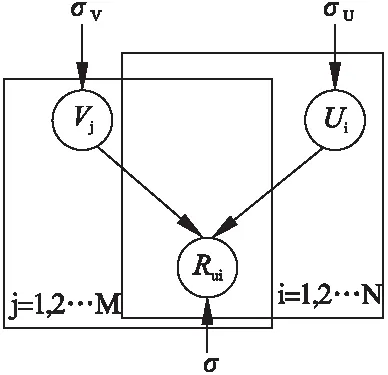
图1 概率矩阵分解Fig.1 Probabilistic matrix factorization

2.1 概率矩阵分解

概率矩阵分解模型(PMF)将先验概率分布引入到传统矩阵分解模型中,假设观测到的评分数据的条件概率:

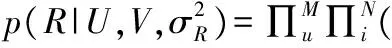
(1)

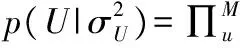
(2)

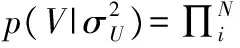
(3)

模型原理如图1所示.

2.2 栈式自编码器

DAE即降噪自编码器,模型由编码器和解码器构成,每一个编码器都对应有一个解码器,通过编码和解码的过程处理数据噪声.图2展示了栈式降噪自编码器SDAE是将多个DAE堆叠起来的前馈神经网络,类似于多层感知机,每一层是下一层的输入,也是上一层的输出.SDAE即栈式降噪自编码器使用逐层贪婪训练策略依次训练网络的每一层,进而预训练整个深度网络,其思想就是将多个DAE堆叠在一起形成一个深度的框架,模型通过受损残缺的输入和已修复的输出来训练中间模型通过受损残缺的输入和已修复的输出来训练中间层.

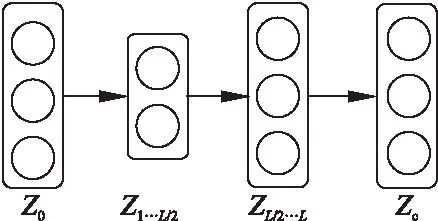
图2 栈式降噪自编码器Fig.2 Stack denoising auto encoder

图3展示了SDAE模型的具体结构,公式(4)为SDAE的训练模型.其中Zc是被若干标签标记的向量组成的矩阵,作为SDAE最后的输出;Z0表示模型中最初受损的输入矩阵;ZL是模型的中间层,最终需要训练得出的目标矩阵为ZL/2,表示经Z0和Zc训练得出含有深层内容信息的矩阵.Wl和bl分别表示SDAE模型第l层的权重矩阵和偏置向量,λ表示正则参数,‖·‖F是Frobenius范数.

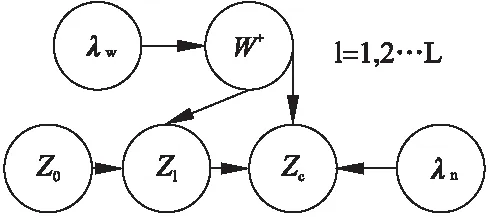
图3 栈式降噪自编码器训练模型Fig.3 Stack denoising auto encoder training model

(4)

3 CF算法

3.1 训练标签内容矩阵

根据SDAE模型和原理,输出矩阵Zc和受损输入矩阵Z0都是已观测变量,对Zc做如下定义:对于SDAE的每一层l:

Wl,*n～

(5)

bl～

(6)

其中Wl,*n表示第l层权重矩阵中第n列,Ik表示单位矩阵的第K个对角值.对于Zc和ZL:

Zl,j*～

(7)

Zc,j*～

(8)

其中σ(·)表示sigmoid函数,λw,λn和λs均为模型参数.基于以上定义,最大化Wl,bl,Zl,Zc的最大后验概率,等同于最小化上述变量的联合对数似然函数,定义模型损失函数为:

(9)

定义Ti,j为一个二值量,当物品j包含标签i的时候,Ti,j为1,否则为0.则由ZL/2,j*和原始标签矩阵Ti,j,求出标签和物品的隐因子向量ti和vj:

(10)

其中λt和λv为正则参数,ci,j在物品j包含标签i的时候设为1,否则设为一个很小的值,譬如0.001或0均可.

3.2 构建用户标签矩阵

由标签和物品的特征向量ti和vj,可以构建DLCF算法中的标签物品矩阵G.Ru,i表示用户u对物品i的评分,Gi,t表示物品i对标签t的取值,包含标签t则取值为1,否则为0.通过联合矩阵R和G,得到目标矩阵H:

(11)

3.3 构建DLCF算法

在构造出用户-标签矩阵H后,分别利用原来的评分矩阵R和新构造的用户-标签矩阵对H对传统协同过滤算法进行改进.如图4所示,U和V分别表示用户和物品包含的隐式特征向量,Q表示标签和用户隐式特征的关系,U将作为R和H之间信息流通的桥梁:

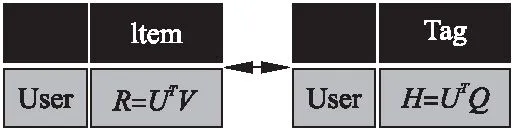
图4 构建联合矩阵Fig.4 Co-association matrix construction

将矩阵H融入到PMF中,构造出新的损失函数:

(12)

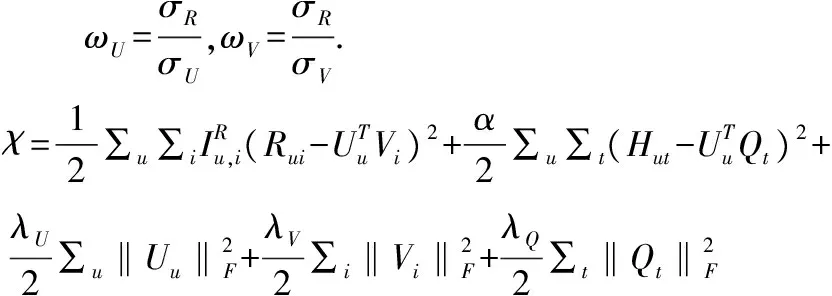
(13)

其中λU=ωU+φU,λV=ωV,λQ=ωQ.

图5展示了DLCF的框架,与传统的PMF模型相比,DLCF使用了由SDAE拓展出的用户-标签矩阵H,将其与原始评分矩阵Ru,i结合,丰富了原始数据的信息量,将基于内容挖掘出的隐含信息应用在了协同过滤算法中.

3.4 SGD训练算法

SGD(Stochastic Gradient Descent-随机梯度下降)算法也叫增量梯度下降法,是在传统梯度下降法的基础上改进而来,收敛速度快很多,是常用的参数训练算法.SGD通过最小化损失函数来训练模型参数,根据每个样本来迭代更新一次,可以控制下降速率和迭代次数,使得参数的训练更可控.本文使用SDG来训练χ.

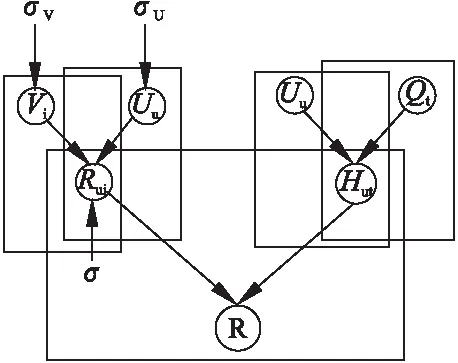
图5 作为辅助信息的联合矩阵Fig.5 Co-association auxiliary matrix

Algorithm1：DLCF⁃SGDtrainingalgorithmInput：评分矩阵R，特征向量维度K，学习率η，比例参数α，正则参数λUλVλQOutput：U，V1． 初始化：用一个较小的值随机构造U，V和Q2． while(erroronvalidationsetdecrease)3． ΔUχ=I(UTV-R)V+α(UTQ-H)Q+λUUΔVχ=[I(UTV-R)]TU+λVVΔQχ=α(UTQ-H)TU+λQQ4． setη=0．15． while(χ(U-ηΔUχ，V-ηΔVχ，Q-ηΔQχ)>χ(U，V，Q))6． setη=η/27． Endwhile8． U=U-ηΔUχ V=V-ηΔVχQ=Q-ηΔQχ9． Endwhile10． ReturnU，V

4 实验结果与分析

4.1 实验数据集

实验数据集采用国内知名社交分享网站豆瓣读书(https://book.douban.com/)中的数据.每本书都有用户从1到5的评分,并且每本书都有用户标注的特征,可以用于基于内容模型中的特征向量使用,很适合DLCF算法的使用场景.数据集包括89434本书,373241名用户,以及12436087条评分数据.实验选取不同稀疏程度的数据集,对于不同稀疏程度的数据集,分别选取80%作为训练数据,20%作为测试数据,并且在实验的过程中将数据随机分成5分,进行交叉检验数据格式如表1所示.

表1 数据格式
Table 1 Data format

UserIDBookIDRatingLabels用户编号图书编号评分标签

4.2 算法评估标准

推荐系统的评估方式一般有两种,一种评估预测评分与用户实际评分的贴近程度,这种评估方式很常见,本文采用均方根误差(Root Mean Square Error,简称RMSE)来作为算法性能衡量的标准.

(14)

其中τ表示用户u对物品i评分存在的集合.

另一种评估反映算法预测的准确程度.我们采用recall@R作为度量方式.recall@R通过选取测试用户,将推荐结果排序并选取其中最受用户喜欢的R个,得出其与用户所有标记总数的比值,值越大表明算法预测效果越好.

(15)

4.3 对比模型和实验设置

为了体现出DLCF算法的特点,我们选取三种算法作为基准测试,传统的协同过滤,这里选取概率矩阵分解(PMF)、结合标签信息的协同过滤算法(Tag-CF)和未使用标签的深度学习算法(DBN).首先利用上述的三个算法和DLCF做横向对比,然后再观测DLCF在不同实验设置下的纵向对比表现,以此综合评判各算法的性能表现.

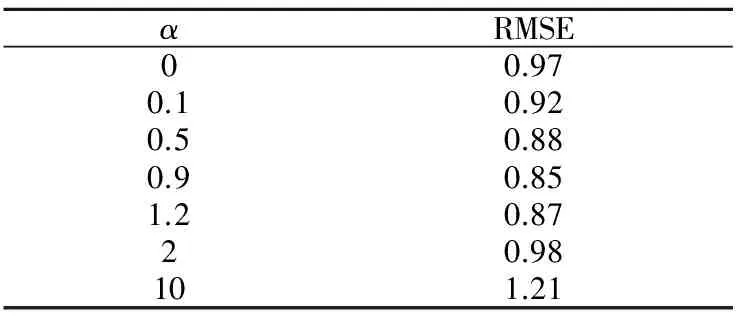
在更进一步的实验对比之前,先考察公式(12)中的参数α,即用户-标签矩阵在整个模型中的影响因子.若将α置为0,则表示不考虑用户-标签矩阵,此时算法退化为不考虑标签的传统协同过滤算法.在本文所进行的实验中,其它参数固定时,α=0.9时能够最小化RMSE,如表2所示.

表2 参数α对模型的影响
Table 2 Parameterαwith RMSE

αRMSE00．970．10．920．50．880．90．851．20．8720．98101．21

对于其它参数λU=ωU+φU,λV=ωV,λQ=ωQ,ωU=σR/σU,ωV=σR/σV,表示模型中的正则参数λU,λV,λQ是由其它隐含参数复合而成的,理论上我们需要对每个隐含参数取值,然后再计算λU,λV,λQ的值.但在实际使用中,可以先对λU,λV,λQ设置一个比较小的值,例如λU=λV=λQ=0.001,然后通过实验中交叉验证进行调节,结果证实,这样做对算法性能影响并不明显.

表3 不同稀疏程度的数据
Table 3 Dataset sparsity

dataset⁃adataset⁃b98．78%90．54%

接下来的对比实验中,将实验数据按照稀疏程度分成如表3所示的两份,然后分别针对两种评估方式对各个算法进行性能比较.

4.4 算法横向比较

横向对比部分侧重在比较不同算法相同场景下的表现.对于recall@R这种评估标准,我们比较不同R值下各算法的表现.对于RMSE标准,通过选择不同的特征向量分解维度K的值,来对比各种算法的表现.上述比较会在不同稀疏度的数据集上分别实验.

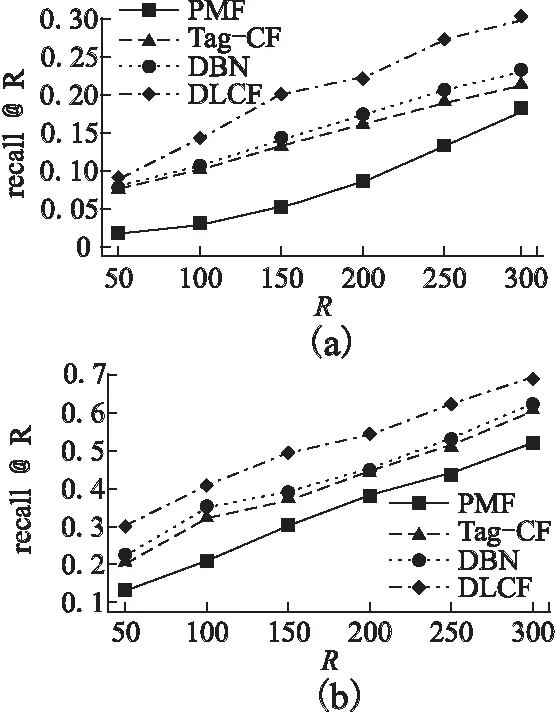
图6 数据集a,b下recall@R的表现Fig.6 Recall@R on dataset a and b

首先观察四种算法在recall@R上的表现,如图6所示，会发现传统不引入辅助信息的协同过滤算法表现最差,DBN和Tag-CF由于都只采用了部分辅助信息,性能差异表现并不大,而DLCF显著优于其他三类算法.同时很明显可以看出,算法在较稠密数据集上的表现要好于稀疏数据的表现.

接下来针对RMSE观察,会发现情况基本和recall@R类似,DLCF仍然表现出很大的优势.如图7所示，同样,算法在稀疏数据集上的表现差于在稠密数据集上的表现.并且可以观察到,在稠密数据集上,DBN和Tag-CF表现的差异没有其在稀疏数据集上的差异那么大.这是因为稠密数据集信息量较大,一定程度上弥补了算法性能的差异.综合上述横向比较可以看出,算法性能表现的关键在于是否能够尽可能的利用已有数据的隐含信息.

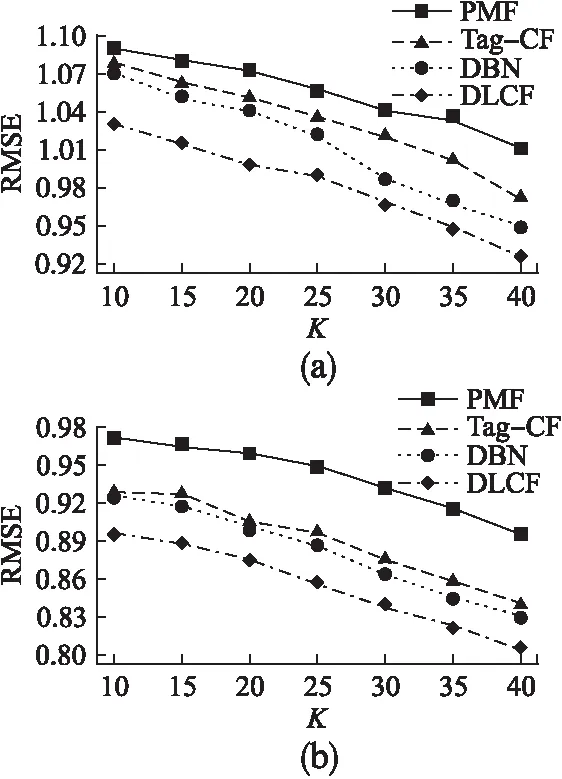
图7 数据集a,b下RMSE的表现Fig.7 RMSE on dataset a and b

4.5 算法纵向比较

横向对比部分侧重在于比较不同算法相同场景下的表现,而纵向比较主要探索参数对于DLCF的影响.经过多次实验发现,纵向对比中以recall@R为评估标准的实验表现比RMSE差异更明显,所以此部分着重展现以recall@R为评估标准的实验结果.结合深度学习和协同过滤模型的特性,并且经反复实验之后,本文分别选取SDAE模型的中间层L/2和模型参数λn作为关键参数.

首先针对参数λn进行实验,实验结果如图8所示.λn在SDAE中用来训练中间层,是生成DLCF新标签矩阵的关键参数.观察实验结果会发现,λn的值并不是越大越好或者越小越好,而是存在一个表现良好的范围.当λn值很小时(通常小于1),算法性能表现很差,这时提高λn的值,会提升算法性能表现.但当λn的值在三位数以后,再继续提升λn,算法性能提升已经不明显.而且同样,模型在较稠密数据集的表现显著好于在稀疏数据集上的表现.

图8 DLCF中λn对recall@R的影响Fig.8 Recall@R under different λn on DLCF

最后来看以SDAE的中间层L/2为观测变量的实验结果,如图9所示.显而易见的是,较稠密数据集上的算法表现明显好于稀疏数据集.对于中间层,当L/2=1时,由于层数太少,性能表现差于L/2=2和L/2=3时的结果.但对于L/2=2和L/2=3时的结果,会发现性能差异很小,而且随着R值的变化,双方结果互有胜负.考虑到深度学习模型中,中间层每增加一层,算法复杂度就会提升,并且在调参方面也更加困难,所以在保障算法性能的前提下,不建议增加太多的中间层.

图9 DLCF中L/2对recall@R的影响Fig.9 Recall@R under different L/2 on DLCF

5 结 论

传统协同过滤算法无法克服矩阵稀疏的问题,即使引入标签信息,标签矩阵也同样存在着矩阵稀疏问题,无法拥有理想的性能表现.而传统基于内容的推荐算法由于自身的特性,不适合与协同过滤算法直接融合.本文利用深度学习模型挖掘数据隐含信息的特性,通过处理原始的物品标签信息,大幅度提升了原始数据的可用信息量,将基于内容的推荐模型和协同过滤模型结合在一起,提出了DLCF算法.在真实数据集上的实验表明,DLCF算法能够取得优于传统推荐模型的性能.

另一方面,引入深度学习模型能够提升算法性能,但对于算法的调参无疑提出了更高的要求,并且算法的复杂度也相比传统算法提升不少.未来的工作将为集中解决上述问题,提升算法的可解释性和工程意义.

[1] Li W J,Yeung D Y,Zhang Z.Generalized latent factor models for social network analysis[C].Proceedings of the 22nd International Joint Conference on Artificial Intelligence (IJCAI),Barcelona,Spain,2011:1705-1710.

[2] Grivolla J,Badia T,Campo D,et al.A hybrid recommender combining user,item and interaction data[C].Proceedings of the International Conference on Computational Science and Computational Intelligence (CSCI),Las Vegas,Nevada,USA,2014,1:297-301.

[3] Shen Y,Fan J.Leveraging loosely-tagged images and inter-object correlations for tag recommendation[C].Proceedings of the 18th ACM International Conference on Multimedia (ACMMM),Firenze,Italy,2010:5-14.

[4] Blei D M,Ng A Y,Jordan M I.Latent dirichlet allocation[J].Journal of Machine Learning Research,2003,3:993-1022.

[5] Vincent P,Larochelle H,Lajoie I,et al.Stacked denoising autoencoders:learning useful representations in a deep network with a local denoising criterion[J].Journal of Machine Learning Research,2010,11:3371-3408.

[6] Zheng D Y,Huo H,Chen S Y,et al.LTMF:Local-based tag integration model for recommendation [C].Proceedings of the 11th EAI International Conference on Collaborative Computing,Wuhan,China,2015,11:296-302.

[7] Van den Oord A,Dieleman S,Schrauwen B.Deep content-based music recommendation[C].Advances in Neural Information Processing Systems,Harrahs and Harveys,Lake Tahoe,2013:2643-2651.

[8] Vig J,Sen S,Riedl J.The tag genome:encoding community knowledge to support novel interaction[J].ACM Transactions on Interactive Intelligent Systems (TiiS),2012,2(3):13:1-13:44.

[9] Pirasteh P,Jung J J,Hwang D.Item-based collaborative filtering with attribute correlation:a case study on movie recommendation[M].Intelligent Information and Database Systems,Springer International Publishing,2014:245-252.

[10] Bobadilla J,Ortega F,Hernando A,et al.Recommender systems survey[J].Knowledge-Based Systems,2013,46(1):109-132.

[11] Kim B S,Kim H,Lee J,et al.Improving a recommender system by collective matrix factorization with tag information[C].2014 Joint 7th International Conference on Soft Computing and Intelligent Systems (SCIS) and 15th International Symposium on Advanced Intelligent Systems (ISIS),Kita-Kyushu,Japan,2014:980-984.

[12] Wang X,Wang Y.Improving content-based and hybrid music recommendation using deep learning[C].Proceedings of the ACM International Conference on Multimedia,Orlando,Florida,USA,2014:627-636.

[13] Wang H,Shi X,Yeung D Y.Relational stacked denoising autoencoder for tag recommendation[C].Proceedings of the 29th AAAI Conference on Artificial Intelligence,Austin,Texas,USA,2015:3052-3058.

[14] Vincent P,Larochelle H,Bengio Y,et al.Extracting and composing robust features with denoising auto encoders[C].Proceedings of the 25th International Conference on Machine Learning,Helsinki,Finland,2008:1096-1103.