链路预测中的一种局部结构相似度算法

尹永超，徐 敏，傅皇麟，孙胜男

1(南京航空航天大学 计算机科学与技术学院，南京 211106) 2(软件新技术与产业化协同创新中心，南京 210023) 3(云南师范大学 外国语学院，昆明 650500)

1 引 言

21世纪是复杂的世纪，随着计算机技术的迅猛发展以及人们对现实世界的认识越来越深入，复杂网络作为一种研究复杂化的网络结构及其演化技术，越来越受到人们的重视.通过抽象化的网络结构去模拟现实世界中人与人、人与物之间的相互关系，从而推动现实世界中各种理论及应用的不断完善与进步.而链路预测[1]作为复杂网络的一个重要应用，通过网络中节点的结构以及属性等信息建立网络关系模型，然后结合复杂网络的特性去预测还未产生连接的两个节点之间产生连接的可能性.最后结合具体的应用对相似的节点进行推荐或加权，从而对提升网络传播效率，增加节点之间的互动以及进一步了解复杂网络的传播机制具有重要意义.例如我们通过对社交网络中各好友之间关系的分析来预测尚未建立连接的两个人之间进行交互的可能性，从而对其进行好友推荐[2].或者音乐、电影、新闻类的娱乐网站，通过用户行为分析，预测不同用户的喜好以及相互之间的爱好相似度，然后给不同用户推荐其可能感兴趣的物品，这样对提高网站流量增加用户依赖度具有很大作用.

当前的链路预测算法大都基于相似度指标，即两个节点之间的相似度越大则节点之间连接的可能性就越大.而大多基于节点相似度指标的算法都以共同邻居为依据，即两个节点之间共同邻居数量越多那么这两个节点之间就越相似[3].如CN、Salton、Jaccard、HPI、HDI、AA、RA等，这些指标都是在共同邻居的基础上进行改进，以适应不同的网络结构.一些较为复杂的方法，不仅考虑节点的属性信息，同时利用马尔科夫链[5]及机器学习算法，如随机游走的相似性指标[4]、朴素贝叶斯[6]、神经网络[7]、支持向量机、k近邻等有监督的分类方法.这些方法往往具有较高的预测准确度，但由于计算复杂较高通常仅适用于小规模的网络.针对不同网络结构模型的研究也慢慢受到各学者的重视，对于一些比较规律的网络我们可以针对特殊的网络结构进行预测.如基于层次结构模型[8]的算法，这种算法认为网络中的节点可以被聚类成若干群组，而每个群组中的节点又可以被聚类为下一级节点.这种类似于族谱树的结构，可以很好的模仿新陈代谢以及大脑神经网络，从而达到较好的预测效果.另一些应用较为广泛的链路预测算法则将网络中的一些影响因素以有向或者加权的形式进行组合，从而进一步区分不同关系下的预测效果，以达到提高预测精度的目的.近年来基于二部分网络的链路预测算法得到广泛应用[9]，其在电子商务网络、在线娱乐、新陈代谢网络中的应用都取得了很好的预测效果.目前对社交网络的链路预测，逐渐从依赖于节点的属性信息向只利用网络结构信息转移，而基于结构信息的有向加权网络[10]也越来越受到更多学者的重视.

本文首先介绍了一些较常用的基于节点相似度的指标算法，然后对真实数据集中的网络结构进行提取，选取了几个比较常见的基本网络模型，对以上各指标在不同网络模型中的侧重点进行分析.通过比较各算法的优劣，我们提出了一个较为新颖的基于邻居节点结构相似度的LSCN指标算法.通过比较一个节点A与另一个节点B的所有邻居节点的结构相似度来判断节点A与节点B之间连接的可能性.并且由表2我们可以看出，算法的预测效果在个别网络中有很大提升.之后我们通过进一步考虑二阶邻居节点的结构相似度，又提出了一个改进的LSCN-Ⅱ指标算法，并通过实验选取其最佳的α参数，使得不同网络中的最终的预测效果与LSCN指标相比得到进一步提升.

2 基于局部信息的相似度指标

相似度指标指的是节点之间的相似程度，相似度指标越大就指两个节点之间越相似且越有可能产生连接.目前大多数的相似度指标算法大都依赖于共同邻居，即两个节点之间的共同邻居数量越多那么这两个节点越相似.

2.1 仅考虑共同邻居数量的CN指标

CN指标即Common Neighbors，是基于局部信息的最简单的相似性指标，如果两个节点之间的共同邻居数量越多那么这两个节点就越相似.CN指标的定义是：对于网络结构中的节点Vx，其邻居节点的集合为Γ(x)，则连接节点Vx和Vy的相似度就是它们的共同邻居数，即

Sxy=|Γ(x)∩Γ(y)|

(1)

2.2 考虑共同邻居节点数量及终节点度数的指标

CN指标虽然具有比较低的算法复杂度，且具有较高的预测效果.但是仅仅考虑到了节点间共同邻居的数量，而忽略了节点自身的影响.根据弱连接效应，并且考虑终节点自身的影响，以不同的形式又产生了以下不同的相似性指标：

Salton指标

(2)

LHN-I指标

(3)

以上公式中kx表示节点vx的度数，Γ(x)表示节点vx相连的邻居节点集合.Salton[11]和LHN-I[12]指标都认为节点vx和vy之间的相似度与两个节点度数的乘积成反比.

Sorenson指标

(4)

Sorenson[13]指标认为节点vx和节点vy之间的相似度与终节点度数之和成反比.

HPI指标

(5)

HPI[14]指标认为节点vx和节点vy的相似度与两个节点中最小的节点度数成反比，通常用来对新陈代谢网络中反应物的拓扑相似程度进行刻画.

HDI指标

(6)

HDI[15]指标与HPI指标相对应，其将节点vx和节点vy之间的相似度定义为两个节点中度数最大的节点倒数.

2.3 考虑弱连接效应的指标

计算节点间的相似度，如果仅仅考虑节点之间共同邻居的数量，未免太过简单.因为对于每个不同的共同邻居节点来说，不同邻居节点的度数也发挥着至关重要的作用.与以上其他节点相比，AA、RA指标不但考虑到了每个不同共有邻居节点度数的影响，同时其将不同的邻居节点度数起到的作用进行累加.其同样考虑到了共有邻居节点的数量，因此在许多网络中，这两个指标通常能起到更好的预测效果.

AA指标

(7)

AA[16]指标将不同共有邻居节点的权重定义为该节点的度数的对数的倒数.并且将节点vx和vy之间的相似度定义为所有不同共有邻居节点的权重之和.

RA指标

(8)

RA[15]指标与AA指标之间的最大区别是其对共同邻居节点权重定义方式不同，前者认为权重以1/k的形式递减，后者则定义为1/logk的形式.

2.4 仅考虑终节点度数的PA指标

Sxy=kxky

(9)

PA[17]指标仅仅考虑终节点自身度数的影响，且终节点度数越高那么这两个节点之间的连接概率就越大.在一些特定的网络中取得了很好的预测效果.如下页表2所示在Router网络中，PA指标的预测效果明显好于其他算法.

2.5 基于局部路径相似性的LP指标

基于共同邻居的相似性指标往往计算复杂度较低，但是由于使用的信息非常有限，并且最终的计算结果区分度不大使得预测的精度很难有所提高.LP[18]指标则是在共同邻居的基础上，进一步考虑三阶路径的影响.虽然计算复杂较高，但是最终的预测效果几乎都有所提升.

Sxy=A2+αA3

(10)

上式中A表示节点的邻接矩阵，A2表示二阶路径的CN指标A3则表示三阶路径矩阵.

3 分析不同网络结构特征

通过对第四章试验中提到的8个真实网络数据集进行筛选，对节点以及边进行组合用python语言进行处理，然后将各真实网络以二维图的形式展示出来.通过对网络结构图的观察，从中提取出了几个比较典型的网络模型.然后对以上各指标在各网络模型中的表现分别进行分析，从而分析各算法的侧重点以及优劣.

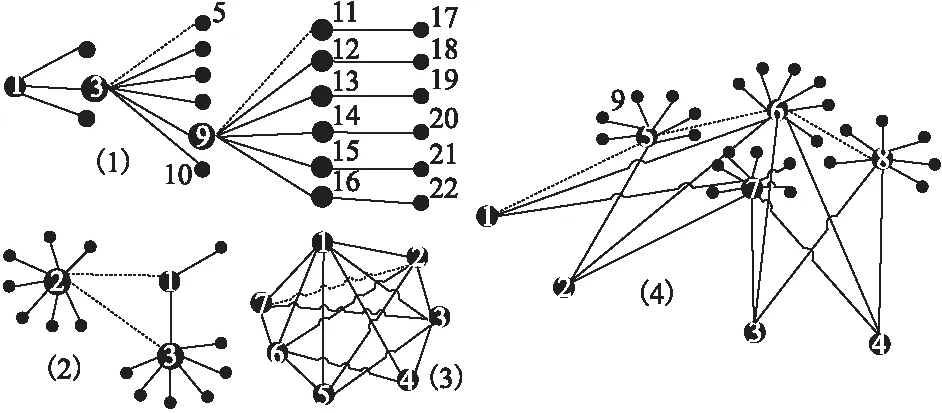
图1 真实数据集得到的几种基本网络模型Fig.1 Several basic network models from real data sets

如图1所示一共选取了四个比较典型的局部网络结构模型，其中实线表示节点之间已经存在的关系，虚线表示各结构中比较常见的预测案例.我们主要分析各算法对虚线连边的预测准确性.对于一些不规则的网络结构，我们发现以上算法都未能达到一个较好的预测效果.如第四章中Power数据集代表的美国西部电力网络，各节点之间没有很规律的网络结构.节点之间的连接可能跟人口数量或者地理位置相关，很难在单一的网络结构中反映出来.

公式(1)-公式(8)提到的各相似度算法主要以邻居节点数量为依据，即邻居节点越多那么这两个节点越相似其连接的可能性就越大.并考虑复杂网络的弱连接效应，邻居节点中度数大的节点对相似度的贡献小于度数小的节点.以图1(2)为例，节点3，5以及节点9，11之间由于没有共同邻居节点，因此以上各公式得出的连接概率都为零.而对于图1(2)中节点2和3由于拥有较高的邻居节点数量，导致其连接概率远远小于1，3，；1，2节点对的计算结果.对于图1(4)中1，5节点对之间由于也没有共同邻居，因此其计算结果也为零.因此对于以共同邻居为依据的算法来说，其预测效果主要依赖于网络中模型(3)所占的比例，即节点的聚类系数比较高时，其预测效果较好.如表2所示在NS网络中各公式都有较好的预测效果，而在NS网络中大部分的局部网络模型也都与图1(3)类似.对于以(1)(2)(4)占比较高的Router网络，各算法的预测效果都比较低.同时我们可以看到PA算法在Router网络的预测效果要明显好于其他网络，通过对其网络结构的分析我们可以看到其大多数的网络模型为(1)(4).也即在Router网络中，一个节点更倾向于连接度数大的节点，与节点之间的共同邻居数量无关.

4 本文提出的新指标算法

由第二章中基本网络模型的分析，我们可以发现对于基于共同邻居数量的各相似度指标算法比较适用于图1中(3)结构模型占比较多的网络.即网络的聚类系数越高，那么使用基于共同邻居数量的相似度指标算法得到的预测效果越好.但是对于像Router、C.elegans那样的包含图1中(1)(2)(4)模型较多的网络，很难达到一个较好的预测效果.针对以上特点以及文章[19]中提到的局部差异度，我们想到了一个基于邻居节点结构相似度的LSCN指标算法，并且由实验结果得出其在各个网络中都能达到一个更好的预测效果.

4.1 LSCN指标

LSCN(Local Structure-Common neighbors)指标的思想即为：一个节点与另一个节点的连接概率，等比于此节点与另一个节点的所有邻居节点的结构相似度.其中结构相似度可以定义为：

(11)

上式中Γ(x)表示节点x的邻居节点集合；D(x)表示节点x的度数即邻居节点数量；|D(x)-D(y)|+1则表示节点x和节点y之间邻居节点数量的差异，为了避免数量相等结果为零导致计算结果不正确，我们将其绝对值进行加一处理.以上公式即表示两个节点之间，度数越接近差值越少并且共同邻居数量越多，那么这两个节点的结构就越相似.由结构相似度的公式我们将LSCN指标定义为：

(12)

由表2中的实验结果可以看出，与其他相似度指标相比LSCN指标得到的预测效果在多个数据集中都有所提高.

4.2 LSCN-Ⅱ指标

由2.5节中的LP指标启发，我们想到了邻居节点的二阶路径，即对LSCN指标进行扩展进一步考虑邻居节点的下一级邻居的结构相似度.从而提出了LSCN-Ⅱ指标：

(13)

上式中的Sxy即为公式12计算得出的节点x，y之间的LSCN指标.α表示二阶邻居节点结构相似度所占的重要性，当α为0时即表示LSCN指标.

图2 不同网络中AUC预测结果随α变化图Fig.2 AUC predicted results with the change of α in different networks

我们对α分别取0到1之间的不同值，然后通过实验结果观察期最终预测效果，从而选取最佳α值使得不同网络中LSCN-Ⅱ指标可以达到最佳的预测效果.并且由表2可以看到，通过选取最佳的α值与LSCN指标相比，使得预测效果得到进一步提升.并且与其他相似度指标相比，最终其在Power、Router网络中预测效果提升显著.图2为在当α取不同值时在不同网络中根据LSCN-Ⅱ指标计算出的AUC预测结果.

表1 不同网络中的最佳α取值Table 1 Best α value in different networks

表1为LSCN-Ⅱ指标下在不同网络中的最佳α取值，α为0时即表示LSCN指标取得最佳结果：

5 实验及结果

本文所涉及的实验数据都来源于真实网络，读者可以到网站上进行下载*http://www.linkprediction.org/index.php/link/resource/data..其中Power表示美国西部电力网络，节点代表变电站，边则代表连接变电站之间的高压线，共有6594条边和4941个节点；Router表示的是路由器网络，边代表不同路由器之间有连线，共有6258条边和5022个节点；email表示某一电子邮件网络，边代表不同个人之间有邮件往来，共有32709条边和1133个节点；C.elegans表示线虫神经网络，节点代表线虫的神经元突触，边则表示神经元突触之间有链接，共有2148条边和297个节点；Yeast表示某一蛋白质相互作用网络，节点代表的就是蛋白质，边则表示连接的两个蛋白质之间有相互作用关系，共有11855条边和2617个节点；PB表示政治家博客网络，节点代表不同政客的博客地址，边则表示这些网页之间存在相互连接，共有19022条边和1224个节点；USAir表示美国航空交通网络，网络中的不同节点代表不同的机场，边表示机场之间有直飞航线，共2126条边以及332个节点；NS表示科学家之间的相互合作网络，节点代表不同的科学家，边则表示不同的科学家之间存在合作关系，共有8226条边以及1589个节点.

5.1 评价指标

衡量链路预测算法好坏的主要指标有AUC[19]、精确度和排序分，他们分别以不同的方法对各算法的预测效果进行计算.精确度指标首先取出测试集中，依据不同算法计算得到的，分数最靠前的L个连边，然后找出这L个连边实际存在的概率.排序分则是考虑，测试集中正确边的得分在所有排列中的位置.AUC是应用最广泛的一种衡量链路预测结果的方法，它在考虑测试集中所有已存在边的得分顺序同时，同样考虑到了不存在边的得分顺序.根据所有已存在边的得分顺序与不存在边的差距来判断算法的好坏.如果所有已存在边的得分越靠前，并且与不存在边的排列顺序越远，说明算法的预测效果越好.在实际应用中，特别是当样本非常多时，我们可以通过抽样的方法来获取结果的近似值.即每次随机的从测试集中随机的选取一条边，然后再从不存在边集合中随机选取一条边.如果测试集中边的预测分数值大于不存在边的预测分数值则加1，如果相等则加0.5.最终在n次独立的比较后n′就意味着，测试集中存在边的分数值大于不存在的边的分数值的次数，n″表示双方相等的次数.那么预测精度AUC就可以表示为：

表2 不同相似度指标下的AUC预测结果Table 2 AUC results for different similarity indexes

(14)

5.2 实验结果

我们将不同的实验数据集随机分成两部分，其中90%为训练集，10%为测试集.然后在训练集中根据各算法去计算不同节点之间的相似度得到所有节点间的相似度矩阵.然后拿相似度矩阵在测试集计算存在边和不存在边的连接概率，最后根据AUC公式去计算预测准确度.不断重复以上步骤，依据平均结果去比较不同算法的预测效果.

实验结果：

从表2中我们可以看出：与仅考虑邻居数量的CN指标，或者考虑邻节点数量及邻居节点度数的AA、RA指标相比本文提出的LSCN指标算法，在考虑共同邻节节点的基础上通过节点之间的邻居节点结构相似度，其得出的预测效果在多个真实网络中都有不同程度的提高.并且通过进一步考虑二阶邻节点结构相似度我们可以看出在Power网络中的预测效果明显提升不少，并且通过选取最佳的α值使得算法的预测效果在不同网络中进一步有所提升.

6 总结与展望

仅考虑邻居节点数量及度数的指标在计算相似性的链路预测中虽然不能起到最好的预测效果，但是由于其计算复杂度低计算所需要的资源较少，因此在许多方面都得到了应用.本文选取8个真实的网络数据集然后对其进行网络化，从中提取出了4个比较典型的基本网络模型数据.然后对各相似度算法在不同网络模型中的表现进行分析，比较各相似度算法在不同网络模型下的预测效果.然后在共同邻居的基础上提出了一个新的基于邻居节点相似度的LSCN指标算法，由实验结果我们可以看出其在多个不同网络中的预测效果得到很大提升.同时我们对LSCN指标进行改进，进一步提出了基于二阶邻节点结构相似度的LSCN-Ⅱ指标.通过对不同的网络数据集选取最佳α参数，从而使得最终结果与LSCN指标相比得到进一步提升.

但是仅考虑邻居节点的相似度指标在链路预测中必定有一定的局限性，虽然计算复杂度低但是在预测准确度上不能有很大提高.并且通过第二章的介绍我们可以看出，各算法的预测效果很大程度上依赖于不同网络模型在真实网络中所占的比例.因此下一步我们希望通过进一步区分不同节点所属的网络模型，以及结合现在比较热门的有向加权网络结构特征，使得算法的预测效果得到进一步提升.

[1] Lv Lin-yuan.Link prediction on complex networks[J].Journal of University of Electronic Science and Technology of China，2010，39(5)：651-660.

[2] Xiao Han，Wang Le-ye，Son N.Han.Link prediction for new users in social networks[C].Proceeding of 2015 IEEE International Conference on Communications (ICC 2015)，London，2015：1250-1255.

[3] Lv L，Zhou T.Link prediction in complex networks：a survey[J].Physica A：Statistical Mechanics and its Applications，2011，390(6)：1150-1170 .

[4] Brin S，Page L.The anatomy of a large-scale hypertextual web search engine[J].Computer Networks and ISDN Systems，1998，30(1)：107-117.

[5] Saruukkai B R.Link prediction and path analysis using markov chains[J].Computer Networks，2010，33(1-6)：377-386.

[6] Liu Z，Zhang Q M，Lv L，et al.Link prediction in complex networks a local naive Bayes model[J].Europhysics Letters，2011，96(4)：48007-48012.

[7] Sharma D，Sharma U.Link prediction algorithm for coauthorship networks using neural network[C].Proceeding of the 3rd International Conference on Reliability，Infocom Technologies and Optimization (ICRITO 2014)，Noida：2014，1-4.

[8] Clauset A，Moore C，Newman M E J.Hierarchical structure and the prediction of missing links in networks[J].Nature，2008，80(4)：98-101.

[9] Shang M S，Lv L，Zhang Y C，et al.Empirical analysis of web-based user-object bipartite networks[J].Europhysics Letters，2010，90(4)：1303-1324.

[10] Zhang Yang-fu.Link prediction in directed and weighted networks[D].Xiangtan：Xiangtan University，2011.

[11] Salton G，Mcgill M J.Introduction to modern information retrieval[J].Auckland：MuGraw-Hill，1983，41(4)：305-306.

[12] Leicht E A，Holme P，Newman M E.Vertex similarity in network[J].Physical Review E Statistical Nonlinear and Soft Matter Physics，2006，73(2)：026120-026129.

[13] Sorensen T A.A method of establishing groups of equal amplitude in plant sociology based on similarity of species content and its application to analyses of the vegetation on Danish commons[J].Biol Skr，1948，5(4)：1-34 .

[14] Ravasz E，Somera A L，Mongru D A，et al.Hierarchical organization of modularity in metabolic networks[J].Science，2002，297(5586)：1551-1555.

[15] Zhou T，Lv L，Zhang Y C.Predicting missing links via local information[J].The European Physical Journal B- Condensed Matter and Complex Systems，2009，71(4)：623-630.

[16] Adamic L A，Adar E.Freiends and neighbors on the web[J].Social Networks，2003，25(3)：211-230.

[17] Barabási A L，Albert R.Emergence of scaling in random networks[J].Science，1999，286(5439)：509-512.

[18] Lv L，Jin C H，Zhou T.Similarity index based on local paths for link prediction of complex networks[J].Physical Review E Statistical Nonlinear & Soft Matter Physics，2009，80(2)：593-598.

[19] Liu Da-wei，Lv Yuan-na，Yu Zhi-hua.An improved link prediction algorithm for complex networks[J].Journal of Chinese Computer Systems，2016，37(5)：1071-1074.

[20] Hanley J A，McNeil B J.A method of comparing the areas under receiver operating characteristic curves derived from the same cases[J].Radiology，1983，148(3)：839-843.

附中文参考文献：

[1] 吕琳媛.复杂网络链路预测[J].电子科技大学学报，2010，39(5)：651-660.

[10] 张扬夫.有向与加权网络的链路预测[D].湘潭：湘潭大学，2011.

[19] 刘大伟，吕元娜，余智华.一种改进的复杂网络链路预测算法[J].小型微型计算机系统，2016，37(5)：1071-1074.