滑坡涌浪对坝面冲击压力的影响因素研究

李 静，陈健云，徐 强，孙 迅

（大连理工大学 建设工程学部，辽宁 大连 116024）

1 研究背景

汶川地震导致西南震区发生了大量的边坡失稳，即使当时未直接失稳破坏，但由于强震损伤严重，降低了边坡的抗滑稳定能力，近年来在不断发生的余震以及强暴雨等作用下，边坡失稳也在不断发生。显然，如果这一灾害发生在库区，滑坡体瞬时冲击库水将会引发巨大的涌浪，对挡水坝体造成冲击压力作用并威胁下游人民生命和财产安全。

我国西南地区工程地质条件多为高陡边坡，滑坡涌浪问题日益突显出来。因此，对于西南高坝大库，特别是狭长型河谷水库，不仅要考虑强震对坝体的损伤破坏，还要考虑强震或暴雨引发的滑坡涌浪对大坝冲击造成的灾害叠加风险。历史上多次滑坡涌浪造成了严重的结构破坏，如1959年意大利庞特塞拱坝库区大约300万m3的滑坡引发的漫顶涌浪高达20多米。1961年拓溪水电站大坝上游右岸山体滑坡，造成约165万m3的土石体以20 m/s的速度涌入水库，漫过正在施工的溢流坝段坝顶的涌浪高度为3.6 m。1963年意大利瓦伊昂拱坝库区内滑坡导致300万m3的土石冲入200多米水深的狭窄河谷内，形成的涌浪在漫过坝顶时仍有100多米高，在下游距离大坝1.4 km的河口出口处立波仍然高达70 m，冲毁了大部分朗格尼亚镇。

由于滑坡涌浪的巨大危害，围绕着滑坡涌浪首浪高度与滑坡体相关参数之间的关系，基于经验公式、物理模型试验以及数值分析开展了大量的研究。谷建［1］采用潘家铮法分析了某水电站滑坡涌浪不同滑速下的涌浪高度。庞昌俊［2］通过试验研究了边坡坡度、体积和入水速度等因素对滑坡涌浪的影响。殷坤龙等［3］根据体积守恒和水下滑块运动，将滑坡涌浪分成体积涌浪部分和冲击涌浪部分。吴佳壕［4］对小湾水电站进行了涌浪分析。徐文杰［5］采用数值方法研究了滑块形状、体积、滑面摩擦系数、水面宽度等因素对滑坡涌浪及爬坡高度的影响。缪吉伦等［6］对刚性滑块入水涌浪进行了分析。目前的研究主要是通过经验公式对涌浪浪高及其爬坡进行计算，使用数值模拟对涌浪过程进行自由面追踪，而对于涌浪对挡水建筑物冲击作用力方面的研究相对较少。黄锦林［7］通过模型试验对坝面滑坡涌浪冲击压力分布进行了测试。杨艳［8］则通过水工模型试验，研究了滑坡涌浪对架空直立码头的正面波压。

本文针对滑坡体入水过程的涌浪生成及传播过程进行数值模拟，分析不同因素对涌浪要素、传播过程及坝面冲击压力特征的影响。

2 基于SPH方法的滑坡涌浪分析

2.1 SPH方法基本理论光滑粒子水动力学方法（the Smoothed Particle Hydrodynamics，SPH）将分析区域离散为光滑核函数加权的粒子（如图1所示）［9］。将流体动量方程离散成粒子形式，则可以得到流体基于SPH方法的方程：

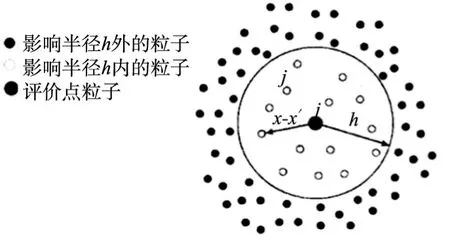
图1 SPH分析模型

式中：vi为粒子i的速度；t为时间；N为粒子j支持域内粒子总数；p为压力；ρj、mj为粒子j的密度和质量；Ñ为梯度算子；为粒子i和粒子j之间的距离；h为光滑长度；为表征粒子j对粒子i影响的核函数［10］，满足归一化、紧支性及狄拉克函数等条件，本文选取三次B样条函数；Πij为黏性力项。

对任意一个粒子i，本文采取连续性密度法，将连续方程离散成粒子形式［11］：

通过式（2）得到的粒子密度决定了粒子分配和光滑长度h的变化。

粒子压力根据粒子密度采用流体状态方程计算，本文采用Mie-Gruneisen状态方程：

式中：ρ0为粒子初始密度；C及S1、S2、S3为与冲击波波速Us与波后质点粒子速度Up相关的常数［12］；γ0为Gruneisen常数；α为γ0的一阶体积修正系数；μ=ρρ0-1；E为初始内能，在常温下取值为0。

黏性力项通过下式得到［13］:

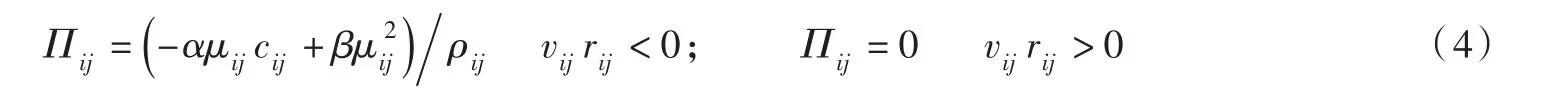
光滑长度h的选择关系到计算效率和计算精度，太小会降低计算效率，太大会丢失局部特性。本文通过平均密度来对光滑长度进行调节变换：

式中：h0为初始的光滑长度；ρ0为初始密度；d为空间维数。

由于在边界上的粒子存在缺陷，并且会发生积分截断的现象，本文采用耦合边界法［14］，设置两层固壁粒子来模拟固壁边界。积分时间步长需满足Courant-Friedrichs-Levy（CFL）条件。本文使用简单经典的一阶格式用于积分，时间步长由下式决定：

式中：KCFL为数值常数，一般取0.3。

库区流体SPH粒子与滑块有限元单元的耦合采用基于法向罚函数的点面接触算法。

2.2 滑坡涌浪数值分析模型剖面如图2所示，长300 m，深50 m，滑块单元尺寸和水体粒子间距均为1 m，图2中右边界为固定边界，上游为无反射边界。滑块体尺寸为10 m×20 m×50 m（长×宽×高），滑块距离左端边界2 m（如图2所示）。滑块初速度和到达底部速度均为0 m/s。为了探讨粒子间距的影响，本文分别对1、2和5 m粒子间距模型进行了模拟。

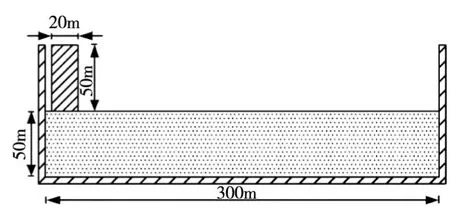
图2 模型剖面

数值模型主要参数参考文献［12］中的数值，具体如表1所示。

表1 水体Gruneisen状态方程主要参数

图3为涌浪产生和传播过程。从图3中可以看出，滑坡体入水后，水体受到滑坡体挤压，两侧水体迅速升高，右侧水体与滑坡体分离，随后形成反向卷入波，随滑坡体进入水体的大量空气在坡体右下侧形成空腔，进一步抬高液体表面高度。在滑块到达水底后，由于重力作用，气泡发生破碎，能量耗散下波浪稍有回落向右传播。随后回涌的水体与滑块相撞，再次成浪向右传播。首浪传播至右端坝面后爬坡到最大值，然后发生明显回落。

以上现象在粒子间距1 m和2 m时都可以观察到，粒子间距5 m则过于粗糙，反向卷入波和气体空腔现象不明显，观察不出水体的运动变化特性，自由面波形变化也由于粒子过于稀疏不能很好呈现。

图3 涌浪传播过程

图4为滑坡体下落位移及速度随时间的变化曲线。从图4可以看出，滑坡体滑入水中后速度逐渐变大，然后逐渐变小。到达底部后，滑块位移与速度均有些微的震荡，最终趋于静止，这个现象更符合实验结果和实际情况［15］。

采用不同的粒子间距参数得到的滑块下落位移曲线几乎一致，都能反映滑块的运动特性。不过粒子间距较大时，滑块会更早的受到边界的排斥力作用，到达水底的时间略微延后。

图5为右侧边界的涌浪冲击压力包络分布图。由图5可见，1 m和2 m粒子间距得到的边界最大冲击压力沿高度的分布基本一致，下部略有差别。涌浪作用下，坝面最大冲击压力部位在水表面附近，并且远超过静水压力，甚至比库底静水压力还要大。5 m的粒子间距过大，不能合理反映冲击压力的分布规律。说明在粒子稀疏的情况下，SPH粒子的偶然性和不均匀性大大提高，不足以正确反映水体粒子的运动特性。

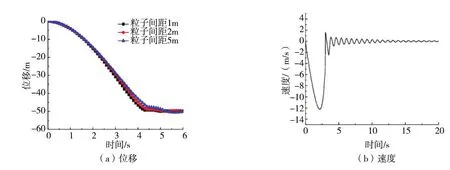
图4 滑块下落过程时间曲线

滑坡入水点不同距离的涌浪高度随时间的变化如图6所示。从图6可以看出，距离滑坡入水点较近部位的初始涌浪高度较大，距离稍远处由于受到气泡破碎、浪体回涌的影响而小于最大浪高。由于沿程能量损失，在传播过程中涌浪高度缓慢衰减，平稳浪高要小于初始最大浪高。说明稳定涌浪呈现近似孤立波形态传播。

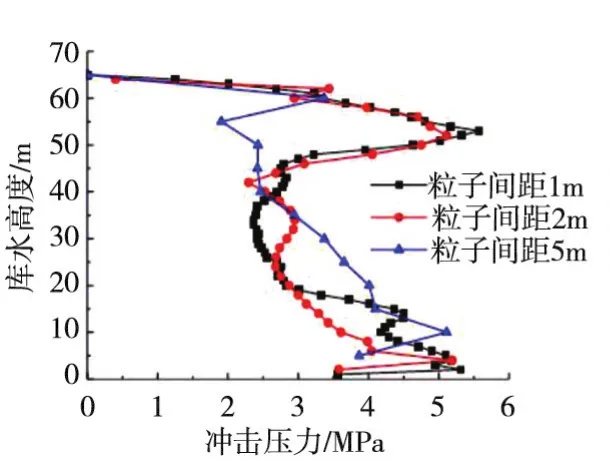
图5 坝面涌浪冲击压力包络图

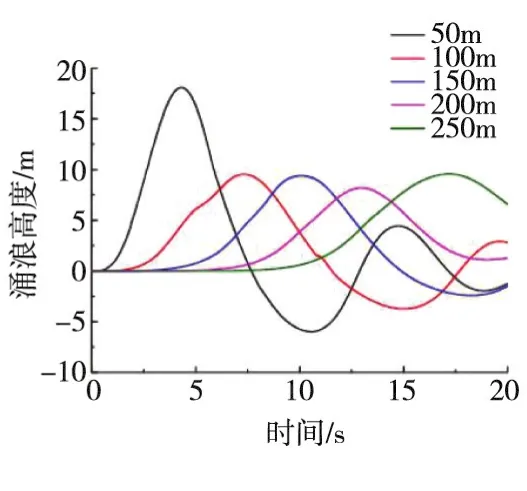
图6 不同距离处自由面曲线

2.3 自由面波形对于经典孤立波，假定波幅远小于水深，则水面线方程为：

式中：y为水面高程；a为波幅；L为长度标量，L=d 4d 3a，d为水深。孤立波的重力势能为：

式中：b为滑块宽度；l为滑块长度；ρ为水体密度。

假定滑块重力势能均转化为孤立波的能量，有：

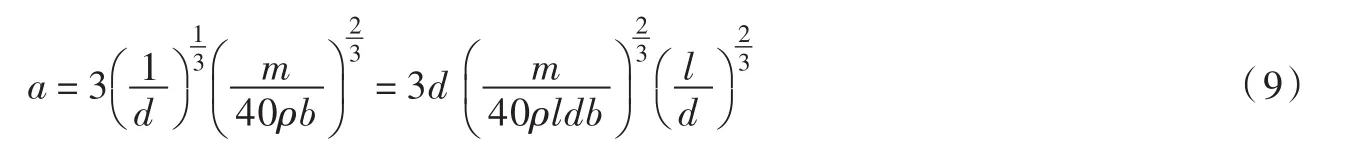
其中：m为滑块质量。

代入Boussinesq方程［16］，可以得到孤立波波形的解析解为：

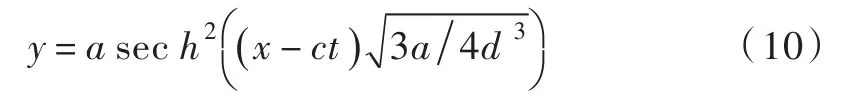
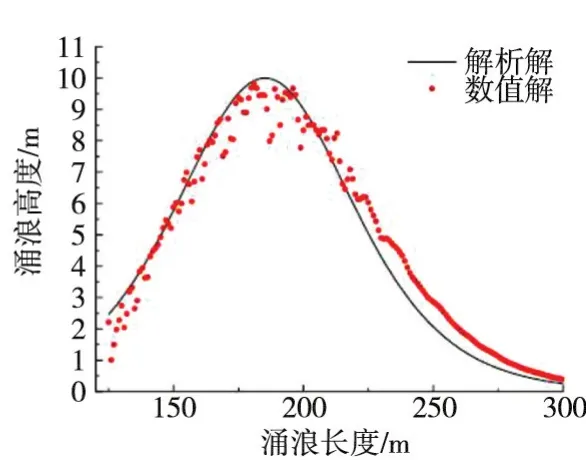
图7 自由面波形

图7为应用前文所述的SPH方法计算的t=10s时自由面波形数值模拟结果与式（10）得到的解析解波形对比。从图7可见，数值模拟结果与解析解吻合良好，说明本文数值模型分析结果是可靠的。

3 影响因素分析

3.1 滑坡体初始入水速度对涌浪及冲击压力的影响我国西部水电工程位于高山峡谷地区，山高坡陡，来自于不同高度的滑坡体的入水速度是不同的，本文以库水水深为70 m为例，对滑坡体入水速度分别为0、10及20 m/s情况下涌浪波高及坝面冲击压力进行比较研究。滑坡入水的形式有很多，不同的入水方式会对首浪高度以及涌浪传播产生影响。由于本文的重点在于研究涌浪对于坝体表面的冲击作用，从水库涌浪产生本身来讲，都可以等效为边界冲击条件和初始条件，因此计算中采用简化的垂直入水得到不同的入水速度和入水体积的影响。

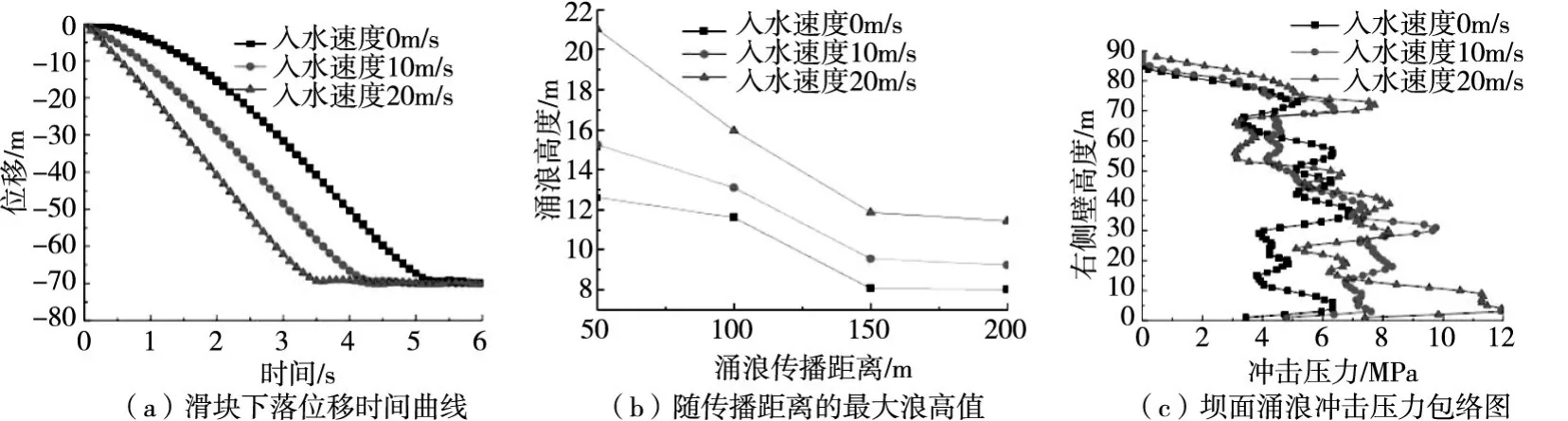
图8 不同入水速度影响比较

图8分别为滑坡体不同入水速度的位移-时间曲线、沿程最大浪高幅值曲线及坝面涌浪冲击压力包络分布。由图8可见，随着滑块入水速度的增大，滑块到达底部的时间大大缩短，沿程涌浪幅值增加。涌浪对坝面的冲击压力幅值在坝面上部和下部随着入水速度的增加而增加，但是在坝面中部冲击压力随入水速度增加呈不规则变化。

3.2 滑坡体宽度对涌浪及冲击压力的影响滑坡体入水形态与宽度有关，本文以40、30和20 m三种尺寸为例研究滑坡体宽度对涌浪及冲击压力的影响。滑块尺寸（长×宽×高）分别为10 m×40 m×25 m、10 m×30 m×33.33 m和10 m×20 m×50 m，水深25 m。

图9分别为不同滑坡体宽度下的位移-时间曲线、沿程最大浪高幅值曲线及坝面涌浪冲击压力包络分布。从图9可见，体积不变条件下，随着滑坡体宽度增加，入水阻力增大，入水过程明显变得缓慢，首浪最大波高降低，稳定波高沿着传播途径的衰减速率减小。当传播距离超过100 m后，涌浪稳定浪高随着滑坡体宽度的增加而增大。不同宽度下形成的涌浪对坝面的冲击压力分布基本上一致，幅值随着滑坡体宽度的增加而增加。

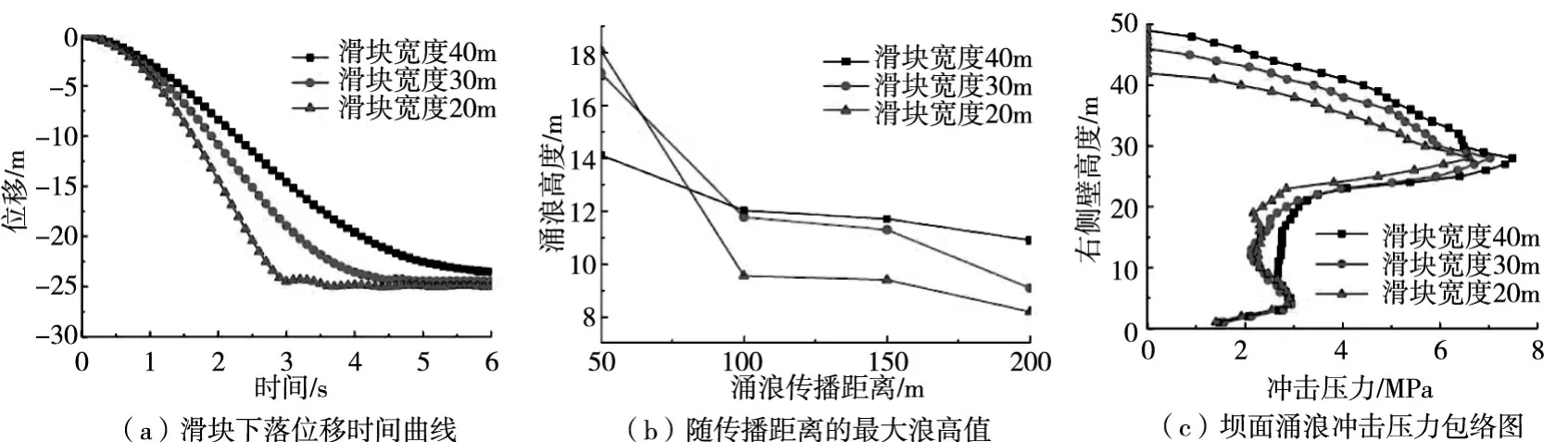
图9 不同滑块宽度影响比较

3.3 库水水深对涌浪及冲击压力的影响本文分别对25、50和70 m三种不同库水深度下的涌浪及其作用进行分析，结果如图10所示。

从图10可见，水深不影响滑坡体在水中的运动速度。由于滑坡体体积和入水速度相同的情况下，随着水深增加，滑坡体传递给水体的能量向滑坡体下部深处增加，水平向挤压产生的首浪最大浪高减小，说明在浅水情况下，滑坡更易形成较高的首浪波高，对于距离滑坡较近的大坝冲击是不利的。但是随着涌浪向挡水坝面的传播，不同水深情况下的涌浪稳定波高逐渐趋向一致。

从坝面涌浪冲击压力的分布也可以看出，不同水深情况下，最大冲击压力在坝面中上部的分布以及最大幅值基本上一致。但是随着水深的增加，冲击压力在中下部的变化呈波动性多峰值分布，说明由于滑坡冲击在深水情况下能量传递的复杂性，对于坝面的冲击压力有不利影响。

图10 不同库水深度影响比较

4 涌浪对挡水重力坝的影响

4.1 不同水位下坝前涌浪形成及传播过程经过加固后的库区边坡通常具有较好的抗滑稳定能力。但是，经历强震作用后的边坡抗滑稳定能力会降低。如果强震中受损的边坡在强余震或者强暴雨发生失稳，其次生灾害主要是对强震中同样受损的挡水坝体的涌浪冲击作用。

在滑坡涌浪浪高较大或者坝前水位较高时，涌浪有漫过坝顶的情况，本文基于SPH-有限元耦合分析模型，分别研究低水位和高水位两种情况下的滑坡涌浪冲击作用，模型如图11所示，数值模型中采用的主要参数如表2所示。

图11 模型剖面

表2 主要材料参数

计算坝体高度103 m，库区水体模拟区域长300 m，水深分别为70和100 m。滑坡体体积为10 m×20 m×50 m，入水速度为0 m/s。

图12为库区涌浪传播过程。从图12可以看出，高水位和低水位情况下，涌浪产生和传播过程与前面的分析基本上类似，随着滑坡体下落，右侧库水被推挤迅速向右运动，随后卷入波产生、越过滑块、向左回涌、滑块右侧下部形成气体空腔随滑块向底部运动等现象渐次发生。然后气体空腔减小、消失，回涌水体冲击到左侧边界开始向上爬升，然后回落再次形成新的波浪向右传播，在右侧坝面上爬升的涌浪开始回落。

在70 m低水位下最大浪高为12.74 m，在坝前没有越过坝顶；100 m高水位情况下，最大浪高约11.24 m，10 s时坝前涌浪已开始漫上坝顶，随后涌浪漫过坝顶，涌入下游，冲击大坝下游面。

图12 库区涌浪传播过程

4.2 不同水位下滑坡涌浪冲击下的坝体位移图13为坝顶顺河向位移时程。由图13可知，两种水位下坝体受到的流体冲击过程类似。首先受到的是快速传播的压缩波作用（波速1440 m/s），这是滑坡入水对库水的瞬间冲击产生的，对坝面形成第一次作用，坝体在压缩波作用下发生较大动态位移，随后振动幅度逐渐衰减。在8.2s左右，滑坡产生的涌浪重力波（波速28～33 m/s）传播到坝前，在涌浪冲击下坝体振动位移再次增加，随后振动幅度逐渐衰减。高水位下，10s左右涌浪爬坡越过坝顶冲向下游，涌浪作用下的坝体位移振动平衡位置逐渐偏移。

图13 坝顶点位移-时间曲线

4.3 不同水位下滑坡涌浪冲击下的坝体拉应力图14为滑坡库水冲击下坝踵和下游折坡点的第一主应力变化时程曲线。从图14可见，低水位下的坝体应力在涌浪冲击作用下比库水压缩波动压力作用下的大，而高水位下相反。这一方面是因为滑坡入水过程中，滑坡体冲击库水传递的压缩波动能量与挤压库水传递的涌浪重力波动能量在不同的水深条件下不同，另一方面是高水位下，由于涌浪越过坝顶就降低了涌浪冲击压力的影响。

图14 坝踵与下游折坡点第一主应力时程曲线

坝踵和下游折坡点应力均在压缩波和涌浪冲击到达时最大，随后衰减，相比而言，高水位下由于涌浪越坝使得涌浪回涌减少，下游折坡点的应力衰减更快；下游折坡点在库水冲击作用下的应力增加幅度远远大于坝踵，说明滑坡引起的库水冲击压力对坝体中上部影响更大，坝头部位更为危险。

4.4 库水冲击压力分析当前研究滑坡涌浪对挡水结构的冲击压力作用开展的相对较少，有限的研究也主要集中在滑坡入水引起的涌浪波特征及其作用上。实际上，滑坡对库水的影响包括两部分，一部分是滑坡入水对库水边界冲击引起的流体体积压缩波，波速为1440 m/s；一部分是滑坡体挤压库水形成的流体表面重力波，在本文中传播波速为28～33 m/s之间；由于波速的差异，压缩体积波首先传播到坝面形成冲击，随后是涌浪冲击作用。两种波的幅值和坝面分布形式是不同的。图15为大坝上游面压力。从图15（a）可以看出，由于压缩波为流体的机械波动，其作用范围在库水静水位以下，并且在水表面为零。而涌浪为表面重力波，其作用范围与涌浪在坝面的爬升高度有关；从图15（b）可以看出，其作用范围高出静水位线超过12 m，由于涌浪冲击作用性质，即使在水表面也具有很大的作用幅值。

图15 大坝上游面压力

在缩尺模型试验中由于库水相似材料选择的限制，很难同时满足两种波动的相似率设计要求，由于压缩波波速很快，缩尺条件下通常只能测得涌浪的生成、传播和作用，很难测到压缩波的传播特征和影响。而在实际工程中库区尺度相对较大，大坝同时受到两种库水冲击的先后作用，在实际中是不能忽视库水压缩波冲击作用的影响的。实际上，由于两者的强度、坝面分布形式均不相同，压缩波冲击作用对大坝也有很大的影响。特别是两种冲击波是具有不同周期特性的动力作用。按照坝面涌浪压力分布采用静力计算的方法分析坝体动力响应可能是偏于危险的。

5 结论

针对水利枢纽库区边坡失稳诱发的库水冲击问题，分析了滑坡涌浪的产生、传播以及对坝面冲击压力的作用特征，研究了滑坡入水速度、库水水深和滑块宽度等因素对以上特征的影响，并分别针发生漫顶和不漫顶的两种水位下的坝体动力响应特征进行了分析。本文得到以下结论：（1）基于SPH方法的粒子间距选择必须满足不同波动的波长要求，过大的粒子间距无法捕捉流体的正确波动形态。通过与解析解的对比，得到的坝面冲击压力作用以及对坝体位移和应力的分析是合理的，说明本文的分析模型是可靠的。（2）滑坡体参数及库水深度等因素对于涌浪生成及传播过程的定性特征影响不大，但是对于坝面的冲击压力强度和分布特征影响很大。（3）库区滑坡入水会引发库水机械波和重力波的冲击作用。两种波的传播速度差异接近2个数量级，坝体先后受到库水压缩波和涌浪的冲击作用。压缩波冲击作用在静水位以下，静水位部位冲击压力为零；涌浪冲击作用范围在涌浪自由表面以下，在靠近水位线附近强度最大。（4）坝体上部在冲击波作用下的应力增大幅值远远大于中下部，不过由于静力作用下坝踵部位为拉应力薄弱部位，因此，库水冲击作用下坝踵和坝头部位都为危险薄弱部位。（5）涌浪冲击作用起主要作用，但由于两种冲击作用的动力特性以及在坝面的分布形式不同，对于坝体不同部位动力响应的影响规律是不同的，在实际工程中不能忽视压缩体积波冲击作用对坝体动力破坏的影响。

库水冲击作用对坝体的影响与滑坡体入水的形式、形态、体积、速度、角度以及库水深度、滑坡体入水点与坝体的距离、坝体与库水的相对高度、坝体动力特性等很多因素有关，本文只研究了主要影响因素中的几个，其他相关因素的影响还有待于进一步深入研究。

［1］谷健.某水电站库区变形体滑坡涌浪初步分析［J］.水电站设计，2013，29（4）：56-59.

［2］庞昌俊.二维斜滑坡涌浪的试验研究［J］.水利学报，1985（11）：54-59.

［3］殷坤龙，杜娟，汪洋.清江水布垭库区大堰塘滑坡涌浪分析［J］.岩土力学，2008，29（12）：3266-3270.

［4］吴佳壕.山区河道型水库库岸坡涌浪灾害研究与预测［D］.成都：成都理工大学，2011.

［5］徐文杰.滑坡涌浪影响因素研究［J］.工程地质学报，2012，20（4）：491-507.

［6］缪吉伦，陈景秋，张永祥 .基于SPH方法的立面二维涌浪数值模拟［J］.中南大学学报（自然科学版），2012，43（8）：3244-3249.

［7］黄锦林.库岸滑坡涌浪对坝体影响研究［D］.天津：天津大学，2011.

［8］杨艳.山区河道型水库滑坡涌浪对架空直立式码头结构作用影响研究［D］.重庆：重庆交通大学，2014.

［9］QIU L.Two-dimensional SPH simulations of landslide-generated water waves［J］.Journal of Hydraulic Engineer⁃ing，2008，134（5）：668-671.

［10］GÓMEZ-GESTEIRA M，DALRYMPLE R.Using a three-dimensional smoothed particle hydrodynamics method for wave impact on a tall structure［J］.Journal of Waterway，Port，Coastal and Ocean Engineering，2004，130（2）：63-69.

［11］AMINI Y，EMDAD H，FARID M.A new model to solve fluid-hypo-elastic solid interaction using the smoothed particle hydrodynamics（SPH）method［J］.European Journal of Mechanics-B/Fluids，2011，30（2）：184-194.

［12］MONAGHAN J J，GINGOLD R A.Shock simulation by the particle method SPH［J］.Journal of Computational Physics，1983，52（2）：374-389.

［13］COLAGROSSI A，LANDRINI M.Numerical simulation of interfacial flows by smoothed particle hydrodynamics［J］.Journal of Computational Physics，2003，191（2）：448-475.

［14］张姝慧.求解浅水波方程的光滑粒子流体动力学法［D］.合肥：安徽大学，2007.

［15］YIM S，YUK D，PANIZZO A，et al.Numerical simulations of wave generation by a vertical plunger using RANS and SPH models［J］.Journal of Waterway，Port，Coastal and Ocean Engineering，2008，134（3）：143-159.

［16］李孟国，王正林，蒋德才.关于波浪Boussinesq方程的研究［J］.青岛海洋大学学报（自然科学版），2002，32（3）：345-354.