水库中长期发电优化调度解析方法及应用

陈森林，梁 斌，李 丹，陶湘明

（1.水资源与水电工程科学国家重点实验室，湖北 武汉 430072； 2.武汉大学 水利水电学院，湖北 武汉 430072；3.中国电建集团 成都勘测设计研究院有限公司，四川 成都 610000）

1 研究背景

水库中长期发电优化调度是实现水能资源高效利用的重要技术手段，也是水电站及其水库制定和实施中长期运行计划的核心问题。随着运筹学、系统工程及智能算法的逐步引入，水库中长期发电优化调度模型的求解方法和调度规则的研究得到了快速的发展。

在水库发电优化调度模型求解的众多方法中，动态规划算法（Dynamic Programming）以其适用于多时间段序贯决策并能灵活处理非线性、不连续优化模型等特点而在水库调度领域得到了广泛应用［1］。随着大量水库电站的建成和投入使用，优化算法的研究也由针对单个水库或单个目标向梯级水库和多目标转变。为了避免库群系统优化调度模型求解的“维数灾”问题，相关专家和学者对传统动态规划算法进行了诸多改进。赵铜铁钢等［1］分析了水库调度目标函数的凹性和决策的单调性，提出了搜索域缩减算法和邻域搜索算法。Tolson等［2］开发了一种全搜索域上产生初始解、通过迭代逐渐逼近局部空间内的动态降维算法。Zhang等［3］提出了基于动态规划算法与遗传算法的平行算法。纪昌明等［4］提出了基于泛函分析思想的动态规划算法。孙平等［5］提出了一种基于状态组合遍历和多层嵌套两种多维动态规划算法的求解模式。钟平安等［6］研究了场景树在水库调度随机规划中的应用。H.R.Howson［7］利用贝尔曼最优化原理，提出了渐近优化算法（Progressive Optimality Algorithm，POA）。以POA算法为依托，结合梯级调度的实际情况，相关学者对算法做了进一步的改进。李玮等［8］将大系统分解协调理论以及POA逐步逼近思想相结合对算法进行了改进。周佳等［9］运用惩罚函数和约束转换对POA算法进行改进。程春田等［10-11］提出了智能缩减系统求解规模策略和保证系统实用性的可视化交互法。冯仲恺等［12］结合正交试验设计方法提出了正交试验POA算法（OPOA）。张诚等［13］基于逐步差分和变阶段优化改进策略，提出了变阶段逐步优化算法。在智能算法方面，Schardong A等［14］提出了一种自适应多目标差分进化算法与网络流算法结合的混合算法。Haddad O B等［15］运用生物地理优化算法（BBO）来解决水库优化调度问题，在单库调度与多库联调计算中都取得了良好的调度效果。

由于库容曲线、水电站下游流量关系曲线采用离散值数值关系，使得水能计算中动力指标（库蓄水量、发电流量、发电水头及出力等）只能采用数值计算方法，从而导致传统优化调度模型的表达及其求解只能采用离散数值方法。针对这一问题，本文基于水库特性曲线的函数化，建立了水库中长期发电优化调度的解析函数模型，并基于POA算法原理提出了解析优化方法—APOA算法。通过狮子滩水库应用表明，APOA优化结果与POA相近，但计算效率显著提高。

由于目前难以证明不同水库的库容-水位关系和下游流量-水位关系符合某种函数型式，应用函数进行描述（称为“一次应用”）必然存在一定的拟合误差。但因水库中长期发电调度重点在于过程（库水位、出力等）和相关统计指标（发电量、用水量、保证率等），所以，发电调度（称为“二次应用”）的计算精度才是关键。

2 特性曲线和动力指标的函数表达

2.1 特性曲线的函数化表达

（1）水库库容-水位关系函数。由于出力公式中水头的计算需要由库容推求水库水位，因此，以库容为自变量、库水位为因变量的函数关系用三次多项式表达：

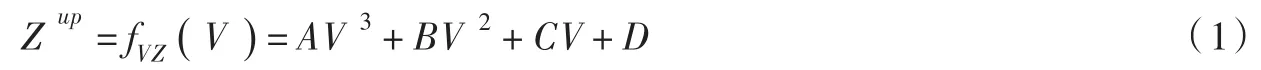
式中：Zup为水库水位，m；V为水库蓄水量（库容），（×l）m3；A、B、C、D为水库库容-水位关系函数的参数。

为了保证式（1）的拟合精度，Zup和V的数量级应该相当或接近，因此，水库库容宜取l=104、106或108的数量单位，并在水库调度方程中进行换算。

由于受测算方法和河床冲淤等影响，坝前水位以下水库的蓄水容积无法得到准确值，所以，水库调度计算中以数值形式表达的库容曲线并不是真实的水位-库容关系。同时，水库实际调度中，相对库蓄水量而言，库水位数值的准确性更受关注。

（2）水电站下游流量-水位关系函数。假设水库出流为水电站出流（出现弃水时再另外处理），下游流量水位关系一般可用二次多项式表示为：

式中：Zdown为水电站下游水位，m；Q为水电站发电流量，m3/s；a、b、c为下游流量-水位关系函数的参数。

（3）水电站发电流量-水头损失关系函数。由于受短期和厂内机组负荷分配及多方面计算条件的概化影响，中长期调度的水头损失属于一个统计值，但在水能计算中又不能完全忽略。因此，在水能规划或水电站实际运行中，水电站水头损失一般取固定值、或根据发电引水管道系统推求发电流量-水头损失关系的二次函数关系：

式中：ΔH为水电站水头损失，m；α为水电站发电流量-水头损失关系函数的参数。

（4）水电站预想出力-水头关系函数。预想出力为水电站实际运行中可能承担的最大出力（负荷），与水电站运行的净水头有关。净水头大于设计水头时，预想出力等于水电站装机容量，否则，预想出力与净水头成正比关系，可用分段线性函数关系表达：

式中：H、Hsj分别为水电站净水头和设计水头，m；Py、Pyx分别为水电站装机容量和水头H下的预想出力，kW；β为水电站预想出力-水头关系函数的参数。

2.2 水电站动力指标函数表达对任意一个时段t，如果已知时段初、末库蓄水量，基于水库特性曲线的函数关系，可以将水电站动力指标表示为函数形式。

（1）发电流量。由水库水量平衡方程可得发电流量：

式中：It、Qt分别为t时段平均入库流量和发电流量（暂不考虑弃水），m3/s；Vt-1、Vt分别为t时段初、末水库蓄水量，（×l）m3；λt为库蓄水量到流量的转换系数，

为t时段的时段长，h。

（2）水电站净水头。基于时段内要素线性变化假设和式（1）—（3），任一时段t水电站净水头为：

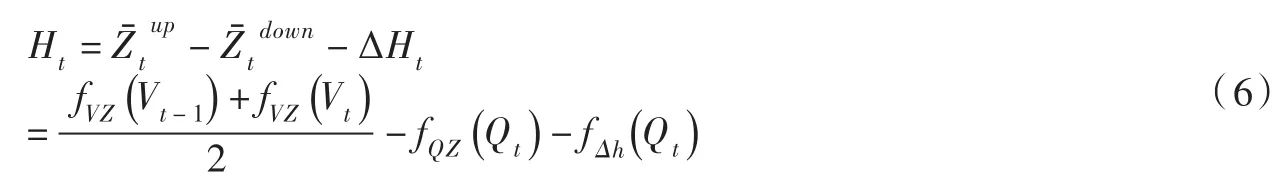
式中：Ht为t时段水电站净水头，m；、ΔHt分别为t时段平均库水位、下游水位及水头损失，m。

（3）水电站出力。根据出力公式和式（6），可得t时段水电站平均出力：

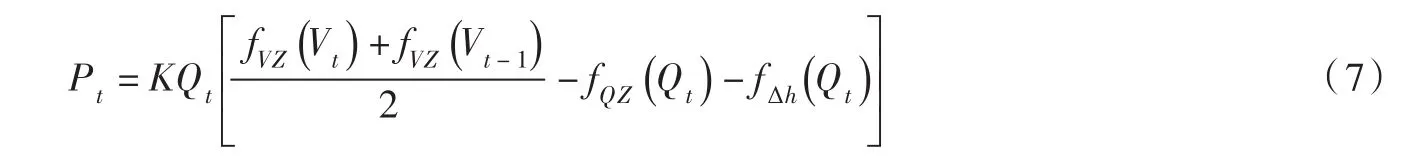
式中：K为水电站出力系数；Pt为水电站t时段平均出力，kW。

由式（7）既可由流量推求出力（“以水定电”显式计算），也可由出力推求流量（“以电定水”非线性函数方程迭代计算）。

3 水库中长期发电优化调度的解析函数模型

3.1 目标函数以水电站调度期总发电量最大为准则的目标函数为：

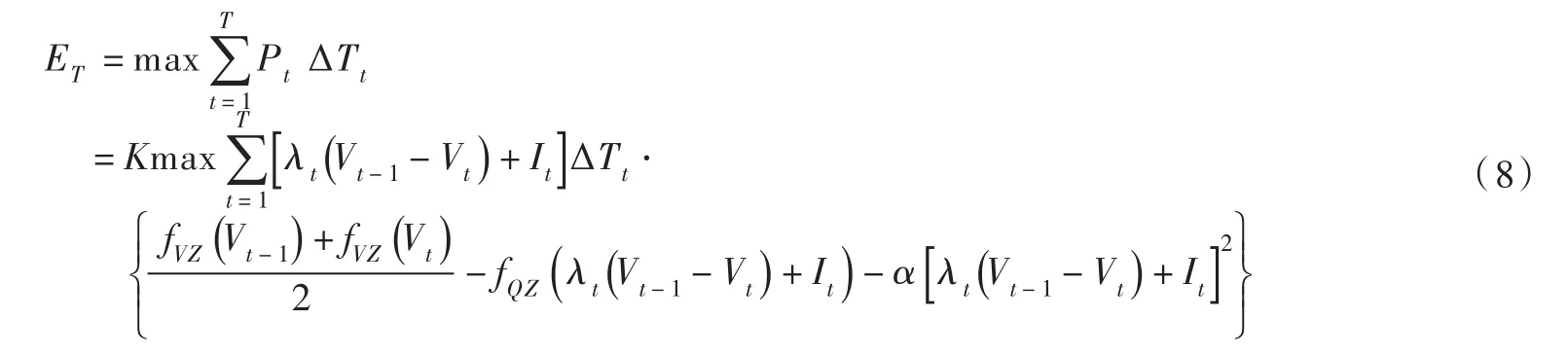
式中：T为调度期总时段数；ET为调度期最优总发电量，kW⋅h。

3.2 约束条件

（1）水库蓄水量约束。包括水库蓄水量的上、下限约束：

（2）综合利用约束。主要指通过发电产生的下游用水需求（上游用水可在式（5）考虑）：

式中：Qmint为t时段水库下泄流量的下限，m3/s。

（3）出力约束

水电站主要存在预想出力的Pmaxt限制，而电力系统则可能同时存在上下限限制，因此，式（11）是水电站和电力系统两种约束的合集。

（4）水库蓄水量边界约束。包括调度期初始和终止水库蓄水量约束：

式中：VBeg、VEnd分别为调度期初始和终止水库蓄水量，m3。

以式（1）—式（7）为基础，式（8）为目标函数，式（9）—式（12）为约束条件，构成了水电站中长期发电优化调度的解析函数模型（目标函数与约束条件均为解析函数）。值得注意的是，为了保证库水位和蓄水量计算的一致性，和VBeg、VEnd应根据相应的库水位由式（1）推求，不应采用原库容曲线插值得到的数值。

由式（8）可知，解析函数模型与传统优化数学模型主要区别在于两个方面：一是前者的动力指标全部通过函数计算，而后者则需要进行曲线插值等数值计算；二是前者将水库水量平衡约束耦合到目标函数，建立了以库蓄水量Vt为决策变量的非线性函数模型。

4 优化模型求解方法——APOA算法

由于突变型约束条件式（9）—式（11）的限制，该解析函数模型目前仍然难以整体解析求解。但基于水库水电站特点和约束条件的数学表达式，可以将约束条件合并为两类约束：一是“水量约束”，包含式（9）和式（10）；二是“出力约束”，包含式（11）。这两类约束均可以分别进行耦合处理。

在动态规划改进算法中，POA算法将全过程的优化分解为逐个二阶段优化问题，并应用一维搜索求解二阶段问题，既有效减少了决策变量的搜索空间，又回避了后效性问题。因此，我们借鉴POA算法的基本思路，提出了基于POA算法的解析方法（Analytic Progressive Optimality Algorithm，APOA），APOA与POA法的本质区别在于二阶段优化问题的求解方法，APOA采用单一变量的函数求极值方法（不需离散状态变量），而POA采用一维数值搜索方法。

由于式（9）—式（12）的约束导致解析函数模型的二阶段优化问题仍然难以直接求解，所以APOA法由二步算法组成：第一步，确定库蓄水量Vt，即以式（8）为基础建立二阶段优化模型，采用无约束函数（不考虑弃水）求极值方法，并考虑“水量约束”，推求“初步最优解”；第二步，确定两个时段的出力、发电流量及弃水流量，即如果“初步最优解”不能满足出力约束式（11），则按照一定规则对其进行修正（可能包括弃水流量计算），最终得到解析函数模型的最优解。

4.1 考虑“水量约束”的二阶段优化模型对于任意两个相连时段t和t+1，涉及3个时刻的库蓄水量Vt-1、Vt及Vt+1，从POA算法可知，Vt-1和Vt+1为已知值，而Vt为待求的优化决策变量。

（1）目标函数。根据式（8）可整理得二阶段优化问题的目标函数为：

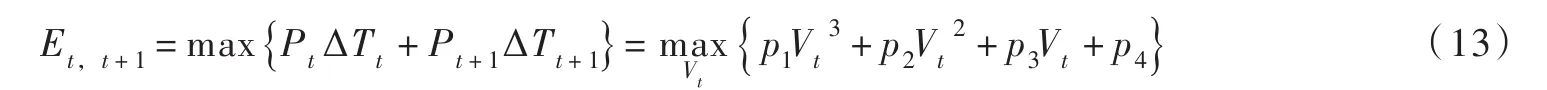
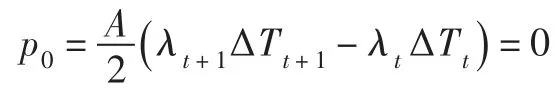
p4为常数项，由于不影响式（13）的极值点（或驻点）求解，可不做讨论；Wt和Wt+1为常数项，分别由下式计算：

由此可见，二阶段发电量最大模型的目标函数为Vt的一元三次多项式。

（2）约束条件。根据约束条件式（9）和式（10），可以确定同时考虑库蓄水量和综合利用约束下Vt的可行域。由式（5）和式（10）可得：

基于式（14），整理式（15）可得：

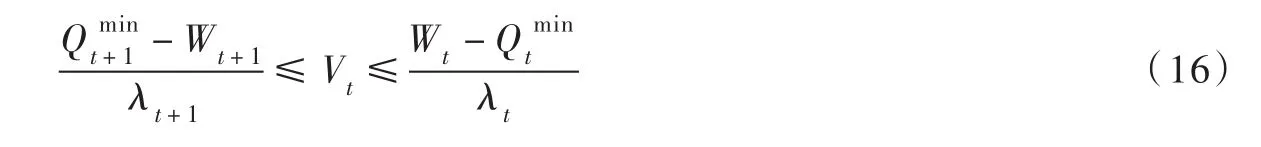
综合约束式（9）和式（16）可得：

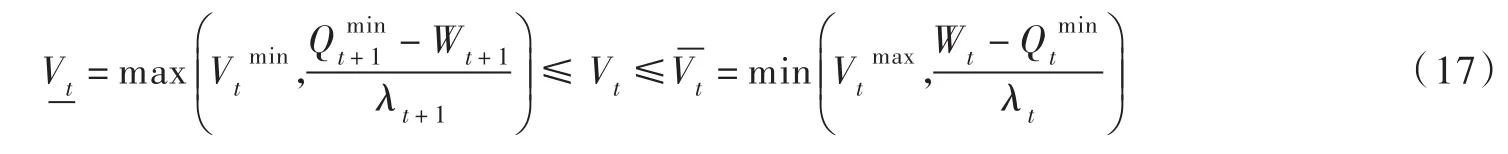
以式（13）为目标函数，式（17）为约束条件，就构成了考虑“水量约束”的二阶段优化数学模型。

4.2 二阶段优化模型求解方法如果出现，则说明二阶段问题无可行解（“初始解”存在或迭代计算中出现的），此时应保证t时段为可行解，即按照和取大值原则推求t时段出力和发电流量即可。否则，按以下方法推求。

应用式（5）可将式（13）的p1整理为：

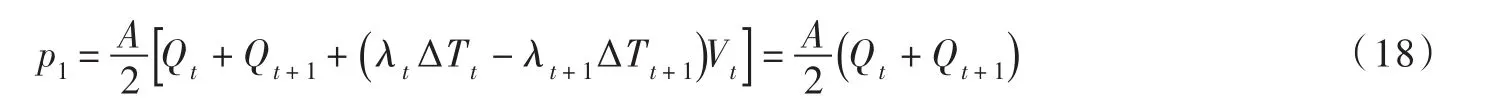
对式（13）求一阶导数，并令其等于0可得：

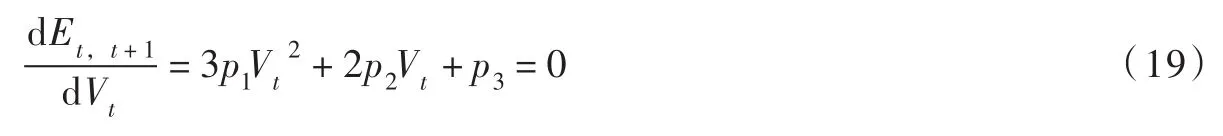
式（19）为二次多项式方程，其判别式为：

根据判别式（20）的取值不同，式（13）的“初步最优解”确定方法如下：

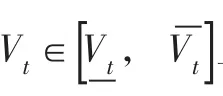
（2）若Δ>0，则式（19）在( )-∞,+∞上有两个不同实根ν1和ν2（不妨设ν1<ν2）：

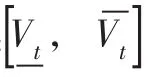
4.3 考虑出力范围约束的最优解根据“初步最优解”Vt，由式（7）可以计算两个时段的出力Pt和Pt+1。虽然Vt满足“水量约束”，但Pt和Pt+1还必须满足“出力约束”，这里先讨论出力范围约束。根据Pt和Pt+1与式（11）的出力范围，理论上可能存在9种组合情形（如表2所示）。通过多个实例水库实际年份长系列优化的计算结果统计，各水库在满足“水量约束”下“初步最优解”的每一个二阶段的出力组合占比情况如表3所示（其数值主要与各水库的径流过程、初始与终止水位及“水量约束”有关）。

表1 “初步最优解”确定方法

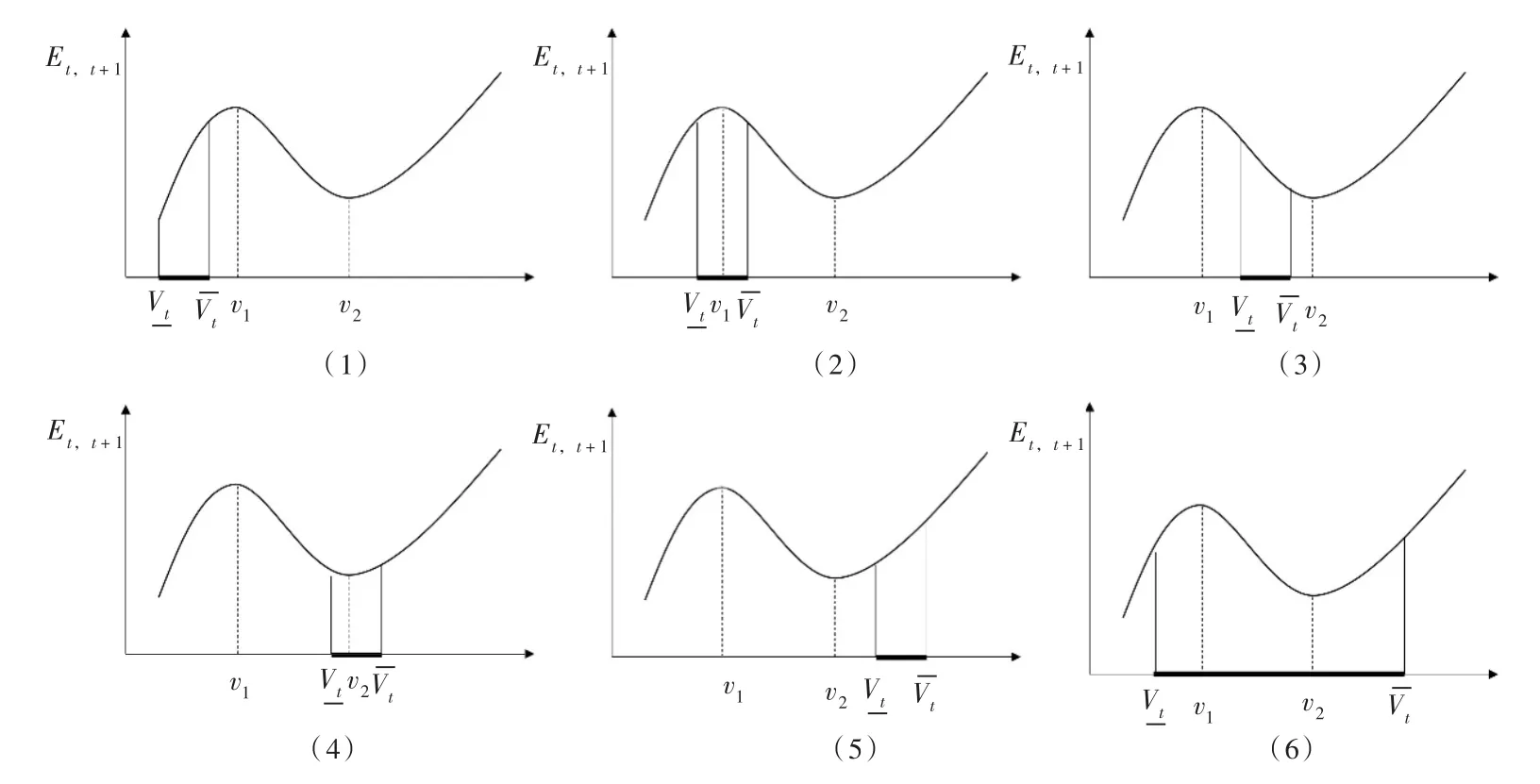
图1 极值点与可行域的位置关系

从表3的实例计算结果可知，主要集中于①②⑤，且从⑤所占比例来看，大部分情形下均不需要进行修正。其中，情形①②⑥主要出现在丰水期水库蓄水以抬高后期水位所致（参见图6）、情形④⑧则出现在枯水期消落段。因此，基于水库优化调度实际和POA算法原理，应优先保证t时段满足“出力约束”，如果t+1时段无法满足“出力约束”，可以留给下一个二阶段问题解决，因此，表2的9种情形可以分为5种处理类型：

表2 二阶段出力组合情形分类

（1）“不需要修正”型。情形⑤的“初步最优解”也满足“出力约束”，不需要修正；

（2）“二保一”型。情形①⑨应寻求Pt满足“出力约束”（放弃Pt+1约束，留待后续计算解决）；

（3）“优先保证”型。情形②⑧应优先保证Pt满足“出力约束”（可能引起Pt+1不满足约束，留待后续计算解决）；

（4）“二步修正”型。情形③⑦应首先保证Pt满足边界“出力约束”，可能直接转换为⑤，也可能分别转换为情形④⑥再继续调整；

（5）“全保”型。针对情形④⑥，应在保证Pt可行的条件下，寻求Pt+1也达到边界“出力约束”。

从POA算法的全过程顺序计算流程角度看，“出力约束”检验与“初步最优解”的修正方法，应该先判断t时段、后判断t+1时段，对每个时段先判断下限再判断上限，因此，表2的8种不可行情形可由以下（最多）4步方法进行修正：

图2 APOA的“初步最优解”修正算法流程

此外需要说明的是，每个二阶段优化问题，可以通过4次“以电定水”（最大、最小出力）计算，确定满足“出力约束”的Vt上下限，再与式（17）取交集得到，这样就不需要进行出力修正。由于“以电定水”需要迭代计算，计算效率较低，如果只用于少量时段的修正则更有利于提高计算效率。

5 实例应用及成果分析

狮子滩水库是重庆龙溪河梯级的龙头水库，具有多年调节能力，该水库以发电为主，兼顾防洪、灌溉、养殖、航运、旅游等综合利用任务。正常蓄水位为347 m，前汛期防洪限制水位346.3 m，后汛期防洪限制水位346.8 m，死水位为328.5 m，调节库容7.33亿m3。发电保证率为90%，保证出力为15 100 kW，装机容量为54 200 kW。水库特性曲线及拟合情况如图3和图4所示。

图3 库容-水位关系曲线

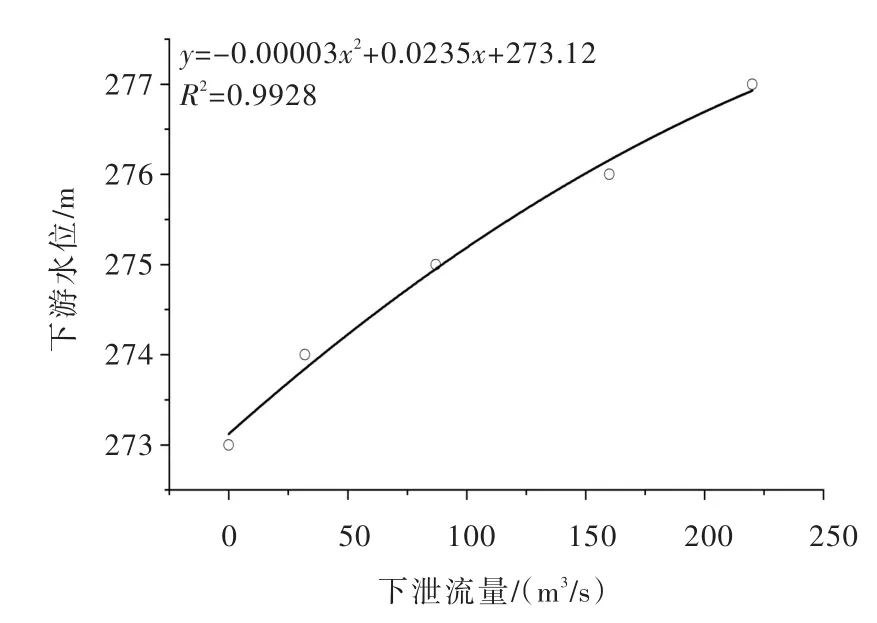
图4 下游流量-水位关系曲线

为了验证解析函数模型和APOA算法的科学性和高效性，本文分别针对典型年和长系列两种优化问题开展应用研究，并与POA算法的两种计算方案进行对比：（1）POA-Ⅰ算法。即传统的POA算法，库容水位以及下游水位流量关系的插值计算均采用分段线性插值，其二阶段优化过程和迭代递推过程使用离散状态变量的方法寻优。（2）POA-Ⅱ算法。与POA-Ⅰ的不同之处在于，采用式（1）和式（2）的库容水位以及下游水位流量关系函数计算。

5.1 典型年优化计算给定年初末水位均为死水位，分别选取10%、50%及90%水平年的入库径流（如图5所示），针对以上计算方案，可得到各种算法不同典型年的最优库蓄水位过程线（如图6所示，其中pre-APOA为仅满足“水量约束”的“初步最优解”过程）、水位误差（如图7所示）以及年发电量（如表4所示）。

（1）从表4可见，APOA算法与POA-Ⅰ算法的发电量相差仅0.03%～0.25%，水位过程相差最大不超过0.11 m（如图7所示），因此，对于水库中长期发电调度而言，解析函数模型及APOA算法几乎没有降低优化计算精度（受多种因素影响，POA算法的计算结果严格来说也不是真实最优解）。

（2）对比APOA和pre-APOA的蓄水过程（如图6所示）可知，不考虑“出力约束”的枯水年水位过程（最小出力按保证出力限制的最优解）全部高于考虑“出力约束”的过程，平水年和丰水年则比较接近，仅少数时段偏高。这种现象正确反映了水库前期力争蓄水、以抬高后期发电水头的客观规律。

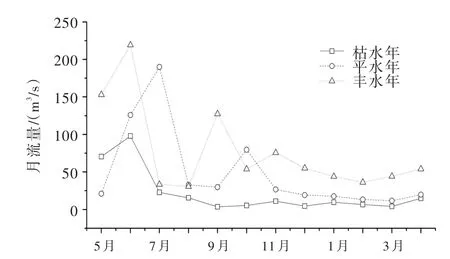
图5 狮子滩水库典型年逐月入库流量

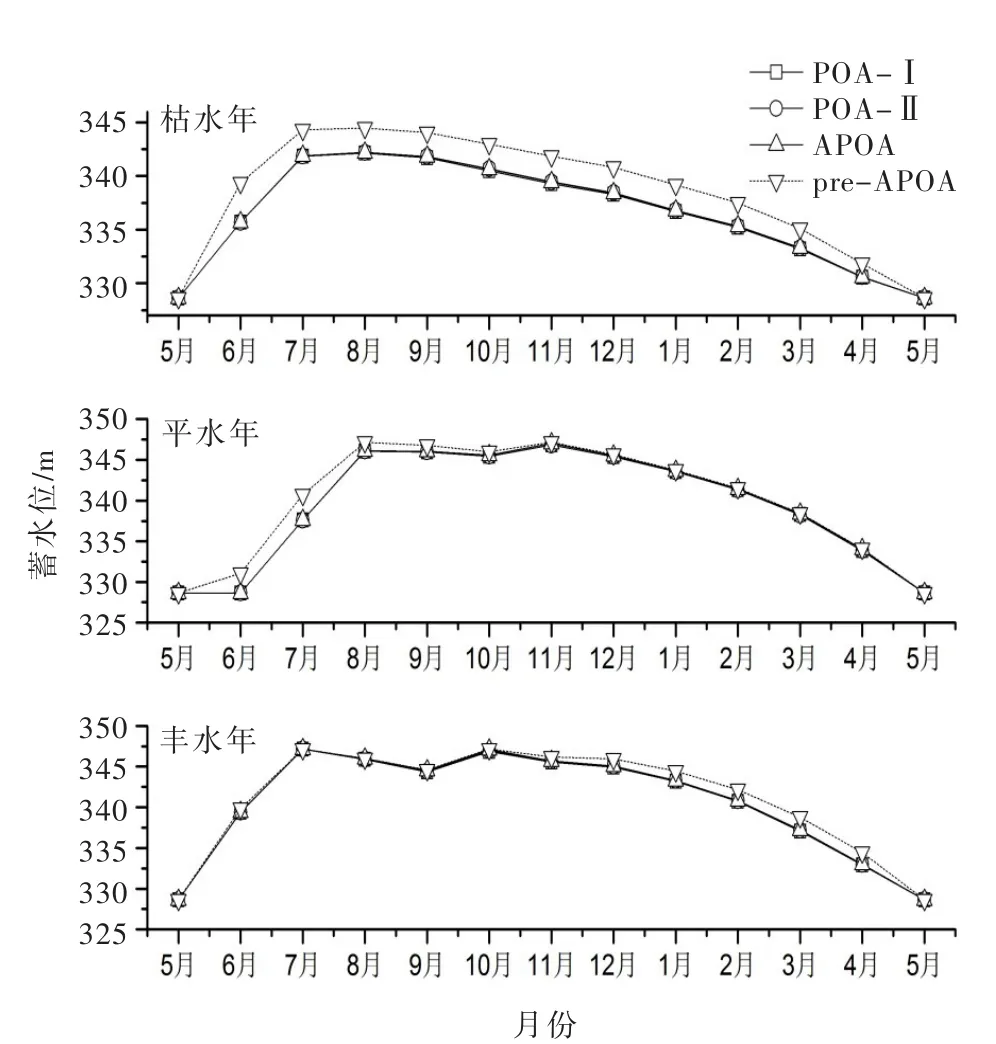
图6 狮子滩水库各典型年优化调度蓄水过程线

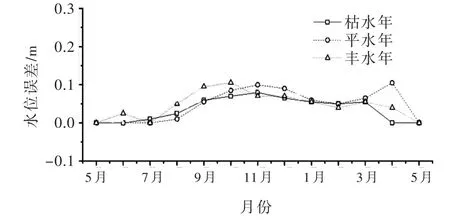
图7 各典型年APOA和POA-Ⅰ的水位相差过程线

5.2 长系列优化计算为了检验本文方法的高效性，对狮子滩水库1958—2005年逐月径流进行长系列优化计算（式（11）的最小出力为保证出力），相关统计指标如表5所示。

由上述计算成果可知，APOA法与传统POA算法相比，主要指标误差很小（发电保证率还略有提高），但APOA算法耗时仅为传统POA算法的1/20。由此表明，解析函数模型及APOA算法在保证不降低计算精度的前提下，能显著减小优化计算时间。

表4 不同算法典型年发电量（单位：亿kW·h）

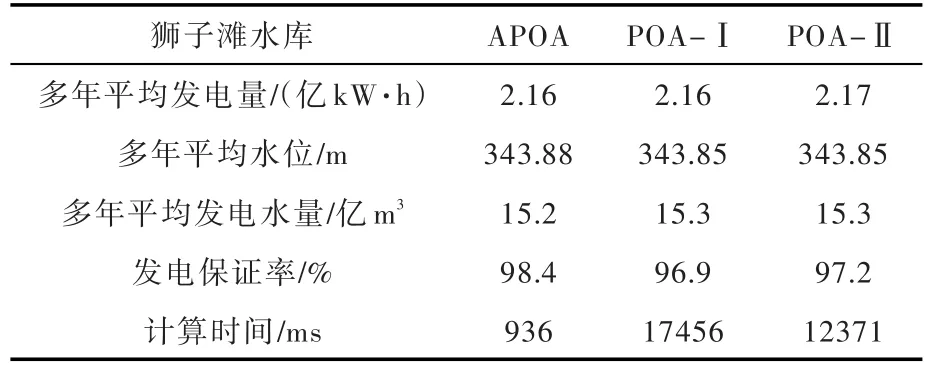
表5 狮子滩水库中长期优化调度计算结果

6 结论

本文针对现行水库发电优化调度数学模型一直采用数值计算方法的缺陷，基于库容-水位关系和尾水流量-水位关系的函数化，建立了水库中长期发电优化调度的解析函数模型，并借鉴传统POA算法提出了解析函数模型的APOA算法。通过狮子滩水库典型年和长系列应用、并与POA算法对比表明，该解析优化数学模型及APOA算法在不降低计算精度的前提下，能显著减小水库优化调度的计算时间。因此，该解析函数模型及APOA算法不仅具有算法稳定、计算效率极高的特点，而且为水库中长期发电优化调度的解析研究途径进行了有益的探索。

［1］赵铜铁钢，雷晓辉，蒋云钟，等.水库调度决策单调性与动态规划算法改进［J］.水利学报，2012，43（4）：414-421.

［2］TOLSON B A，SHOEMAKER C A.Dynamically dimensioned search algorithm for computationally efficient water⁃shed model calibration［J］.Water Resources Research，2007，43（1）：208-214.

［3］ZHANG Z，ZHANG S，WANG Y，et al.Use of parallel deterministic dynamic programming and hierarchical adaptive genetic algorithm for reservoir operation optimization［J］.Computers&Industrial Engineering，2013，65（2）：310-321.

［4］纪昌明，李传刚，刘晓勇，等.基于泛函分析思想的动态规划算法及其在水库调度中的应用研究［J］.水利学报，2016，47（1）：1-9.

［5］孙平，王丽萍，蒋志强，等 .两种多维动态规划算法在梯级水库优化调度中的应用［J］.水利学报，2014，45（11）：1327-1335.

［6］XU B，ZHONG P，ZAMBON R C，et al.Scenario tree reduction in stochastic programming with recourse for hy⁃dropower operations［J］.Water Resources Research，2015，51（8）：6359-6380.

［7］HOWSON H R，SANCHO N G F.A new algorithm for the solution of multi-state dynamic programming problems［J］.Mathematical Programming，1975，8（1）：104-116.

［8］李玮，郭生练，郭富强，等.水电站水库群防洪补偿联合调度模型研究及应用［J］.水利学报，2007，38（7）：826-831.

［9］周佳，马光文，张志刚.基于改进POA算法的雅砻江梯级水电站群中长期优化调度研究［J］.水力发电学报，2010，29（3）：18-22.

［10］程春田，杨凤英，武新宇，等.基于模拟逐次逼近算法的梯级水电站群优化调度图研究［J］.水力发电学报，2010，29（6）：71-77.

［11］程春田，申建建，武新宇.大规模复杂水电优化调度系统的实用化求解策略及方法［J］.水利学报，2012，43（7）：785-795.

［12］冯仲恺，廖胜利，程春田，等 .库群长期优化调度的正交逐步优化算法［J］.水利学报，2014，45（8）：903-911.

［13］张诚，周建中，王超，等.梯级水电站优化调度的变阶段逐步优化算法［J］.水力发电学报，2016，35（4）：12-21.

［14］SCHARDONG A，SIMONOVIC S P.Coupled self-adaptive multi-objective differential evolution and network flow algorithm approach for optimal reservoir operation［J］.Journal of Water Resources Planning&Management，2015，141（10）：04015015.

［15］HADDAD O B，HOSSEINI-MOGHARI S M，LOAICIGA H A.Biogeography-based optimization algorithm for optimal operation of reservoir systems［J］.Journal of Water Resources Planning&Management，2016，142（1）：04015034.