合肥膨胀土地层浅埋双洞地铁隧道施工参数优化研究

陈炜韬， 董宇苍， 方 霖， 于 丽， 舒东利

(1. 中国电建集团成都勘测设计研究院有限公司， 四川 成都 610072； 2. 西南交通大学土木工程学院， 四川 成都 610031； 3. 中国中铁二院工程集团有限责任公司， 四川 成都 610031)

0 引言

合肥市作为华东地区重要的交通枢纽，正处在地铁建设快速发展时期。然而在地铁建设过程中，遇到了如合肥地区膨胀土地层、地铁近接施工对周边结构安全性影响大等众多难题。膨胀土地层具有显著的吸水膨胀、失水收缩的变形特性，在膨胀、收缩变形过程中，能产生较高的膨胀力，如果在隧道施工期间没有采取适当的加固措施，可能会引起围岩膨胀坍塌、隧道底鼓、衬砌开裂等危害[1-2]； 城市地铁施工地质条件本身就极为复杂，加上近接施工容易对围岩造成过度扰动，使围岩状况更为不利[3-4]，若施工不当，极易造成地表沉降过大、隧道结构失稳，甚至会造成坍塌事故[5]。

目前，国内外较多学者已对膨胀土地层、隧道近接施工等问题进行了研究，文献[6-8]研究了膨胀土的膨胀机制，建立了双电层理论与渗透理论； 缪林昌[9]提出了引入饱和度参数的非饱和土弹塑性本构模型; 徐永福[10-11]提出了非饱和膨胀土结构性凝聚力和结构性内摩擦角的概念，并给出了弹塑性本构模型； 晁峰等[12]通过研究特定地区膨胀附加应力场对深基坑土压力的影响，得出在计算深基坑结构时，附加膨胀土压力的量值考虑为34.2 kPa； 毕维红等[13]采用ABAQUS数值软件对深圳轨道交通二期1号线隧道工程进行模拟，研究了开挖右线隧道对左线既有隧道围岩应力分布、地表沉降、隧道衬砌应力变形等的影响； 李斯海[14]采用数值模拟手段对厦门仙岳山双孔小净距隧道施工过程进行研究，得出随着中柱间距减小，围岩稳定性变差，衬砌结构所受荷载增加，结构面临失稳风险的结论。

通过对国内外研究成果调研可知，对膨胀土的研究大多集中于膨胀机制、特性方面，对于膨胀力对隧道结构的影响研究还不全面；近接施工研究重点是对既有隧道结构的影响，并且近接方式也主要为平行、正交方式，而双洞同时施工且近接方式为间距渐变的施工研究较少。因此，本文以合肥市轨道交通1号线为背景，采用热力场-应力场耦合数值模拟方法，对双洞隧道合理净距、双洞隧道掌子面合理距离等施工参数进行优化研究，给出合理的浅埋暗挖双洞地铁隧道施工参数。

1 工程背景

合肥市轨道交通1号线二期工程土建9标段线路位于合肥市肥西县境内，采用浅埋暗挖法施工，暗挖区间全长143 m，线路在暗挖区间里程46 m处由单洞隧道分为双洞隧道，两隧道间距由3.57 m逐渐变为14 m。暗挖区间线路示意图如图1所示。

暗挖区间主要穿越地层岩性为连续分布的黏土，含氧化铁、少量铁锰结核及灰白色高岭土，断面粗糙，干强度高。根据室内试验，得到膨胀土地层物理参数，见表1。暗挖区间膨胀土地层地表裂隙如图2所示。

图1 暗挖区间线路图

地层膨胀潜势自由膨胀率/%重度/(kN/m3)泊松比弹性模量/MPa黏聚力/kPa摩擦角/(°)黏土弱53.820.000.2112.0076.0816.37

(a) 膨胀土地层

(b) 裂缝开展

地铁隧道开挖直径为6.4 m，初期支护采用超前小导管、喷射混凝土、格栅钢架措施，二次衬砌厚度为0.3 m，采用C35混凝土。隧道断面如图3所示。

2 膨胀土附加膨胀应力场模拟方法

本文从膨胀岩吸水膨胀、失水收缩的宏观特性入手，认为这一过程类似于材料热胀冷缩温度效应，采用FLAC3D数值软件中的热力场-应力场耦合方法来实现这一变化过程。

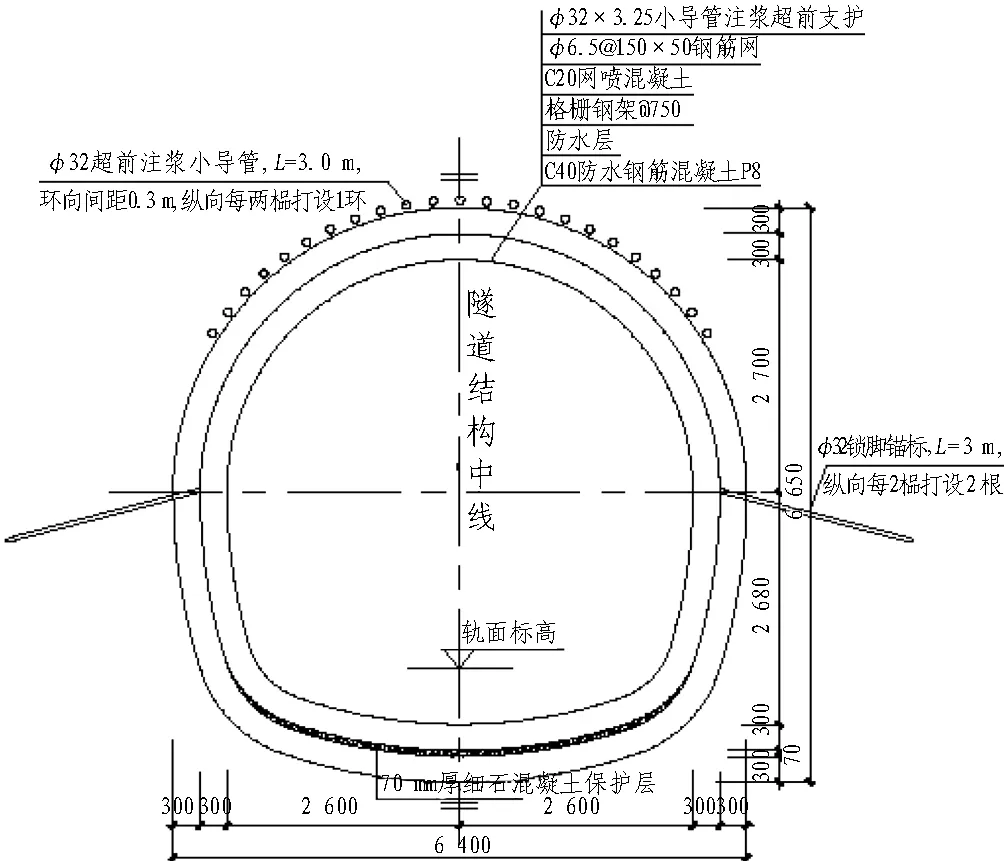
图3 单洞隧道断面图(单位： mm)

2.1 理论基础

FLAC3D数值计算软件中的热力场-应力场耦合是通过重新形成增量应力应变关系来实现的，即从总应变增量中减去由于温度变化产生的应变增量。由于各向同性材料中自由热膨胀只产生均匀的体应变，而不产生角度变形，因此剪应变增量不受影响。热应变增量与温度增量的关系如下：

Δεij=λtΔTσij。

(1)

式中： Δεij为应变分量变化量，i、j=1，2，3；λt为线性热膨胀系数； ΔT为温度变化量;σij为应力分量，i、j=1，2，3。

因此，弹性材料的本构关系为：

(2)

式中：εij为正应变分量，εii为切应变分量，i、j=1，2，3；t为时间变量;α1为比奥系数；Fi为体积力；K、G分别为体积模量和剪切模量。

假设膨胀土是各向同性线性膨胀的，膨胀土的应力场平衡微分方程为：

(3)

式中：xj为x轴方向上的坐标；ρ为岩体密度；E为岩体弹性模量；α为线膨胀系数；W为含水率；ν为泊松比。

2.2 膨胀土热膨胀系数标定

根据暗挖区间的现场测试结果可知，暗挖区间膨胀土自由膨胀力为60 kPa。建立1 m×1 m×1 m单元体模型，在计算模型顶部施加60 kPa膨胀力，通过不断调整热力学模块中的热膨胀系数，使模型表面位移最终为0，从而得出等效热膨胀系数。单元体模型如图4所示，反演结果见表2。

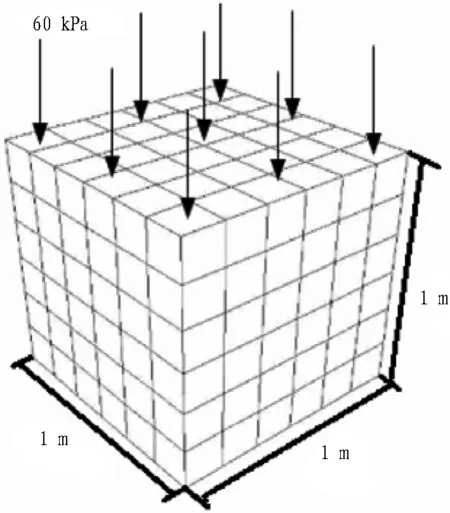
(a) 模型加载

(b) 竖向位移应力图

Table 2 Back calculation results of equivalent thermal expansion coefficient

计算次数膨胀系数β模型顶面位移/mm膨胀率/%13.0×10-51.340.13422.7×10-50.0150.001532.2×10-5-0.420.04242.0×10-5-0.860.086

经过反演分析，当等效热膨胀系数β=2.7×10-5时，模型顶面位移为0.015 mm，其膨胀率只有0.001 5%。因此，暗挖区间膨胀土等效热膨胀系数β=2.7×10-5。

2.3 模型验证

采用热力场-应力场耦合模拟方法，模拟膨胀土地层条件下的隧道开挖过程，并绘制出地表沉降曲线，与暗挖区间实测地表沉降曲线进行对比，以此来验证模型的准确性、合理性。

根据隧道断面形式建立计算模型，覆土厚度为6 m，隧道跨度为6.4 m，高6.65 m。模型上部至地表、仰拱底至隧道下边界各取10.2 m； 以隧道中轴线为原点，计算模型左右边界各取25.5 m，计算模型宽51 m，长67 m，高22.8 m。计算模型如图5所示，隧道结构从图3取值，土层参数从表1取值。

(a) 模型建模

(b) 膨胀力

提取膨胀土地层模拟工况下地表沉降计算结果，并结合现场实测的地表沉降数据，绘制地表沉降曲线对比图，如图6所示。由图6可知： 距离隧道中心10 m范围内，膨胀土地层工况下的地表沉降值和实测的地表沉降值高度吻合； 在距隧道中心10 m范围外，有一定的偏差，最大偏差值为2.47 mm，偏差量较小。通过对比，得出计算模型地表沉降曲线与现场实测地表沉降曲线较为吻合，由此说明此数值模拟计算方法能够准确模拟膨胀土地层暗挖隧道施工过程。

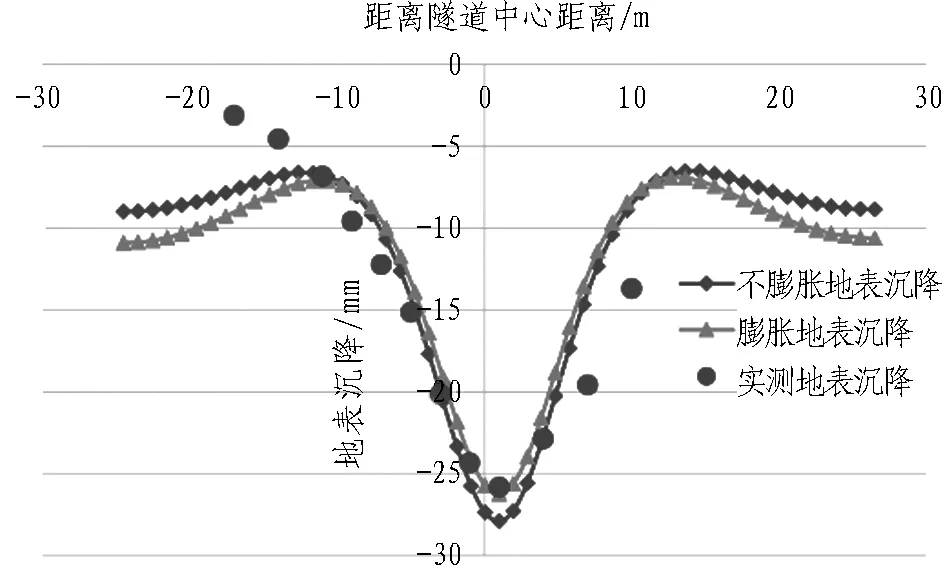
图6 地表沉降对比曲线

3 膨胀土浅埋双洞隧道合理净距分析

3.1 模拟工况及计算模型

由于合肥地铁1号线浅埋暗挖区间两隧道净距由3.57 m渐变为14 m，根据净距变化过程，以洞跨B为单位，采用膨胀力计算模型对8种工况进行模拟计算，如表3所示。由于计算模型较多且相似，因此仅给出净距为0.5B、1.0B的计算模型示意图，其余不再列出。计算模型如图7所示。

表3 不同净距模拟工况表

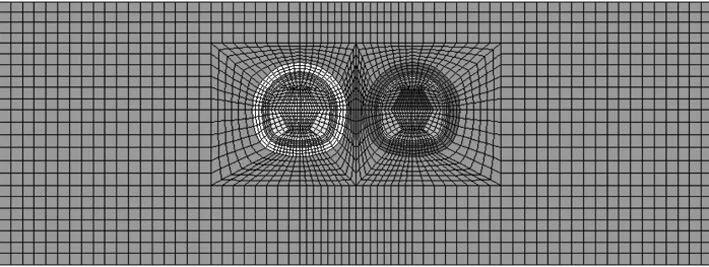
(a) 模型整体图

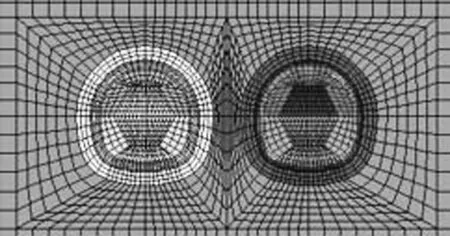
(b) 净距0.5B局部模型

(c) 净距1.0B局部模型

左、右隧道结构各设置3个位移监测点、3个应力监测点，模型上表面以3 m间距布置监测点，监测地表沉降变化规律。隧道结构监测点布置如图8所示。

3.2 不同净距地表沉降结果分析

分别提取不同净距下隧道开挖引起的地表沉降结果，将各工况数据综合绘制成图，如图9所示。各工况地表沉降最大值见表4。

分析图9可知： 当两隧道净距小于1.0B时，地表最大沉降位置出现在距离左线隧道中心10 m位置，且地表沉降曲线呈“V”字型；当两隧道净距大于1.0B时，地表最大沉降量出现位置在距离左线隧道中心23 m位置，且地表沉降曲线呈“W”字型。

(a) 左线隧道

(b) 右线隧道

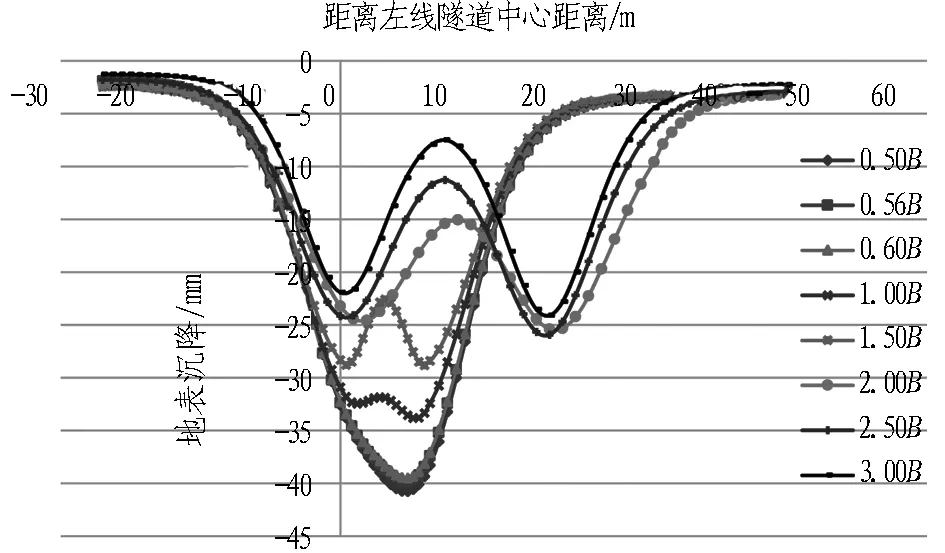
图9 不同净距隧道地表沉降对比图

Fig. 9 Comparison of ground surface settlement curves of tunnels with different clear distances

表4不同工况下最大地表沉降值

Table 4 Maximum ground surface settlements under different conditions

模拟工况最大地表沉降/mm规范限制值/mm是否超限141.2330.00超过240.5830.00超过339.8830.00超过433.8430.00超过528.8230.00不超过625.2630.00不超过725.7630.00不超过824.1230.00不超过

由表4可知，净距在小于1.5B时的各工况最大地表沉降均大于规范值要求。因此，若仅考虑地表沉降因素，两隧道净距应大于1.5倍洞径。

3.3 衬砌内力结果分析

根据隧道衬砌内力计算结果绘制内力增量图，如图10所示。由图10分析可知，净距对结构弯矩影响规律为： 随着净距的增加，结构弯矩增量总体呈减小趋势，净距的影响范围为0～3倍洞径；在0.5B～1B净距内，衬砌结构各监测点弯矩增量急剧降低，在净距为1B时，各监测点弯矩增量值为10%左右；在1B～2B净距内，衬砌结构弯矩增量呈先增加后降低的变化趋势； 当净距大于3B时，隧道结构弯矩增量基本为0。净距对结构轴力的影响规律为：在0.5B～2B净距内，隧道结构拱顶、左边墙处的轴力增量线性减小至0，而右边墙轴力增量急剧减小至0；在净距大于2B后，隧道结构轴力增量几乎为0。

(a) 弯矩增量

(b) 轴力增量

Fig. 10 Internal force increments of tunnel lining with different clear distances

通过分别分析净距对结构弯矩、轴力影响规律可知，若仅考虑衬砌结构受力因素，两隧道净距应大于1.5倍洞径。

3.4 围岩塑性区结果分析

不同净距工况下围岩塑性区分布如图11所示。可以看出净距小于1.0B时，围岩塑性区贯通，中间岩柱破坏; 隧道净距大于1.0B时,围岩塑性区不贯通，中间岩柱不发生塑性破坏。

(a) 净距0.50B(b) 净距0.56B(c) 净距0.60B(d) 净距1B

(e) 净距1.5B(f) 净距2.0B(g) 净距2.5B(h) 净距3.0B

图11不同净距围岩塑性区分布

Fig. 11 Plastic zone distributions of surrounding rock of tunnel with different clear distances

综合上述分析可知，若考虑隧道开挖时地表沉降因素，两隧道净距应大于1.5倍洞径；若考虑衬砌结构受力因素，两隧道净距应大于1.5倍洞径；若考虑开挖围岩塑性分布因素，两隧道净距应大于1.0倍洞径。因此，建议两隧道净距应大于1.5倍洞径。

4 双洞隧道掌子面合理距离分析

为了减少隧道施工工期，在开挖左线隧道时可以同时开挖右线隧道，但两隧道的掌子面必须保持一定距离才能保证施工的安全性，且二次衬砌也要及时跟进，以减小后行洞对先行洞的影响。

4.1 模拟工况及计算模型

计算参数取值与前一节相同，建立附加膨胀应力场下的两隧道渐变间距模型，模型纵向取60 m，长71 m，宽23 m，如图12所示。

(a) 整体网格图

(b) 衬砌网格图

通过选取固定断面作为监测断面的方式，排除由于双洞隧道净距的变化对计算结果的影响。选取距离隧道洞口20 m处的断面为监测断面，分析不同掌子面间距下，隧道开挖通过此断面时地表位移及拱顶位移的变化,监测断面如图13所示。分别分析不同掌子面距离对围岩、隧道结构的影响，以确定合理的掌子面距离。计算模型工况见表5。

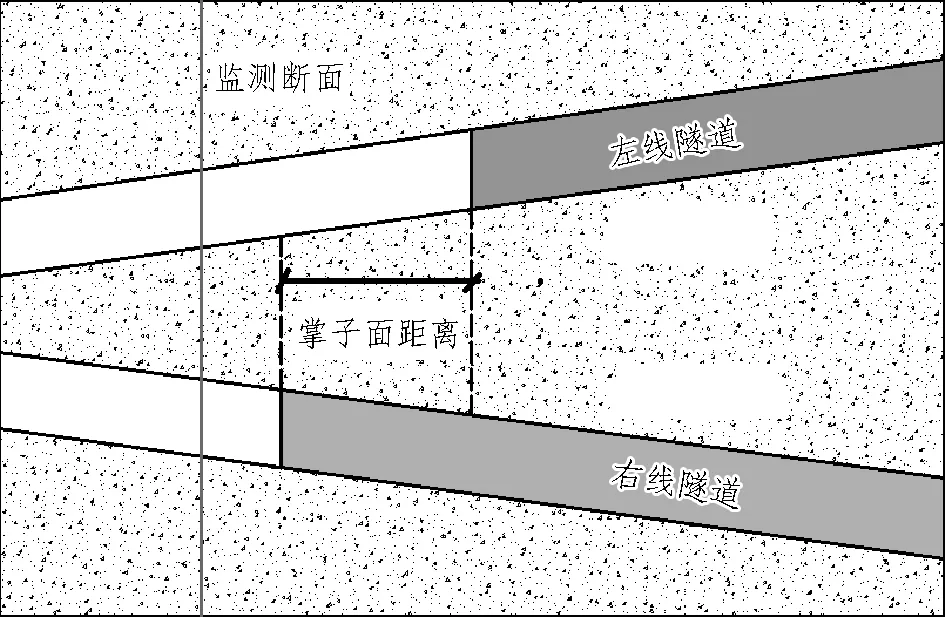
图13 监测断面

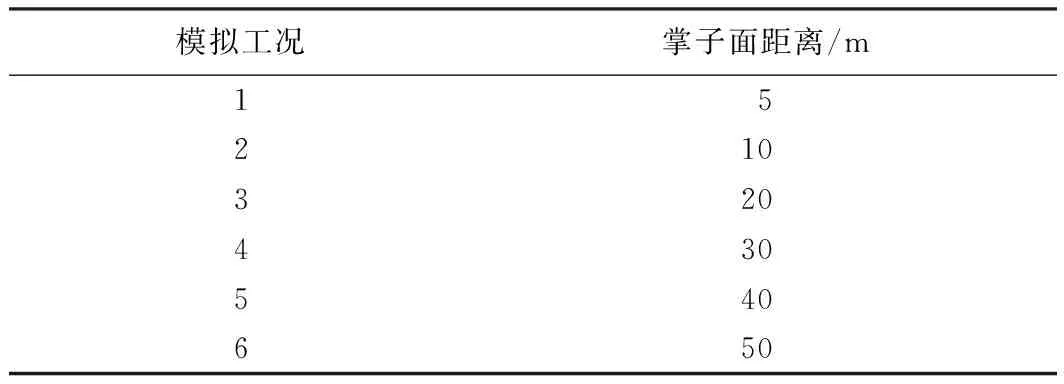
模拟工况掌子面距离/m15210320430540650

4.2 不同掌子面距离下地表沉降结果分析

分析不同掌子面距离下横向、纵向地表沉降规律，计算结果如图14所示。由图14分析可知： 从单洞开挖地表沉降分析，横向地表沉降呈“V”字型分布，单洞开挖50 m后最大地表沉降为25 mm，单洞开挖现场实测最大地表沉降为26.8 mm，两者数据较为吻合； 随着两隧道掌子面距离增大，隧道间相互影响越来越小，其横向及纵向地表沉降最大值也越来越小； 两掌子面距离小于40 m时，横向、纵向地表沉降最大值都大于30 mm，已经超出了地表沉降的规范限制值； 两掌子面距离大于40 m时，左右洞开挖的影响相对较小，地表沉降最大值小于规范限制值。因此，若仅考虑地表沉降因素，两掌子面距离应大于40 m。

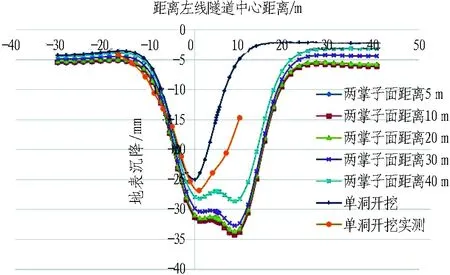
(a) 横向地表沉降

(b) 纵向地表沉降

Fig. 14 Horizontal and vertical ground surface settlement rules of tunnel with different distances between two tunnels

4.3 不同掌子面距离下拱顶沉降结果分析

不同掌子面距离开挖的拱顶沉降数值如图15所示。

图15 不同掌子面距离拱顶纵向沉降曲线

Fig. 15 Longitudinal settlement curves of crown top of tunnel with different distances between two tunnels

由图15可知： 掌子面距离为5 m时，引起的左洞拱顶沉降增量达到了30.99%，对隧道的位移影响较大； 而掌子面距离为40 m时，沉降增量降低到 7.25%，对隧道的影响相对较小。因此，若仅考虑拱顶沉降因素，若以增量10%作为控制标准，两掌子面距离应大于40 m。

4.4 不同掌子面距离下围岩塑性区结果分析

不同掌子面距离围岩塑性区分布如图16所示。由图16可知： 随着两隧道掌子面距离增加，两隧道中间区域围岩塑性区贯通范围逐渐减小； 当两掌子面距离小于30 m时，两隧道中间围岩塑性区贯通；当两掌子面距离大于30 m时，围岩塑性区不贯通。因此，若仅考虑围岩塑性区分布因素，两隧道掌子面距离应大于30 m。

(a) 5 m (b) 10 m (c) 20 m (d) 30 m (e) 40 m

图16不同掌子面距离围岩塑性区分布图

Fig. 16 Plastic zone distributions of surrounding rock of tunnel with different distances between two tunnels

综合上述分析可知，若考虑隧道开挖时地表沉降因素，两掌子面距离应大于40 m；若考虑隧道拱顶沉降因素，两掌子面距离应大于40 m；若考虑两隧道中间围岩塑性区分布因素，两掌子面距离应大于30 m。因此，建议两掌子面距离应大于40 m。

5 结论与建议

本文以合肥市轨道交通1号线为背景，采用热力场-结构场耦合数值模拟方法，对浅埋双洞地铁隧道合理净距、双洞掌子面合理距离施工参数进行优化研究，主要结论如下。

1)采用热力场-应力场耦合数值模拟方法来模拟膨胀土吸水膨胀、失水收缩的宏观特性对隧道结构的影响作用，将数值模拟结果与现场实测值对比，验证了该方法的正确性、合理性。

2)当两隧道净距大于1.5倍洞径时，最大地表沉降值为28.82 mm，衬砌结构内力增量小于20%，双洞中柱塑性区不贯通。建议双洞隧道间距大于1.5倍洞径。

3)当两隧道掌子面距离大于40 m时，地表沉降小于30 mm，拱顶沉降增量为7.25%，两隧道中柱塑性区不贯通。建议两隧道掌子面距离大于40 m。

本文主要通过全地层设置等效膨胀系数，以实现膨胀作用模拟过程，但尚未研究应力场对膨胀率的影响，今后可以进一步深入研究。

[1] 陈鸿， 汪大新. 膨胀土隧道仰拱施工技术[J]. 隧道建设, 2010, 30(5): 582.

CHEN Hong, WANG Daxin. Construction technology for tunnel invert in swelling soil[J]. Tunnel Construction, 2010, 30(5): 582.

[2] 贾彦斌. 膨胀土地区路基施工技术[J]. 隧道建设, 2006, 26(1): 85.

JIA Yanbin. Construction technology of roadbed in swelling soil area[J]. Tunnel Construction, 2006, 26(1): 85.

[3] 骆建军, 张顶立, 王梦恕, 等. 地铁施工沉降监测分析与控制[J]. 隧道建设, 2006, 26(1): 10.

LUO Jianjun, ZHANG Dingli, WANG Mengshu, et al. Analysis and control of settlement in metro construction[J].Tunnel Construction, 2006, 26(1): 10.

[4] 刘淼. 西安地铁侧坡出入段线上跨既有隧道施工影响分析[J]. 隧道建设, 2016, 36(7): 826.

LIU Miao, Analysis of influence of construction of access section of Xi′an Metro on existing shield tunnels[J].Tunnel Construction, 2016, 36(7): 826.

[5] 崔玖江. 盾构隧道施工风险与规避对策[J]. 隧道建设, 2009, 29(4): 377.

CUI Jiujiang. Risk and countermeasures for construction of shield-bored tunnels[J]. Tunnel Construction, 2009, 29(4): 377.

[6] INGLES O G. Soil chemistry relevant to the engineering behavior of soils[M]. Sydney: Butterworths, 1968.

[7] LOUGHNAN F C. Chemical weathering of the silicate minerals[M]. New York: Elsevier, 1969.

[8] MITCHELL J K, SOGA Kenichi. Fundmentals of soil behavior[M]. New York： Wiley, 2005.

[9] 缪林昌. 非饱和土的本构模型研究[J]. 岩土力学， 2007, 28(5): 855.

MIAO Linchang. Research of constitutive model of unsaturated soils[J]. Rock and Soil Mechanics, 2007, 28(5)： 855.

[10] 徐永福. 非饱和膨胀土结构性强度的研究[J]. 河海大学学报， 1999, 27(2): 86.

XU Yongfu. Structural strength of unsaturated expansive soils[J]. Journal of Hohai University, 1999, 27(2): 86.

[11] 徐永福. 膨胀土地基承载力研究[J]. 岩石力学与工程学报， 2000, 19(3): 387.

XU Yongfu. Study of bearing capacity of expansive soil basement[J].Chinese Journal of Rock Mechanics and Engineering, 2000, 19(3): 387.

[12] 晁峰, 王明年, 舒东利, 等. 膨胀土附加应力场对深基坑土压力的影响[J]. 中南大学学报(自然科学版), 2016, 47(9): 3177.

CHAO Feng, WANG Mingnian, SHU Dongli, et al. Earth pressure of deep foundation pit effected by additional stress field of expansive soil[J]. Journal of Central South University(Science and Technology), 2016, 47(9): 3177.

[13] 毕维红, 江志峰, 常斌. 近距离地铁施工的有限元数值模拟[J]. 岩土力学, 2005, 26(2): 277.

BI Weihong, JIANG Zhifeng, CHANG Bin. Numerical simulation for constructions of metro tunnels with short distance between them[J]. Rock and Soil Mechanics, 2005, 26(2): 277.

[14] 李斯海. 厦门市仙岳山隧道围岩稳定性三维有限元计算分析[J]. 岩石力学与工程学报, 2000, 19(2): 211.

LI Sihai. 3D FEM analyses of stability of Xianyueshan Tunnel of Xiamen[J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(2): 211.