兴延高速浇花峪隧道爆破振动测试分析研究

江雅勤， 刘殿书, *， 武 宇， 谢 烽， 袁 达， 张会歌

(1. 中国矿业大学(北京)力学与建筑工程学院， 北京 100083； 2. 北方爆破科技有限公司， 北京 100089)

0 引言

目前国内隧道掘进仍然以钻爆法为主，爆破振动严重影响了隧道的施工安全及施工效率，会对衬砌及围岩造成严重的损伤，影响结构的稳定和安全[1-4]。国内关于爆破振动的研究主要集中在振速和主频的衰减规律上。卓效明[5]为了研究不同级别围岩中振速的衰减规律，通过隧道爆破振动测试试验获得了近千个数据，然后分别对隧道纵、横断面及掌子面附近的振速进行了分析，发现平行于掌子面同一断面上边墙处的振速大于拱顶的振速，但也存在少数相反情况。饶增[6]对实测的隧道振动数据进行了分析，利用萨道夫斯基公式对振速拟合，得到了隧道振速的衰减公式。傅洪贤等[7]对隧道爆破近区的围岩进行了振速监测，通过大量的测试数据得出了隧道掌子面后方拱顶、掌子面正上方和侧面围岩的爆破振动规律，平行于掌子面同一断面上拱顶处的质点峰值速度大于拱脚和边墙处的质点峰值速度。陆瑜[8]利用数值模拟手段，以隧道循环进尺为变量，分析了隧道拱顶、拱脚和边墙部位围岩的质点速度，发现随着与掌子面距离的增大，围岩质点的峰值振速先是急剧衰减而后平缓衰减，隧道循环进尺越大对围岩的扰动越严重。文献[9-10]的研究表明，振动信号不同的频带对结构的影响也有所不同，由小波分析法可以清晰地得到振动信号各个频带的信息，能够更好地确定振动对隧道工程结构的影响。

目前关于爆破施工隧道内振动速度及其传播规律的研究成果仍较缺乏，理论体系仍不成熟。因此，采用隧道爆破工程现场振动测试试验研究隧道爆破的振动规律非常有意义。本文结合工程现场实际情况，从信号的不同频带方面研究隧道不同位置的爆破振动，对隧道上台阶爆破掘进过程中初期支护衬砌结构的振动进行监测，得到振速的传播规律、主频大小及能量分布，可为爆破振速预测及初期支护衬砌结构的安全防护提供指导。

1 工程背景

试验依托于北京兴延高速公路浇花峪右线隧道爆破掘进工程，隧道拱顶至地表的距离为24～26 m，为浅埋隧道，区域内地势较平坦。浇花峪隧道采用两台阶掘进爆破施工，单次开挖面尺寸较大，历次爆破总药量均超过200 kg，爆破地震效应明显。为减小爆破施工中的振动，防止隧道结构破坏，隧道上台阶采用掘进爆破，下台阶采用水平孔拉槽爆破。爆破时上、下台阶开挖面相距70 m以上，上台阶开挖高度为7.8 m，开挖面积为90.5 m2，下台阶开挖面积为59.5 m2。上台阶炮孔布置如图1所示。振动测试试验段均为Ⅲ级围岩，爆破参数如表1所示。上台阶爆破掘进过程中，现场试验主要监测里程YK28+190～+354的隧道初期支护衬砌振动情况。

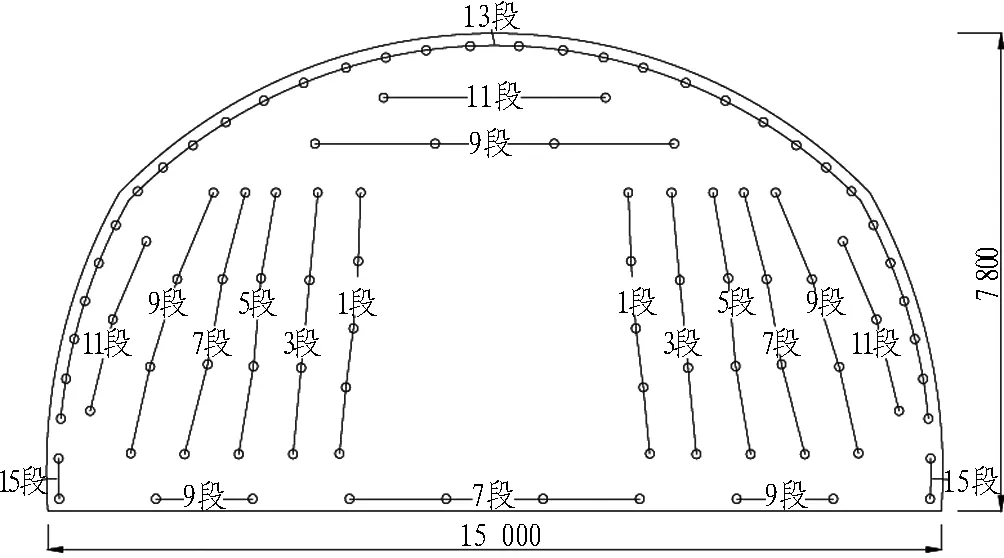
(a) 横剖面图

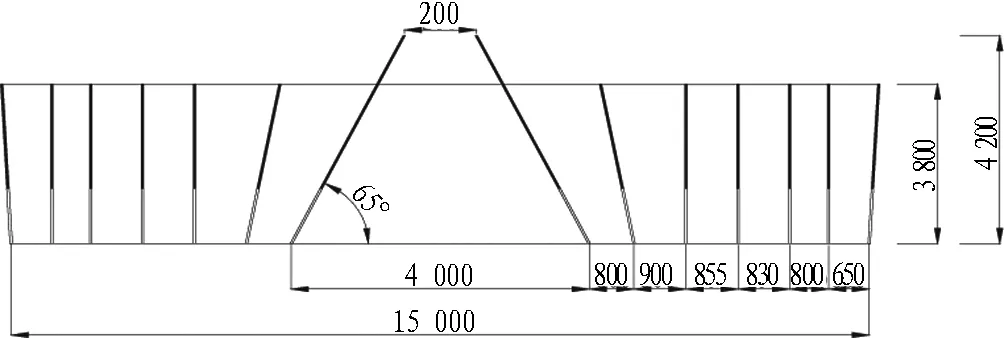
(b) 俯视图

炮孔名称段位炮孔数量孔深/m装药量/kg掏槽孔18～103.2～4 24～38扩槽孔138 3～3.8 18～28.4扩槽孔258 3～3.6 16～26.8崩落孔178 3～3.2 16～24.2崩落孔2982.4～3 16～19.2崩落孔31162.4～314.4～16.8崩落孔4942.2～2.89.6～12崩落孔51122.2～2.8 4～6周边孔13261.8～2 22～28底板孔1743.2～3.69.6～12底板孔2943.2～3.69.6～12底板孔3158 4～514.4～19.2

2 试验方案

选取距离掌子面38 m处的隧道断面作为首次测试断面。为研究隧道钻爆施工时拱形结构的振动效应，在测试断面拱顶、拱腰和边墙处各布置1个测点，采集爆破掘进时测点的的振动数据。测点布置如图2所示。

在布置测点时，为了保证整个测试过程不出现仪器脱落的情况，分别在拱顶、拱腰和边墙处进行钻孔，并采用固定卡将传感器固定在待测位置，然后采用锚固剂使待测位置平整并加强固定效果，最终使传感器与隧道初期支护衬砌刚性连接，传感器布置方式如图3所示。

图2 测点布置图

图3 传感器布置方式示意图

3 试验结果分析

3.1 振动规律分析

在隧道拱顶、拱腰和边墙测点处共测得69组有效数据，对69组数据进行回归分析。表2仅示出了隧道拱顶、拱腰和边墙测点处的部分测试数据。

利用萨道夫斯基公式对隧道拱顶、拱腰及边墙处垂直方向、水平切向及水平径向的振速与比例距离的关系进行拟合，拟合得到的振速样本和回归曲线如图4所示。

由图4可以看出，无论在哪个方向上，总有振速v拱顶>v拱腰>v边墙，且随着比例距离的增加，3个方向的振速逐渐接近，当比例距离增加至一定数值时，3个方向的振速可能会重合。

为了研究隧道爆破过程中不同方向上地震波的衰减规律，采用萨道夫斯基公式对测试数据进行回归，回归后的K、α分别如表3和表4所示。

由表3可知： 隧道拱顶垂直方向、水平切向和水平径向振速的K值均大于其他测试位置相应方向振速的K值。在相同条件下，拱顶的振速最大，且其垂直方向振速较水平切向和水平径向振速大； 随着传播路径的延长振动波逐渐衰减，与其他测试位置相比，拱顶的爆破剩余能量最大。由表4可知： 拱顶垂直方向、水平切向和水平径向的α绝对值均大于其他测试位置相应方向的α绝对值，说明拱顶振速衰减最快，且其垂直方向振速比其他2个方向的振速衰减快。

表2 隧道拱顶、拱腰和边墙测点部分测试数据

(a) 拱顶

(b) 拱腰

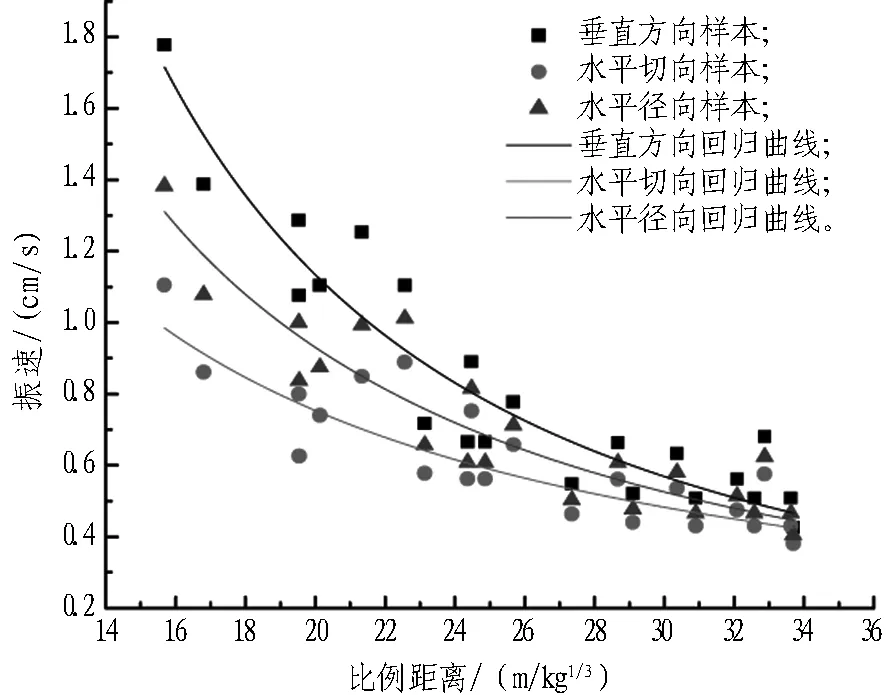
(c) 边墙

Fig. 4 Vibration velocity samples and regression curves of tunnel crown top, hance and sidewall

表3 测试位置3个方向的K值

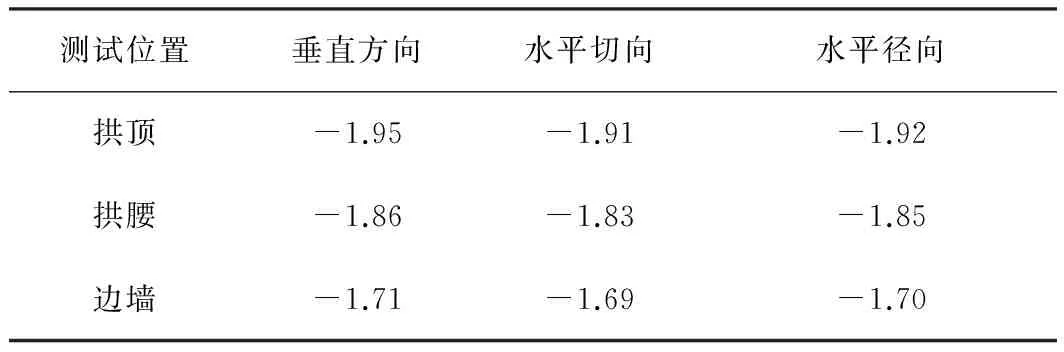
表4 测试位置3个方向的α值

3.2 主频分析

将隧道爆破振动测试中获得的94组地面振动波形作为样本，隧道拱顶、拱腰和边墙垂直方向部分振动主频如表5所示。

表5隧道拱顶、拱腰和边墙垂直方向振动主频

Table 5 Basic vibration frequency of tunnel crown top, hance and sidewall along vertical direction

测点编号爆心距R/m总装药量Q/kg比例距离/(m/kg1/3)拱顶主频/Hz拱腰主频/Hz边墙主频/Hz1382226.2852.2658.7971.8526322210.433.1037.2445.5239222215.1934.3938.6947.294422186.9853.9460.6874.165522188.6469.3978.0795.416451797.2688.2999.32121.407551798.8881.4791.66112.0287017911.327.4330.8637.7299917915.9814.7416.5820.26

利用主频回归分析方法[11]分别对拱顶、拱腰以及边墙处的爆破振动主频进行回归，隧道拱顶、拱腰和边墙处垂直方向振动主频回归曲线如图5所示。

由图5主频回归曲线可知，隧道围岩不同位置处的振动主频存在差异，大小关系为：f拱顶>f边墙>f拱腰。从隧道围岩各位置处的振速分布规律可知，随着测点与爆源距离的增加，各个位置的振速差异不大，在振速相同或者接近时，拱腰位置的主频最低。因此，从振速-主频的安全判据来看，拱腰位置出现破坏情况的风险最大。

3.3 振动信号的小波分析

3.3.1 频带分析

选取药量为222 kg时距离掌子面67 m处拱顶、拱腰和边墙(分别记为sd、sy和sb)的振动波形进行分析[12-13]。爆破参数如表6所示。

(a) 拱顶

(b) 拱腰

(c) 边墙

f为主频，Hz。

图5隧道拱顶、拱腰和边墙处垂直方向振动主频回归曲线

Fig. 5 Regression curves of basic vibration frequency of tunnel crown top, hance and sidewall along vertical direction

信号的采样频率设置为2 000 Hz，则其奈奎斯特频率为1 000 Hz[14]。因此，采用sym5小波基将信号进行9层分解，共10个频带，即D1(500～1 000 Hz)、D2、D3、D4、D5、D6、D7、D8、D9和A9，其是由高频到低频进行排列的，然后重构不同频带的分解系数。sd信号的小波分解和重构如图6所示，可以直观地了解sym5小波基的分解效果。

表6 距离掌子面67 m处的爆破参数

经小波分解后的信号，高频分量为D1—D9，低频分量为A9。D1为信号分解出的9个分量中频率最高的部分，峰值振速为0.172 29 cm/s，而原始波形的峰值振速为0.956 1 cm/s，说明拱顶振动的高频部分能量占比很大。D2、D3和D4信号频率较低，振速较大，其中D4信号的振速最大，且接近于原始信号的最大振速，达到了0.967 cm/s。参照小波分解每个波段的频带，D4为振动信号的优势频段，能量占比最大，在同等条件下，拱腰和边墙D4频带的振速小于拱顶的振速。A9的频率最低，但是其峰值振速小，即所携带的能量也很小，虽然持续时间较长，但是不会对隧道结构造成危害。

对sy、sb信号进行小波分解后发现，位置不同，优势频带也在发生变化。拱顶振动的优势频带集中在中高频区域，边墙振动的优势频带集中在中低频区域，拱腰振动的优势频带集中在低频区域。当优势频带向A9靠拢时，频带主频接近于结构自振频率，且耦合性越好，引起的振动越强烈，对隧道结构的危害也越大。

3.3.2 小波能量分析

爆破地震波的产生、传播以及对隧道结构的影响过程，本质是能量在传播介质中传递和转移的过程。不同频带振动分量的振动强度直接由其相应小波频带能量的大小反映，由此可获取不同频带振动分量下结构的响应特性。各频带的能量及能量占比可根据文献[15]中的公式计算。

分别对距掌子面67 m处的sd、sy和sb 3个振动信号进行小波分解，然后绘出各频带的能量占比。不同位置处各频带的能量分布情况如图7所示，隧道不同位置各频带的能量占比如表7所示。

(a) 重构信号 (b) 原始信号

(c) 重构信号误差 (d) 重构信号D1

(e) 重构信号D2 (f) 重构信号D3

(g) 重构信号D4 (h) 重构信号D5

(i) 重构信号D6 (j) 重构信号D7

(k) 重构信号D8 (l) 重构信号D9

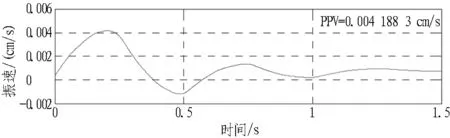
(m) 重构信号A9

PPV为质点峰值振速。

图6 sd信号的小波分解和重构

Fig. 6 Wavelet decomposition and reconstruction of sd signal

(a) sd信号

(b) sy信号

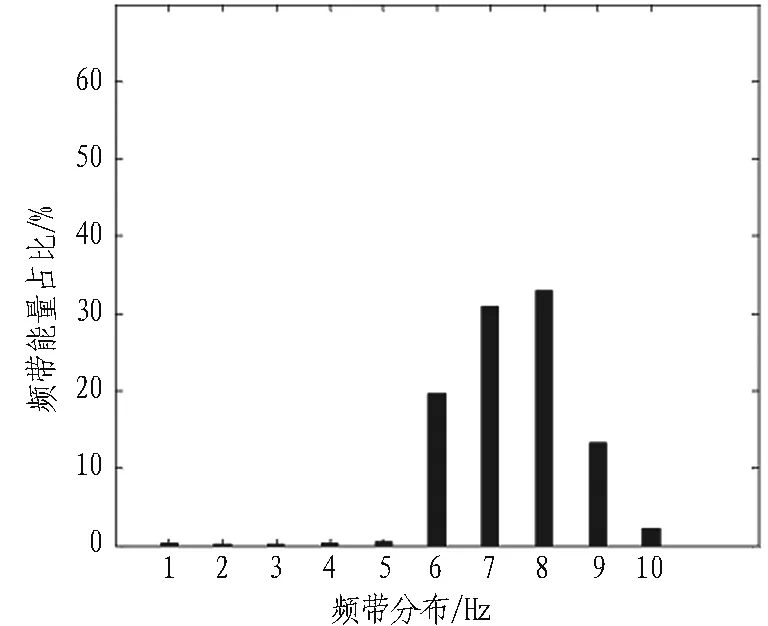
(c) sb信号

Fig. 7 Energy distributions of every bandwidth in different positions of tunnel

表7隧道不同位置各频带的能量占比

Table 7 Energy proportions of every bandwidth in different positions of tunnel

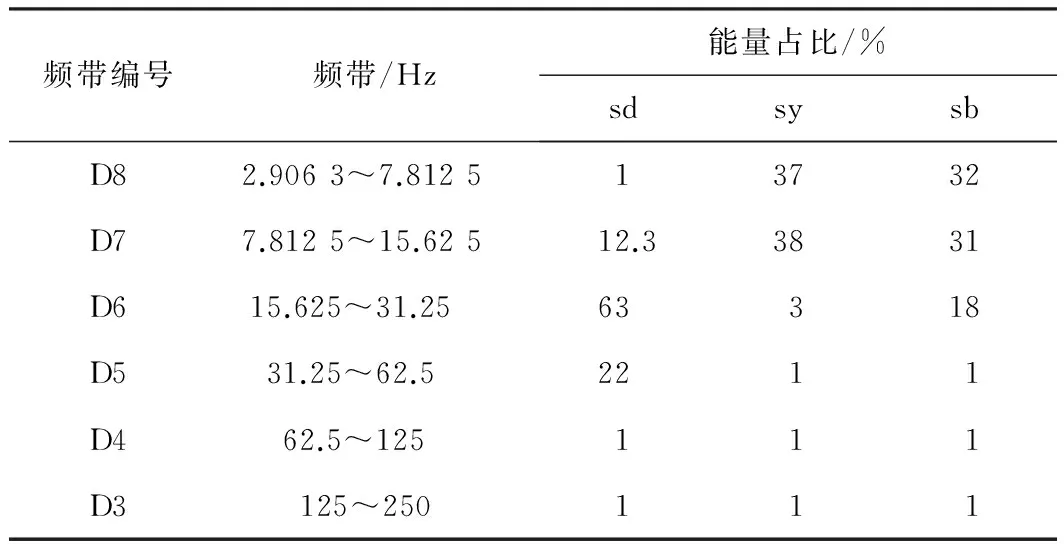
频带编号频带/Hz能量占比/%sdsysbD82.9063～7.812513732D77.8125～15.62512.33831D615.625～31.2563318D531.25～62.52211D4 62.5～125111D3 125～250111

通过上述计算可知，3～200 Hz频段集中了爆破振动信号的大部分优势能量，能量最大值一般出现在主频率所在的频带，高频部分的能量占比不大。由拱顶、拱腰和边墙处的能量分布可知，拱顶处的频率成分相对单一，频带宽度较小，而拱腰和边墙处的频率成分相对较丰富，频带宽度较大。其中，拱腰和边墙处的低频成分能量占比要远高于拱顶，且拱腰位置的低频能量最高，在振速接近或相同时，拱腰发生破坏的风险最大。

4 结论与讨论

通过对Ⅲ级围岩浅埋隧道爆破过程中拱顶、拱腰和边墙位置的振速进行监测，得到了隧道拱顶、拱腰和边墙位置的振动数据，然后对其振动规律和主频进行了分析，并采用小波分析方法对各频带的特征进行了阐述，得出以下结论。

1)针对振速3个方向的分量，总有v拱顶>v拱腰>v边墙，且随着比例距离的增加，3个方向的振速逐渐接近，说明随着比例距离的增加，测点位置对振速的影响会逐渐减小。

2)由主频回归曲线可知，隧道围岩不同位置处的振动主频存在差异，大小关系为：f拱顶>f边墙>f拱腰。由不同位置处振速的分布规律可知，随着测点与爆源距离的增加，各个位置的振速差异不大，拱腰位置的主频最低，说明拱腰位置发生破坏的风险要大于拱顶和边墙。

3)爆破振动信号的大部分优势能量集中在3～200 Hz频段。由拱顶、拱腰和边墙的能量分布可知，拱腰和边墙处的频率成分相对较丰富，频带宽度较大，拱腰位置的低频能量最高，说明此处发生破坏的风险最大。

由于试验条件的限制，本文测试范围为距离隧道掌子面38～164 m处，对<38 m处隧道爆破近区的振动效应未进行研究。距爆源越近，振动越强烈，爆破地震波的时频特征变化越快，这无论是对试验仪器还是分析方法都提出了更大的挑战，因此，对这一领域进行研究将会很有价值。

[1] 杨佑发, 崔波. 爆破震动速度峰值的预测[J]. 振动与冲击, 2009, 28(10): 195.

YANG Youfa, CUI Bo. Prediction for vibration intensity due to blasting induced ground motions[J]. Journal of Vibration and Shock, 2009, 28(10): 195.

[2] 卢文波, 张乐, 周俊汝, 等. 爆破振动频率衰减机制和衰减规律的理论分析[J]. 爆破, 2013, 30(2): 1.

LU Wenbo, ZHANG Le, ZHOU Junru, et al. Theoretical analysis of decay mechanism and law of blasting vibration frequency[J]. Blasting, 2013, 30(2): 1.

[3] 张继春, 曹孝君, 郑爽英, 等. 浅埋隧道掘进爆破的地表震动效应试验研究研究[J]. 岩石力学与工程学报, 2005, 24(22): 4158.

ZHANG Jichun, CAO Xiaojun, ZHENG Shuangying, et al. Experimental study of vibration effects of ground due to shallow tunnel blasting[J].Chinese Journal of Rock Mechanics and Engineering, 2005, 24(22): 4158.

[4] 丛树翠, 王海亮. 相邻隧道爆破震动波的传播规律研究[J]. 隧道建设, 2012, 32(4): 502.

CONG Shucui, WANG Hailiang. Study of propagation rules of vibration waves by blasting of adjacent tunnel[J]. Tunnel Construction, 2012, 32(4): 502.

[5] 卓效明. 厦门仙岳山公路隧道爆破振动测试报告[J]. 现代隧道技术， 2002， 39(2): 59.

ZHUO Xiaoming. Test report of vibration induced by blasting in Xianyueshan municipal tunnel in Xiamen[J]. Modern Tunnelling Technology, 2002， 39(2): 59.

[6] 饶增. 隧道钻爆施工对初期支护的影响及控制标准的研究[D]. 北京: 北京交通大学， 2010.

RAO Zeng. The study of impacts and control standard of drilling and blasting method on primary support[D]. Beijing: Beijing Jiaotong University， 2010.

[7] 傅洪贤, 赵勇, 谢晋水, 等． 隧道爆破近区爆破振动测试研究[J]． 岩石力学与工程学报, 2011, 30(2): 335.

FU Hongxian，ZHAO Yong，XIE Jinshui, et al. Study of blasting vibration test of area near tunnel blasting source[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30 (2): 335.

[8] 陆瑜. 公路隧道光面爆破围岩振动衰减规律[J]. 水利与建筑工程学报, 2014, 12(6): 87.

LU Yu. The attenuation law of vibrations in highway tunnel surrounding rocks caused by smooth blasting[J]. Journal of Water Resources and Architectural Engineering, 2014, 12 (6): 87.

[9] 王恒富, 陈寿如. 基于小波分析的浅埋隧道爆破地震波时频特征研究[J]. 采矿技术, 2014, 14(3): 89.

WANG Hengfu, CHEN Shouru. Study of time-frequency characteristics of blasting seismic wave in shallow tunnel based on wavelet analysis[J]. Mining Technology, 2014, 14(3): 89.

[10] 刘洋, 赵明阶, 贺林林, 等. 石龙山隧道爆破振动信号的小波分析[J]. 重庆交通大学学报(自然科学版), 2012, 31(2): 223.

LIU Yang, ZHAO Mingjie, HE Linlin, et al. Wavelet analysis of blasting seismic signals of Shilongshan Tunnel[J]. Journal of Chongqing Jiaotong University (Natural Science), 2012, 31(2): 223.

[11] 张立国, 龚敏, 于亚伦. 爆破振动频率预测及其回归分析[J]. 辽宁工程技术大学学报， 2005, 24(2): 187.

ZHANG Liguo, GONG Min, YU Yalun. Forecast and regression analysis of blasting vibration frequency[J]. Journal of Liaoning Technical University, 2005, 24(2): 187.

[12] 林秀英， 张志呈. 爆破地震波的频谱分析[J]. 中国矿业， 2000， 6 (9): 77.

LIN Xiuying, ZHANG Zhicheng. Spectrum analysis of seismic wave from blasting[J]. China Mining Magazine, 2000， 6(9): 77.

[13] 范磊， 沈蔚. 爆破振动频谱特性实验研究[J]. 爆破，2001，18(4)： 18.

FAN Lei, SHEN Wei. Experimental study of frequency spectrum characteristics of blast vibration wave[J]. Blasting, 2001, 18(4): 18.

[14] 刘凤钱, 赵明生, 池恩安. 爆破振动与车辆振动信号时频特性对比分析[J]. 爆破, 2010, 27(4): 105.

LIU Fengqian, ZHAO Mingsheng, CHI En′an. Comparative analysis of time-frequency characteristic between blasting vibration and vehicle vibration signals[J]. Blasting, 2010, 27(4): 105.

[15] 林大超, 施惠基, 白春华, 等. 基于小波变换的爆破振动时频特征分析[J]. 岩石力学与工程学报， 2004, 23(1): 101.

LIN Dachao, SHI Huiji, BAI Chunhua, et al. Time-frequency characteristic analysis of blasting vibration based on wavelet transform [J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(1): 101.