8字结形格栅钢架腹筋力学作用试验研究

王 刚， 马兆飞， 卢 锋， *， 仇文革

(1. 西南交通大学交通隧道工程教育部重点实验室， 四川 成都 610031； 2. 蒙西华中铁路股份有限公司， 北京 100073)

0 引言

目前复合式衬砌已成为我国隧道建设的主要支护结构形式，在铁路、公路、城市轨道交通、水利水电工程中得到了普遍应用。复合式衬砌中初期支护通常采用喷锚支护配合型钢或者格栅钢架的结构形式，对于初期支护的力学特性，国内外研究者通过现场监测、模型试验和数值模拟等手段进行了研究，并取得了一定的成果。Braun[1]针对4杆结构格栅钢架形式，重点从格栅钢架的受力力学特性及经济性2方面进行了研究； 德国Baumann和Betzle等学者为了研究相对较新的结构，设计了一种腹筋为8字结构造的3肢格栅钢架，进行了一系列的试验研究和现场测试(试验类型分为格栅钢架和喷混凝土格栅钢架2种)，然后根据试验结果对结构内力进行了分析，并与理论结果进行了对比[2-4]； Nomikos等[5]对空钢架进行了一系列荷载试验和数值模拟，以格栅钢架的极限承载力和挠曲变形为判据，验证了在未喷混凝土情况下格栅钢架的受力特性和适用性； Kim等[6]提出了一种新型的4肢格栅钢架，并通过模型试验和数值模拟，将其与工字钢、三角形格栅钢架的极限承载力和稳定性进行比较，验证了新型格栅钢架的优点和适用性。

国内关于格栅钢架的最早研究是在20世纪80年代末西南交通大学[7-8]以及中国铁道科学研究院等单位进行的试验和工程应用。西南交通大学研究人员针对格栅钢架进行了室内环状模型试验，在内力分析、特性曲线和强度验算等方面积累了很多经验；原铁三院和中铁十六局等于1985年最早将几种截面形式的格栅支撑应用于大秦线的西坪隧道和军都山隧道中，后来相继在大秦线景忠山隧道、北京地铁复兴门折返线以及西单车站等工程中推广应用[9-11]； 李洪泉等[12]为评价格栅钢架喷混凝土支护的安全性，采用插值方法，在一些假设条件的基础上，结合位移监测情况，推导了由量测位移求支护内力的计算公式，并结合工程实例进行了验证分析； 张顶立等[13]通过室内性能试验和数值模拟，对型钢钢架和格栅钢架2种支护结构的受力特性、破坏过程及演化特性、极限承载力和变形量等进行了研究； 张德华等[14]针对存在极高地应力的大梁隧道，系统开展了型钢钢架与格栅钢架在高地应力软岩隧道支护中的适应性对比试验； 于富才等[15]按照高速铁路隧道Ⅳa围岩标准断面，分别采用普通钢筋和高强钢筋浇筑3组格栅混凝土复合支护构件，通过室内加载试验对3组构件的力学特性、隧道工程适用性和复合支护特性进行了研究； 龚铖[16]依托蒙(西)华(中)煤运铁路隧道，对单线H150型和双线H180型格栅钢架进行了模型试验和现场试验，对模型试验结构构件的变形规律、破坏形态和极限承载力进行了理论分析，并在此基础上进行了3种工况的现场试验，对试验段格栅钢架的受力情况、围岩收敛变形及围岩-初期支护接触压力进行了监控量测。

通过查阅文献及现阶段研究成果可以看出，目前对于格栅钢架的研究重点在于考虑支护与围岩相互作用下的支护结构受力特性以及对不同围岩的适用性，而对于格栅钢架本身力学特性及优化设计相关方面的研究较少。本文采用模型试验研究方法，系统研究了格栅钢架8字结腹筋直径和主腹筋焊缝长度的力学作用，为格栅钢架的优化设计提供依据。

1 试验设计

1.1 试验背景及方案设计

目前，国内在隧道建设中广泛使用的格栅钢架为4肢8字结设计形式，如图1所示。格栅钢架主筋采用对称配筋形式(4根主筋直径相同)，腹筋采用8字结结构形式。

本文以蒙西至华中地区铁路煤运通道(以下简称为蒙华铁路)为工程背景，选取蒙华铁路使用的H130、H150、H180和H230型号中最常用的H150、H180型格栅钢架作为研究的标准格栅钢架，用于试验对比，并对H150、H180型格栅钢架的用钢量进行了调研，每榀格栅钢架用钢量见表1。

(a) 8字结设计图

(b) 8字结加工图

表1 每榀格栅钢架用钢量

由表1可知： 1)腹筋的用钢量约等于4根主筋的用钢量，若可以通过优化减少腹筋的用钢量，则对格栅钢架的成本控制具有重大意义； 2)设计的格栅钢架主腹筋焊缝长度为7 cm，长度较大，在格栅钢架制作过程中增加了大量的人工和时间成本。

基于上述背景，本文采用模型试验方法，研究格栅钢架腹筋直径和主腹筋焊缝长度2个因素变化对格栅钢架力学作用的影响。考虑到格栅钢架的受力特征为压弯模式，试验过程中对试件进行偏心受压加载，并以偏心荷载作为试件的承载力指标。为了全面研究格栅钢架的力学特性，本文分别对格栅钢架和喷混凝土格栅钢架进行了研究，试验中采用HRB400钢筋和C25喷射混凝土制作试件。格栅钢架单独受荷试验工况设计见表2，喷混凝土格栅钢架试验工况设计见表3。需要说明的是，本文的目的是研究在相同受力条件下格栅钢架腹筋直径和焊缝长度变化对极限承载力的影响，考虑到格栅钢架的受力特征为压弯模式，故将试件设计为压弯构件。

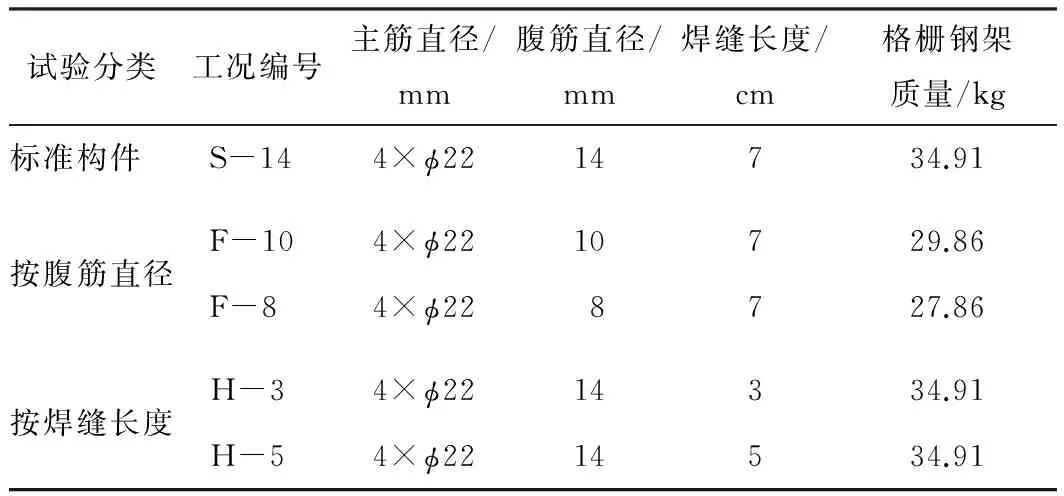
表2 格栅钢架单独受荷试验工况

注： 工况S-14为标准试验工况； 工况S-14、F-10和F-8中的数字代表钢筋直径； 工况H-3和H-5中的数字代表焊缝长度。

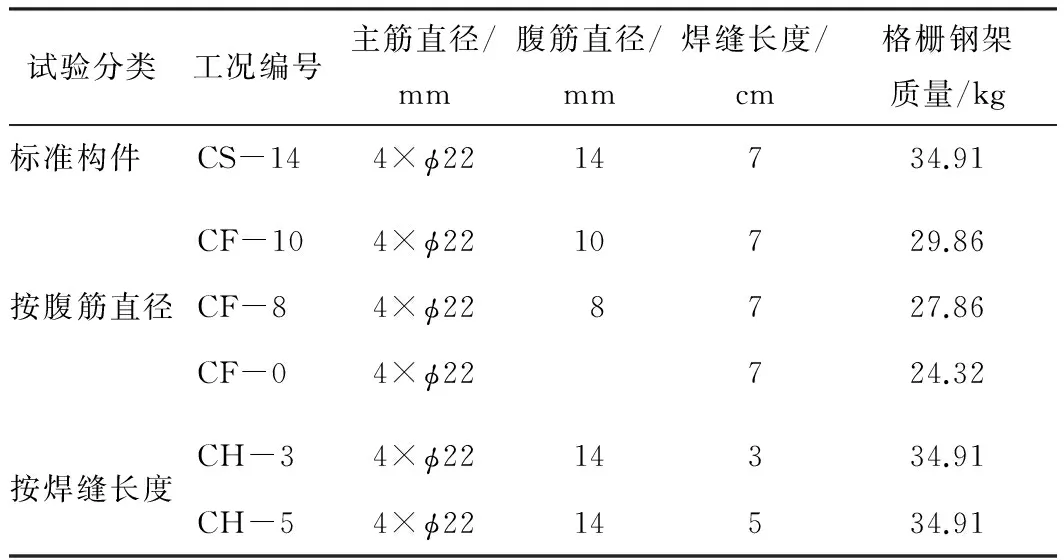
表3 喷混凝土格栅钢架试验工况

注： 工况CS-14、CF-10和CF-8中的数字代表钢筋直径； 工况CH-3和CH-5中的数字代表焊缝长度； 工况CS-14为标准试验工况，作为对比工况； 工况CF-0中未设置腹筋。

1.2 试验加载和量测系统

试验采用静力卧式加载装置，利用2台最大推进力为200 t的YQ-200型千斤顶配合1台DYB-LA型电动油泵提供稳定加载力，对试件施加偏心荷载，以此模拟结构的偏心受压模式。参照《铁路隧道设计规范》中按Ⅳ级围岩深埋隧道推荐的参数进行荷载-结构法计算，得到最大偏心距，并结合现场试验条件，试验空钢架偏心距取180 mm，混凝土试件偏心距取245 mm。试验装置输出的初始偏心力为85～103 kN，逐级加载约为18.5 kN。

试验中格栅钢架采用H150钢架，截面尺寸为150 mm×150 mm，混凝土构件截面尺寸为220 mm×220 mm。格栅钢架单独受荷偏心受压加载及量测装置如图2所示，喷混凝土格栅钢架共同作用加载及量测装置如图3所示。

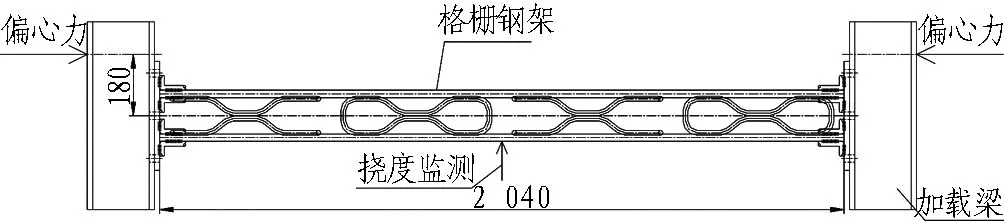
图2 格栅钢架单独受荷偏心受压加载及量测装置(单位： mm)

Fig. 2 Eccentric compression loading and experimental devices for lattice girder under single load (unit: mm)

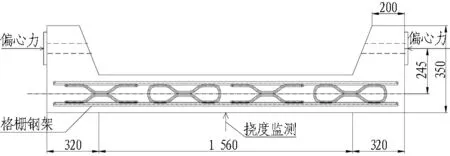
图3喷混凝土格栅钢架共同作用加载及量测装置(单位： mm)

Fig. 3 Experimental devices for shotcrete lattice girder (unit: mm)

2 格栅钢架优化指数

整个格栅钢架试验中既要考虑构件的承载力，又要考虑构件自身的经济性，为此引入隧道格栅钢架优化指数I，用以反映承载力与经济性双重因素的相关性。

(1)

式中：I为隧道格栅钢架优化指数；Pi为工况i构件的极限承载力，kN；mi为工况i构件的每延米质量，kg；Pb为标准构件的极限承载力，kN；mb为标准构件的每延米质量，kg。

优化指数反映了试验工况的“性价比”，数值越大性能越突出。I>1.0表示性能提高，I<1.0表示性能降低。需要说明的是，在计算优化指数时，只计算了材料用量，没有考虑人工成本和时间成本等费用。

3 试验结果分析

3.1 腹筋直径变化对力学作用的影响分析

8字结腹筋作为格栅钢架的组成部分，起着固定主筋、结构成型以及格栅钢架单独受力时传力的作用。腹筋直径的大小对格栅钢架加工、存放、运输和安装起着一定的作用。为此，在优化腹筋试验过程中设计了格栅钢架单独受荷和喷混凝土格栅钢架共同受荷2种受荷模式，便于综合分析格栅钢架在加工、存放、运输、安装过程中以及喷射混凝土与格栅钢架形成整体后的结构整体受力情况。

3.1.1 格栅钢架单独受荷

腹筋直径不同时格栅钢架单独受荷情况下试验结果见表4。由表4可以看出： 1)工况F-10中3组试件的平均极限承载力为147.22 kN，比标准工况S-14小9.16%，优化指数I较标准工况大6%； 2)工况F-8中3组试件的平均极限承载力为128.66 kN，比标准工况承载力小20.62%，优化指数I较标准工况小1%。

格栅钢架单独受荷情况下极限承载力、优化指数与腹筋直径的关系曲线如图4所示。由图4可看出： 试件极限承载力随腹筋直径的减小而减小，优化指数随腹筋直径的减小先增大后减小。工况F-8中极限承载力和优化指数均低于标准工况，且在试验过程中发现， 8 mm直径的钢筋刚度较低，构件在加工运输过程中容易变形，因此该种形式的设计不满足实际工程应用要求。工况F-10中极限承载力较标准工况下降幅度小，考虑到实际工程中隧道开挖完成格栅钢架施作后初期受荷较小，腹筋直径为10 mm时既可以保证格栅钢架施作初期的强度要求，也能满足格栅钢架加工、存放、运输和安装的要求，且优化指数大于1.0，较标准工况大6%，具有较好的经济性。需要说明的是，因为无腹筋结构理论上没有适用性，所以未对无腹筋工况进行格栅钢架单独受荷试验，仅将其作为格栅与喷射混凝土共同作用下一种极限情况的对比。

表4腹筋直径不同时格栅钢架单独受荷情况下试验结果

Table 4 Test results of lattice girder with different diagonal bar diameters under single load

试验工况极限承载力/kN试件1试件2试件3平均值构件质量/kg承载力与质量之比优化指数IF-10152.17141.03148.46147.2229.864.931.06F-8133.61133.61118.76128.6627.864.620.99S-14159.59170.73155.88162.0734.914.641.00

图4极限承载力、优化指数与腹筋直径的关系曲线(格栅钢架)

Fig. 4 Relationships among ultimate bearing capacity, optimization index and diagonal bar diameter of lattice girder

3.1.2 喷混凝土与格栅钢架共同受荷

腹筋直径不同时喷混凝土与格栅钢架共同受荷情况下试验结果见表5。由表5可知： 3种不同腹筋直径工况下试件的极限承载力均与标准工况相近，工况CF-10试件的平均极限承载力为296.13 kN，比标准工况CS-14大0.13%，优化指数比标准工况大17%； 工况CF-8试件的平均极限承载力为294.88 kN，比标准工况CS-14小0.29%，优化指数比标准工况大25%； 工况CF-0试件的平均极限承载力为308.60 kN，比标准工况CS-14大4.4%，优化指数比标准工况大41%。

喷混凝土与格栅钢架共同受荷情况下，极限承载力、优化指数与腹筋直径的关系曲线如图5所示。由图5可知： 随着腹筋直径的减小，构件极限承载力基本保持不变，但优化指数有较大提高，优化指数在工况CF-0时达到最大值，即腹筋直径的减小对喷混凝土格栅钢架的极限承载力影响不大，具有很好的经济性。工况CF-0的试验结果说明了喷混凝土后的格栅钢架腹筋对于承载力的提高没有作用，因此在满足格栅钢架加工、存放、运输和安装的前提下减小腹筋直径是可行的。综合格栅钢架单独受荷下的试验结果及现场加工情况，确定腹筋直径为10 mm时效果最优。

表5腹筋直径不同时喷混凝土与格栅钢架共同受荷情况下试验结果

Table 5 Test results of shotcrete lattice girder with different diagonal bar diameters

试验工况极限承载力/kN试件1试件2试件3平均值构件质量/kg承载力与质量之比优化指数ICF-10299.87292.39296.13296.1329.869.921.17CF-8296.13296.13292.39294.8827.8610.591.25CF-0307.36307.36311.10308.6024.3211.921.41CS-14284.80303.00299.40295.7334.918.471.00

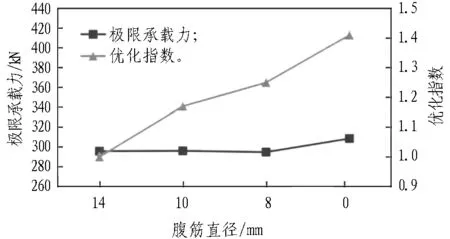
图5极限承载力、优化指数与腹筋直径的关系曲线(喷混凝土格栅钢架)

Fig. 5 Relationships among bearing capacity, optimization index and diagonal bar diameter of shotcrete lattice girder

3.1.3 不同腹筋直径的格栅钢架刚度

格栅钢架单独受荷和喷混凝土与格栅钢架共同受荷时不同腹筋直径工况下试件的荷载-挠度曲线如图6所示。由图6可以看出： 一方面，喷混凝土格栅钢架的极限承载力显著高于未喷混凝土时格栅钢架的承载力；另一方面，对于格栅钢架单独受荷和喷混凝土格栅钢架共同受荷试验，不同腹筋直径工况下试件的荷载-挠度曲线峰前斜率基本相同，表明腹筋直径的减小对格栅钢架的刚度基本没有影响。在实际工程中隧道开挖完成格栅钢架施作后初期受荷较小，格栅钢架真正发挥作用是在与喷混凝土形成整体承载结构以后。因此，在满足格栅钢架施作初期的强度要求和格栅钢架加工、存放、运输和安装要求的情况下，可以适当减小腹筋直径。

图6 不同腹筋直径工况下试件的荷载-挠度曲线

Fig. 6 Load-deflection curves of specimens with different diagonal bar diameters

3.2 主腹筋焊缝长度变化对力学作用的影响分析

3.2.1 格栅钢架单独受荷

格栅钢架单独受荷情况下焊缝长度不同时试验结果见表6。由表6可知，主腹筋焊缝长度不同情况下，试件的极限承载力相近。由此可见，主腹筋焊缝长度对格栅钢架单独受荷条件下试件的极限承载力无明显影响。另外，在试验中未出现因焊缝强度不足而导致结构破坏的现象，试件破坏模式如图7所示。格栅钢架单独受荷情况下极限承载力、优化指数与焊缝长度的关系曲线如图8所示。需要说明的是，在图8中，随着焊缝长度的减小，与标准工况相比优化指数没有明显增加，这是由于在计算优化指数时没有考虑人工成本和时间成本等费用。

表6格栅钢架单独受荷情况下焊缝长度不同时试验结果

Table 6 Test results of lattice girder with different welding lengths under single load

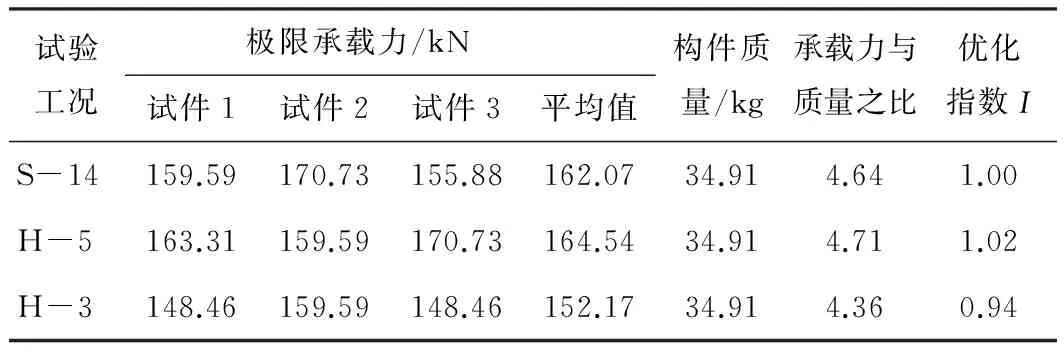
试验工况极限承载力/kN试件1试件2试件3平均值构件质量/kg承载力与质量之比优化指数IS-14159.59170.73155.88162.0734.914.641.00H-5163.31159.59170.73164.5434.914.711.02H-3148.46159.59148.46152.1734.914.360.94

3.2.2 喷混凝土与格栅钢架共同受荷

喷混凝土格栅钢架共同受荷情况下焊缝长度不同时试验结果见表7。由表7可知： 工况CH-5和CH-3试件的极限承载力与标准工况CS-14相近，说明在减小主腹筋焊缝长度后格栅钢架与喷混凝土共同受荷时试件的承载力并没有下降，且在试验中未发现焊缝处出现局部破坏的现象。喷混凝土与格栅钢架共同受荷情况下极限承载力、优化指数与焊缝长度的关系曲线如图9所示。

由于减小焊缝长度对提高格栅钢架加工效率、缩短人工作业时间十分有效，且通过试验说明减小焊缝长度是合理可行的。因此，结合格栅钢架单独受荷试验结果可知，焊缝长度为3 cm时钢架的经济适用性最好。

(a) 焊缝长度5 cm

(b) 焊缝长度3 cm

Fig. 7 Failure modes of lattice girder with different welding lengths

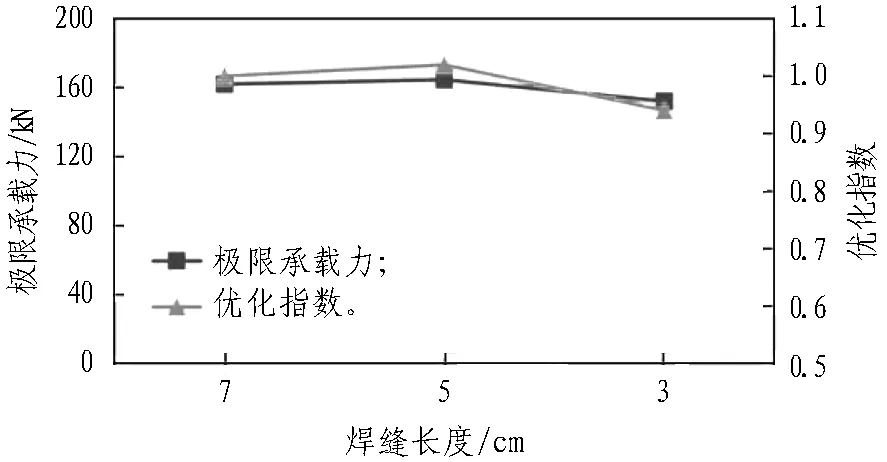
图8格栅钢架单独受荷情况下极限承载力、优化指数与焊缝长度的关系曲线

Fig. 8 Relationships among ultimate bearing capacity, optimization index and diagonal bar diameter with different welding lengths of plain lattice girder

表7喷混凝土与格栅钢架共同受荷情况下焊缝长度不同时试验结果

Table 7 Test results of shotcrete lattice girder with different welding lengths

试验工况极限承载力/kN试件1试件2试件3平均值构件质量/kg承载力与质量之比优化指数ICS-14284.80303.00299.40295.7334.918.471.00CH-5292.39307.36296.13298.6234.918.551.01CH-3314.84311.10314.84313.5934.918.981.06

图9喷混凝土与格栅钢架共同受荷情况下试件的极限承载力、优化指数与焊缝长度的关系曲线

Fig. 9 Relationship among ultimate bearing capacity, optimization index and diagonal bar diameter with different welding lengths of shotcrete lattice girder

3.2.3 不同焊缝长度的格栅钢架刚度

格栅钢架单独受荷和喷混凝土与格栅钢架共同受荷时不同焊缝长度工况下试件的荷载-挠度曲线如图10所示。由图10可知： 对于格栅钢架单独受荷和喷混凝土与格栅钢架共同受荷工况，焊缝长度减小至5 cm和3 cm 2种工况的极限承载力与对应的标准工况相近； 焊缝长度不同时，格栅钢架荷载-挠度曲线峰前斜率基本相同，说明焊缝长度的减小对格栅钢架的刚度没有影响。结果表明，主腹筋焊缝长度的减小，对格栅钢架的力学特性基本没有影响。

图10 不同焊缝长度工况下试件的荷载-挠度曲线

Fig. 10 Load-deflection curves of specimens with different welding lengths

4 结论与建议

本文采用模型试验方法，系统研究了腹筋直径和主腹筋焊缝长度对8字结形格栅钢架力学性质的影响，得到以下结论与建议：

1)喷混凝土格栅钢架共同受荷时，腹筋直径的减小对构件的极限承载力没有显著影响，但优化指数有较大提高，而且在不设置腹筋的情况下，构件承载力略高于标准构件承载力，说明腹筋对结构极限承载力的提高没有贡献。由格栅钢架单独受荷试验可知，腹筋直径为8 mm时格栅钢架承载力较低、易变形， 腹筋直径为10 mm时既能满足格栅钢架在加工、存放、运输以及安装过程中的刚度需求，又能在格栅钢架单独受荷时提供一定的承载力，且具有较好的经济价值，故建议将格栅钢架的腹筋直径优化为10 mm。

2)在格栅钢架单独受荷和喷混凝土与格栅钢架共同受荷2种受荷模式下，焊缝长度的减小对构件的极限承载力均未表现出明显影响，且试验中均未发现焊缝处出现局部破坏的现象，因此建议焊缝长度优化为3 cm。

3)综合分析可知，标准格栅钢架8字结腹筋用钢量与主筋相近，但却对其极限承载力基本没有贡献，性价比极低，故建议在进行格栅钢架设计时，可大幅减小腹筋直径，甚至可对其截面形式进行优化。

[1] BRAUN W M. Lattice girders offer econermy and performance for tunnel support[J]. Tunnels & Tunnelling International, 1983, 15: 19.

[2] BAUMANN T H, BETZLE M. Investigation of the performance of lattice girders in tunnelling[J]. Rock Mechanics & Rock Engineering, 1984, 17(2): 67.

[3] BETZLE M. Lattice girders giving arches a dig in the ribs[J]. Tunnels & Tunnelling, 1987, 19(11): 53.

[4] BETZLE M. Analyse statique et application de cadres relicules utilises en chantiers de tunnels[J]. Tunnels et Ouverages Souterrains, 1988, 86: 93.

[5] NOMIKOS P P, SOFIANOS A I, SAKKAS K M, et al. Nonlinear simulation of lattice girder segment tests[J]. Tunnelling & Underground Space Technology, 2013, 38(9): 180.

[6] KIM S, HAN T H, BAEK J S, et al. Evaluation of the structural performance of tetragonal lattice girders[J]. International Journal of Steel Structures, 2013, 13(1): 31.

[7] 仇文革. 格栅支撑的设计方法研究[D]. 成都： 西南交通大学, 1990.

QIU Wenge. Study of the design method of lattice girders[D]. Chengdu: Southwest Jiaotong University, 1990.

[8] 何林生. 地下工程格栅支护试验研究[D]. 成都： 西南交通大学, 1990.

HE Linsheng. Experimental study of lattice girders in tunnel and underground support[D]. Chengdu: Southwest Jiaotong University, 1990.

[9] 麦倜曾, 翁汉民, 仇文革. 西坪隧道格栅支撑的试验研究报告[C]//中国土木工程学会隧道及地下工程学会第五届年会论文集. 北京: 中国土木工程学会, 1988.

MAI Chouzeng, WENG Hanmin, QIU Wenge. Report of experimental study of lattice girders in Xiping Tunnel[C]//Proceedings of the 5th Annual Symposium of Tunnel and Underground Works Branch of China Civil Engineering Society. Beijing: China Civil Engineering Society, 1988.

[10] 何川. 隧道工程格栅支撑检算方法[J]. 铁道学报, 1990, 12(1): 66.

HE Chuan. The calculating method of lattice girders in tunneling[J]. Journal of the China Railway Society, 1990, 12(1): 66.

[11] 仇文革. 基于与围岩交互作用机理的格栅支撑特征曲线设计法[J]. 西南交通大学学报, 1996, 31(6): 640.

QIU Wenge. The characteristic curve design method of lattice girders based on the principle of interaction with surrounding rock[J]. Journal of Southwest Jiaotong University, 1996, 31(6): 640.

[12] 李洪泉, 杨成永, 徐明新, 等. 隧道格栅钢架喷混凝土支护安全性评价[J]. 岩石力学与工程学报, 2009, 28(增刊2): 3903.

LI Hongquan, YANG Chengyong, XU Mingxin, et al. Assessment on safety of lattice girder reinforced shotcrete support for tunnels[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(S2): 3903.

[13] 张顶立, 陈峰宾, 房倩. 隧道初期支护结构受力特性及适用性研究[J]. 工程力学, 2014, 31(7): 78.

ZHANG Dingli, CHEN Fengbin, FANG Qian. Study of mechanical characteristics and applicability of primary lining used in tunnel[J]. Engineering Mechanics, 2014, 31(7): 78.

[14] 张德华, 刘士海, 任少强. 高地应力软岩隧道中型钢与格栅支护适应性现场对比试验研究[J]. 岩石力学与工程学报, 2014, 33(11): 2258.

ZHANG Dehua, LIU Shihai, REN Shaoqiang. Research on selection of steel and steel grid for tunnel support in soft rock with high geostress[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(11): 2258.

[15] 于富才, 张顶立, 房倩, 等. 高强钢筋格栅混凝土复合支护特性的试验研究[J]. 土木工程学报, 2015, 48(9): 104.

YU Fucai, ZHANG Dingli, FANG Qian, et al. Experimental study of characteristics of composite support with high-strength reinforcing lattice girders embedded in concrete[J]. China Civil Engineering Journal, 2015, 48(9): 104.

[16] 龚铖. 隧道四肢8字结格栅钢架优化试验研究[D]. 成都： 西南交通大学, 2017.

GONG Cheng. Experimental study of optimization of four bar lattice girder with 8 diagonal steel bars in tunnel[D]. Chengdu: Southwest Jiaotong University, 2017.