检波器组合模型对比分析研究

代金芝，黄 鹏

（山西省煤炭地质115勘查院，山西大同037003）

为了解勘探区干扰波的发育情况，确定检波器的组合方式，在地震资料采集之前一般要做干扰波调查。检波器线性组合是最基本的组合方式，面积组合是多个线性组合的不同方式的叠加。盒子波技术是干扰波调查的一种有效手段，它将方形排列接收到的信号沿不同方位经切比雪夫加权组合制作成雷达图，从而研究干扰波的传播方向、速度、能量以及信噪比等。切比雪夫加权组合主要用于理论分析和室内检波器组合研究。因此，有必要研究切比雪夫加权组合和简单线性组合之间的关系，从而更好地为检波器组合提供理论依据和实践路线。

1 检波器简单线性组合的基本原理

假设地震波射线的入射角为α，用N个等灵敏度的检波器进行简单线性组合，取组内距为d，相邻检波器接收到波的延迟时间为Δt，则组合检波的时域方程为：

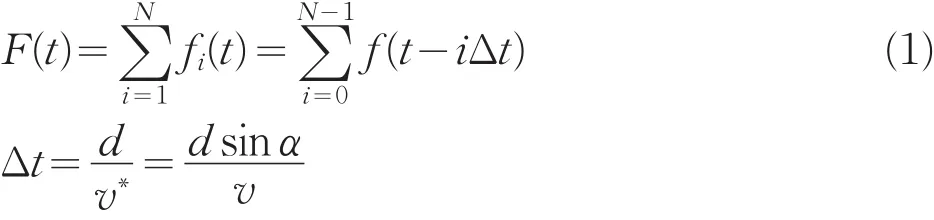
式中：v——真速度，m/s；

v∗——视速度，m/s。

将式（1）做傅里叶变换，得组合检波的频域方程为：

式中：ω——频率；

j——虚数单位；

N——检波器的个数；

g(jω)——第一个检波器输出信号的频谱；

k(jω )——滤波器的频谱[1]。

为了确定滤波器类型，分别画出k(jω)/N的单双边振幅谱，如图1和图2所示。

式中：d——组内距；

λ∗——视波长；

N——检波器的个数；

组合检波的方向特性曲线有以下特点：

（1）组合检波为低通滤波器。通带宽度为1/N；阻带为1/（2N）＜d/λ∗＜(2 N-1)/(2 N )，在阻带内，极值不一样；

（2） 当 d/λ*=(2 k+1)/(2 N)(k=1,2,…，N-2)时，阻带内有N-2个极点；

图1 7个检波器简单线性组合方向特性曲线（单边谱）

图2 7个检波器简单线性组合方向特性曲线（双边谱）

（3）当d/λ*=k/N(k=1,2,…,N-1)时，阻带内有N-1个零点。

2 检波器切比雪夫加权组合的基本原理

为了使阻带内极值相同，采用切比雪夫加权组合。引入以下函数作为滤波器加权振幅谱[3]：

式中:N——检波器个数；m=N-1；

ak——加权系数；

式中：d——组内距；

α——累积相位；

λ——波长；

Tm-2k(x)表示第m-2k次切比雪夫多项式，切比雪夫多项式是数学中常用的经验公式。切比雪夫多项式前2项分别为T0(x)=1和T1(x)=x，这是它的递推公式：

切比雪夫多项式前2项分别为T0(x)=1和T1(x)=x，其他项由如下递推公式算出：

由于x∈[-1,1]，不能构成一个有效空间滤波器[2]，因此将x扩展σ倍，则式(6)可表示为：

θ——入射角；

εm-2k——纽曼数，当m-2k=0时，其值为1,当m-2k≠0时，其值为2。

令x=cos(ψ/2)，将式（5）表示为切比雪夫多项式的函数为：

根据切比雪夫多项式的正交性，加权系数计算公式为：

当已知干扰波最小和最大波长λS和λL，则可算出组内距d，扩展因子σ，检波器个数N。

式中，压制比R=Tm(σ)。于是检波器切比雪夫加权组合的振幅谱可按式（5）、（7）、（8）、（9）算出。

3 实例分析

假设干扰波的最大和最小波长分别为λL=40m,λS=10m ，可求得组内距d=400/50=8(m)，扩展因子σ=sec(π/5)=1.24 。

当给定压制比R=29.5时，则检波器个数N=cosh-1(29.5)/cosh-1(1.24)+1=6.9989≈7。加权系数的矩阵表达式为：

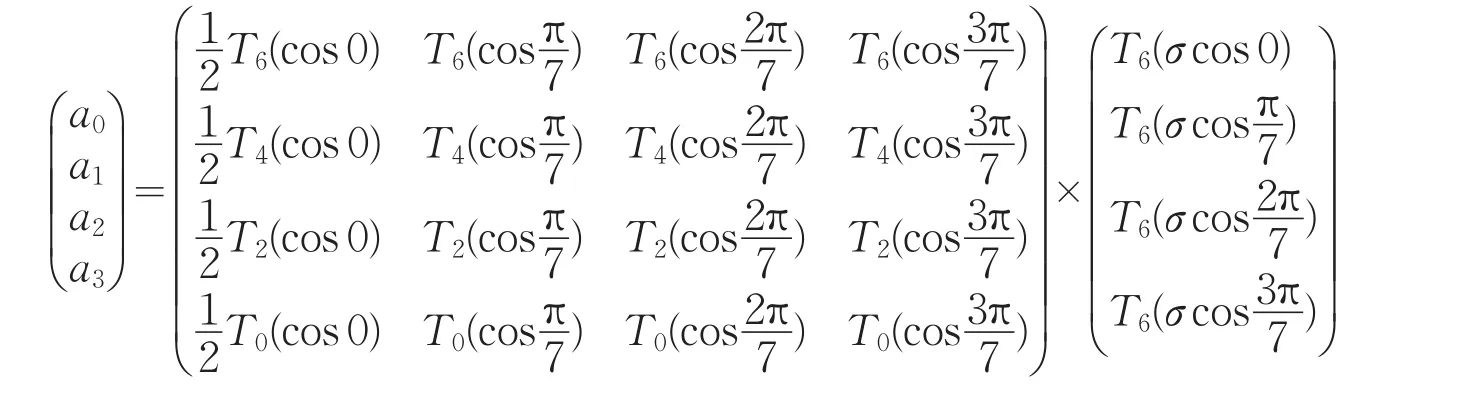
根据式（5）可算出切比雪夫加权组合的响应曲线，如图3、图4所示。

图3 7个检波器切比雪夫加权组合响应曲线

图4 7个检波器切比雪夫加权组合响应曲线（分贝表示）

切比雪夫加权组合响应曲线有如下特点：

（1）当d/λ*=cos(kπ /m)/σ,(k=1,2,…,m-1;m=N-1)时，阻带内有N-2个极点；

（2）当d/λ∗=cos{( 2k-1) π/(2m)}/σ，(k=1,2，…,m;m=N-1)时，阻带内有N-1个零点；

（3）阻带峰值具有相同值，不超过通带峰值的1/R，可用于计算信噪比；

（4）检波器组合基距(N-1)d≥λL。

4 结论

通过比较简单线性组合和切比雪夫加权组合可知：

（1）检波器简单线性组合是将检波器等间距、等灵敏度地做线性组合，利用干扰波与有效波传播方向差异来压制干扰波。

（2）切比雪夫加权组合实际上是对低通滤波器振幅谱进行加权，由于加权系数通常不全为整数，因此在实际工作中很难使检波器的灵敏度为加权系数，所以切比雪夫加权组合主要应用于室内组合及理论计算和研究，实际野外操作性差。基于这个局限性，盒子波干扰波调查方法中的雷达图是基于检波器切比雪夫加权组合而得到的，由于切比雪夫加权组合和实际检波器组合是有差异的，因此由雷达图得到的干扰波传播方向、速度、能量和信噪比等信息仅供野外采集参考。

[1] 朱广生，陈传仁，桂志先.地震勘探原理[M].武汉：武汉大学出版社，2005：204-230.

[2] 陆基孟.地震勘探原理[M].北京：中国石油大学出版社，1993：130-138.

[3] Mark Holzman.Chebyshev Optimized Geophone Arrays[J].Geo⁃physics，1963，28(2):145-155.