强非共沸工质R1234yf/R170/R14系气液相平衡的模拟

(上海理工大学制冷与低温工程研究所 上海 200093)

自动复叠制冷系统在小型制冷装置、天然气液化中具有较强的优势，能制取氮气液化温度77 K到常规单机压缩制冷温度230 K，常被用于气体液化、半导体加工、低温医学和低温生物等领域。国内外对自复叠节流制冷系统的研究较多，从两级到五级，从二元混合制冷剂到五元混合制冷剂。一般而言，200～230 K采用两级自复叠制冷系统，160～200 K采用三级自复叠制冷系统，120～160 K采用四级自复叠系统，70～120 K采用采用五级自复叠系统[1]。M. Ruhemann[2]将氟利昂制冷剂应用于自动复叠制冷系统，采用R13/R22混合制冷剂取得了200 K的低温。A. P. Kleemenko[3]采用摩尔比为65%/20%/15%的甲烷、乙烷和正丁烷的混合制冷剂通过单级压缩两级分离获得的低温成功液化了天然气，该制冷循环具有很高的热力学效率和运行可靠性，因此成为单流混合工质复叠循环(mixed refrigerant cascade cycle，MRC)。A. Fuderer[4]采用质量分数为20%/80%的R50/R12混合制冷剂成功获取了117 K的低温。此后，众多研究者不断改进自复叠系统，不断提高制冷效率，能获取的温度也越来越低[5-8]。李文林等[9-10]展开了对自动复叠制冷系统的研究，以R12/R13作为混合制冷剂，在70 L的低温箱中得到了218 K的温度，热力学效率为11.4%。Luo Ercang等[11-14]对混合制冷剂做了大量的研究工作，包括混合制冷剂热物性计算、系统优化和气液相平衡等方面。王国栋等[15-16]采用以R22/R23为混合制冷剂、单级压缩、单级分凝的自动复叠制冷系统，在4 h内成功将150 L的低温箱内温度降低到213 K以下，此后又以R134a/R23/R14为混合制冷剂，将冷箱温度降低到173 K，制冷量为38 W。此外，还对R600a/R23[17]、R600a/R23/R14/R740[18]、R245fa/R600a/R508B/R14[19]等混合制冷剂的自复叠系统做了相关实验研究，并对系统进行了改进，分析了系统降温特性、混合物分离汇合特性以及混合物的优化配比等多方面内容。随着人们对全球变暖、温室效应、臭氧层破坏等世界性环境问题的日益关注，制冷行业使用的制冷工质也加快了更新换代的步伐。自复叠系统中使用的制冷剂大多为氯氟烃(CFCs)和氢氯氟烃(HCFCs)类制冷工质，它们或对大气臭氧层有破坏作用，或具有很强的温室效应，或两者兼有。具有高全球变暖潜能值(GWP)和消耗臭氧潜能值(ODP)的制冷剂都将被逐步淘汰，新型环保制冷剂将逐步出现。

自复叠制冷系统结构相对简单，但混合制冷剂的工作机理复杂，涉及到很多理论基础知识，例如工质的分离与混合、混合工质传热、气液相平衡等。其中气液相平衡的研究尤为重要，它是对混合物基本物性的研究，以确定最佳工作状态、最佳配比等，影响整个系统的可靠性及运行效率。已有许多学者对混合制冷剂的气液相平衡进行了实验和模拟研究，但多数集中在近共沸工质，针对适用于多级自复叠系统的强非共沸工质的气液相平衡研究较少。Hu Peng等[20-25]对多组混合工质进行了气液相平衡研究并取得了一些相平衡数据，包括R1234yf/R600a[20]、R1234yf/R152a[21]，R1234yf/R161[22]、R134a/R600a/R1234yf[23]、R134a/R227ea和R143 a/R1234yf[24]，并通过实验数据结合理论模型对相平衡计算中的重要参数——二元相互作用系数kij进行了归纳总结[25]。J. Lia等[26]利用状态方程法对R125/R134a/R143a系进行了模拟研究，指出状态方程法能很好的预测混合物相平衡特性。Gong Maoqiong等[27-31]针对含R290的混合物进行了相关理论和实验研究。R. Budinsky等[32]采用Gibbs系综Monto Carlo(GEMC)模拟方法对两组混合物(R134a/R125和R134a/R32)进行了计算，计算结果与文献数据具有较好的一致性，并指出GEMC与以热力学为基础的Wilson和UNIFAC方法的预测精度相当。Q. N. Ho等[33-34]搭建了相关实验台，对二元混合物R1270/R134a和碳氢工质对R1270/R290的气液相平衡数据进行了实验，发现实验数据与采用Peng-Robinson状态方程(PR-EoS)结合Wong-Sandler(WS)混合法则的模拟结果吻合较好。以上学者多以实验的方法对混合物的气液相平衡进行研究。虽然实验方法是获取气液相平衡数据的第一手段，但仅仅通过实验无法取得大量的相平衡数据，因此通过有限的实验数据发展理论模型，提高预测精度，也是获取相平衡数据的重要途径[35]。

综合考虑各种制冷剂的物性参数，并结合三级自复叠制冷系统的特点和温度范围，本文对适用于三级自复叠制冷系统的R1234yf/R170/R14系混合制冷剂的气液相平衡数据进行了模拟计算。其中R1234yf是近年来被广泛使用新型制冷剂，且GWP<1，ODP=0，具有非常短的大气寿命(0.029 年)，被公认为是很有发展前景的环保替代制冷剂。R170为碳氢制冷剂，是天然工质，同时具备节能与环保的两大优势。R14的ODP=0，但GWP相对较高，虽然不是很理想的选择，但在目前情况下很难找到其对应温度段更好的替代工质。在理论模型的选择方面，超额吉布斯自由能-状态方程GE-EoS是继传统的状态方程法和活度系数法之后预测相平衡的一个新思路，此模型结合了状态方程法和活度系数法在相平衡预测方面的优点，并将极性体系预测能力非常强的活度系数模型直接应用于状态方程法的相平衡预测中。本文基于PR状态方程与WS混合法则，结合PSRK(Predictive-Soave-Redlich-Kwong)方程中使用的UNIFAC基团贡献法构建了混合物气液相平衡预测模型(PRWS-UNIFAC-PSRK)。利用此模型计算了二元混合制冷剂R161/R1234yf及三元混合制冷剂R32/R125/R134a的气液相平衡数据，并与相关文献的实验数据进行对比，验证了模型的精确度。在此基础上，对还未见有相平衡实验数据报道的R1234yf/R170/R14系混合物进行了模拟计算和分析，并给出了相关的相平衡图。这些相平衡特性对混合物的优化分离及相关自动复叠系统设计及改进都具有指导和借鉴意义。

1 方法及验证

1.1 模型选择

流体介质最基本的平衡物性参数即为压力-比容-温度(pvt)三者之间的关系，是研究流体其它热物性参数的基础。而体现流体pvt性质的方程式就是状态方程，因而对流体热物性的研究最终可归为对状态方程的获取。其中，两参数的立方型状态方程因其参数少，形式简单，计算精度高而备受研究人员的重视。应用状态方程法预测混合物气液相平衡特性，需要结合合适的混合法则，目前大多数文献中使用的模拟方法为van der Waals(vdW)法则，但是其在预测非理性体系时的精度并不高。为了克服这一缺陷，采用混合法则结合立方形状态方程及超额吉布斯自由能越来越多的在混合物气液相平衡的预测中使用。目前来看，还没有采用超额吉布斯自由能-状态方程模型(GE-EoS)对强非共沸的三元混合工质的气液相平衡特性的研究报告。本文利用PR状态方程和WS混合法则，结合PSRK方程中使用的UNIFAC活度系数模型，编译了相关模拟程序，对多组二元及三元混合物的气液相平衡数据进行了计算，并与参考文献数据和美国国家标准与技术研究院(NIST)数据库进行对比，验证了模型的准确性。在此基础上，对强非共沸工质R1234yf/R170/R14系的气液相平衡特性进行了模拟研究。

PR方程[36]的形式为：

(1)

(2)

(3)

kω=0.374 64+1.542 26ω-0.269 92ω2

(4)

表1 纯工质基本物性参数Tab.1 Basic physical parameters of pure components

WS混合法则[37]的基本形式为：

(5)

(6)

(7)

(8)

由PR方程和WS混合规则推导所得逸度系数求解方程为：

(9)

(10)

(11)

(12)

(13)

活度系数γi由改进的PSRK中使用的UNIFAC模型[38]计算得到：

lnγi=lnγiC+lnγiR

(14)

(15)

(16)

(17)

(18)

(19)

式中：Ni为混合物2组分的分子数;N为混合物总的分子数。用于WS混合法则中相关参数计算的各组分二元相互作用系数kij列于表2，它们由表3中的文献数据回归拟合得到。

表2 二元混合物的相互作用系数kijTab.2 Regressed kij from binary system

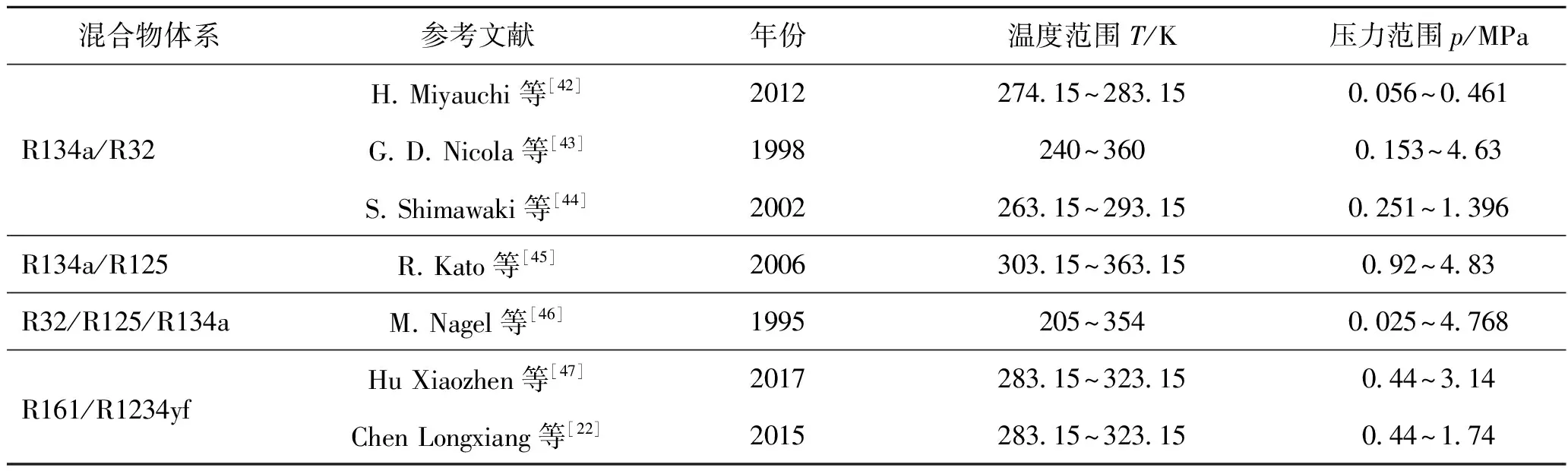
表3 混合物文献汇总Tab.3 Literature summary for mixtures

由于R1234yf/R170/R14系中各二元体系的气液相平衡数据未见有公开报道，因而相互作用系数采用Gong Maoqiong等[39-40]拟合的数值。用于活度系数和吉布斯自由能计算的UNIFAC-PSRK模型相关基团参数列于表4和表5。基团交互作用系数Amk是基团k和基团m之间相互作用能与两个m(k)基团之间相互作用能差异的度量(Amk≠Akm)，例如基团m为CH2,基团k为CF2时，Amk=42.257,Akm=-7.474。虽然表5中每一个主基团下子基团的Rk和Qk的值不等，但在同一主基团中所有子基团的交互作用系数是相同的，因而绝大部分的HFCs和HFO制冷剂的相平衡数据都可以通过三个主基团CH2、CF2和F的9个交互作用系数进行预测。本文参考吴献忠等[41]拟合的基团交互作用系数，对多组二元及三元混合工质进行气液相平衡预测。

表4 UNIFAC模型中的基团相互作用系数Amk和Akm[41]

表5 基团体积参数Rk和表面积参数Qk[41]

1.2 模型验证

为验证模型计算精度，本文选取已有文献实验数据的二元混合工质R161/R1234yf进行模拟计算，并将模拟结果与文献实验数据和美国国家标准与技术研究院(NIST)制定的REFPROP9.0软件数据库进行对比分析，如表6所示。

图1所示为R161/R1234yf系从283.15～323.15 K温度范围内压力与组分关系的对比，其中五角星和圆圈分别为实验测量的露点压力值和泡点压力值，实线和虚线分别为模型计算结果的压力露点线和泡点线。可以看出，实验数据点与计算结果的泡点和露点线吻合较好。图2所示为模型计算结果与实验数据的偏差，压力计算结果与实验值的相对误差基本在±1.5%以内，气相组分质量分数的绝对误差均在±0.02内，表明模型对二元混合工质气液相平衡特性的预测精度较高，满足实际工程应用的需求。

图1 R161(1)/R1234yf(2)系计算值与实验值的压力-组分关系Fig.1 Pressure-composition relationship between calculated results and experimental data for the R161(1)/R1234yf(2) system

图2 R161(1)/R1234yf(2)系计算值与实验值的误差关系Fig.2 Deviation between calculated results and experimental data for the R161(1)/R1234yf(2) system

图3 R161(1)/R1234yf(2)系计算值与REFPROP9.0数据库的压力-组分关系Fig.3 Pressure-composition relationship between calculated results and REFPROP9.0 database for the R161(1)/R1234yf(2) system

将模拟结果与REFPROP9.0数据库进行对比，如图3和图4所示。压力计算值与数据库的相对误差都在±5%以内，气相组分质量分数的绝对误差基本在±0.012 以内，表明模型的计算精度较高。观察图2可知，当R161的质量分数小于0.5时，压力偏差主要表现为正偏差，即实验值大于计算值，而气相组分质量分数主要表现为负偏差，即实验值小于计算值；当R161的质量分数大于0.5时，变化趋势刚好与上述情况相反。分析其原因如下：1)参考文献本身的测量误差；2)由于WS混合规则直接采用由低压气液平衡数据得到的活度系数模型参数和二元相互作用系数kij直接推算高压区气液相平衡，虽有良好的温度和压力外推性能，但依然会有一定的误差；3)采用PRWS-UNIFAC-PSRK模型对混合物进行气液相平衡预测时，需要建立在对混合工质基团分析的基础上，而UNIFAC基团贡献法主要应用于液相逸度的计算，气相逸度的计算还是采用状态方程，而状态方程在预测大分子化合物时比较困难，因而会出现负偏差的情况。因此，采用更高精度的状态方程以及对UNIFAC基团贡献法及参数进行更深入全面的分析研究，将会提高模型的预测精度和适用范围。

表6 温度为283.15～323.15 K时R161(1)/R1234yf(2)系气液相平衡数据

续表6

图4 R161(1)/R1234yf(2)系计算值与REFPROP9.0数据库的误差关系Fig.4 Deviation between calculated results and REFPROP9.0 database for the R161(1)/R1234yf(2) system

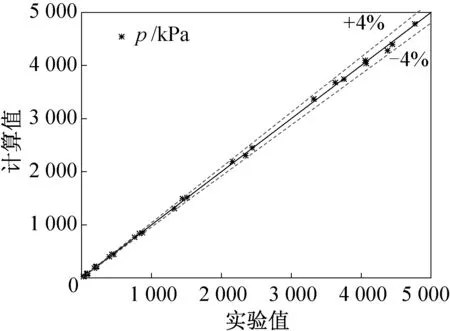
图5 R32(1)/R125(2)/R134a(3)系计算值与实验值的压力偏差关系Fig.5 Deviation of the pressures between the experimental data and the calculated data for the R32(1)/R125(2)/R134a(3) system

图6 R32(1)/R125(2)/R134a(3)系计算值与实验值的组分质量分数偏差关系Fig.6 Deviation of the vapor phase mass fraction between the experimental data and the calculated data for the R32(1)/R125(2)/R134a(3) system

为了验证模型对三元混合物气液相平衡的预测精度，对三元混合物R32/R125/R134a在组分质量配比分别0.272 1/0.126 8/0.601 1、0.191 0/0.433 2/0.375 8、0.097 6/0.705 7/0.196 7下的气液相平衡特性进行计算，并与文献[45]的实验数据进行对比，对比结果列于表7。图5所示为压力计算值与实验值的误差关系，图6所示为气相组分质量分数计算值与实验值的误差。由图5和图6可知，气相组分和压力的模拟结果与实验数据的偏差基本在±0.02和±4%以内，表明模型在预测三元混合物的时候亦具有较高的精度，满足实际工程应用的精度要求。虽然模型具有较好的预测效果，但不论是以无穷压力或零压力为参考态的GE-EoS模型在计算和预测非对称体系的气液相平衡时都会有一定的偏差，因此对GE-EoS模型进行进一步的扩展研究，如对UNIFAC的参数表进行修补和增订，以期GE-EoS模型在计算非对称体系和消除组合项差异时具有更好的预测效果，将会是下一步工作的重点。

2 R1234yf/R170/R14系等压气液相平衡研究

通过前文对二元混合物R161/R1234yf和三元混合物R32/R125/R134a的气液相平衡特性的研究，对比计算结果与实验数据，发现计算值与实验值具有很好的一致性。虽然在三元混合物的计算中直接采用二元体系中的相互作用系数，但模拟结果具有很高的可信度，表明模型在预测二元及三元混合制冷剂气液相平衡时具有较好的效果。在此基础上，利用PRWS-UNIFAC-PSRK模型对强非共沸工质R1234yf/R170/R14系的气液相平衡特性进行模拟研究。

图7 0.2 MPa压力下R1234yf/R170/R14系的三维立体相图Fig.7 Three-dimensional phase equilibria diagrams of R1234yf/R170/R14 ternary system at 0.2 MPa

图7～图10分别为R1234yf/R170/R14系在压力为0.2、0.5、1.5、2.2 MPa下的三维立体相图，其中靠上一面为露点面。露点面以上部分为气相区；靠下一面为泡点面，泡点面以下部分为液相区；泡点面和露点面之间的区域为气液两相区。从图中可以很直观的看到混合物组分、温度、压力及泡露点之间关系，红色越深，表明温度值越高。由于R1234yf、R170和R14三种制冷剂两两之间互为强非共沸工质，因而可以看到，泡点面与露点面之间的空间很大，即气液两相区范围很大，同时意味着混合物具有很大的滑移温度。通过数据筛选，混合物质量分数比为0.4/0.2/0.4时体系的温度滑移现象最为明显，最大的滑移温度达到72.5 K。对比图7和图10可发现，随着系统压力的增大，泡点温度和露点温度也随之上升，且R1234yf组分的质量分数越大，泡露点温度也越大。

表7 R32(1)/R125(2)/R134a(3)系气液相平衡数据[45]

图8 0.5 MPa压力下R1234yf/R170/R14系的三维立体相图Fig.8 Three-dimensional phase equilibria diagrams of R1234yf/R170/R14 ternary system at 0.5 MPa

图9 1.5 MPa压力下R1234yf/R170/R14系的三维立体相图Fig.9 Three-dimensional phase equilibria diagrams of R1234yf/R170/R14 ternary system at 1.5 MPa

图10 2.2 MPa压力下R1234yf/R170/R14系的三维立体相图Fig.10 Three-dimensional phase equilibria diagrams of R1234yf/R170/R14 ternary system at 2.2 MPa

在三级自复叠系统中，每级循环中两组分的标准沸点差值在40～80 K较合适，通过分析R1234yf/R170/R14系三维立体相图，可大致判断适用于实际工程应用的工况，对制冷装置的设计和改进、系统中工质组分的配比、混合物的优化分离、合适的运行温度及压力范围等具有很好的指导及参考价值，以提高系统运行效率。但由于还未见有相关实验数据的报道，本文的计算结果还无法进行实验对比验证，只能作为一种预测。未来将会对R1234yf/R170/R14系混合物的气液相平衡特性进行实验研究，提供更为准确的气液相平衡数据。

3 结论

本文利用混合工质气液相平衡计算模型(PRWS-UNIFAC-PSRK)对温度范围283.15～323.15 K和压力范围0.44～1.74 MPa下二元体系R161/R1234yf，以及200～350 K温度下三元体系R32/R125/R134a的气液相平衡特性进行了研究，并对比了计算结果与参考文献的实验数据。二元混合物R161/R1234yf的压力计算值与实验值相对误差基本在±1.5%以内，气相组分质量分数的绝对误差均在±0.02内；而三元混合物R32/R125/R134a的压力及质量分数偏差则分别在±4%和±0.02以内，说明模型对二元混合工质气液相平衡特性的预测精度较高，满足实际工程应用的需求。

利用文献已有的相互作用系数，对强非共沸工质R1234yf/R170/R14系在0.2、0.5、1.5、2.2 MPa下的等压气液相平衡特性进行模拟研究，并构建了相关的三维立体相图。混合物质量分数比为0.4/0.2/0.4时体系的温度滑移现象最明显，最大滑移温度达72.5 K。随着系统压力的增大，泡点温度和露点温度也随之上升，且R1234yf组分的质量分数越大，泡点温度和露点温度也越大。模拟结果对相关制冷系统设计及优化有一定的参考价值。采用多参数状态方程及改进活度系数模型，可进一步提高模型的预测精度。

[1] 芮胜军.带两路旁通的三级自动复叠制冷系统实验研究[D].上海:上海理工大学,2014. (RUI Shengjun. Experimental study on three stage cascade refrigeration system with two bypass[D].Shanghai: University of Shanghai for Science and Technology, 2014.)

[2] RUHEMANN M. The separation of gases[M]. 2nd ed. London: Oxford University Press,1949.

[3] KLEEMENKO A P. One-flow cascade cycle[C]//Proceedings of 10th International Congress of Refrigeration.Copenhagen, 1959.

[4] FUDERER A. Compression process for refrigeration:US3203194[P]. 1965-08-31.

[5] LITTLE W A, SAPOZHNIKOV I. Low cost cryocoolers for cryoelectronics[J]. Cryocooler, 1997, 9: 509-513.

[6] NAYAK H G, VENKATARATHNAM G. Performance of an auto refrigerant cascade refrigerator operating in gas refrigerant supply (GRS) mode with nitrogen hydrocarbon and argon-hydrocarbon refrigerants[J]. Cryogenics, 2009, 49(7):350-359.

[7] NARASIMHAN N L, VENKATARATHNAM G. Effect of mixture composition and hardware on the performance of a single stage JT refrigerator[J]. Cryogenics, 2011, 51(8): 446-451.

[8] REDDY K R, MURTHY S S, VENKATARATHNAM G. Relationship between the cool down characteristics of J-T refrigerators and mixture composition[J]. Cryogenics, 2010, 50(6/7): 421-425.

[9] 李文林.混合制冷剂的研究与发展[J].流体工程,1986,15(4):60-64. (LI Wenlin. Research and development of mixed refrigerants[J]. Fluid Machinery, 1986,15(4):60-64.)

[10] 李文林,华小龙. 混合工质制冷循环的试验研究[J]. 流体工程,1987,9(5):49-54. (LI Wenlin, HUA Xiaolong. Experimental study on refrigeration cycle of mixed refrigerant[J]. Fluid Machinery, 1987, 9(5):49-54.)

[11] LUO Ercang, GONG Maoqiong, ZHOU Yuan, et al. Experimental investigation of a mixed refrigerant T-T cryocooler operating from 30 to 60 K[J]. Advanced in Cryogenic Engineering, 2000, 45:315-322.

[12] WU J F, GONG M Q, LIU J L, et al. A new type mixture refrigeration auto-cascade cycle with partial condensation and separation reflux exchanger and its preliminary experimental test[J]. Advances in Cryogenic Engineering, 2002, 47:887-892.

[13] GONG Maoqiong, WU Jianfeng, LUO Ercang, et al. Further development of the mixture refrigeration cycle with a dephlegmation separator[J]. Cryocoolers, 2003, 12:603-608.

[14] GONG Maoqiong, WU Jianfeng, LUO Ercang, et al. Study of the single-stage mixed-gases refrigeration cycle for cooling temperature-distributed heat loads[J]. International Journal of Thermal Sciences, 2004, 43(1): 31-41.

[15] 王国栋.非共沸制冷剂自复叠制冷系统特性及应用研究[D]. 上海:上海理工大学, 2004. (WANG Guodong. Study on the characteristics and application of non azeotropic refrigerant auto cascade refrigeration system[D]. Shanghai: University of Shanghai for Science and Technology, 2002.)

[16] 陆向阳.三级自动复叠制冷循环的实验研究[D]. 上海:上海理工大学, 2002. (LU Xiangyang. Experimental study on three stage auto cascade refrigeration cycle[D]. Shanghai: University of Shanghai for Science and Technology, 2004.)

[17] 荆磊. R600a/R23自动复叠制冷系统及其应用[D]. 上海:上海理工大学, 2006. (JING Lei. Auto cascade refrigeration system and application of R600a/R23[D]. Shanghai: University of Shanghai for Science and Technology, 2006.)

[18] 刘红绍. 单级自动复叠制冷系统的实验研究[D]. 上海:上海理工大学, 2008. (LIU Hongshao. Experimental study on single stage auto cascade refrigeration system[D]. Shanghai: University of Shanghai for Science and Technology, 2008.)

[19] 朱军韬,张华. 混合工质Linde-Hampson 制冷系统的实验研究[J].制冷学报,2012, 33(2):18-23. (ZHU Juntao, ZHANG Hua. The experimental research on refrigerant mixtures of a Linde-Hampson refrigeration system[J]. Journal of Refrigeration, 2012, 33(2):18-23.)

[20] HU Peng, CHEN Longxiang, ZHU Wanbao, et al. Isothermal VLE measurements for the binary mixture of 2,3,3,3-tetrafluoroprop-1-ene(HFO-1234yf) + 1,1-difluoroethane(HFC-152a)[J]. Fluid Phase Equilibria, 2014, 373:80-83.

[21] HU Peng, CHEN Longxiang, CHEN Zeshao. Vapor-liquid equilibria for binary system of 2,3,3,3-tetrafluoroprop-1-ene (HFO-1234yf) + isobutane (HC-600a)[J]. Fluid Phase Equilibria, 2014, 365:1-4.

[22] CHEN Longxiang, HU Peng, ZHU Wanbao, et al. Vapor-liquid equilibria of fluoroethane (HFC-161) + 2,3,3,3-tetrafluoroprop-1-ene (HFO-1234yf)[J]. Fluid Phase Equilibria, 2015, 392:19-23.

[23] HU Peng, ZHU Wanbao, CHEN Longxiang, et al. Vapor-liquid equilibria measurements of 1,1,1,2-tetrafluoroethane (HFC-134a) + 2,3,3,3-tetrafluoroprop-1-ene (HFO-1234yf) + isobutane (HC-600a) ternary system[J]. Fluid Phase Equilibria, 2016, 414:111-116.

[24] HU Peng, CHEN Longxiang, CHEN Zeshao. Vapor-liquid equilibria for the 1,1,1,2-tetrafluoroethane (HFC-134a) + 1,1,1,2,3,3,3-heptafluoropropane (HFC-227ea) and 1,1,1-trifluoroethane (HFC-143a) + 2,3,3,3-tetrafluoroprop-1-ene (HFO-1234yf) systems[J]. Fluid Phase Equilibria, 2013, 360:293-297.

[25] 胡芃, 高敬轩, 陈龙祥, 等. PR方程结合vdW混合法则推算二元及三元HFC/HC混合工质汽液相平衡性质[J].化工学报, 2012, 63(2):350-355. (HU Peng, GAO Jingxuan, CHEN Longxiang, et al. Prediction of vapor-liquid equilibria for binary and ternary HFC/HC mixtures using PR equation of state and vdW mixing rule[J]. CIESC Journal, 2012, 63(2):350-355.)

[26] LIA J, TILLNER-ROTHB R, SATOA H, et al. Equation of state for hydrofluorocarbon refrigerant mixtures of HFC-125/143a, HFC-125/134a, HFC-134a/143a and HFC-125/134a/143a[J]. Fluid Phase Equilibria, 1999, 161(2):225-239.

[27] GONG Maoqiong, ZHAO Yanxing, DONG Xueqiang. Measurements of isothermal (vapor + liquid) equilibria for the (propane + cis-1,3,3,3-tetrafluoropropene) system at temperatures from (253.150 to 293.150)K[J]. The Journal of Chemical Thermodynamics, 2016, 98:319-323.

[28] GONG Maoqiong, GUO Hao, DONG Xueqiang. (Vapor + liquid) phase equilibria measurements for {trifluoroiodomethane (R13I1) + propane (R290)} from T=(258.150 to 283.150)K[J]. The Journal of Chemical Thermodynamics, 2014, 79:167-170.

[29] LIM J S,PARK J Y, KANG J W, et al. Measurement of vapor-liquid equilibria for the binary systems of propane + 1,1,1,2-tetrafluoroethane and 1,1,1-trifluoroethane + propane at various temperatures[J]. Fluid Phase Equilibria, 2006, 243(1/2):57-63.

[30] JU M, YUN Y,SHINM S, et al. (Vapour + liquid) equilibria of the {trifluoromethane (HFC-23) + propane} and {trifluoromethane (HFC-23) + n-butane} systems[J]. The Journal of Chemical Thermodynamics, 2009, 41(12):1339-1342.

[31] 陈秀萍, 祁影霞, 赵胜喜, 等. 新型二元混合制冷剂(R290 + R227ea) 气液相平衡研究[J]. 制冷学报, 2014,35(5):94-100. (CHEN Xiuping, QI Yingxia, ZHAO Shengxi, et al. Vapor-liquid equilibrium properties of new binary mixture refrigerant (R290 + R227ea)[J]. Journal of Refrigeration, 2014, 35(5):94-100.)

[32] BUDINSKY R, VACEK V, LISAL M. Vapor-liquid equilibria of alternative refrigerants and their binaries by molecular simulations employing the reaction Gibbs ensemble Monte Carlo method[J]. Fluid Phase Equilibria, 2004, (222/223):213-220.

[33] HO Q N, YOO K S, LEE B G. Measurement of vapor-liquid equilibria for the binary mixture of propylene (R1270) + propane (R290)[J]. Fluid Phase Equilibria, 2006, 245(1):63-70.

[34] HO Q N, LEE B G, PARK J Y, et al. Measurement of vapor-liquid equilibria for the binary mixture of propylene (R-1270) + 1,1,1,2-tetrafluoroethane (HFC-134a)[J]. Fluid Phase Equilibria, 2004, 225:125-132.

[35] 公茂琼, 吴剑锋, 罗二仓. 深冷混合工质节流制冷原理及应用[M].北京:中国科学技术出版社, 2014. (GONG Maoqiong, WU Jianfeng, LUO Ercang. The principle and application of throttling refrigeration for cryogenic mixtures[M]. Beijing: China Science and Technology Press, 2014.)

[36] PENG D Y,ROBINSON D B. A new two-constant equation of state[J]. Industrial & Engineering Chemistry Fundamentals, 1976, 15(1):59-64．

[37] WONG D S H, SANDLER S． A theoretically correct mixing rule for cubic equations of state[J]. Aiche Journal, 1992, 38(5):671-680．

[38] ORBEY H, SANDLER S I. Modelling vapour-liquid equilibria: cubic equation of state and their mixing rules[J]. Cambridge: Cambridge University Press, 1998.

[39] ZHANG Haiyang, GONG Maoqiong, LI Huiya, et al. A simple model for temperature-independent kij of the PR-vdW model for mixtures containing HCs, HFCs, PFCs, HFOs, CO2, RE170 and R13I1[J]. Fluid Phase Equilibria, 2016, 425:374-384.

[40] ZHAO Yanxing, GONG Maoqiong, DONG Xueqiang, et al. Prediction of ternary azeotropic refrigerants with a simple method[J]. Fluid Phase Equilibria, 2016, 425:72-83.

[41] 吴献忠, 崔晓钰, 李美玲. UNIFAC基团贡献法预测混合制冷剂的气液相平衡[J].化工学报,2005, 56(10):1832-1836. (WU Xianzhong, CUI Xiaoyu, LI Meiling. Estimation of refrigerant mixture phase equilibria with UNIFAC model[J]. CIESC Journal, 2005, 56(10):1832-1836.)

[42] MIYAUCHI H, YASUDA K, MATSUMOTO Y,et al. Isothermal phase equilibria for the (HFC-32 + HFC-134a) mixed-gas hydrate system[J]. Journal of Chemical Thermodynamics, 2012, 47:1-5.

[43] NICOLA G D, GIULIANI G,PASSERINIG, et al. Vapor-Liquid-Equilibria (VLE) properties of R-32+R-134a system derived from isochoric measurements[J]. Fluid Phase Equilibria, 1998, 153(1):143-165.

[44] SHIMAWAKI S, FUJII K, HIGASHI Y. Precise measurements of the vapor-liquid equilibria (VLE) of HFC-32/134a mixtures using a new apparatus[J]. International Journal of Thermophysics, 2002, 23(3):801-808.

[45] KATO R, NISHIUMI H. Vapor-liquid equilibria and critical loci of binary and ternary systems composed of CH2F2, C2HF5and C2H2F4[J]. Fluid Phase Equilibria, 2006, 249:140-146.

[46] NAGEL M, BIER K. Vapor-liquid equilibria of ternary mixtures of the refrigerants R32, R125and R134a[J]. International Journal of Refrigeration, 1995, 18(8):534-543.

[47] HU Xiaozhen, YANG Tao, MENG Xianyang, et al. Vapor liquid equilibria measurements for difluoromethane(R32)+2,3,3,3-tetrafluoroprop-1-ene(R1234yf) and fluoroethane(R161) + 2,3,3,3-tetrafluoroprop-1-ene(R1234yf)[J]. Fluid Phase Equilibria, 2017, 438:10-17.