管道内冰浆流动压降特性模拟和实验研究

(1 天津商业大学 天津市制冷技术重点实验室 天津 300134； 2 北京理工大学 北京 100081)

冰浆是一种水、冰晶粒子以及凝固抑制剂(比如氯化钠、乙醇等)组成絮状混合物，其中冰粒直径≤1×10-3m，一般冰粒子浓度大于5%时认为是非牛顿流体。冰浆作蓄冷介质具有良好的热物性、传输性及相变特性[1]，因此在建筑制冷、矿井降温、食品冷藏、医疗卫生和消防运输等领域都有应用[2-6]。近年来国内外许多研究者对冰浆的流动特性进行了研究，但主要是结合冰浆流动实验现象与非牛顿流体流变特性建立冰浆阻力特性预测模型。常用的非牛顿流体流变模型[7]有Bingham、Herschel-Bulkley、Powder Law和Casson，一些研究者针对这4种流变模型研究冰浆水平管道流动压降模型，M. Grozdek等[8]实验分析了在水平直管段内含冰率0%～30%条件下的压降特性。F. Illán等[9]以9%的NaCl溶液作为载流流体，分析了直管内的传热和压降特性。V. Ayel等[10]分析了冰浆的流动和传热特性，其中流动特性主要研究了直管内的压降特性。A. Kitanovski等[11]同样分析了冰浆的流动特性。然而，冰浆流动压降与管径、管型、流速、冰粒子浓度等有关，这些模型不能兼顾所有因素对流动压降的影响，而且由于模型采用的匀质流假设，只能用于低速分层流动，通用性和精度不高。

随着计算机技术和计算流体力学的发展，固液两相流的数值模拟也随之有了很大发展。常用的固液两相模型有以离散单元法(DEM)为基础的Euler-Langrian模型[12]和以颗粒动力学为基础的Euler-Euler模型[13]。Euler-Euler模型将颗粒相作为连续相，相对于Euler-Langrian模型计算量大为减小。将冰浆看作固液两相流体，利用Ansys Fluent研究冰浆的流动压降特性，但此方面研究尚不多见[14]。B. Niezgoda-Zelasko等[15]提出利用两相双流模型研究冰浆阻力特性，但冰粒子黏度模型仍将冰浆等效为均质流体，未考虑冰粒子的非均匀分布对黏度的影响，因此数学描述与实际流动存在一定的偏差。本文采用以颗粒相动力学为基础的Euler-Euler模型模拟冰浆在水平直管、90°弯管和T型管中的无相变流动压降，并用实验进行模型验证。

1 数学模型

描述冰浆流体等温流动的双流体计算模型[13]，数学描述可表示为：

1)连续性方程

(1)

由质量守恒方程，得:

(2)

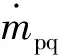
2)动量守恒方程

将冰浆看做液固混合的颗粒相流体，用液相动力参数描述动量方程[16]：

αqρqg+αq(Fq+Flift,q+FVm,q)+

(3)

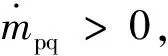
固体颗粒相动量方程为：

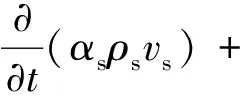
αsρsg+αs(Fs+Flift,s+FVm,s)+

(4)

液体相与颗粒相之间的作用力可用以下Gidaspow模型来[13]确定。

当αl>0.8时，液体-固体交换系数Ksl有如下形式：

(5)

其中：

(6)

当αl≤0.8时，Ksl有如下形式：

(7)

式中：Re为相对雷诺数。

主相q和第二相p的相对雷诺数：

(8)

3)湍流方程

本文采用k-ε湍流模型，该模型以N-S方程组为基础，同时考虑颗粒相和液相的相互作用[16]。

(9)

(10)

其中：

(11)

Gk,m=μt,m(um+

(12)

μt,m=ρmCμk2/ε

(13)

(14)

式中：C1ε=1.44；C2ε=1.92；σε=1.3；σk=1；Cμ=0.09;下标m为混合相；k为湍流脉动动能；μt,m为混合相湍流动力黏度， Pa·s；σk为湍流脉动动能的普朗特数；ε为耗散项。

4)黏度模型

冰浆是一种固液两相混合物，物理密度、动力黏度以及结冰点不仅受添加物浓度影响，还与含冰率有关，D.G.Thomas[17]通过反复实验和理论推算，得出黏度关于含冰率的公式：

μ=μl(1+2.5IPF+10.05IPF2+

0.002 73(e16.6IPF-1))

(15)

式中：IPF为含冰率。

2 数值模拟结果分析

借助模拟软件FLUENT进行流体计算，设定含冰率为10%和20%，冰晶粒子直径约为1×10-4m，管径为0.02 m；双精度并考虑重力影响，流速为0.2～10 m/s；边界条件在入口处设为速度入口，出口设为出流，壁面设为无滑移；求解器采用一阶迎风格式的SIMPLE算法；不考虑相变模型但开启能量源项，收敛精度设置为10-4，冰浆的基本参数见表1。

表1 冰浆的基本参数

1)水平直管

冰浆通过水平直管时，管道纵截面平均压力如图1所示，可以看出冰浆在水平直管中流动时压力一直下降，且入口的压降明显比出口大，造成这种现象的原因是入口处扰动较大，能量损失严重。

图1 水平直管纵截面平均压力分布云图Fig.1 The contour of pressure on the longitudinal section of horizontal tube

2)90°弯管

图2所示为90°弯管纵截面平均压力的分布云图。可以看出，拐角处的压力变化剧烈，压力损失严重，这是由于在拐弯处存在摩擦和二次流现象[18]，引起能量的损失。由于入口处扰动的影响，使入口压降大于出口压降。

图2 90°弯管纵截面平均压力分布云图Fig.2 The contour of pressure on the longitudinal section of the elbow tube

图3所示为弯管弯曲处冰粒子的速度矢量图，由此看出在弯管的弯曲处存在明显的二次流现象。当流体运动时遇到变向阻碍，弯道外侧近壁面边界层速度减小，离心力减小，而中心层速度较高，提供向心力的压力也较高，因此造成中心层向外层流动的趋势，形成附加流动，与此同时，还形成外侧向内侧的流动以保持质量守恒。二次流是主流与螺旋流动的叠加，因此能量损失极大。

图3 90°弯管的拐弯处管道横截面速度矢量云图Fig.3 The contour of velocity on the cross section of elbow tube

图4所示为90°弯管的管道纵截面冰浆速度分布云图，可以看出在流体转弯之前，固体冰粒速度逐渐增大，且有明显的边界层。在弯管弯曲处，有一个明显的高速漩涡出现，这是因为在离心力作用下流体向管道外侧运动，并逐渐外侧堆积，进而出现外侧向内侧的流动。流体离开转弯后，弯管外侧的速度较大，而内侧速度较小。

3)T型管

T型管形状较上两种都复杂，图5所示为T型管纵截面压力分布云图，左侧为冰浆进口，流体在三叉处分流至两个出口，其中上侧为出口1，右侧为出口2。

图4 90°弯管的管道纵截面冰浆速度分布云图Fig.4 The contour of velocity for the ice crystals on the longitudinal section of the tubes

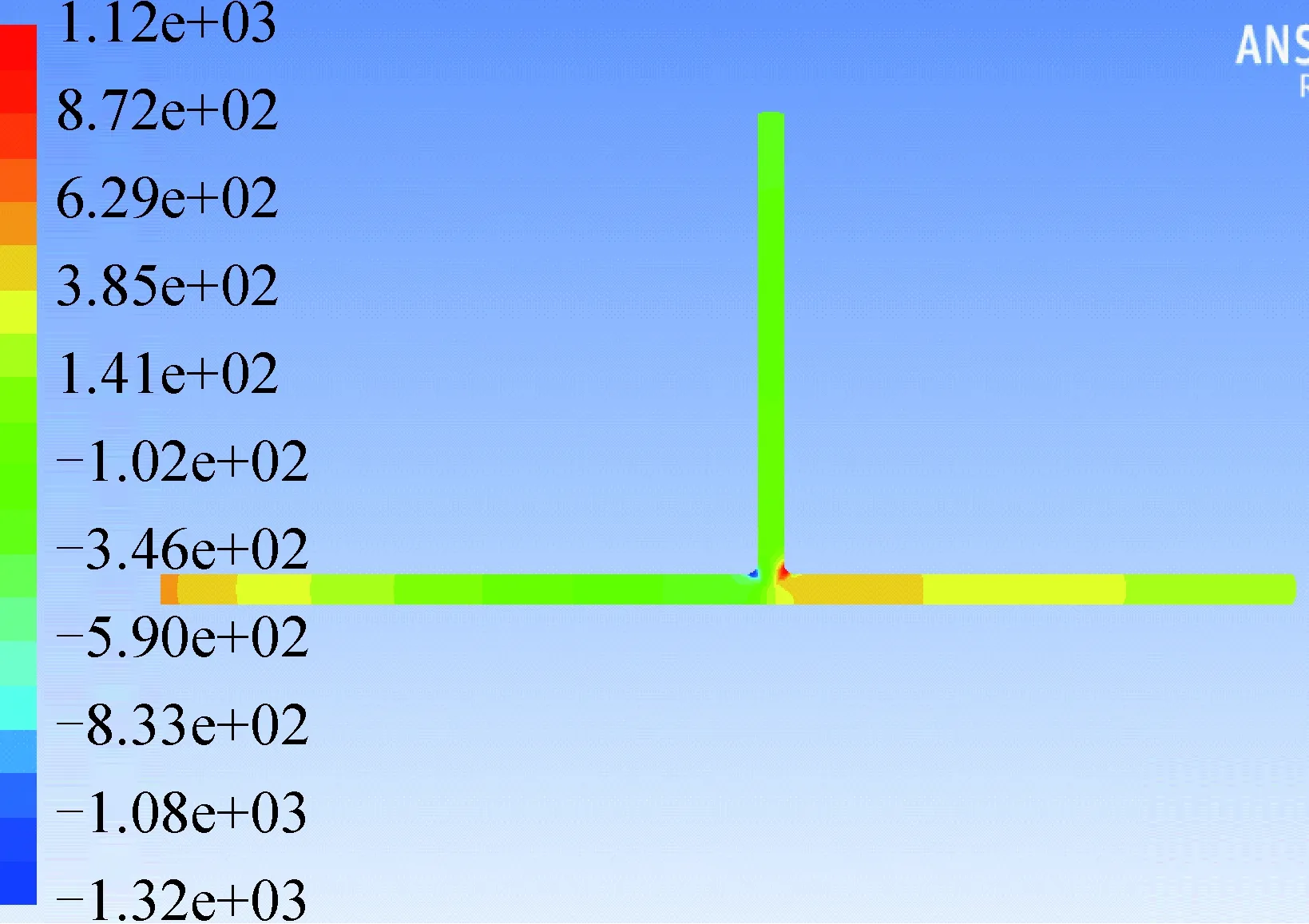
图5 T型管纵截面压力分布云图Fig.5 The contour of pressure on the longitudinal section of T-type tube

由图5可以看出，沿着冰浆流动方向压力变化趋势分明，从流动进口到分流之前，压力逐渐下降。在拐角处分流至两个方向，一个方向是垂直于来流方向，另一个方向为沿着原速度方向向前。拐角分流处液体压力剧烈变化，可以看出冰浆流经此处时有剧烈的湍流现象和能量交换，经过动量交换，冰浆在沿着来流方向的分流方向上压力剧增，然后又逐渐下降；而在垂直于来流方向的分流方向上，压力基本保持不变。值得注意的是垂直分流方向上的两个拐角出现一个压力最高点和最低点，最低点的出现是由于边界层脱落分离，造成压力突然降低；最高点的出现与90°弯管外侧的情况相似，都是由于能量交换使速度减小而压力增大。

图6所示为T型管纵截面冰浆平均速度分布云图，冰浆的平均速度除了在入口处有明显的变化外，在分流前基本保持不变，在分流处急剧下降至一定值，两个分流管内的流体平均速度基本相等。

图6 T型管纵截面冰浆平均速度分布云图Fig.6 The contour of average velocity for ice slurry

3 实验方法及过程

参考H. Kumano等[19-20]的实验方案设计如图7所示，实验系统包括4部分：冰浆存储装置、冰浆输送系统、流动实验测试段、数据采集系统。其中，冰浆存储装置是两个尺寸为0.395 m×0.395 m×0.025 m的不锈钢箱，外部包有10 mm厚的保温材料。冰浆输送系统由冰浆输送泵、过滤器、流量调节装置和输送管构成，冰浆输送泵采用可用于浆体的磁力驱动循环泵，过滤装置用于筛除粒径大于1×10-3m的冰粒子。流动实验段需要测量温度、压降和流量等物理量，实验测量装置的参数见表2。数据采集主要由GP10便携式无纸记录仪记录。测量段的3种管型采用的是管径为2×10-2m的黄铜管，管总长为1 m，且弯管和T型管均在中间位置有改变，弯管曲率半径为0.1 m，测试管水平放置，外包裹厚度约为1×10-2m的聚氨酯材料进行保温。

图7 流动实验段原理Fig.7 Principle of the flow experiments

表2 实验测量装置参数

实验前，先对仪表进行标定，温度校准设备为OPTI-CAL温湿度校验仪，精度±0.1 ℃；压力变送器经过Beamex多功能校验仪标定，INT160压力模块的量程为0～16 MPa，分辨率为0.000 1，精度为0.005%FS+0.0125%RDG。

实验时，储存箱1中的冰浆温度在-2 ℃左右，冰粒直径约为4×10-4～8×10-4m。IPF为10%～20%，流速在0.3～1.5 m/s选定5组。

冰浆的含冰率IPF用密度测量法计算为：

(16)

式中：ρslurry为溶液平均密度(质量与体积的比值，体积用量筒测量)，kg/m3；ρice、ρwater分别为冰和水的密度，kg/m3。

4 实验结果分析

1)管型对压降的影响

管道形状分为直管、90°弯管和T型管，3者之间对比分析的意义在于研究阻力部位的形状和阻力程度的关系。

图8 不同含冰率下3种管型内的压降随流速变化Fig.8 Variation trend of pressure drop in three piping shapes

由图8可以看出，压降受管型影响较大。含冰率为10%和20%，压降值从大到小依次为：T型管>弯管>直管。流速较低时，3种管道的压降值较接近，相差不大。流速越高，由于管型阻力不同，造成同流速下T型管与90°弯管、90°弯管与直管间压降差值变大。直管中没有阻力部件，因此压降主要是沿程损失，且直管部分的曲线可看出速度越高，压力损失越大。弯管中有一个弯曲部位，流动方向改变时，发生二次流，冰浆会撞击外侧壁面造成动量的损失，在竖直部分流动时，外侧流速大，质量多，故摩擦剧烈，压力损失较大。T型管分流后一支路沿原速度方向，另一支路转向90°，冰浆流经分流处遇到岔口，会形成漩涡，扰动更大。因此，在冰浆输送中，应尽量使用直管和弯管，T型管压降过大，尽量减少使用。

图9 直管压力损失系数与流速的关系Fig.9 Pressure lose coefficients in horizontal piping

流体流动时会产生沿程阻力，为了评价速度对压力损失的影响，参考流体力学中沿程损失和文献[21]，研究压力损失系数：

(17)

图9所示为直管压力损失系数与流速的关系，可以看出，水平直管中流速越大，压力损失系数越小，即对压降的影响越小。而流速与雷诺数成正比，且密度和黏度变化不大时，压力损失系数与雷诺数的关系与图9相同。

2)含冰率IPF对压降的影响

如图8所示，3种管型，IPF为20%的压降比IPF为10%的大。这是由于IPF越大，冰浆的非牛顿流体特征越明显，黏度也随固体颗粒的增多而增大。3种管型在高流速时的压降差高于低流速。这是因为速度小，冰水分层现象较为明显；随着速度增大，冰水混合逐渐均匀，颗粒效应使得黏度变大，因此压降差增大。当流速为0.9 m/s时，IPF从10%增大到20%时，直管压降从1.1 kPa/m增大到1.5 kPa/m； 90°弯管压降从1.9 kPa/m增大到2.1 kPa/m； T型管压降从2.27 kPa/m增大到2.73 kPa/m。由图8还可以看出，当速度增大到一定值时，弯管和T型管压降差值趋于恒定，原因是阻力部件存在，使得冰水掺混剧烈，易达到充分混合状态，此时，颗粒效应稳定，黏度差恒定，压降差基本不变。

3)实验与模拟结果对比

图10 压降模拟值与实验值对比Fig.10 Comparison of simulation results and experimental data for the pressure drop

图10所示为水平直管中实验数据与模拟数据的对比。由图可知数值模拟和实验的压降随流速的变化趋势一致，但在流速较大时，模拟值要大于实验值且误差达到20%，这是由于流速越大，冰浆流动的湍流程度就越大，冰颗粒与水的相互碰撞越剧烈，二者之间能量交换越多，相变影响越大，而数值模拟不考虑相变，所以模拟值与实验值偏差较大。

5 结论

本文从模拟和实验两个角度对冰浆在带有阻力部件的管道中流动特性进行了研究。管道的形状有直管、90°弯管和T型管3种，其中直管不含局部阻力部件，弯管带有一个弯曲处，T型管的连接部位是三通，带有两个弯曲处。主要研究了压降受含冰率、流速、管型的影响，结论如下：

1)从数值模拟的结果看，不考虑相变的影响时，3种管型在入口处都有明显的压降。对于弯管，在拐弯处出现二次流，压力变化较大；而T型管在三通处压力变化明显，甚至在垂直分流方向上的两个拐角分别出现压力最高点和最低点。

2)当实验条件和含冰率相同时，直管的压降最小，90°弯管次之，而T型管的压降最为严重。因此，在实际应用过程中应尽量避免T型管的使用。

3)冰浆各管型中水平方向流动时，压降都随着含冰率和流速的增大而增大。

4)水平直管中计算的沿程压力损失系数随速度的增大而降低。

5)直管的流动模拟结果与实验值误差在20%以内，在低流速时吻合较好。

本文受天津市应用基础与前沿技术研究计划项目(15JCYBJC21600)和天津市高等学校创新团队项目(TD12-5048)资助。(The project was supported by the Tianjin Research Program of Application Foundation and Advanced Technology (No.15JCYBJC21600) and the Science Research Innovation Team Project in Tianjin (No.TD12-5048).)

[1] EGOLF P W, KAUFFELD M. From physical properties of ice slurries to industrial ice slurry applications[J]. International Journal of Refrigeration, 2005, 28(1):4-12.

[2] DAVIES T W. Slurry ice as a heat transfer fluid with a large number of application domains[J]. International Journal of Refrigeration, 2005, 28(1):108-114.

[3] KAUFFELD M, WANG M J, GOLDSTEIN V, et al. Ice slurry applications[J]. International Journal of Refrigeration, 2010, 33(8):1491.

[4] BELLAS I, TASSOU S A. Present and future applications of ice slurries[J]. International Journal of Refrigeration, 2005, 28(1):115-121.

[5] 杜卫新, 郑光相. 冰浆制冷降温系统在平煤六矿的应用[J]. 煤炭工程, 2009, 365(4):63-65. (DU Weixin, ZHENG Guangxiang. The application of the ice slurry system for six coal mine in Pingdingshan Coal Group Co. Ltd.[J]. Coal Engineering, 2009, 365(4):63-65.)

[6] OTAKE H, SHITE J, PAREDES O L, et al. Catheter-based transcoronary myocardial hypothermia attenuates arrhythmia and myocardial necrosis in pigs with acute myocardial infarction[J]. Journal of the American College of Cardiology, 2007, 49(2):250-260.

[7] 何国庚, 王忠衡. 冰浆流体流动与换热研究综述[J]. 制冷学报, 2005, 26(4):1-5. (HE Guogeng, WANG Zhongheng. Review of study on flow and heat transfer of ice slurry[J]. Journal of Refrigeration, 2005, 26(4):1-5.)

[8] GROZDEK M, KHODABANDEH R, LUNDQVIST P. Experimental investigation of ice slurry flow pressure drop in horizontal tubes[J]. International Journal of Refrigeration, 2010, 33(2):357-370.

[10] AYEL V, LOTTIN O, PEERHOSSAINI H. Rheology, flow behaviour and heat transfer of ice slurries: a review of the state of the art[J]. International Journal of Refrigeration, 2003, 26(1):95-107.

[11] KITANOVSKI A, VUARNOZ D, ATA-CAESAR D, et al. The fluid dynamics of ice slurry[J]. International Journal of Refrigeration, 2005, 28(1):37-50.

[12] KUO H P, KNIGHT P C, PARKER D J, et al. The influence of DEM simulation parameters on the particle behaviour in a V-mixer[J]. Chemical Engineering Science, 2002, 57(17):3621-3638.

[13] GIDASPOW D. Multiphase flow and fluidization[J]. Multiphase Flow & Fluidization, 1994(95):1-29.

[14] MONTEIRO A C S, BANSAL P K. Pressure drop characteristics and rheological modeling of ice slurry flow in pipes[J]. International Journal of Refrigeration, 2010, 33(8):1523-1532.

[15] NIEZGODA-ZELASKO B, ZALEWSKI W. Momentum transfer of ice slurry flows in tubes, experimental investigations[J]. International Journal of Refrigeration, 2006, 29(3):418-428.

[16] 王继红, 王树刚, 张腾飞, 等. 水平管道内冰浆流体阻力特性CFD模拟[J]. 大连理工大学学报, 2012, 52(6):845-849. (WANG Jihong, WANG Shugang, ZHANG Tengfei, et al. Simulation of pressure drop for ice slurry flow in horizontal pipes by CFD[J]. Journal of Dalian University of Technology, 2012, 52(6):845-849.)

[17] THOMAS D G. Transport characteristics of suspension: VIII. A note on the viscosity of Newtonian suspensions of uniform spherical particles[J]. Journal of Colloid Science, 1965, 20(3):267-277.

[18] 王继红, 王树刚, 张腾飞, 等. 水平90°弯管内冰浆流体流动特性的数值模拟[J]. 高校化学工程学报, 2012, 26(4):581-586. (WANG Jihong, WANG Shugang, ZHANG Tengfei, et al. Numerical simulation of ice slurry flow in a horizontal 90° elbow pipe[J]. Journal of Chemical Engineering of Chinese Universities, 2012, 26(4):581-586.)

[19] KUMANO H, HIRATA T, SHIRAKAWA M, et al. Flow characteristics of ice slurry in narrow tubes[J]. International Journal of Refrigeration, 2010, 33(8): 1513-1522.

[20] MIKA. Ice slurry flow in a poppet-type flow control valve[J]. Experimental Thermal & Fluid Science, 2013, 45:128-135.

[21] MIKA. Pressure loss coefficients of ice slurry in horizontally installed flow dividers[J]. Experimental Thermal and Fluid Science, 2013, 45(2): 249-258.