基于遗传算法和BP神经网络的多联机阀类故障诊断

(1 华中科技大学能源与动力工程学院 武汉 430074； 2 空调设备及系统运行节能国家重点实验室 珠海 517907； 3 珠海格力电器股份有限公司 珠海 517907)

多联机具有节能高效、控制方便和安装灵活等特点，被广泛用于各种公共建筑物，其中多联机的电子膨胀阀和四通阀在制冷剂流量调节和流向转换上发挥着重要作用，一旦发生故障会导致舒适性降低，能耗增加。

神经网络、主元分析及决策树等算法[1-5]常用于故障诊断和检测的研究中，神经网络非线性映射能力较强，精度较高，适合求解多故障分类问题。结合相应的算法建模时，由于故障特征和故障类别的对应关系不清晰，一般采用大量原始故障特征进行建模，导致计算效率降低，严重时会降低诊断精度，所以需要对故障特征进行优化选择。遗传算法[6]是借鉴生物界自然选择和进化的随机化搜索算法，无需考虑函数的具体形式，非常适用于特征与参数的优化选择。姚文俊[7]介绍了遗传算法在故障诊断中搜索最优特征变量的应用。赵云等[8-9]利用遗传算法进行特征选择，从而大幅降低了分类系统的搜索空间。韩华等[10-11]利用遗传算法针对冷水机组故障特征进行选择，优化了特征空间，提高了故障诊断效率和正确率。段侯峰等[12-14]利用遗传算法优化各种基于神经网络的机械故障模型的结构参数，使模型更加精确。因此，本文利用遗传算法在优化选择上的优势，在原始特征集中搜索最优特征子集，与带参数优化的BP神经网络相结合，建立多联机阀类故障诊断模型，与基于原始特征集的神经网络故障诊断模型相比，故障检测及诊断正确率得到提高。

1 多联机阀类数据来源

本文以一台额定制冷量为45 kW，制冷剂为R410A的多联机系统为研究对象，该多联机实验系统如图1所示，共有5个室内机，编号为1、2、3、4、5，1个室外机，为保证多联机的正常运行，多联机上布有多个传感器，分别用来测量温度、压力、阀门开度、压缩机及风机频率等，共41个参数。其中温度测点与压力测点已在图上标出。首先，在制冷和制热工况下分别正常运行多联机系统，获得该多联机正常运行的数据。然后，进行阀类故障实验，故障实验分别为其中任意一个室内机电子膨胀阀卡死1(故障程度：卡在0开度)、电子膨胀阀泄漏、电子膨胀阀卡死2(故障程度：卡在最大开度)、四通阀故障，加上正常数据分别用标签A1-A5表示。神经网络输出结果中，采用向量表示各故障类型，1表示运行状况，越接近1，表示越接近运行状态。如表1所示。

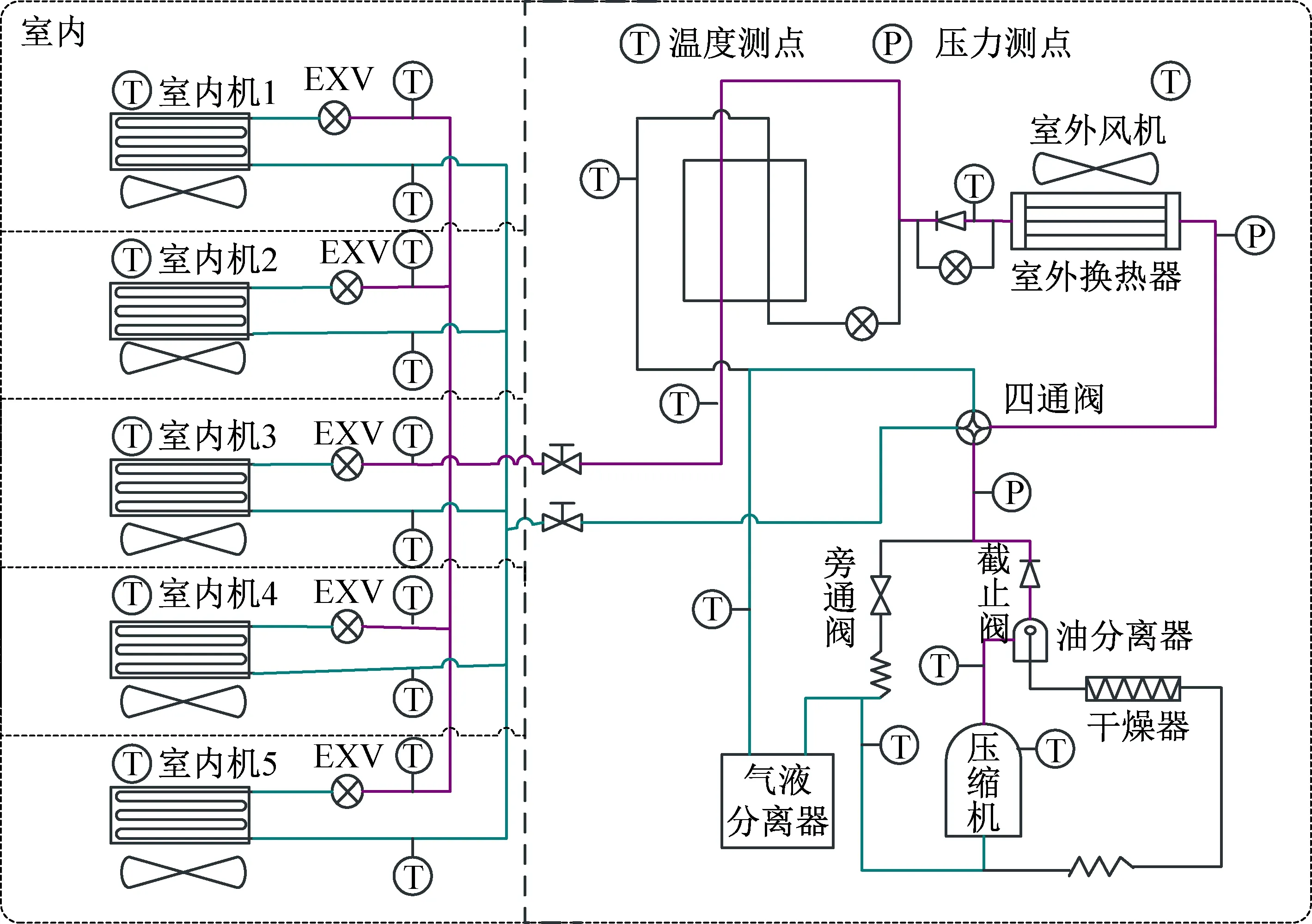
图1 多联机实验系统Fig.1 The VRF experimental system

表1 阀类故障类型的向量表示

2 多联机阀类故障诊断模型

多联机阀类故障诊断模型利用遗传算法对原始故障特征集进行优化选择，结合BP神经网络建模。

2.1 BP神经网络算法

BP神经网络[15]由于其函数信号正向传递，误差信号反向传播的特点，在神经网络中最重要、应用最多。如图2所示，BP神经网络由输入层、隐含层、输出层组成，通过不断调整权值、阈值达到期望输出。数据经输入层节点进入神经网络模型，通过传递函数传递到隐含层，隐含层可以是单层或者多层，隐含层将变换处理过的数据通过传递函数传递到输出层进行下一步处理。当实际输出与期望输出不符时，误差信号将反向传播，误差通过输出层，按误差梯度下降的方式逐层修正各层权值、阈值，函数信号的正向传递和误差信号的反向传播将反复进行直到满足期望输出。利用神经网络进行故障建模时，神经网络的参数如传递函数、训练函数、学习率以及隐含层节点数等直接影响故障分类的精度。

图2 BP神经网络结构Fig.2 BP neural network structure diagram

2.2 基于遗传算法的故障特征选择

故障诊断是针对诊断对象的故障模式进行分类和识别，或者根据专家经验等方法推断出故障所在部位和严重程度的过程，由于一种故障往往会伴随着多种故障特征，多种故障也可能引起同一故障特征，故障特征和故障类别的对应关系不清晰。因此，人们往往提出大量原始特征进行故障识别，降低了故障诊断效率，严重时会影响故障诊断正确率。遗传算法采用自选择、交叉遗传和变异等遗传过程寻找最优的故障特征集，如图3所示，具体步骤如下：

1)随机初始化一定数量的特征集：随机生成一定数量的二进制向量作为父代，每个向量代表一个随机特征集，即原始特征集的一个子集，整个二进制编码的长度为原始特征集中的特征数，1表示该特征存在，0表示特征不存在。

2)选择一定数量的父代进行交叉和变异：利用适应度函数评估种群的个体，按适应度值进行锦标赛选择，被选择的父代按一定的比例进行两点交叉和单点变异，生成子代。

图3 遗传算法特征选择的流程Fig.3 The flow chart of feature extraction based on GA algorithm

3)采用精英保留策略优化子代：变异操作之后比较当前最优个体与历史最优个体，并将最优个体直接复制替换最差个体，得到子代新种群。

4)找到满足条件的特征集：当遗传代数达到设定值，或者最佳适应度值基本不变时，继续迭代结果无明显改善，结束计算，否则回到2继续计算。用于评估种群个体好坏的适应度函数Ffitness为：

Ffitness=100(1-σvalve)+1

(1)

式中：σvalve为多联机阀类故障诊断的正确率。与神经网络相结合时，σvalve为利用神经网络进行故障分类的预测准确率。

优化特征变量是将某一特征是否参与建模为研究对象，每个特征变量只有存在和不存在两种可能，为典型的离散型变量，遗传过程针对二进制编码后的向量进行操作。本文的遗传代数设为100，群体规模为40，交叉概率为0.7，变异概率为0.017。

2.3 多联机阀类故障诊断复合模型

多联机的阀类故障诊断复合模型的执行流程如图4所示。首先，输入数据按比例随机划分为训练集和测试集，均进行数据归一化处理。然后，采用遗传算法针对训练集进行故障特征的选取和神经网络模型的训练，得到最优特征子集。同时对神经网络的参数如传递函数、训练函数、神经网络隐含层节点数等进行优化选择。最后，利用测试集对训练好的的神经网络模型进行测试，得到诊断结果。

2.4 多联机阀类故障诊断复合模型评价准则

采用混淆矩阵[16]比较真实故障分类和模型预测结果。模型的整体诊断率和各故障检测率分别为：

(2)

(3)

式中：σmodel为模型整体诊断正确率；σi为各故障检测率；Ci为第i个故障预测正确的个数；N为测试集的样本数；Ni为测试集中第i个故障的样本数。

图4 多联机的阀类故障诊断复合模型流程图Fig.4 The flow chart of the VRF valve fault diagnosis model

3 多联机阀类诊断性能结果分析

将实验稳态后的数据选取16 478个样本，并随机选取3/4的数据划分为训练集，1/4的数据划分为测试集。

3.1 BP神经网络参数优化选择

为了消除量纲的影响，将基于BP神经网络的多联机故障诊断模型的输入数据进行归一化，由于归一化的数据范围均在[-1,1]之间，故采用tansig正切s型传递函数。神经网络的输入层节点数设为故障特征个数，隐含层节点数、学习率等参数采用经验和试错法进行优化。

BP神经网络用于模式分类的常用训练函数[17]为：′trainrp′，′traingdx′,′trainscg′,′trainoss′, ′trainbr′, ′trainlm′。针对多联机阀类故障分类模型，采用建立不同训练函数进行建模，图5所示为不同的训练函数对故障诊断效率和正确率的影响。可以看出，这些训练函数相较于传统的梯度下降训练函数′traingd′，检测时间从250 s降到60 s以内(检测时间与电脑配置有关，为Intel(R)Pentium(R)CPU B940 (2.00 GHz),2.00 GB内存)，故障诊断正确率从70%提高到80%以上，训练函数的选择不同能显著提高故障诊断正确率及效率。其中′trainrp′和′trainbr′训练函数的检测时间均较少，检测正确率较高，达到95%，但′trainbr′(贝叶斯正则化算法)内存需求较大，故采用′trainrp′训练函数进行BP神经网络建模。

图5 不同训练函数对故障诊断效率和正确率的影响Fig.5 The influence of different training functions on the fault diagnosis accuracy and efficiency

3.2 采用原始特征集建立基于参数优化后的BP神经网络的故障诊断结果

将41个原始特征数据输入参数优化后的BP神经网络建模，得到的混淆矩阵如表2所示。

由式(2)可得，采用原始特征建立的BP神经网络的故障诊断正确率为：[741+463+585+1 031+1 038)/4 119]×100%=96.09%。

表2 基于原始特征集建模得的阀类故障混淆矩阵

由映射定理分析[18]可知，一个单层隐含层的BP神经网络能够以期望的精度逼近任意非线性函数，因而单层隐含层的BP神经网络故障诊断模型能够对多联机进行阀类故障诊断。

采用原始特征建立的BP神经网络故障诊断正确率为96.09%。由表2可知，电子膨胀阀故障的检测结果相对较差，其中，A1故障中有87个样本错误预测为A3故障，A2故障中有12个样本错误预测为A1故障，A3故障中有62个样本错误预测为A1故障。

3.3 基于GA优化后的BP神经网络故障诊断结果

按照图4流程所示建立基于遗传算法和神经网络的故障诊断模型，遗传代数设为100。适应度值的变化随着遗传代数的变化如图6所示。随着遗传代数的增加，适应度函数值先下降后保持不变，说明故障诊断率得到提高，并最终趋于稳定。

优化得到的模型诊断率由式(1)反推为：1-(1.728 3-1)/100=99.27%。优化后得到的故障混淆矩阵如表3所示。

对比采用原始特征集建立的BP神经网络的故障诊断结果与采用遗传算法优化特征集后的模型诊断结果，可以看出，相对于原始BP神经网络，用遗传优化得到最优特征子集后的神经网络模型整体故障诊断率和故障检测率均得到提高。

图6 适应度值随遗传代数的变化Fig.6 The fitness function value changes with genetic algebra

表3 基于特征优化后得到的阀类故障混淆矩阵

3.4 优化前后各故障的检测结果分析

优化前后各故障的检测率如表4和图7所示，only-BPNN为采用原始特征集建模检测结果，GA-BPNN为优化特征集后建模的检测结果。可以看出，采用原始特征集进行建模时，电子膨胀阀卡死1的故障检测率为89.49%，电子膨胀阀泄漏的检测率为97.47%，电子膨胀阀卡死2的故障检测率为89.72%。利用遗传算法优化后的电子膨胀阀的故障检测率均得到提高，电子膨胀泄漏的故障检测率达到100%，电子膨胀阀卡死1和电子膨胀阀卡死2的故障分别提高到98.21%和97.72%。本文利用遗传算法对多联机阀类故障的原始特征集进行选择提取最优特征子集，利用特征子集作为模型输入，降低了输入数据的维度，故优化后模型的运行效率提高，测试集的诊断与检测的耗时从23 s减至11 s，测试时间缩短了52.17%。

表4 两类模型检测正确率与耗时对比

图7 优化前后各故障检测率比较Fig.7 Comparison of fault detection rate before and after optimization

基于遗传算法筛选出的最优特征变量集为：室外环境温度、室内环境温度1、室内环境温度2、室内环境温度3、室内环境温度4、室内环境温度5、过冷器EXV、压缩机排气温度、模块高压、四通阀状态、过冷器气出温度、入管温度1、入管温度2、入管温度3、入管温度4、入管温度5、出管温度2、出管温度3，共18个特征变量(1、2、3、4、5代表对应室内机的编号)。结合专家经验可知，由于多联机的工作特性，每个室内机可以独立开启运行或关闭，通过室内环境温度和室外环境的对比，可以判断该室内机是否处于工作状态。制冷(制热)工况下，发生电子膨胀阀卡死1(卡在0开度)故障时，故障机的入管温度升高(降低)，且接近室内环境温度，其他室内机由于制冷剂流量变大导致出管温度降低(升高)；发生电子膨胀阀卡死2(卡在最大开度)故障[4]时，故障机的入管温度升高(降低)，其他室内机由于制冷剂流量变小导致出管温度升高(降低)。故障机发生电子膨胀阀泄漏[19]时，即不参与工作的室内机的电子膨胀阀发生故障不能完全关上，制冷剂从故障机泄漏，此时电子膨胀阀前后压差较大，节流孔径很小，节流后制冷剂的温度低，导致故障室内机的入管温度较低，由于泄漏的部分制冷剂于与空气进行自然对流换热，自然对流换热量很小，故压缩机排气温度降低。多联机的四通阀发生故障时，即在制热模式下会发生转向故障，低温低压的制冷剂仍流向室内机，此时模块高压降低，室内机进出管温度降低。可以看出，各阀类故障发生时，导致多个故障特征异常发生，遗传算法选出的特征变量子集能很好地表征故障发生后的异常变化。

4 结论

本文结合遗传算法和BP神经网络建立了一种针对多联机阀类故障的检测与诊断复合模型。该模型将多联机阀类故障实验得到的各阀类故障数据作为多联机阀类故障的原始特征集，利用遗传算法对特征集进行搜索，得到最优特征子集，以最优特征子集的数据作为参数优化后的BP神经网络的输入，从而诊断和检测出多联机的阀类故障。得到如下结论：

1)在建立基于BP神经网络的多联机阀类故障诊断模型的过程中，神经网络参数的优化能直接改善诊断性能。神经网络参数优化后，故障诊断正确率显著提高。

2)利用遗传算法对原始特征变量集进行优化选择，从41个特征变量中选择18个特征变量组成最优特征子集，相较于原始的特征变量集，利用最优特征集进行神经网络的建模，故障诊断正确率从96.09%提高到99.27%，测试时间缩短了52.17%，提高了故障检测及诊断正确率。

[1] 石书彪，陈焕新，李冠男，等.基于改进BP网络的冷水机组故障诊断[J].制冷学报, 2015, 36(6):34-39.(SHI Shubiao, CHEN Huanxin, LI Guannan, et al. Research on fault diagnosis of chillers based on improved BP network[J]. Journal of Refrigeration, 2015, 36(6):34-39.)

[2] 王江宇，陈焕新，刘江岩，等. 基于PCA-DT的多联机制冷剂充注量故障诊断[J]. 华中科技大学学报(自然科学版), 2016, 44(7):1-4.(WANG Jiangyu, CHEN Huanxin, LIU Jiangyan, et al. PCA-DT based refrigerant charge fault diagnosis for variable refrigerant flow system[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2016, 44(7):1-4.)

[3] 石书彪，陈焕新，李冠男，等. 基于小波去噪和神经网络的冷水机组故障诊断[J]. 制冷学报, 2016, 37(1):12-17.(SHI Shubiao, CHEN Huanxin, LI Guannan, et al. Fault diagnosis of chillers based on network and wavelet denoising[J].Journal of Refrigeration, 2016, 37(1):12-17.)

[4] GUO Yabin, LI Guannan, CHEN Huanxin, et al. Modularized PCA method combined with expert-based multivariate decoupling for FDD in VRF systems including indoor unit faults[J]. Applied Thermal Engineering, 2017, 115:744-755.

[5] GUO Yabin, LI Guannan, CHEN Huanxin, et al. An enhanced PCA method with Savitzky-Golay method for VRF system sensor fault detection and diagnosis[J]. Energy & Buildings, 2017, 142:167-178.

[6] GOLDBERG D E. Genetic algorithms in search, optimization, and machine learning[M]. Addison-Wesley Publishing Companly, Inc., 1989.

[7] 姚文俊. 基于遗传算法的故障诊断的研究[J]. 网络新媒体技术, 2004, 25(3):85-87.(YAO Wenjun. The study of fault diagnosis based on genetic algorithm[J]. Microcomputer Applications, 2004, 25(3):85-87.)

[8] 赵云，刘惟一. 基于遗传算法的特征选择方法[J]. 计算机工程与应用, 2004, 40(15):52-54.(ZHAO Yun, LIU Weiyi. Research on feature selection using genetic algorithms[J].Computer Engineering and Applications, 2004, 40(15):52-54.)

[9] 王世卿，曹彦. 基于遗传算法和支持向量机的特征选择研究[J]. 计算机工程与设计, 2010, 31(18):4088-4092.(WANG Shiqing, CAO Yan. GA-SVM-based feature subset selection algorithm[J]. Computer Engineering and Design, 2010, 31(18):4088-4092.)

[10] 韩华, 谷波, 康嘉. 基于遗传算法和支持矢量机参数优化的制冷机组故障检测与诊断研究[J]. 机械工程学报, 2011, 47(16):120-126.(HAN Hua, GU Bo, KANG Jia. Chiller fault detection and diagnosis based on genetic algorithm and support vector machine with parameter tuning[J]. Journal of Mechanical Engineering, 2011, 47(16):120-126.)

[11] HAN Hua, GU Bo, HONG Yingchun, et al. Automated FDD of multiple-simultaneous faults (MSF) and the application to building chillers[J]. Energy & Buildings, 2011, 43(9):2524-2532.

[12] 段侯峰. 基于遗传算法优化BP神经网络的变压器故障诊断[D].北京：北京交通大学, 2008.(DUAN Houfeng. Transformer fault diagnosis based on BP neural network optimized by genetic algorithm[D].Beijing: Beijing Jiaotong University, 2008.)

[13] 苗君明，佟刚，杨者青. 基于遗传算法的神经网络优化[J]. 沈阳航空航天大学学报, 2005, 22(3):30-32.(MIAO Junming, TONG Gang, YANG Zheqing. Artificial neural networks optimizing on genetic algorithm[J]. Journal of Shenyang Institute of Aeronautical Engineering, 2005, 22(3):30-32.)

[14] 袁圃，毛剑琳，向凤红，等. 改进的基于遗传优化BP神经网络的电网故障诊断[J]. 电力系统及其自动化学报, 2017, 29(1):118-122.(YUAN Pu, MAO Jianlin, XIANG Fenghong, et al. Grid fault diagnosis based on improved genetic optimization BP neural network[J]. Proceedings of the CSU-EPSA, 2017, 29(1):118-122.)

[15] 周开利. 神经网络模型及其MATLAB仿真程序设计[M].北京：清华大学出版社, 2005.(ZHOU Kaili. Design of neural network model and its MATLAB simulation program[M].Beijing:Tsinghua University Press, 2005.)

[16] ZHONG Qiu, YANG Liping, TAO Ye, et al. An optimized crossflow plate-fin membrane-based total heat exchanger[J]. Energy & Buildings, 2015, 86:550-556.

[17] 施彦，韩力群，廉小亲. 神经网络设计方法与实例分析[M].北京：北京邮电大学出版社, 2009.(SHI Yan, HAN Liqun, LIAN Xiaoqin. Neural network design method and case analysis[M].Beijing: Beijing University of Posts and Telecommunications Press, 2009.)

[18] 虞和济，陈长征，张省. 基于神经网络的智能诊断[J]. 振动工程学报, 2000, 13(2):202-209.(YU Heji, CHEN Changzheng, ZHANG Xing. Intelligent diagnosis based on neural networks[J]. Journal of Vibration Engineering, 2000, 13 (2):202-209.)

[19] 刘亚兵，朱伟，刘玉龙，等. 电子膨胀阀常见故障分析[J]. 制冷与空调(北京), 2013, 13(7):29-32.(LIU Yabing, ZHU Wei, LIU Yulong, et al. Common malfunction analysis of electronic expansion valve[J]. Refrigeration and Air-conditioning, 2013, 13 (7):29-32.)