R32和R32/R1234yf混合工质黏度实验测量及模型

(西安交通大学能源与动力工程学院 热流科学与工程教育部重点实验室 西安 710049)

制冷技术对人类社会的发展具有重要影响，20世纪30年代CFCs制冷剂的出现给制冷领域带来了飞速发展。1974年M. J. Molina等[1]指出含氯卤代烃对臭氧层有巨大破坏作用，由此引发了人们对制冷剂的广泛关注。氟利昂制冷剂对臭氧层的破坏作用迫使人们不得不寻找新的替代工质。国际社会达成了许多共识，如1985年制定的《维也纳公约》和1987年制定的《关于消耗臭氧层物质的蒙特利尔议定书》。随着CFCs和HCFCs类制冷剂的逐步淘汰，臭氧层消耗问题基本得到解决，但制冷剂对环境的另外一个负面影响地球温室效应问题日益严峻。1997年通过了《京都议定书》，限制温室气体的使用。2007年9月，蒙特利尔议定书第19次缔约方会议又通过了加速淘汰HCFCs的调整方案。2015年巴黎气候大会达成目标，各方将加强应对全球气候变化的威胁。对新一代替代制冷剂的研究也由保护臭氧层变为降低温室效应。为了履行议定书的承诺，我国制冷行业也同样面临巨大压力和挑战。

长期以来在替代制冷剂研究方面，国内外学者开展了大量的研究工作[2-6]。替代制冷剂必须满足基本要求：对臭氧层没有破坏作用，具有较低温室效应(GWP)和较高的效率[6]。除了CO2、水、氨及碳氢化合物(HCs)等自然工质外，在低GWP制冷剂替代方案中，烯烃类(HFOs)物质备受关注，最具代表性的物质是R1234yf和R1234ze(E)。但研究表明纯质R1234yf和R1234ze(E)的容积效率、制冷量以及COP相对较低[7]。R32的ODP=0，GWP100年=677[8]，相比于R22 (GWP100年=1 760)与R410A (GWP100年=1 725)，温室效应已有大幅改善，有可能成为我国未来一段时间制冷剂替代的过渡方案之一。但R32的排气压力较高，容易泄漏。因此，R32与R1234yf和R1234ze(E)形成混合工质，可以有效避免上述不足，是较好的解决方案[9]。此外，美国空调供热制冷协会(AHRI)主持开展的低GWP替代制冷剂评价项目(Low-GWP AREP)[3]，目前已完成第一阶段工作，部分新型混合制冷剂获得了ASHRAE标准命名和安全分级。R32、R1234yf、R1234ze(E)是其中最重要的组分。

工质的热物理性质是热力循环性能、制冷系统的优化、流动换热设备设计等方面研究的基础数据，具有重要的研究价值。其中，黏度性质在流动、换热等研究中必不可少，如计算雷诺数、普朗特数、努塞尔数等。R32和R1234yf纯质的黏度研究较多[10-19]，但其混合物黏度研究相对较少。Cui Junwei等[20]采用表面光散射法同时测量了R32/R1234yf混合物饱和状态下的液相黏度和表面张力。R32/R1234yf混合物实验测量温度范围为293～343 K，R32摩尔分数为0.519 3、0.698 8、0.794 5。Dang Yagu等[21]采用移动活塞式黏度计(moving piston viscometer)测量R32/R1234yf混合物液相黏度，测量范围温度为283～323 K，压力最高2.74 MPa, R32质量分数为0.3、0.5、0.7。Dang Yagu等[22]利用落球法黏度计测量了R32/R1234yf混合物气相黏度，测量范围温度为278～338 K，压力为0.1 MPa，R32质量分数为0.2、0.3、0.4、0.5。除此之外，未发现其他有关黏度文献发表。

通过以上文献调研发现，对于R32/R1234yf混合制冷剂液相黏度实验范围相对较窄，无法满足实际工况需求。此外实验是沿气液饱和态进行的，压力较低，缺乏高压状态下的实验数据。因此，本文主要工作是采用振动弦法黏度计对R32、R32/R1234yf混合物液相黏度进行实验研究，实验范围温度为263～360 K，压力最高为30 MPa。利用实验数据对R32/R1234yf混合物黏度模型进行研究。

1 实验方法与装置

本文采用振动弦法黏度计对混合制冷剂的黏度进行实验研究。振动弦法是由J. T. Tough等[23]于1963年提出的，基本原理是一根圆形截面无限长金属丝在黏性流体中，做垂直于轴向的振动，丝的运动与流体的黏度和密度有关，根据流体对振动的阻尼作用就可得到流体的黏度，其工作方程在文献中已有详细描述[18,24-25]，这里不再赘述，仅给出实验装置介绍。

振动弦选用名义直径为0.1 mm，长度为58 mm的钨丝，丝两端用金属夹片固定，固定时保持足够的张力，支撑结构采用陶瓷材料，以便绝缘。磁场由两块平行放置的钐钴磁铁(Sm2Co17)产生，两块磁铁间距为6 mm，磁铁的长度为40 mm，丝与磁铁长度比为1.45，中心丝的位置磁场强度约为0.4 T。振动弦传感器置于高压不锈钢腔体中，设计压力为70 MPa，采用金属垫片和法兰进行密封。钨丝两端各引出两根导线，连接测量电路和仪器，导线与实验装置采用玻璃陶瓷进行密封。实验装置本体约需60 mL样品。

振动弦黏度计实验测量系统原理如图1所示。主要由振动弦实验装置、增压泵、真空系统、恒温系统、温度压力测量系统及相应的数据采集软件等组成。增压泵为高压手动增压泵(型号50-6-15)，最大工作压力为100 MPa。压力测量采用P3MB型绝压传感器，最大测量压力为100 MPa，精度等级为0.1%。压力信号由安捷伦(Agilent)34420A型纳伏表采集，压力测量95%置信区间(k=2)扩展不确定度约为0.12 MPa。恒温环境由甲基硅油介质恒温槽提供，温度测量采用金属套管精密铂电阻温度计，电阻信号由安捷伦(Agilent)3458A采集，温度测量95%置信区间(k=2)扩展不确定度约为12 mK。

A增压泵；B真空泵；C试剂瓶；D压力传感器；E振动弦实验装置；F恒温系统；G温度传感器。图1 振动弦黏度计实验系统原理[18]Fig.1 The principle of vibrating wire viscometer[18]

振动弦的驱动信号由安捷伦(Agilent)信号发生器33220A产生，产生的感应信号由SR830(Stanford Research System)数字锁相放大器采集。振动弦黏度测量系统的标定和检验过程见文献[18]，标定的结果丝的半径R=49.60 μm，真空下阻尼系数Δ0=1.96×10-5。振动弦黏度测试系统的不确定度主要由温度不确定度、压力不确定度、标定不确定度和复现不确定度等构成，最终黏度测量扩展不确定度估计为2%(k=2)。

2 实验结果与分析

2.1 实验样品

实验所用R32由浙江蓝天环保高科技股份有限公司生产，其纯度为99.8%的样品(质量百分比)，R1234yf由霍尼韦尔(中国)有限公司提供，样本的纯度为99.5%(质量百分比)，制冷剂样品信息如表1所示。实验采用液氮冷却收集气相样品，并抽真空除去杂质和不凝性气体。

表1 实验所用样品信息

2.2 混合物样品配制及配比测量

本文配制混合制冷剂的方法为：首先收集两种纯质制冷剂，按照配比确定收集量，然后按照饱和蒸气压高低，先将饱和蒸气压较低的R1234yf充灌到实验本体中，再将饱和蒸气压较高的R32充灌到实验本体，充灌温度低于环境温度，以保证实验本体中全部为液相状态，实验测量的最低压力也高于该温度下对应的饱和压力。混合制冷剂的组分通过从实验本体中直接取样并由气相色谱(安捷伦7820A)分析确定，组分分析的不确定度为0.005。

2.3 实验结果

本文对制冷剂R32、R32/R1234yf混合物的黏度进行了实验测量。R32黏度测量实验温度范围为263～350 K，压力最高为30 MPa，实验沿6条等温线共获得36组实验数据，如表2所示。R32/R1234yf二元混合物黏度的温度范围为263～360 K，压力最高为30 MPa，R32摩尔分数分别为0.244 8、0.410 8、0.608 6、0.835 6，实验沿8条等温线共获得141组实验数据，数据如表3～表6所示。

振动弦法测量黏度需要准确的密度数据，因此必须选用合适的状态方程计算相同温度和压力下的密度值。R32的密度数据由R. Tillner-Roth等[26]开发的状态方程计算得到，R32/R1234yf混合物密度数据由R. Akasaka[27]开发的状态方程计算得到。不同温度和压力下对应的制冷剂密度数据如表2～表6所示。

3 实验数据分析

3.1 黏度模型

为了便于工程实际应用，本文利用硬球模型[28-29]关联了R32和R32/R1234yf的黏度实验数据，该模型的具体表达式为：

(1)

式中：η*为无量纲黏度;η为黏度，Pa·s；M为摩尔质量，kg/mol；T为温度，K；通用气体常数R=8.314 472 J/(mol·K)；V为摩尔容积，m3/mol；Rη为形状因子。无量纲黏度η*为摩尔容积V和特征摩尔容积V0比值的函数：

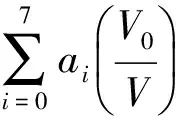
(2)

表2 R32黏度实验数据

表3 R32/R1234yf混合物黏度实验数据(xR32=0.244 8)

表4 R32/R1234yf混合物黏度实验数据(xR32=0.410 8)

表5 R32/R1234yf混合物黏度实验数据(xR32=0.608 6)

表6 R32/R1234yf混合物黏度实验数据(xR32=0.835 6)

式中：ai为系数;V0为温度的函数，一般是随温度升高而下降。通过数据拟合得到每个温度下的V0，以及与温度压力无关的Rη，并将V0拟合成如下表达式：

V0×106=a+bT+cT2+dT3

(3)

最终得到R32黏度关联式的拟合系数和偏差，如表7所示，实验数据与方程的平均绝对偏差(AAD)为0.28%，最大偏差(MD)为0.92%，二者均在实验不确定度范围之内。

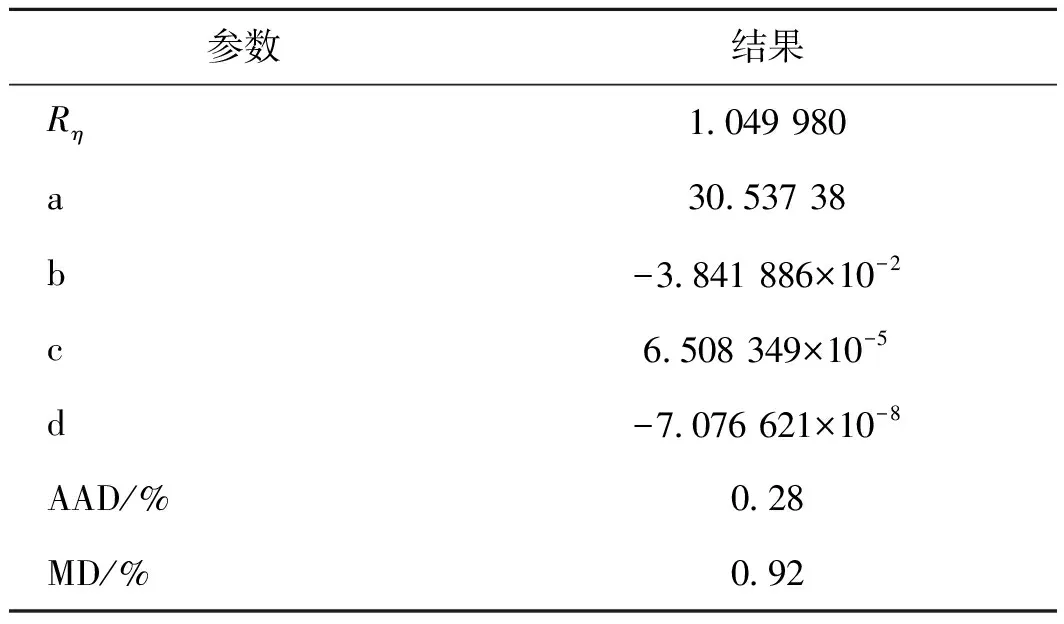
表7 R32黏度方程式(1)～式(3)拟合参数及偏差

为了将该模型应用于二元混合物R32/R1234yf黏度数据关联，Rη,mix和V0,mix采用如下的混合规则计算：

Rη,mix=xRη,1+(1-x)Rη,2

(4)

(5)

γ=αT+β

(6)

式中：Rη,i和V0,i为纯组分i的形状因子和特征摩尔容积；x为组分1的摩尔分数。对于特征摩尔体积，引入参数γ修正温度的影响。得到R32/R1234yf混合物黏度关联式的拟合系数和偏差，如表8所示，实验数据与方程的平均绝对偏差为0.69%，最大偏差(MD)为2.09%。可知黏度硬球模型不仅可以准确的描述纯质的黏度特性，同时也可以表征混合物的黏度特性。

3.2 实验数据对比

本文测得的R32黏度实验数据与拟合方程的偏差如图2所示。V. Z. Geller等[10]测量了253.15～347.15 K，压力最大达到5 MPa范围内的黏度，偏差最大为7.7%，尤其是随温度变化趋势明显。M. J. Assael等[11]测量了273～313 K，压力最大达到15 MPa范围内的黏度，最大偏差为4.9%，最小偏差为3.6%。此外，测量了饱和态下273～313.15 K的黏度，最大偏差为5.3%，最小偏差为4.3%，与其他作者数据比较可以知，M. J. Assael等[11]的数据存在一定的系统偏差。A. Laesecke等[14]测量了饱和态下250～315 K范围内的黏度，偏差为正负波动，最大偏差为-1.38%。Sun Liqun等[15]测量了饱和态下233～333 K范围内的黏度，最大偏差为5.6%。C. M. B. P. Oliveira等[16]测量了饱和态下230～345 K范围内的黏度，除了高温一个点偏差为8.9%，其余偏差都在3%以内。R. Heide等[17]测量了饱和态下223～333 K范围内的黏度，大部分数据偏差在2.5%以内。

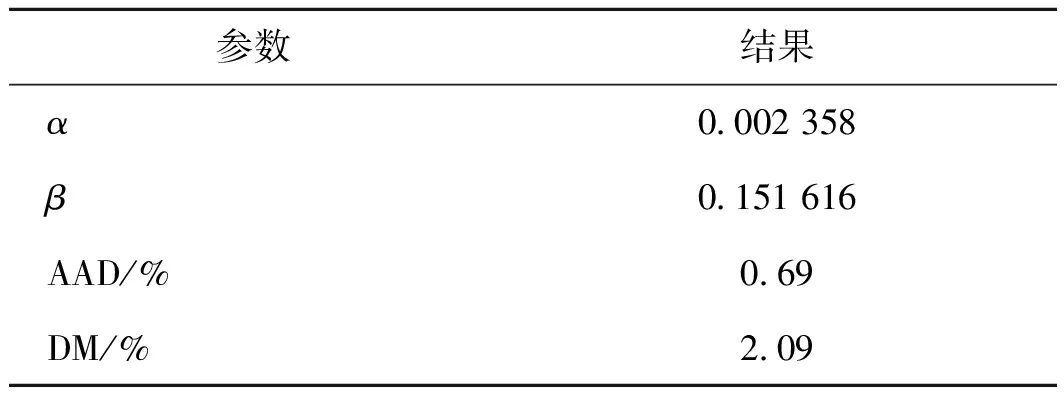
表8 R32/R1234yf黏度方程式(5)～式(6)拟合参数及偏差

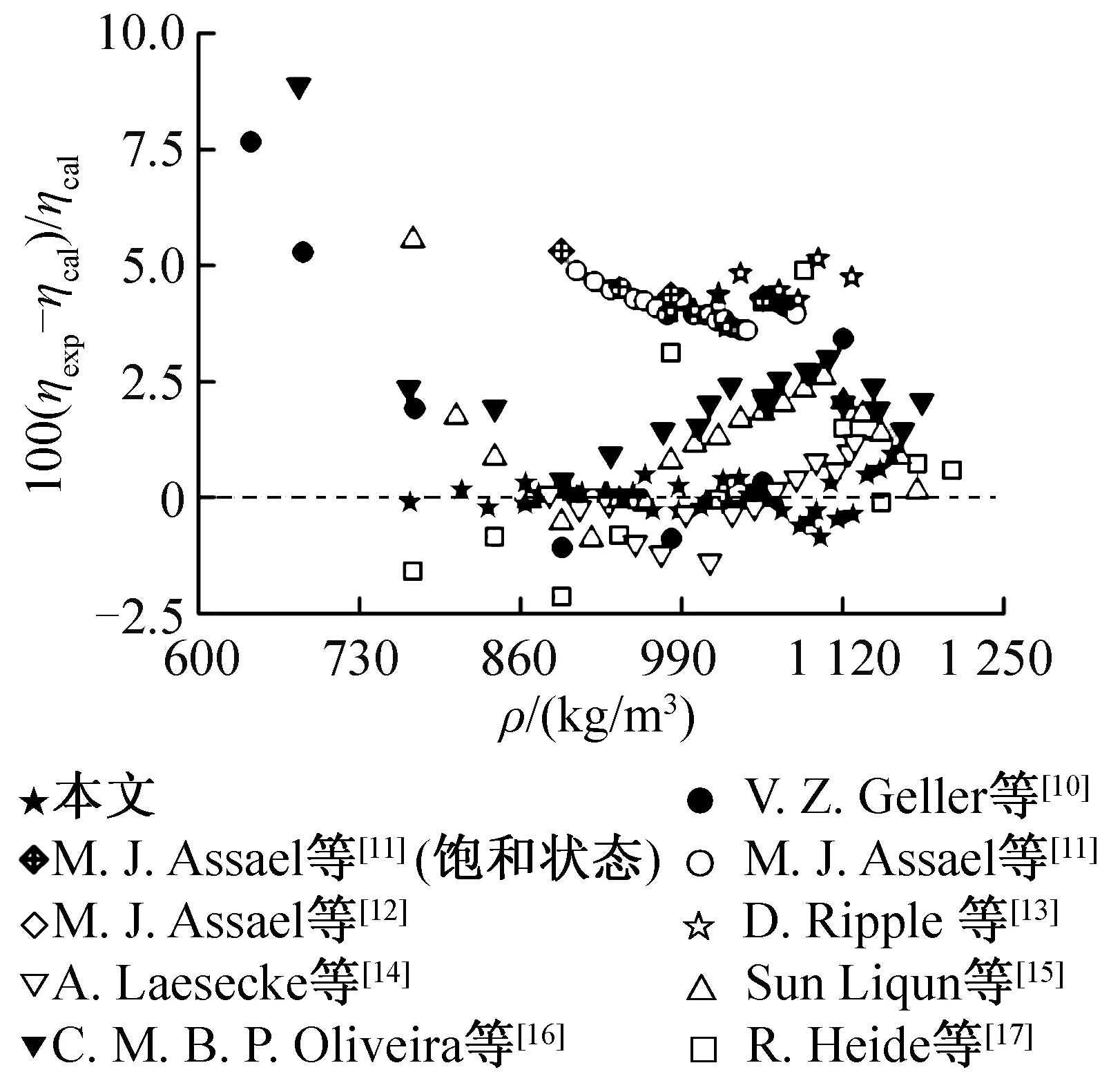
图2 R32黏度实验数据与关联方程的偏差Fig.2 Deviations for R32 of the experimental viscosity from calculated values obtained with the correlation

本文实验测量的R32/R1234yf混合物黏度实验数据与拟合方程的偏差如图3所示。Dang Yagu等[21]采用移动活塞式黏度计测量了R32/R1234yf混合物温度范围283～320 K液相黏度，其中R32的质量分数分别为30%、50%和70%。实验数据与本文方程偏差全部为正偏差，最大偏差为12.9 %，最小偏差为0.5%，在每个配比下，都会出现偏差随温度增大而增大。Cui Junwei等[20]采用表面光散射法同时测量了R32/R1234yf混合物液相表面张力和黏度，温度范围为293～343 K，R32的摩尔分数为0.519 3、0.698 8和0.794 5。实验数据大部分为负偏差，除了343 K温度下对应的3个数据点偏差较大，其他数据偏差都在6%内。Cui Junwei等[20]的实验数据与NIST REFPROP 9.0的计算结果进行了比较，其偏差趋势与本文硬球模型关联得到的方程相似。两组文献实验数据与本文实验数据或方程都有较大偏差，但一组为正偏差，一组为负偏差。出现此种现象的原因可能是实验过程中混合物比例发生变化，由于实验腔体中为气液相共存，而配制好样品后实验在不同温度下完成测量，气液相中的比例也不断发生变化，组分变化关系取决于样品配制和实验过程。本文在实验过程中保证腔体中全部为过冷液相区，并且液相区中组分大小是直接通过气相色谱仪测量确定，因此本文实验结果有良好的准确性。

图3 R32/R1234yf黏度实验数据与关联方程的偏差Fig.3 Deviations for R32/R1234yf of the experimental viscosity from the calculated values of the correlation

4 结论

本文对R32及R32/R1234yf混合制冷剂不同温度、不同压力下的液相黏度进行了实验研究和模型分析。实验采用振动弦法黏度计对R32(温度范围为263～350 K、压力范围为2～30 MPa)和R32/R1234yf混合物(温度范围263～360 K、压力范围为2～30 MPa、R32摩尔分数分别为0.244 8、0.410 8、0.608 6、0.835 6)的黏度进行了测量。本文共获得177组实验数据，实验数据的不确定度为2%。利用获得的实验数据对R32及R32/R1234yf混合制冷剂黏度模型进行了研究，建立了基于硬球模型的黏度方程。R32黏度实验数据与方程的平均绝对偏差为0.28%，最大绝对偏差为0.92%；R32/R1234yf黏度实验数据与方程的平均绝对偏差为0.69%，最大绝对偏差为2.09%。通过对比可知，本文实验数据与已有文献数据及黏度方程吻合较好，所得黏度方程可用于R32和R32/R1234yf混合制冷剂的应用研究。

[1] MOLINA M J, ROWLAND F S. Stratospheric sink for chlorofluoromethanes: chlorine atom-catalyzed destruction of ozone[J]. Nature, 1974, 249: 810-812.

[2] MCLINDEN M O, KAZAKOV A F, BROWN J S, et al. A thermodynamic analysis of refrigerants: possibilities and tradeoffs for low-GWP refrigerants[J]. International Journal of Refrigeration, 2014, 38: 80-92．

[3] AHRI. Participants′handbook: AHRI low-GWP alternative refrigerants evaluation program (low-GWP AREP)[R]. Arlington: Air-Conditioning, Heating, and Refrigeration Institute, 2015.

[4] SETHI A, BECERRA E V, MOTTA S Y. Low GWP R134a replacements for small refrigeration (plug-in) applications[J]. International Journal of Refrigeration, 2016, 66: 64-72.

[5] 李连生. 制冷剂替代技术研究进展及发展趋势[J]. 制冷学报, 2011, 32(6): 53-58. (LI Liansheng. Research progress on alternative refrigerants and their development trend[J]. Journal of Refrigeration, 2011, 32(6): 53-58.)

[6] 陈光明, 高能, 朴春成. 低碳制冷剂研究及应用最新进展[J]. 制冷学报, 2016, 37(1): 1-11. (CHEN Guangming, GAO Neng, PIAO Chuncheng. State of the art of research and applications of low-carbon refrigerants[J]. Journal of Refrigeration, 2016, 37(1): 1-11.)

[7] MOTA-BABILONI A, NAVARRO-ESBRJ, BARRAGN, et al. Drop-in energy performance evaluation of R1234yf and R1234ze(E) in a vapor compression system as R134a replacements[J]. Applied Thermal Engineering, 2014, 71(1): 259-265.

[8] HODNEBROG Ø, ETMINAN M, FUGLESTVEDT J S, et al. Global warming potentials and radiative efficiencies of halocarbons and related compounds: a comprehensive review[J]. Reviews of Geophysics, 2013, 51(2): 300-378.

[9] AKASAKA R. Thermodynamic property models for the difluoromethane (R-32) + trans-1,3,3,3-tetrafluoropropene (R-1234ze(E)) and difluoromethane + 2,3,3,3-tetrafluoropropene (R-1234yf) mixtures[J]. Fluid Phase Equilibria, 2013, 358: 98-104.

[10] GELLER V Z, PAULAITIS M E, BIVENS D B, et al. Viscosities of HFC-32 and HFC-32/lubricant mixtures[J]. International Journal of Thermophysics, 1996, 17(1): 75-83.

[11] ASSAEL M J, DYMOND J H, POLIMATIDOU S K. Measurements of the viscosity of R134a and R32 in the temperature range 270-340 K at pressures up to 20 MPa[J]. International Journal of Thermophysics, 1994, 15(4): 591-601.

[12] ASSAEL M J, KARAGIANNIDIS L, POLIMATIDOU S K. Measurements of the viscosity of new refrigerants in the temperature range 270-340 K at pressures up to 20 MPa[J]. International Journal of Thermophysics, 1995, 16(1): 133-143.

[13] RIPPLE D, MATAR O. Viscosity of the saturated liquid phase of six halogenated compounds and three mixtures[J]. Journal of Chemical and Engineering Data, 1993, 38(4): 560-564.

[14] LAESECKE A, LÜDDECKE T O D, HAFER R F, et al. Viscosity measurements of ammonia, R32, and R134a. vapor buoyancy and radial acceleration in capillary viscometers[J]. International Journal of Thermophysics, 1999, 20(2): 401-434.

[15] SUN Liqun, ZHU Mingshan, HAN Lizhong, et al. Viscosity of difluoromethane and pentafluoro-ethane along the saturation line[J]. Journal of Chemical and Engineering Data, 1996, 41(2): 292-296.

[16] OLIVEIRA C M B P, WAKEHAM W A. The viscosity of R32 and R125 at saturation[J]. International Journal of Thermophysics, 1993, 14(6): 1131-1143.

[17] HEIDE R, SCHENK J. Determination of transport quantities of HFC, Vol. 1 Viscosity and surface tension [R] Frankfurt: Research Council for Refrigeration Technology, 1996.

[18] MENG Xianyang, QIU Guosheng, WU Jiangtao, et al. Viscosity measurements for 2,3,3,3-tetrafluoroprop-1-ene (R1234yf) and trans-1,3,3,3-tetrafluoropropene (R1234ze(E))[J]. The Journal of Chemical Thermodynamics, 2013, 63: 24-30.

[19] HUBER M L, ASSAEL M J. Correlations for the viscosity of 2,3,3,3-tetrafluoroprop-1-ene (R1234yf) and trans-1,3,3,3-tetrafluoropropene (R1234ze(E))[J]. International Journal of Refrigeration, 2016, 71: 39-45.

[20] CUI Junwei, BI Shengshan, MENG Xianyang, et al. Surface tension and liquid viscosity of R32 + R1234yf and R32 + R1234ze[J]. Journal of Chemical and Engineering Data, 2016, 61(2): 950-957.

[21] DANG Yagu, KAMIAKA T, DANG Chaobin, et al. Liquid viscosity of low-GWP refrigerant mixtures (R32+R1234yf) and (R125+R1234yf)[J]. The Journal of Chemical Thermodynamics, 2015, 89: 183-188.

[22] DANG Yagu, KIM H S, DANG Chaobin, et al. Measurement of vapor viscosity of R1234yf and its binary mixtures with R32, R125[J]. International Journal of Refrigeration, 2015, 58: 131-136.

[23] TOUGH J T, MCCORMICK W D, DASH J G. Viscosity of liquid he II[J]. Physical Review, 1963, 132(6): 2373-2378.

[24] MENG Xianyang, ZHANG Jianbo, WU Jiangtao. Compressed liquid viscosity of 1,1,1,3,3-pentafluoropropane (R245fa) and 1,1,1,3,3,3-hexafluoropropane (R236fa)[J]. Journal of Chemical and Engineering Data, 2011, 56(12): 4956-4964.

[25] 张建波, 孟现阳, 邱国盛, 等. 高压振动弦黏度测量实验系统的研制[J]. 西安交通大学学报, 2012, 46(11): 30-34. (ZHANG Jianbo, MENG Xianyang, QIU Guosheng, et al. Development of vibrating-wire viscometer for liquid at high pressure[J]. Journal of Xi′an Jiaotong University, 2012, 46(11): 30-34.)

[26] TILLNER-ROTH R, YOKOZEKI A. An international standard equation of state for difluoromethane (R-32) for temperatures from the triple point at 136.34 K to 435 K and pressures up to 70 MPa[J]. Journal of Physical and Chemical Reference Data, 1997, 26(6): 1273-1328.

[27] AKASAKA R. Thermodynamic property models for the difluoromethane (R-32) + trans-1,3,3,3-tetrafluoropropene (R-1234ze (E)) and difluoromethane+ 2,3,3,3-tetrafluoropropene (R-1234yf) mixtures[J]. Fluid Phase Equilibria, 2013, 358: 98-104.

[28] ASSAEL M J, DYMOND J H, PAPADAKI M, et al. Correlation and prediction of dense fluid transport coefficients. I.n-alkanes[J]. International Journal Thermophysics, 1992, 13(2): 269-281.

[29] MILLAT J, DYMOND J H, NIETO de CASTRO C A, et al. Transport properties of fluids: their correlation, prediction and estimation [M]. Cambridge: Cambridge University Press, 1996.