拖曳体激发内波时空特性实验及其理论模型∗

陈科王宏伟盛立尤云祥

1)(上海交通大学,海洋工程国家重点实验室,上海 200240)

2)(高新船舶与深海开发装备协同创新中心,上海 200240)

3)(中国舰船研究设计中心上海分部,上海 201108)

4)(中国人民解放军92537部队,北京 100161)

1 引 言

自20世纪中期,对密度分层流体中运动物体及其尾迹产生的内波问题一直是国内外水动力学及海洋遥感探潜反潜等方面的研究者所感兴趣的[1].从拖曳体产生内波相关速度的角度[2],可以将密度分层流体中拖曳体产生的内波分为两大类:一类是体积效应内波,它是由物体本身排水体积及其尾部跟随拖曳体做定常运动的分离泡共同产生的;另一类是尾迹效应内波,它是由物体尾部湍流尾迹或脱落涡以及混合区的重力塌陷等产生的.

对拖曳体激发内波而言,体积效应内波与尾迹效应内波的转换或占优问题与Froude数Fr=U/(DNmax)密切相关,其中U和D分别是物体运动速度和最大回转直径,Nmax为密度分层流体的最大浮频率.针对球体的实验研究发现[2−7]:当Fr＜Frc=2.0时,体积效应内波占优;而当Fr＞Frc时,尾迹效应内波占优.考虑到实际水下航行体通常是一个细长体,赵先奇等[8]实验研究了长径比λ=L/D=9的拖曳圆柱体,结果表明,临界Froude数Frc不再近似为2.0,而是近似为4.0.王进等[9]以长径比为7的细长回转体(一端为流线型而另一端为钝体型)为对象,研究了头部和尾部形状对转捩后内波波高随拖曳速度的变化规律.同时期,王进等[10]又以3个不同长径比(λ=1,4,9)实验模型为对象进行了实验研究,并结合前述实验结果[8,9],拟合出临界Froude数Frc与长径比λ近似满足线性关系Frc=0.2391λ+1.7579,且转捩后内波波高随拖曳速度线性增大的规律与长径比无关.最近,王宏伟等[11]通过对称布置电导率探头阵列方法,对长径比为7.7的细长回转体(也是一端为流线型而另一端为钝体型)在密度跃层下方5个不同潜深处运动产生内波特性进行了实验研究,结果表明,轴对称细长回转体产生的尾迹效应内波关于物体中纵剖面是不对称的,内波波高随潜深呈指数衰减,并给出了定量表达.

对于定常运动物体产生体积效应内波,理论上可以用定常移动的点源或偶极子来模拟[12−21],其中又以Milder[19]提出的模型最为成熟.在Milder[19]的模型中,其利用二维Fourier变换得到水平波数域上的内波控制方程,结合“刚盖假设”得到上下刚性边界条件,求解内波控制方程对应的特征值问题,结合对应的Green函数,通过卷积和留数定理,得到波数域上位移表达式,最后通过Fourier逆变换得到空间域上的位移场.该方法能估算有限深任意密度分层流体中匀速运动物体生成内波垂向位移场.Robey[2]利用Milder[19]模型进行了数值计算,给出了圆柱体源对称轴长度、直径以及移动速度的方法,并与实验获得的内波波形结构及波高进行了比较,结果符合良好.尤云祥等[20]尝试将圆柱体源改为椭球体源,改进对称轴长度的表达,与Robey[2]实验结果比较,结果也符合很好.

在尾迹效应内波方面,已有很多实验文献报道[2−11,22−26];在理论和数值研究方面,也有学者进行了探索性研究[2,20,26−33].Dupont和Voisin[32]提出移动振荡球形源模型,模拟物体尾部周期性涡泄生成内波问题,与实验结果比较,在内波波系及波形方面,两者符合良好;但是该模型是在浮力频率为常数和无界条件下导出的,对于分层环境和边界适应性较差.Robey[2]利用Milder[19]定常内波模型,将尾流等效为圆柱体模型,结合实验得到的内波相关波速和尾流增长规律,给出了尾流等效圆柱体移动速度、长度和直径的方法,并与实验结果进行了比较,内波波高分布与实验符合良好,但波形结构有些差异.梁川等[33]受尾流周期性涡泄现象启发,提出移动脉动源方法,丰富了内波波形波系的表达,但在波高方面并未做研究.尤云祥等[20]指出,理论和数值的研究结果很难与实验完全符合,在不同方面存在差异,这是由于尾迹激发源成分较为复杂,不仅有周期性涡泄、湍流等随机脉动问题,还包括各种不稳定结构、内波破碎及混合与塌陷等.

需要指出的是,目前有关水下运动物体激发内波特性研究尚有不完善之处.其一,目前的等效源理论模型是针对拖曳球的,而对拖曳细长体产生体积效应内波激发源的参数设置等问题,迄今尚不清楚.其二,王宏伟等[11]的最新实验研究结果表明:轴对称细长回转体在拖曳运动下产生的尾迹效应内波关于物体中纵剖面是不对称的,分解后发现即存在正对称成分又存在反对称成分,而在已有理论模型研究中,移动奇性源(点源、偶极子以及等效质量源等)的设置都是轴对称的,这对于上述实验结果的预测是不合适的.其三,已有细长体模型是圆柱体[8]或只有一端为流线型的回转体[9−11],而实际潜艇头部和尾部应均为流线型,对于此类细长体的实验研究仍未见报道.

有鉴于此,本文在王宏伟等[11]的最新实验研究启发下,同样将电导率探头在整个横剖面内对称布置,对1个球体(直径为10cm)和2个头部和尾部均为流线型的细长回转体(最大回转直径均为10cm而长度分别为50cm和80cm)在拖曳运动下产生内波特性进行了实验研究;同时,本文在尤云祥等[20]针对拖曳球生成内波的等效质量源理论模型的基础上,结合上述3个模型的实验结果,提出了不同长径比模型的体积效应激发源的参数设置方法以及尾迹效应激发源的正对称和反对称等效源的组合设置及其参数设置等具体方法.

2 实验系统及方法

实验在解放军理工大学重力式分层流水槽系统中进行,该系统由水槽主体、分层流制取系统、循环拖曳系统、内波动态测量系统和实验模型等组成,实验系统示意图及相关说明见文献[11],不再赘述.实验模型为1个球体和2个细长回转体,特征直径均为D=10cm,细长回转体模型均由一个长为11cm的流线型头部及一个长为12cm的流线型尾部制作而成,总长度L分别为50和80cm,如图1所示.模型内部中空,用于配重.若将球体看作长径比为1的模型,则两个细长体模型的长径比分别为λ=L/D=5和8.为下文陈述方便,将这3个模型按长径比从小到大依次简称为model A,B和C.采用双线循环拖曳法驱动实验模型,其拖曳方法与文献[11]一致.

图1 两个细长体模型照片(model B,model C)Fig.1.Photograph of two slender bodies(model B,model C).

为下文陈述方便,建立直角坐标系oxyz.水槽长度方向为x轴,宽度方向为y轴,深度方向为z轴,oz轴垂直向下为正,oxz面为水槽中纵剖面.本文实验采用强跃层分层流体.实验中,首先快速注入密度为1000 kg/m3的淡水至厚度为25cm,静置一段时间后,通过水槽底部的两个蘑菇型圆盘进水口缓慢地注入密度为1022 kg/m3的盐水,直到总水深h=80cm.利用电导率探头,采用垂直下降的方式,测量水槽中密度分层流体的密度剖面及浮频率剖面,结果如图2所示.其中,浮频率由下式定义:

式中,g为重力加速度,ρ为密度垂向分布.因z轴向下,故式中省略负号.由图2(a)可知,在本实验分层流体系统中,上层为厚度约20cm的密度均匀层;中间层为厚度约15cm的密度连续分布的过渡层;下层为厚度约45cm的密度均匀层.考虑到密度垂向剖面随实验变化,取实验过程中某次工况下的剖面作为示意图,密度分层流体的最大浮频率在水面下zP=25cm处,并在Nmax=1.86 rad/s附近变化.

图3给出了实验中电导率探头布置示意图,在水槽长度方向不同x轴位置布置两组电导率探头阵列,所有探头的垂向位置均位于z=zP处;第一组阵列沿着水槽宽度y方向对称布置23个电导率探头,用P0,P±1,···,P±11对各探头进行编号,每个探头沿y方向间隔Δy1=5cm,探头P0在水槽横向正中间处.该组电导率探头阵列用来测量模型运动产生内波的时空特征.第二组阵列在沿着水槽宽度y方向对称布置8个电导率探头,其y轴位置分别与第一组的P±2,P±4,P±6和P±8探头对应,将其分别编号为Q±2,Q±4,Q±6和Q±8,各探头沿y方向间隔Δy2=10cm,并与第一组探头在x方向的间距为Δx=146cm.该组探头用来测量分析模型运动产生内波沿ox轴方向传播的相关速度.

图2 (a)密度及(b)浮频率剖面Fig.2.Pro files of(a)density and(b)buoyancy frequency.

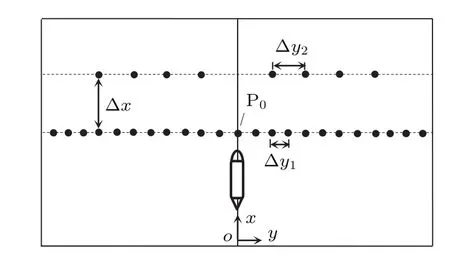
图3 坐标系及探头布置示意图Fig.3.Schematic of the coordinate system and arrangement of probes.

将实验模型置于自由面下d=37cm处,即实验模型中心轴线距离电导率探头为12cm.在每次实验中,电导率探头采样时间均为10 min,然后等待约40 min,再进行下一个工况的实验.实验模型的运动速度范围为,对应的Froude数的范围为,Reynold数的范围为6000.其中,ν为模型回转中心所在深度处背景流体的运动学黏性系数.在每次实验后,最大浮频率的值略有变化.为此,在每次实验前重新测量一次密度剖面,以获得浮频率的最大值,用来计算相应的Froude数Fr.

3 理论模型

对于密度分层流体中拖曳体激发内波问题,无论是拖曳体自身排水体积产生的体积效应内波,还是其尾部湍流尾迹等产生的尾迹效应内波,其激发源都相当于某种体积效应,理论上均可用具有一定移动速度和体积的等效源Q(x,y,z,t)来简化处理.

假设流体是无黏不可压缩的,物体运动激发的内波是小振幅的.将等效源Q加入到连续性方程中,在Boussinesq近似下,可将内波线性化方程简化到随体坐标系中为[2,19,20]

其中Δh为水平Lapalace算子,η为垂向位移,Us为源的移动速度,

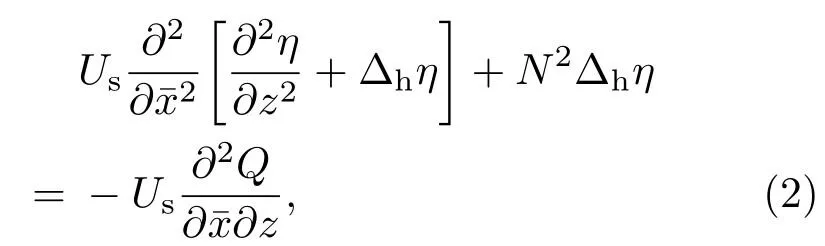
对于内波问题,由于它引起的水面位移很小,可做“刚盖”处理,因此垂向位移满足边界条件η=0(z=0,h).记为η 关于水平变量的二维Fourier变换,水平波数矢量为k,其纵向和横向分量分别为kx和ky,为k的幅值,则(2)式经过二维Fourier变换后为[2,20]

其中ω=kxUs为移动质量源产生内波的频率.

上述定解问题对应的特征值问题为[2,20]

对给定的k,特征值问题(4)有无数个离散的特征值ωm和归一化特征函数ϕm(m=1,2,3,···),每一个离散值对应一个内波模态.在求得特征值ωm(k)后,内波相速度cpm与群速度cgm可以分别表示为[2,20]

为求得内波垂向位移场,需定义Green函数G(z;z0)满足如下方程[2,19]:

特征函数系{ϕm}在[0,h]上是一个完备的正交系,由此可得[2]

再由(3),(6)和(7)式可求得水平波数空间下的垂向位移解为[2,20]

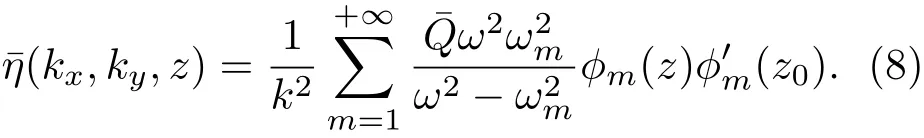
(8)式中,ϕm(z)是观测深度处的特征函数值,其深度与实验中电导率探头所在深度(也即最大浮频率所在深度zP)对应;而是移动源回转中心所在深度的特征函数导数值,其深度与实验模型中心所在深度对应.

对于等效质量源的设置,尤云祥等[20]设计了一个移动速度为Us的椭球体模型,设椭球长轴为2a,椭球回转直径为2b,其在x=Ust+ξ处截面积可表示为[20]

则移动源Q可表示为[20]

实验研究表明[11],体积效应内波关于水槽中纵剖面几乎是对称的,因此用(10)式中与物体几何形状相近的等效源来模拟体积效应内波的激发源是合理的.尤云祥等[20]仅给出了针对拖曳球的参数设置方法,而针对细长体模型,该等效源中的参数如何设计是本文的创新之处.

实验研究还表明[11],尾迹效应内波关于水槽中纵剖面是不对称的,通过奇偶分解法发现其既有对称成分也有反对称成分.为此,对尾迹效应内波激发源,分别设计为关于水槽横剖面y方向一对正对称的激发源组合和一对反对称的激发源组合,如图4所示.具体表达式如下:

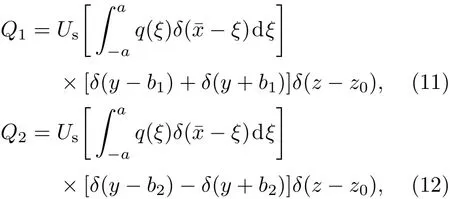
其中Q1为一对正对称的激发源组合,Q2为一对反对称的激发源组合.这里仍借用椭球体源,即,S(ξ)的表达式同(9)式是一致的,只是回转半径b分别用b1和b2代替.比较(10)—(12)式可知,正对称等效源组合相当于将回转半径为b1的等效源分别沿y轴正负方向平移b1个单位后再相加组合而成,相当于y方向两个对称源叠加;而反对称等效源组合相当于将回转半径为b2的等效源分别沿y轴正负方向平移b2个单位后再相减组合而成,相当于y方向源汇叠加.

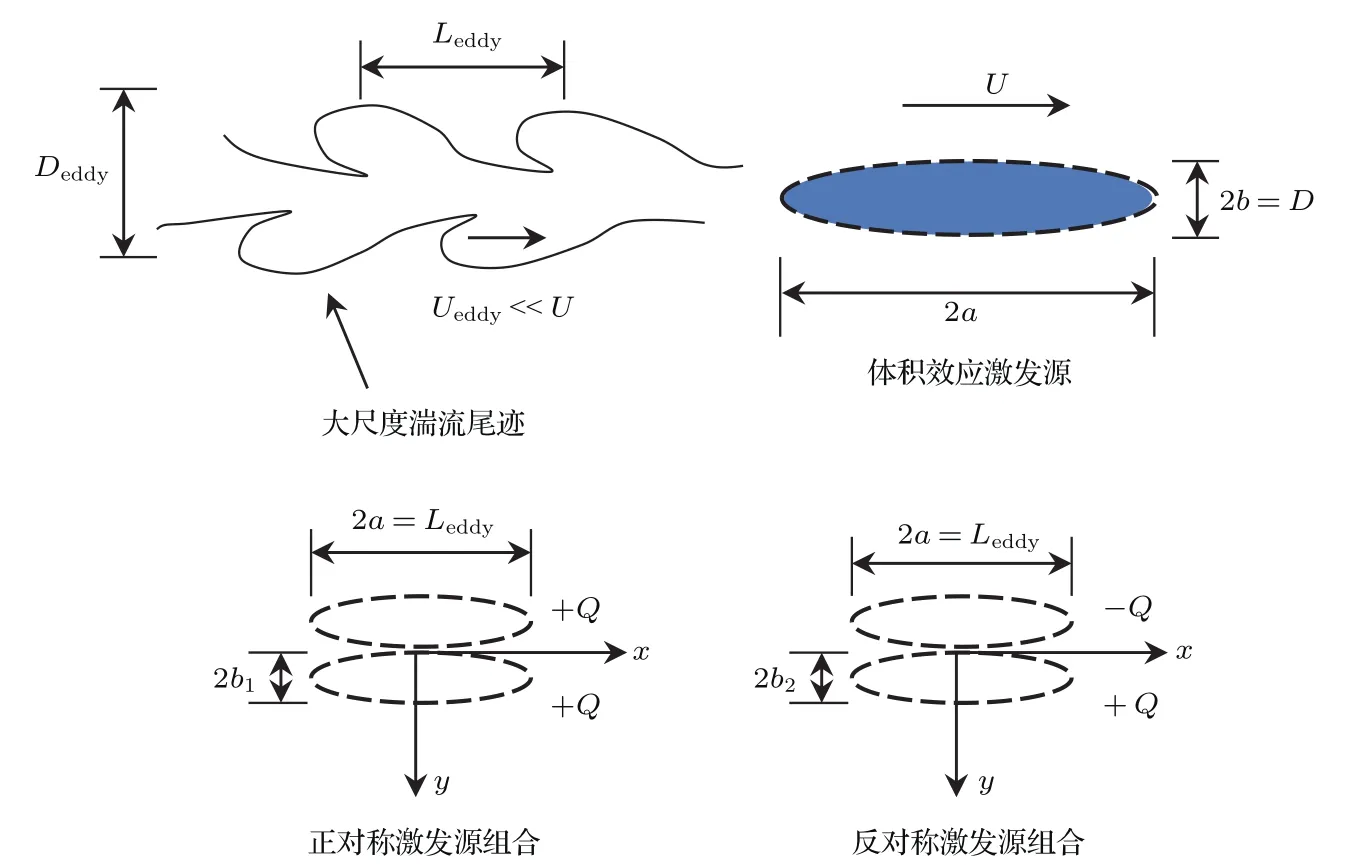
图4 拖曳细长体的体积效应和尾迹效应激发源示意图Fig.4.Schematic of the body-effect and wake-effect sources for towed slender body.

对于(8)式,逆变换只能在一个维度上有理论解,而另一个维度需要数值计算.已有理论[2,19,20]通常将kx做Fourier逆变换回x¯,并利用留数定理得到

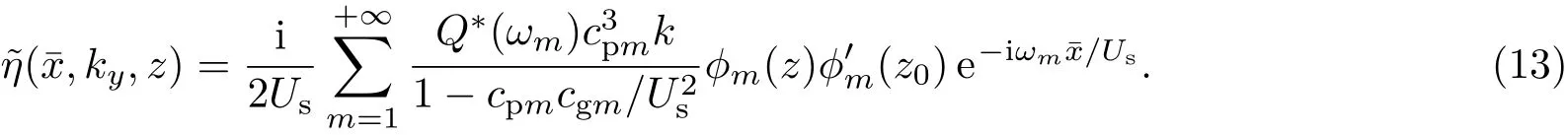
对于体积效应等效源,选择(10)式,则(13)式的具体形式为[20]

对于尾迹效应等效源,选择正对称组合源时,则(13)式的具体形式为

当选择反对称组合源时,则(13)式的具体形式为

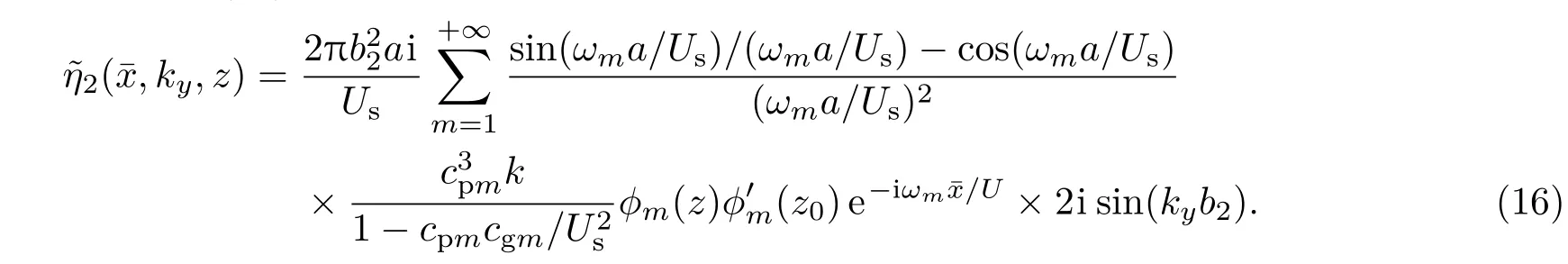
比较(14)—(16)式可得,正对称组合源所得结果表达式(15)比体积效应激发源所得结果表达式(14)多出了2cos(kyb1)乘积因子,而反对称组合源所得结果表达式(16)比(14)式多出了2i sin(kyb2)乘积因子.而等效源的移动速度和尺寸的确定依赖于实验结果,将在下一节中详细阐述.

4 实验结果与分析

本节重点研究不同长径比模型在拖曳下运动产生两类内波的转捩特性,转捩前后两类内波的波高变化规律和位移场特性以及转捩前后两类内波的时空特征及其对称性等问题,为理论模型提供先验参数.

4.1 内波相关速度

关于内波速度的说法较多,包括内波波致流速、线性相速度和非线性相速度等[34],也包括前文提到的相速度和群速度等,但本节的内波相关速度与上述速度有所不同,它只是用来表征内波相对于运动物体是否定常.本节参照Robey[2]对于内波相关速度的测量方法,设P和Q是位于水槽同一纵剖面上前后布置的两个电导率探头,探头位于水下同一个深度,两个探头之间的纵向距离为Δx.对各探头测到的密度扰动时历进行相关性分析,记Δt为相关性峰值对应的时间,此即内波从起始探头P传播到另一个探头Q所需的时间,定义内波相关速度为Uiw=Δx/Δt.

在图5中,给出了3个模型生成内波相关速度Uiw随拖曳速度U变化特性的实验结果,其中虚线表示Uiw=U.由图5可知:存在一个临界拖曳速度Uc(竖线所示),当U＜Uc时,在水槽不同纵剖面上,内波相关速度均与实验模型的拖曳速度一致,表明模型拖曳扰动产生内波相对模型的运动是定常的;当U＞Uc时,在水槽不同纵剖面上,内波相关速度均出现突然下降的现象,而且要远小于模型的拖曳速度,表明此时模型拖曳扰动产生内波相对模型的运动是非定常的.进一步观察发现,3个模型的临界速度不同,分别为Uc=36,50和60cm/s.

对拖曳球扰动产生内波的转捩特性问题,Robey[2]利用具有强跃层的温度分层水槽,针对直径D=10cm的球体,得到临界Froude数Frc=Uc/(DNmax)≈2.0.王进等[9,10]利用具有强跃层的密度分层水槽,进一步研究了回转直径D=7cm的4个不同长径比(λ=1,4,7和9)的轴对称回转拖曳体产生内波的转捩特性问题,发现Frc与长径比λ之间存在线性增长关系Frc=0.2391λ+1.7579.

图5 内波相关速度Uiw随拖曳速度U的变化(a)model A;(b)model B;(c)model CFig.5.Internal wave correlation velocity Uiwversus towing speed U:(a)model A;(b)model B;(c)model C.

本文实验模型回转直径为D=10cm,最大浮力频率随着实验进行会逐渐减小,大致范围为Nmax≈2.0—1.6,由平均密度剖面得到的最大浮力频率Nmax≈1.86 rad/s.将上述3个临界速度无量化,得到Frc≈1.94,2.69,3.23,经过线性拟合得到

本文结果同样表明,长径比对两类内波之间的转捩特性有明显影响,长径比越大,临界Froude数Frc越大.但本文拟合得到的Frc与λ的线性关系与王进等[9,10]得到的线性关系略有不同,本文斜率略偏小.注意到本文细长回转体模型头部和尾部均为流线型,而王进等[9,10]的细长回转体模型只有头部为流线型.所以本文细长体模型有效长度其实小于总长,这使得体积效应内波向尾迹效应内波转捩的临界Froude数Frc偏小.再者,本文细长回转体的回转直径大于王进等[9,10]细长回转体的回转直径,在同样尺度的水槽下,本文模型产生内波受到水槽边壁和底部等反射的影响比王进等[9,10]要大.虽然两者线性关系存在略微差异,但两者对Frc随长径比λ增大而线性增大这一规律的预测是一致的.

进一步观察发现,转捩后,3个模型的内波相关速度Uiw均在8—22cm/s之间的一个条带内,无量纲化得到Friw=Uiw/(DNmax)=0.43—1.18.结果表明,转捩后长径比对尾迹效应内波相关速度的影响很小.

4.2 内波波高

对内波波高的统计方法,在文献[2,7—10]中,主要采用某个传感器处内波位移时历的峰-峰幅值作为波高,但这一峰-峰幅值究竟是相邻峰-峰幅值最大值,还是最大峰与最大谷的差值,并没有给出明确的说法.且文献[2,7—10]只选取某个探头处的峰-峰值作为该速度下的波高,而未考虑空间上其他探头处的波高,因此有一定局限性.

本文对第一组23个探头采集到的密度扰动信号取其前100 s的时间序列,将采集到的密度扰动信号换算为相应的内波位移信号,分别取最大峰与最大谷的差值作为该探头的波高H(y),得到无量纲波高H(y)/H0在横剖面上的分布,如图6所示,其中H0=H(0),为中间探头y=0处的波高,图中实线为B=0.2 m的如下高斯函数

高斯分布是正态分布的别称,其半宽值B相当于正态分布中的标准差,可以为下文平均波高的统计提供理论依据.由图6可知:在−0.25 m ＜y＜0.25 m范围内,在不同长径比下,H(y)/H0随y变化的散点图近似与高斯分布一致;但在−0.25 m＜y＜0.25 m范围外,H(y)/H0随y变化的散点图与高斯分布偏离很大,这主要与水槽侧壁导致的内波反射有关.由此可见,在前100 s的时间内,拖曳模型产生内波在−0.25 m＜y＜0.25 m范围内,受水槽侧壁的影响较小.为此,采用如下方法统计内波波高:在−0.25 m＜y＜0.25 m范围内,对9个电导率探头P0,P±1,P±2,P±3和P±4所得内波位移时历的最大峰-峰幅值进行统计,取其平均值为内波波高,记为Hm.

图6 转捩前波高H(y)/H0随y轴分布(a)model A;(b)model B;(c)model CFig.6.Distribution of wave height H(y)/H0along y-axis before transition:(a)model A;(b)model B;(c)model C.

图7给出了3个模型产生内波波高Hm随拖曳速度U的变化规律的实验结果.由图7可知,对不同长径比模型,在各自转捩速度前,内波波高随拖曳速度变化规律均为先增大后减小,而在各自转捩速度后,内波波高随拖曳速度增大而近似线性增大.记转捩前波高峰值对应速度为Up,则3个模型的Up分别为10,14和18cm/s,无量纲化得到Frp=Up/(DNmax)=0.54,0.75和0.97.关于Lee波波高(波幅)随拖曳Fr的变化规律,已有实验研究[2,5,8−11]均得到先增大后减小这一规律.对于拖曳球,Chomaz等[5]在盐分层流体中得到Lee波峰值对应Frp=0.5—0.6;Robey[2]在温度分层流体中得到Frp=0.7—0.8;本文拖曳球Frp=0.54,与文献[2,5]实验结果基本一致,说明这些规律是普适的.细微的差异可能跟密度剖面等的测量误差导致Nmax变化较大有关.王进等[9,10]对回转直径D=7cm的4个不同长径比(λ=1,4,7,9)的轴对称回转拖曳体的实验研究发现,细长体的波高随Fr的变化规律同球体相似,也是先增大后减小,Lee波峰值对应Frp与长径比λ之间也存在线性增长关系Frp=0.0957λ+0.7254.本文结果同样是Frp随λ增大而增大,经过线性拟合可得

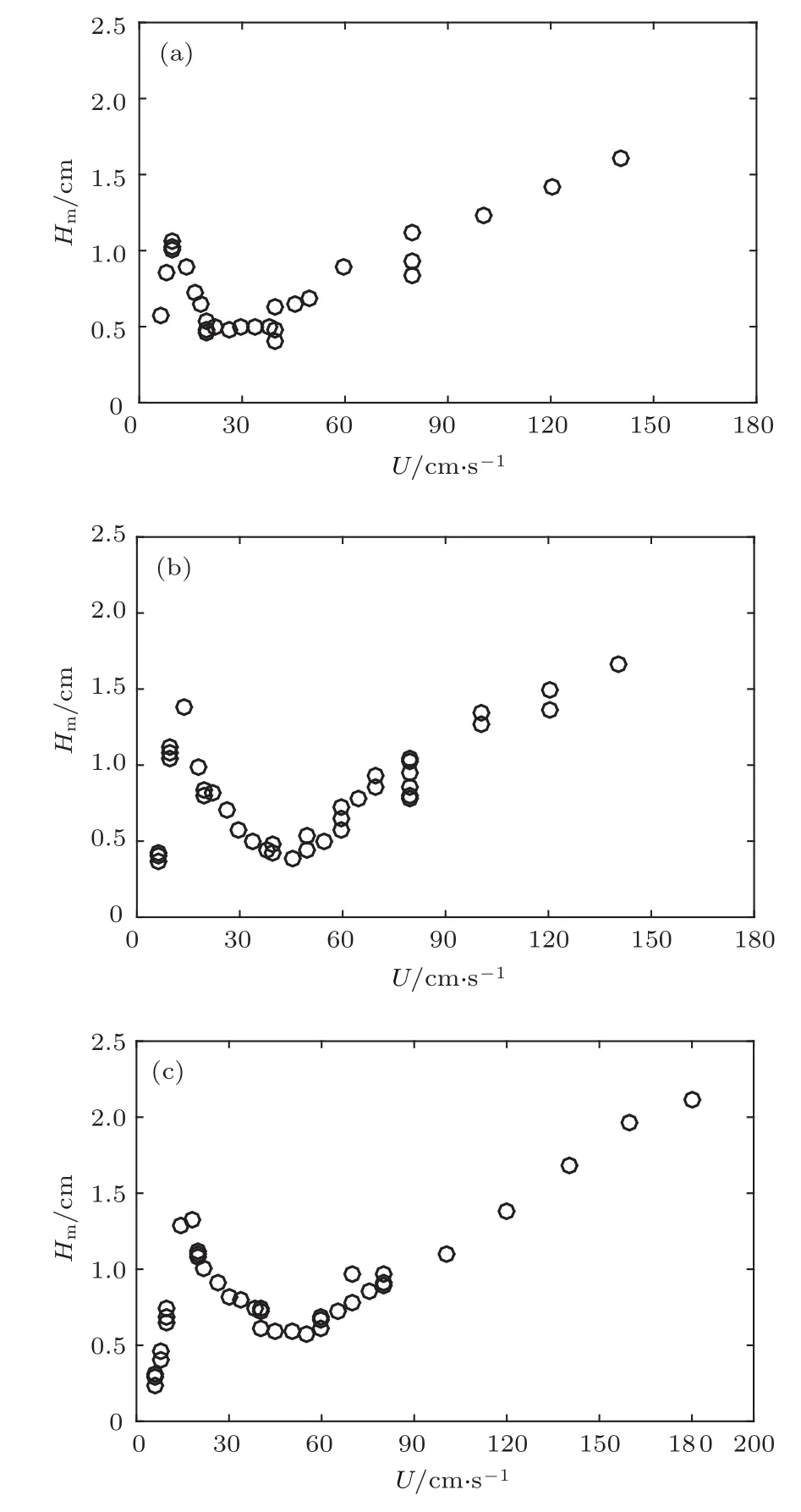
图7 内波波高Hm随U的变化(a)model A;(b)model B;(c)model CFig.7.Internal wave height Hmversus U:(a)model A;(b)model B;(c)model C.

本文结果同样表明,长径比对Lee波峰值对应Froude数Frp有明显影响.但本文拟合得到的Frp与λ的线性关系与王进等[9,10]得到的线性关系略有不同,本文斜率略偏小.原因同上一节转捩点随长径比变化规律的解释相同,仍然是有效长度不同而导致的差异.进一步观察还可以发现,转捩后,3个模型内波波高随拖曳速度增大而近似线性增大,且线性增大的斜率几乎一致.这意味着,转捩后长径比对尾迹效应内波波高的影响很小.

4.3 内波时空形态特征

为下文陈述方便,首先介绍移动源致内波的等相线理论[13].记(cpm)0为第m模态的内波临界相速度,当内波激发源移动速度Us＞(cpm)0时,该模态内波只有散波;当Us＜(cpm)0时,该模态内波既有散波又有横波.在本文实验所获密度分层流体的浮频率剖面下,经计算可得前两个模态的临界相速度分别为18.1cm/s和3.7cm/s.本文实验中拖曳速度的范围为6—160cm/s,该速度范围均大于第二模态及更高阶模态内波的临界相速度.因此,在本文实验工况下,二阶及更高阶模态内波只有散波.

在图8中,给出了model B在不同速度下运动产生内波时空形态特征的实验结果.其中,前6个速度为转捩前的情况,后4个速度为转捩后的情况,Lee波峰值对应速度Up=14cm/s,临界速度Uc=50cm/s.此外,图中横坐标为水槽宽带方向,范围为[−0.55,0.55](单位为m),纵坐标为时间,范围为[0,120](单位为s).

首先分析转捩前的内波时空形态特征.当U=6,8,10cm/s时,可以观察到两个模态的波系,其中外层波系为第二模态内波,由于U＞(cp2)0,因此只有散波,且张角变化较小;内层波系为第一模态内波,由于U＜(cp1)0,因此既有散波也有横波,且散波张角随速度的增大而增大.当U=14cm/s时,第二模态内波很弱,主要为第一模态内波,由于此时U仍小于(cp1)0,第一模态内波既有散波也有横波.当U=20,34cm/s时,由于U＞(cp1)0,因此第一模态内波只有散波,而且其张角随U的增大变化较小.

在转捩后,实验模型的速度均大于(cp1)0.根据等相线理论[13],此时内波将只有散波而没有横波.但由图8(g)—(j)可见,转捩后的内波既有散波又有横波,而且随着拖曳速度的增大,其空间形态特征变化较小.进一步观察图8(e)—(f),可以发现:在转捩前内波时空形态特征图中,也存在这种既有横波又有散波且空间形态特征变化较小的内波,而且随着拖曳速度的增大,其影响逐渐显著.由此可见,转捩后尾迹效应内波为主控内波,其主要特征表现为:既有横波又有散波,而且内波时空形态特征相似.同时,在转捩前,虽然体积效应内波为主控内波,但在拖曳速度较大时,尾迹效应内波也是存在的.由图8还可发现,转捩前,体积效应内波关于水槽中纵剖面是对称的;转捩后,尾迹效应内波关于中纵剖面是不对称的.

图8 model B在不同速度下的内波时空波形结构Fig.8.Time-space internal wave patterns at different towing speeds for model B.

5 理论计算与实验结果比较

体积效应内波的产生机制可归结为物体本身及其回流区产生的排水效应,由于这两类激发源均跟随物体一起运动,因此体积效应内波相对于物体的运动是定常的.尾迹效应内波的产生机制较为复杂,包括湍流涡激发的随机内波,尾迹塌陷产生的内波以及晚尾迹扰动产生的内波等.本文实验结果表明:当Fr＜Frc时,体积效应内波为主控内波;当Fr＞Frc时,体积效应内波会迅速衰减直至消失,此时尾迹效应内波会取代体积效应内波而成为主控内波.而且尾迹效应激发源并不跟随物体一起运动,其运动速度要远小于模型的拖曳速度,其密度扰动具有时空随机性.在利用(14)—(16)式计算运动物体的激发内波垂向位移场时,移动源的速度Us、回转直径2b(或2b1与2b2)、长度2a等是关键参数.本节尝试利用上一节实验结果,分别对转捩前的体积效应内波激发源和转捩后的尾迹效应内波激发源的参数设置给出具体确定方法,并与实验结果进行比较分析.

5.1 转捩前比较

首先确定转捩前的等效源参数.已有研究[2,20]和本文实验结果均表明:转捩前,内波相关速度Uiw等于物体拖曳速度U,内波的运动相对于拖曳体是定常的,因此移动源的速度Us可取为Us=U,这时内波的激发源就是物体的体积效应.

等效源的几何尺寸与运动物体尺寸及其尾部流场是相关的.针对拖曳球的实验结果,Robey[2]设计了一个圆柱体形等效源,转捩前,取移动源回转直径2b=D(球直径)与长度2a=3D这两个几何尺寸,后者所得计算结果与实验结果符合更好.尤云祥等[20]改进移动源的表达,转捩前,仍取移动源的回转直径2b=D,但将长度取为2a=c(2Fr)nD,其中,常数c和n取三组不同组合,得到计算结果更加符合Robey实验结果.目前对细长体激发体积效应内波的激发源的尺寸设置未见报道.考虑到拖曳体尾部仍有一定长度的跟随物体一起定常移动的分离泡,为简化处理,将分离泡的长度取为2D,因此,本文对细长体的体积效应内波激发源的尺寸设置如下:

图9即为转捩前利用本文(14)式的椭球回转体模型和(20)式中等效源的尺寸参数获得的内波垂向波高计算结果与实验结果比较图,同时给出了等效源的长度恰为拖曳体长度的计算结果.由图9可知,对于model A,无论从波高值上,还是Lee波峰值对应速度Up的预报上,a/b=3的计算结果比a/b=1的计算结果与实验结果的符合程度更高.这意味着,拖曳球的体积效应不仅包含其体积本身,还包含跟随它一起做固定移动的分离泡,与已有的研究结果相一致[2].对于本文中研究的细长体,根据理论模型,以a/b=5和a/b=8的假设所得结果分别与model B和model C的实验结果符合程度更高,即细长体的等效源长度恰好与其本身长度相等,并不需要在模型中考虑分离泡的作用.对这种现象的一个合理的解释是:本研究中的细长体头部和尾部均为流线型,其尾流中分离泡的作用区域和强度都要小于球体的尾流,故在设定模型参数时,并不需要额外增加长度.

综上所述,对拖曳球的体积效应的模拟,等效源的尺寸取为a/b=3比a/b=1更为合理;对本文具有流线型头部和尾部的细长体模型的体积效应的模拟,等效源的尺寸取为a/b=λ更为合理.

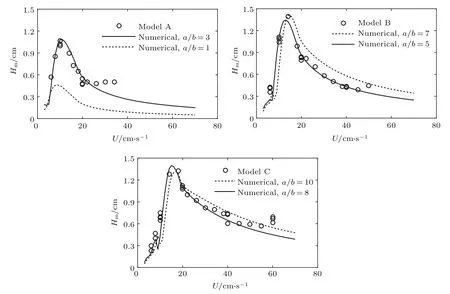
图9 转捩前实验与计算所得内波波高比较Fig.9.Comparison of experimental and numerical internal wave height before the transition.

下面比较分析移动源产生内波波形结构与波系分布等特征.图10给出了model A在转捩前6个速度下,由(14)式计算获得的内波垂向位移的波形结构图,同时给出了实验结果.其中,计算波形图为前三个模态的计算结果.图中横坐标和纵坐标的说明与图8一致.由图10可知,从波形结构和波系分布角度,两者符合都很好.计算结果没有边壁反射,比实验波形结构图更加清晰.当U=6,8,10cm/s时,可以明显地观察到两个模态的波系,其中外层为第二模态的波,由于U＞(cp2)0,因此只有散波;内层为第一模态的波,由于U＜(cp1)0,因此既有散波也有横波.当U=14,18cm/s时,第二模态内波逐渐减弱,当U=18cm/s时,第二模态内波几乎不可见;随着拖曳速度的增大,第一模态内波张角逐渐增大,由于此时U仍小于(cp1)0,因此既有散波也有横波.当U=20cm/s时,由于U＞(cp1)0,因此只有散波,而实验波形图中间隐约出现一类张角较小的波系,该波系既有横波也有散波,这一波系在计算波形图中没有体现,这是尾迹效应内波逐渐显现所造成的.但从相关波速上看,仍然以体积效应内波为主,这也说明了图9中理论模型预测结果与实验结果符合很好但稍有差异的原因.其他两个细长体模型的比较规律类似,鉴于篇幅,不再赘述.

图10 model A转捩前实验与计算所得波形图比较Fig.10.Comparison of experimental and numerical internal wave pattern before the transition for model A.

为进一步比较计算与实验的符合程度,从图10中取出y=−0.2 m处的位移波动的时历进行比较,如图11所示,仅取前100 s的时历进行分析.由图11可知:当速度较小时,计算所得位移波动时历在周期、相位和振幅上与实验结果都符合很好,尤其是前5个周期内;当速度增大至U=18cm/s时,两者在一段时间后出现差异,计算结果在约5个波动周期后趋于平静,而实验结果在整个时间历程都存在波动,这是实验模型尾部逐渐出现的尾迹效应内波所引起的.理论上,在(cp1)0＜U＜Uc时,计算波形图中没有横波,而实验波形图中出现横波,这是两者在波形图上产生差异的本质.尽管如此,从波高的量值及变化趋势上,如图9所示,计算结果与实验结果符合很好.这意味着,转捩前,本文理论模型及其参数设置在波高及其变化趋势预测上是合理的,在波形预测上也是大致符合的.

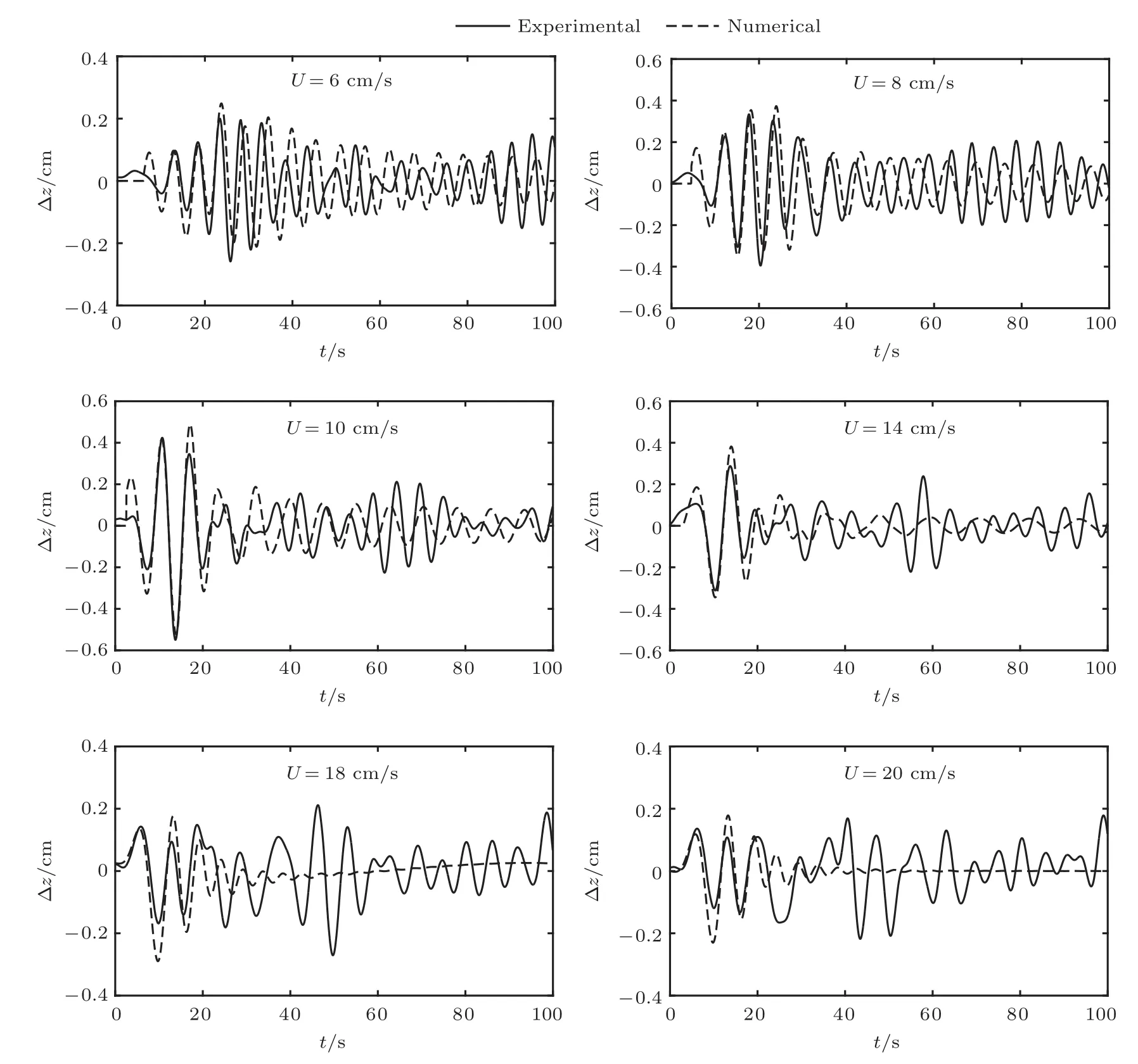
图11 model A转捩前在y=−0.2 m处实验和计算所得位移时历比较Fig.11.Comparison of experimental and numerical time series at y=−0.2 m before the transition for model A.

5.2 转捩后比较

其次确定转捩后的等效源参数.已有研究[2−11]和本文实验结果均表明:转捩后,内波相关速度Uiw小于物体拖曳速度U,内波的运动相对于拖曳体是非定常的.因此移动源的速度Us可取为Us=Uiw,这时内波的激发源就是物体的尾迹效应.

尾迹效应内波激发源的尺寸与拖曳体尾迹中一类大尺度湍流相干涡结构相关.由文献[5,6]可知,水下拖曳体尾迹中主控涡的Strouhal数St=fD/U=0.16—0.2,其中,f为主控涡的频率.如果取St=0.16,那么可得主控涡的流向长度近似为,激励频率近似为,其中为主控涡移动速度.由文献[11]和本文实验结果可知,转捩后内波相关速度Froude数Friw在一个条带内变化,条带均值约为1.0.为此,将Friw近似取为1.0,转捩后内波相关速度近似为.将主控涡移动速度取为内波相关速度,即Ueddy=Uiw,那么可得f≈Nmax/(2π),这正好近似为密度分层流体最大浮频率.Robey[2]取,则主控涡的流向长度近似为,转捩后内波相关速度近似为0.8DNmax,将主控涡移动速度取为内波相关速度,仍可得f≈Nmax/(2π).

对移动源的回转直径,可用湍流尾迹增长公式进行估算[2]

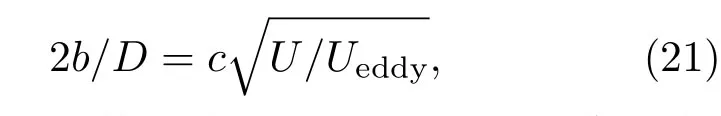
其中c为待定常数.在Robey[2]圆柱体模型中,c=0.25;在尤云祥等[20]回转椭球体模型中,c=0.4.两者所使用的理论模型有所差异,因此系数有所差异,可见常数c是一个需要与实验比较而确定的常数.而且在本文尾迹效应激发源理论模型中,既有正对称组合源,也有反对称组合源,因此与已有理论模型[2,20]是有区别的.这里,c1对应b1,反映正对称组合源回转直径待定系数;c2对应b2,反映反对称组合源回转直径待定系数.

对图8中波形图存在非对称性这一现象,可通过对称位置处时历的和平均或差平均来获取正对称部分和反对称部分的信号.为此,将Δz分解为关于y的偶函数和奇函数两个成分:

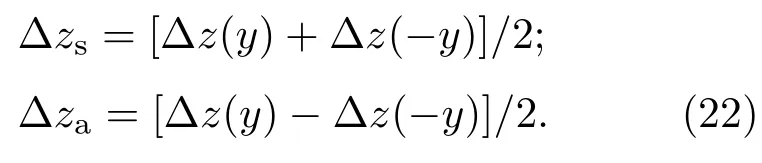
(22)式中,Δzs关于y为偶函数,该函数描述关于水槽中纵剖面对称的内波成分;Δza关于y为奇函数,该函数描述关于水槽中纵剖面反对称的内波成分.

图12给出了利用本文(15)式的正对称源组合和(16)式的反对称源组合模型获得的拖曳体产生内波的垂向波高计算结果,同时给出了利用(22)式分解后的实验结果.所有计算中,移动源的速度Us=10cm/s(在转捩后相关速度范围内),移动源的长度2a=5D.而对于移动源的回转直径2b的设置,根据(21)式,正对称激发源中待定系数c1均为0.22;反对称激发源中待定系数c2分别为0.32,0.29和0.29.由图12可知,无论是正对称的波高还是反对称的波高,计算结果从趋势预测上与实验结果符合较好.对同一个实验模型,系数c1＜c2,但正对称的计算结果大于反对称的计算结果,这正是(15)和(16)式中的激发源分别多出了2cos(kyb1)和2i sin(kyb2)乘积因子造成的结果.由此表明,从波高预测上,上述正反对称源的组合设计是合理的.对于正对称的计算结果与实验结果的比较,3个实验模型的系数相同,这进一步说明长径比对正对称的尾迹效应内波波高的影响很小.而对于反对称的比较结果,细长体的系数略小于球体的,说明流线型的头部和尾部结构使得细长体尾迹产生的反对称内波成分略小于球体尾迹产生的反对称内波成分.

下面比较分析移动源产生内波波形结构与波系分布等特征.以model C为例,图13分别给出了当U=60,80cm/s时,由上述正对称和反对称激发源组合计算获得的内波正反对称波形图,同时给出了由(22)式分解所得的正反对称实验波形图.其中,正对称计算波形图中叠加了Us=U的体积效应内波.由图13可知,转捩后实验波形图中主要存在两类V形波系,其中外层张角较大的V形波系相对于水槽中纵剖面是对称的,这是体积效应内波的成分;内层张角较小的V形波系既有正对称成分,也有反对称成分,这是移动速度较慢的尾迹效应内波.正对称源的计算波形图在波形和波系上与实验结果符合很好,但反对称源的计算波形图与实验结果有些差异,但从图12波高的预测上来看,反对称等效源的设置仍然是合理的.

从图13实验结果还可进一步发现:转捩后尾迹效应内波还会出现塌陷现象.但计算结果中并没有反映出这一塌陷内波.实际上,运动物体激发内波成分是复杂的,尤其是转捩后尾迹效应内波的激发源更是无法归结为哪一类激发源,既有大尺度湍流尾迹产生内波,也有混合区塌陷产生内波,且在有限尺寸的水槽内,水槽边壁导致的内波反射叠加,使得某些内波波系或增强或减弱,这也是理论计算无法预测的.

图13 model C转捩后实验与计算所得波形图比较Fig.13.Comparison of experimental and numerical internal wave pattern after the transition for model C.

6 结 论

在具有密度跃层的分层流体中,采用沿水槽中纵剖面对称布置电导率探头阵列的方法,对1个球体和2个不同长径比流线型细长体在拖曳运动下激发内波时空特性进行了系列实验.结果表明:存在一个与长径比为线性关系的临界Froude数Frc,当Fr＜Frc时,拖曳体产生的内波相对于拖曳模型是定常的,这种内波称为体积效应内波(Lee波);Fr＞Frc时,拖曳体产生的内波相对于拖曳模型是非定常的,且内波波形中既有正对称成分也有反对称成分,这种内波称为尾迹效应内波.

根据实验结果,从内波激发源的角度,采用在线性化质量方程中添加一个具有一定移动速度和体积的等效源的方法,结合内波垂向位移特征值问题,利用Fourier变换,建立了计算不同长径比拖曳体生成内波垂向位移场的一种理论模型.

针对不同长径比拖曳体生成体积效应内波,提出了计算移动源速度、回转直径和长度的方法;针对尾迹效应内波中既有正对称也有反对称这一特性,提出了正对称和反对称的等效源组合方法及其相应的参数设置方法.利用上述方法获得的内波波高、波形结构和波系分布等计算结果,与实验结果均符合良好,表明所建立的理论模型及其参数设置是合理的和有效的.

实际潜艇通常是靠螺旋桨等推进装置运动的,这时如何来确定两类内波的转捩特性,并如何设计移动源及参数设置等问题,将在后续研究中做进一步探索性研究.

[1]Liang J J,Du T,Huang W G,Zeng K,He M X 2016 J.Ship Mech.20 635(in Chinese)[梁建军,杜涛,黄韦艮,曾侃,贺明霞2016船舶力学20 635]

[2]Robey H F 1997 Phys.Fluids 9 3353

[3]Hop finger E J,Flor J B,Chomaz J M,Bonneton P 1991 Exp.Fluids 11 255

[4]Lin Q,Boyer D L,Fernando H J S 1993 Exp.Fluids 15 147

[5]Chomaz J M,Bonneton P,Hop finger E J 1993 J.Fluid Mech.254 1

[6]Bonneton P,Chomaz J M,Hop finger E J 1993 J.Fluid Mech.254 23

[7]Wei G,Zhao X Q,Su X B,You Y X 2009 Sci.China:Series G 39 1338(in Chinese)[魏岗,赵先奇,苏晓冰,尤云祥2009中国科学G 39 1338]

[8]Zhao X Q,You Y X,Chen K,Hu T Q,Wei G 2009 J.Shanghai Jiao Tong Univ.43 1298(in Chinese)[赵先奇,尤云祥,陈科,胡天群,魏岗2009上海交通大学学报43 1298]

[9]Wang J,You Y X,Hu T Q,Wang X Q,Zhu M H 2012 Acta Phys.Sin.61 074701(in Chinese)[王进,尤云祥,胡天群,王小青,朱敏慧2012物理学报61 074701]

[10]Wang J,You Y X,Hu T Q,Zhu M H,Wang X Q,Wei G 2012 Chin.Sci.Bull.57 606(in Chinese)[王进,尤云祥,胡天群,朱敏慧,王小青,魏岗2012科学通报57 606]

[11]Wang H W,Chen K,You Y X,Zhang X S 2017 Chin.Sci.Bull.62 2132(in Chinese)[王宏伟,陈科,尤云祥,张新曙2017科学通报62 2132]

[12]Lighthill J 1978 Waves in Fluid(Cambridge:Cambridge University Press)pp23–30

[13]Keller J B,Munk W H 1970 Phys.Fluids 13 1425

[14]Miles J W 1971 Geo.Fluid Dynamics 2 63

[15]Gray E P 1983 Phys.Fluids 26 2919

[16]Voisin B 1994 J.Fluid Mech.261 333

[17]Yeung R W,Nguyen T C 1999 J.Eng.Math.35 85

[18]Broutman D,Rottman J,Eckermann S D 2004 Annu.Rev.Fluid Mech.36 233

[19]Milder M 1974 Internal Waves Radiated by a Moving Source Technical Report(Vol.1)(Santa Monica:Defense Advanced Research Projects Agency)pp19–25

[20]You Y X,Zhao X Q,Chen K,Wei G 2009 Acta Phys.Sin.58 6750(in Chinese)[尤云祥,赵先奇,陈科,魏岗2009物理学报58 6750]

[21]Brandt A,Rottier J R 2015 J.Fluid Mech.769 103

[22]Lin J T,Pao Y H 1979 Annu.Rev.Fluid Mech.11 317

[23]Gilreath H E,Brandt A 1985 AIAA J.23 693

[24]Wei G,Wu N,Xu X H,Su X B,You Y X 2011 Acta Phys.Sin.60 044704(in Chinese)[魏岗,吴宁,徐小辉,苏晓冰,尤云祥2011物理学报60 044704]

[25]Dupont P,Kadri Y,Chomaz J M 2001 Phys.Fluids 13 3223

[26]Druzhinin O A,Papko V V,Sergeev D A,Troitskaya Y I 2006 Izv.Atmos.Ocean.Phys.42 615

[27]Druzhinin O A 2009 Fluid Dyn.44 213

[28]Vasholz D P 2011 Theoretical and Computational Fluid Dynamics 25 357

[29]Diamessis P J,Gurka R,Liberzon A 2010 Phys.Fluids 22 086601

[30]Abdilghanie A M,Diamessis P J 2013 J.Fluid Mech.720 104

[31]Yao Z C,Zhao F,Liang C,Hong F W,Zhang J 2017 J.Ship Mech.21 8(in Chinese)[姚志崇,赵峰,梁川,洪方文,张军2017船舶力学21 8]

[32]Dupont P,Voisin B 1996 Dynamics Atmo.Oceans 23 289

[33]Liang C,Hong F W,Yao Z C 2015 J.Hydrodynamics Ser.A 30 9(in Chinese)[梁川,洪方文,姚志崇 2015水动力学研究与进展30 9]

[34]Cai S,Xie J,Xu J,Wang D,Chen Z,Deng X,Long X 2014 Deep Sea Res.Part I 84 73